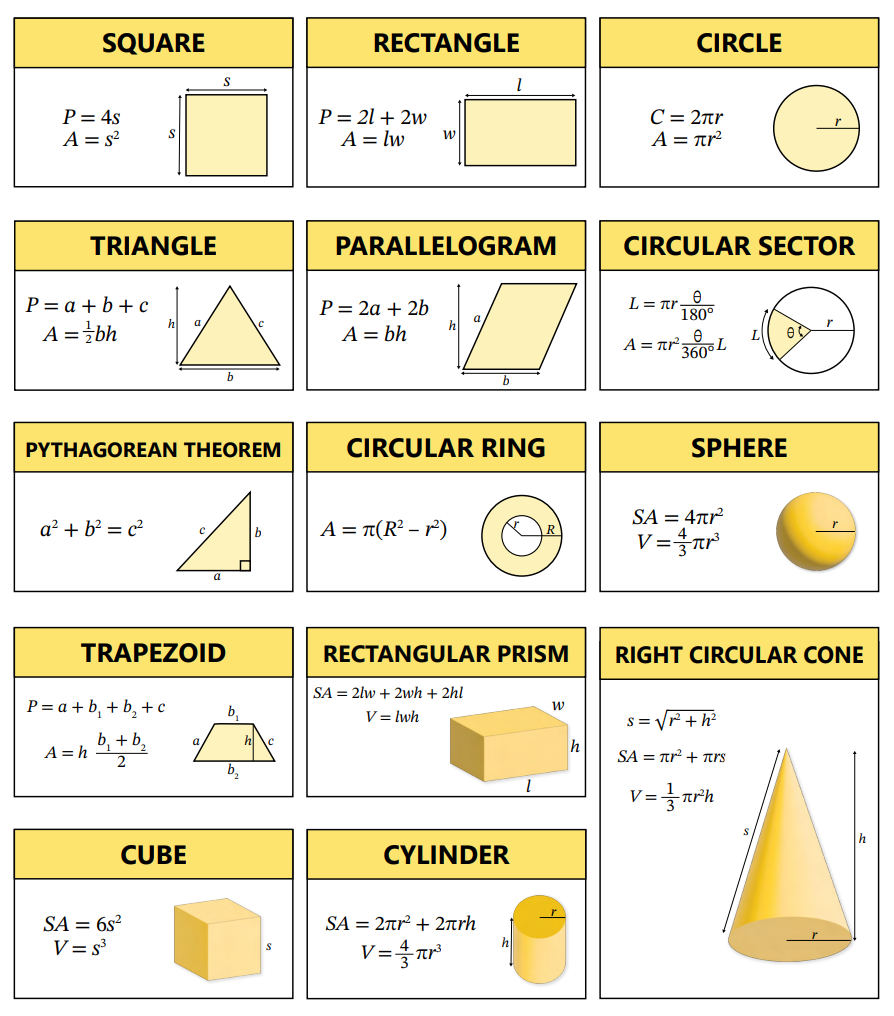
Mometrix’s geometry videos are general reviews of the concepts, ideas, and topics that may be presented on an exam. Each of these videos will give a wide-scope review of what a test taker may need to know as they prepare to take a test.
by Mometrix Test Preparation | Last Updated: December 2, 2024