
Hi, and welcome to this review on similar triangles! Today, we’re going to explore how to identify similar triangles and how we can use that knowledge to solve a very popular kind of geometry problem.
Similar Triangles Definition
Let’s start with a simple definition. Similar triangles are triangles that have the same shape. That means they will have the same three angles. But here’s the twist—similar triangles don’t have to be the same size! So if you take a copy of the triangle and dilate it to twice its size, it will still be similar to the original triangle.
Angle-Angle-Angle Method
Notice that the two triangles have the same shape and proportions. That’s because they have the exact same angles, which is what makes them similar triangles. This is the Angle-Angle-Angle, or AAA, method of determining similarity. It should be noted that anytime you dilate a triangle, you end up with two similar triangles.
Since we know these two triangles are similar triangles, we can express this in math notation like this: \(△ABC\) ~ \(△A’B’C’\)
Okay, but what if we didn’t start by dilating and don’t know all the angles? Is there any other way to tell if two triangles are similar?
Side-Side-Side Method
Let’s look at an example where we only know the lengths of the sides of two triangles:
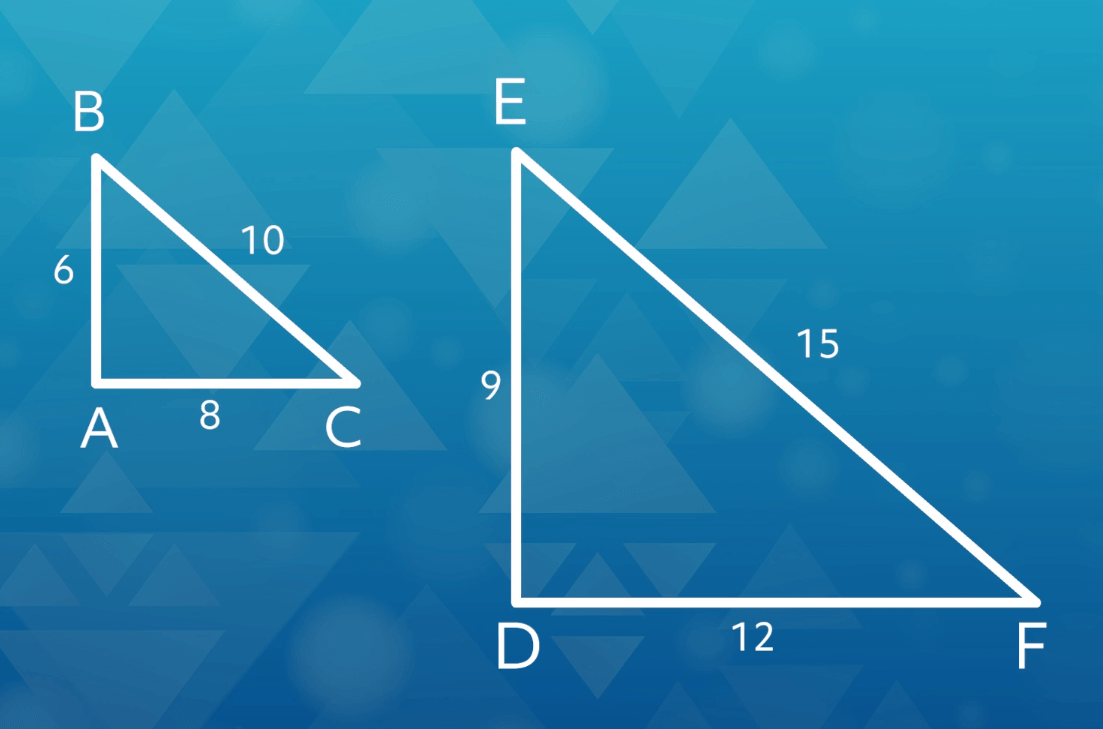
These two triangles appear to be the same shape, but remember that in geometry we can’t always trust our eyes. We need to prove that they are the same shape, and we can do that by checking to see if their sides are in proportion to each other.
We set up our proportions by setting ratios, or fractions, of the corresponding sides and setting them equal to each other, like this: We’ll have the side lengths for \(△ABC\) be the numerators, and the lengths for \(△DEF\) be the denominators. It would work just as well if we switched it around.
It’s very important to label proportions to make sure we put all the numbers in their proper place.
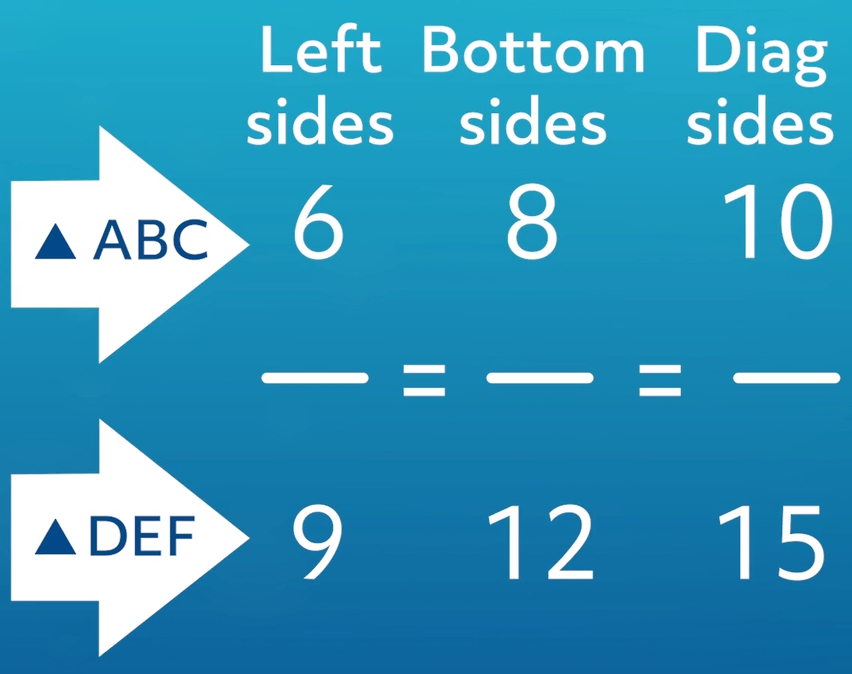
So what does this proportion do for us? Well, we need to test to see if it’s true. In this case, we can do that by reducing each of these fractions to their simplest form.
We can see that 3 goes into the top and bottom of \(\frac{6}{9}\), so we can reduce it to 2 over 3. Four goes into \(\frac{8}{12}\) and 5 goes into \(\frac{10}{15}\). When we reduce those two fractions, we also end up with \(\frac{2}{3}\). In reduced form our proportion looks like this:
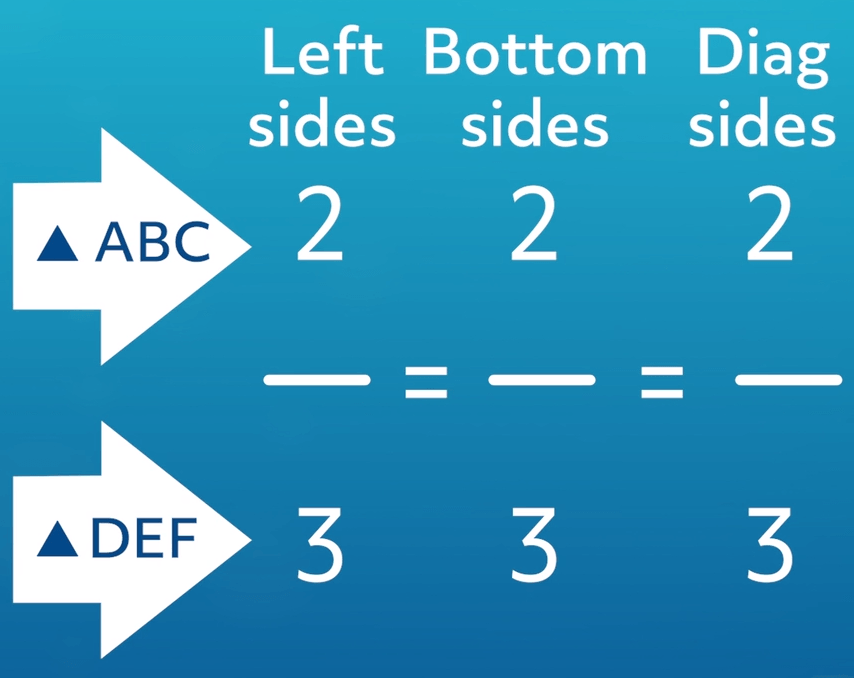
This is proof that all of our sides are in proportion. If all the sides are in proportion, then we know that our triangles are in proportion. This is the Side-Side-Side, or SSS, method of proving similarity. So, now we can say that \(△ABC\) ~ \(△DEF\).
Instead of reducing, we could also check if to see if the ratios are in proportion by converting each ratio to a decimal by dividing the top by the bottom of each. In this case, \(\frac{6}{9}\), \(\frac{8}{12}\), and \(\frac{10}{15}\) would have given us the same decimal value, which is 0.66666666.
So, now we know that if all the angles are the same, or if all the sides are in proportion, our two triangles are similar.
Side-Angle-Side Method
There is one more method of proving similarity called Side-Angle-Side, or SAS. This is where we know the two triangles have one angle that is the same measure and that the two sides coming off that angle are in proportion.
Let’s take a look at our last two triangles, but instead of knowing all three sides, we only know two sets of corresponding sides along with the angle between them, like this:
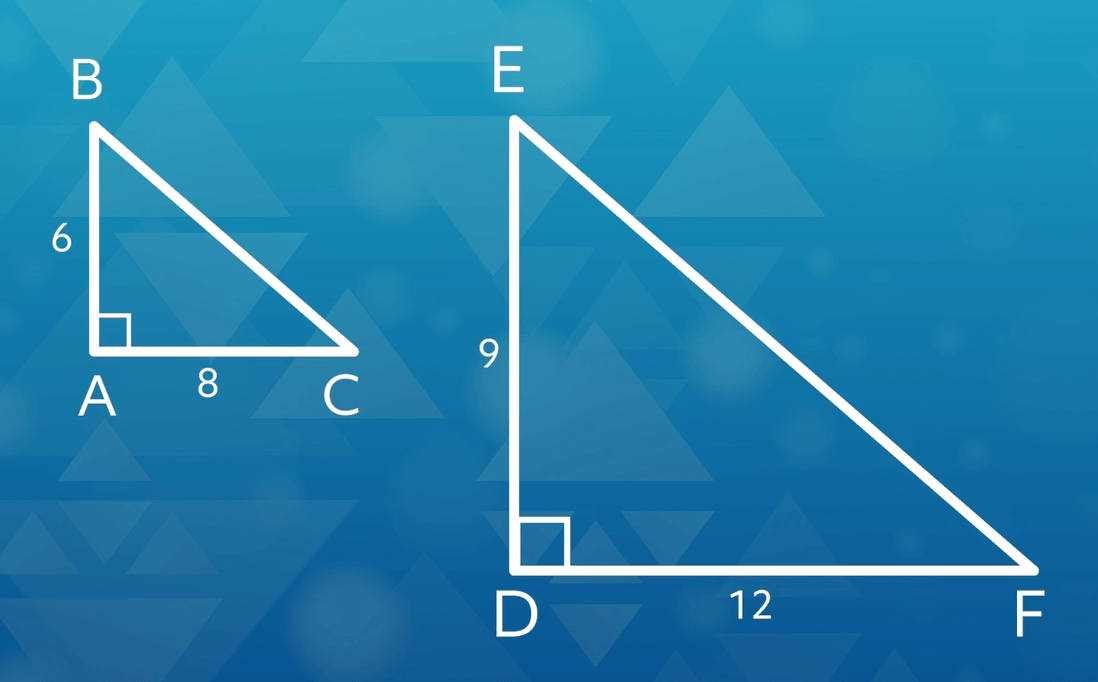
We can see that the angle between the two measured sides is labeled with a square, which we know means that it’s a right angle and therefore 90 degrees. Since that angle is the same in both triangles we just need to check to see if the two adjacent sides are in proportion, like this:
Reducing the fractions again results in them being 2 over 3, so the sides are in proportion. Since the angle between those sides is the same, or congruent, this triangle is similar.
Height of the Tree Problem
Okay, so what can we do with this ability to recognize similar triangles? You’ve may have seen it before, but here is the classic height of the tree problem:

Here’s what we know. The tree and the flagstick are both standing straight up perpendicular to the ground. They are each casting a shadow from the same light source, the sun. The rays coming from the sun are straight lines shining on the objects at an angle. The ground is flat and can be considered a flat plane, which means any two points on it can be connected with a straight line. That means I can draw two triangles over this drawing, like this:

Now, let’s keep our triangles but lose the pretty scenery.
Next, let’s label all the points so we can reference them. It doesn’t matter what letter we use for each point.
We also know that angle B and angle D are right angles since the flagstick and the tree are pointing straight up perpendicular to the ground, so we’ll label that too:
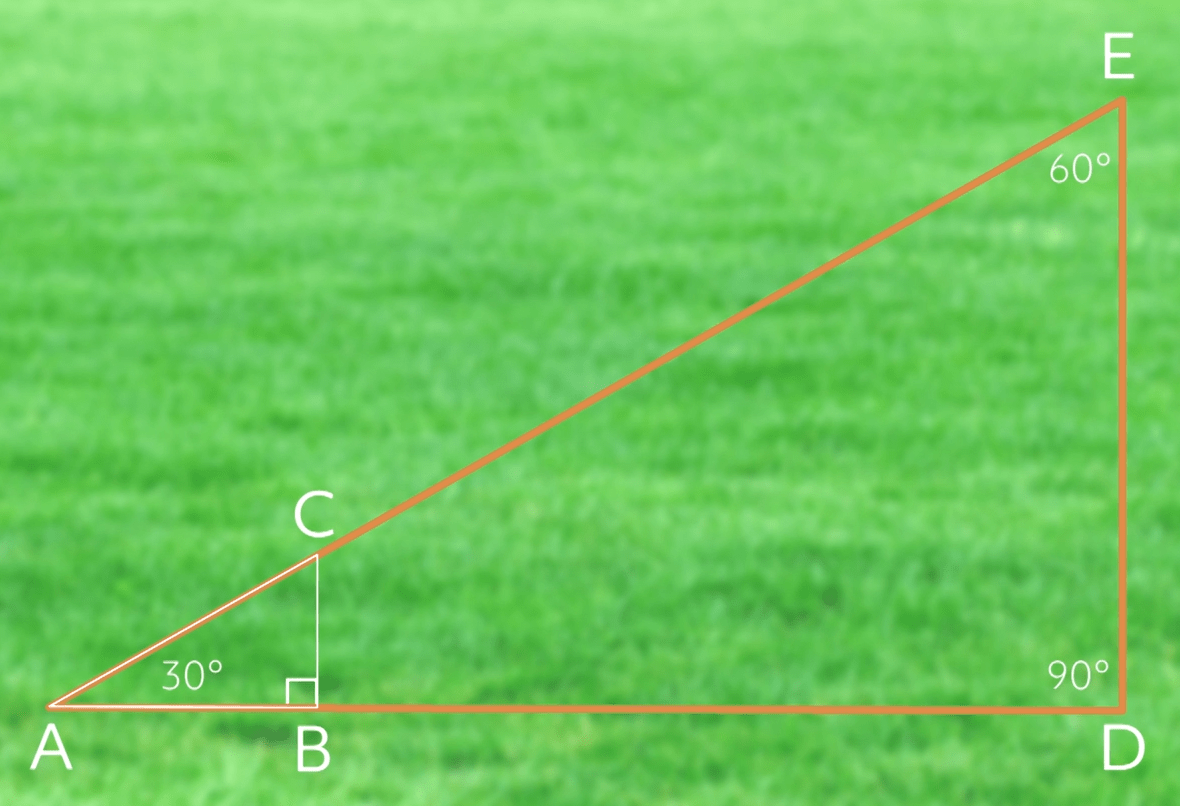
Since we know that angle A is the same for both triangles and that angles B and D are both right angles and therefore congruent, that means that angles C and E are also congruent. Why? Because the interior angles of a triangle must add up to 180°. So if A is 30° and B and D are 90°, then C and E will end up being 60°.
Now we know they are similar triangles using the AAA method of proving similarity.
Now we can get to the fun part and use these triangles to find the height of the tree. First, we’ll need to take some measurements. We need to measure the flagstick, the length of the shadow of the flagstick, and the length of the shadow of the tree. Fortunately, these are all easy to do. A standard golf flagstick is 7 feet tall. The shadows are on the ground, obviously, so we can measure them with a long tape measure. Then we can add them to our triangles.
Since the sides of similar triangles are always in proportion, we can set up a proportion with all rows and columns labeled:

We don’t know either of the diagonal sides but we don’t need them for this type of problem. We know the ground sides of both triangles and we know the height of \(△ABC\). We can place a variable for the height of the tree, which is \(\overline{DE}\) in our triangle. Now we just use cross products to solve:
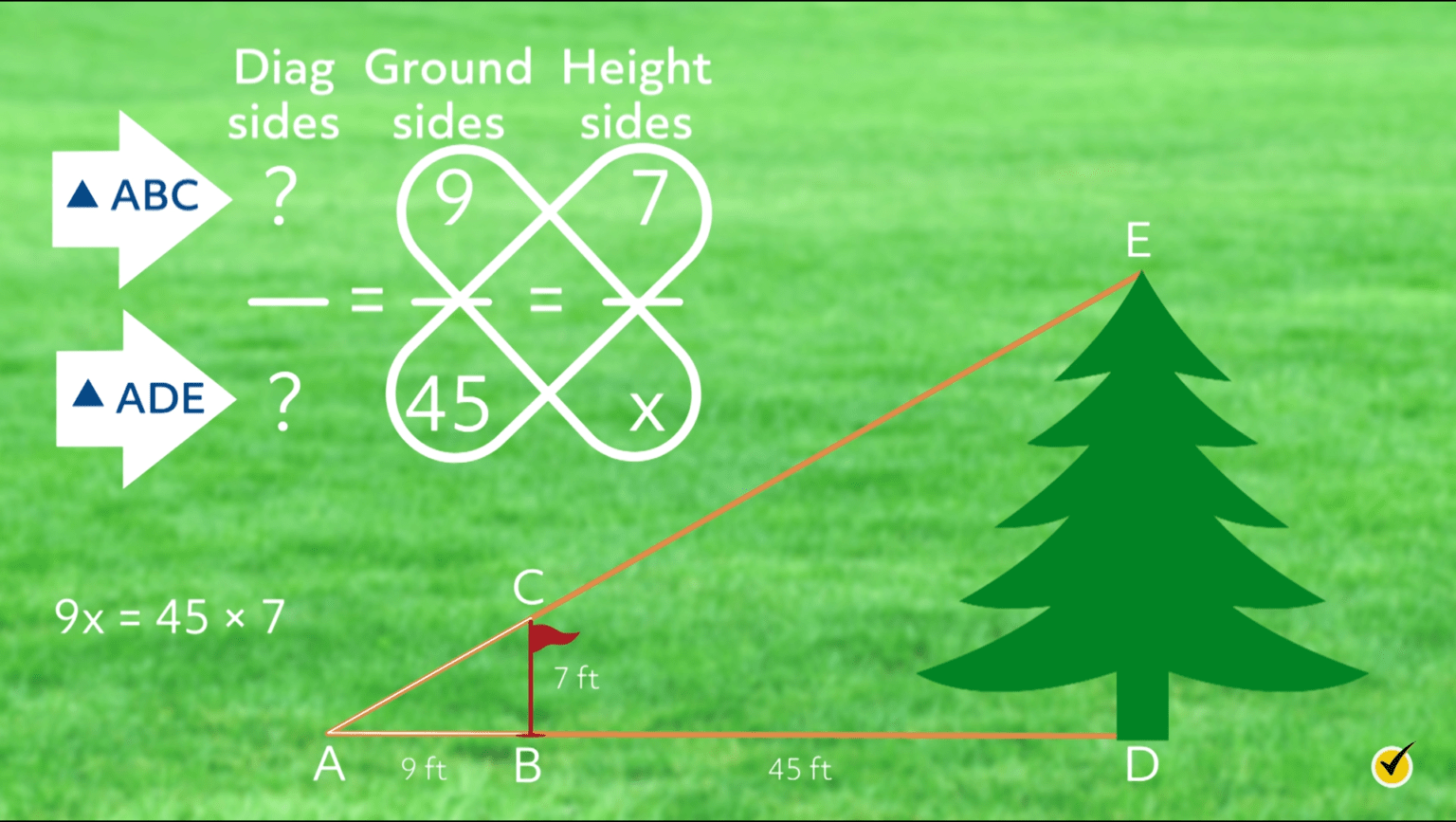
Taking cross products results in the equation \(9x=45\cdot 7\), or \(9x=315\) after we multiply 45 and 7. Dividing both sides by 9 gives us \(x=35\). So our tree is 35 feet tall!
Review
Ok, now that we’ve covered everything, let’s do a quick recap:
Similar triangles are triangles that have the same shape. There are three ways to prove that two triangles are similar. The AAA method of similarity is when the proportions of all three angles of the triangles are the same. The SSS method is when all three sides of the triangles are the same length. And finally, the SAS method is when the two triangles have one angle that is the same measure and the two sides coming off that angle are in proportion.
I hope this review was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What are similar triangles?
A
Similar triangles are triangles whose corresponding angles are equal and whose corresponding sides are proportional but not necessarily equal.
Ex. 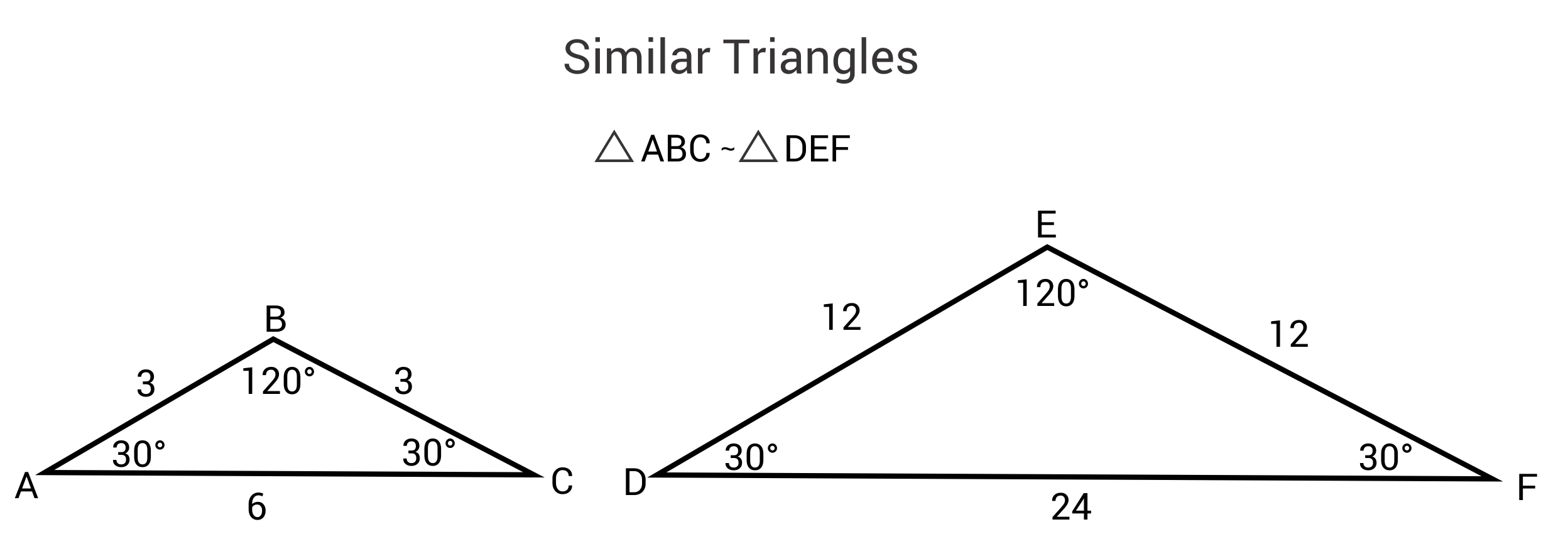
Q
Are all right triangles similar?
A
No, not all right triangles are similar. For triangles to be similar, they must have the same angle measures. All right triangles have one right angle, but the other two angles can be any combination of measures that add to 90°.
Ex. ⊿ABC is not similar to ⊿DEF.
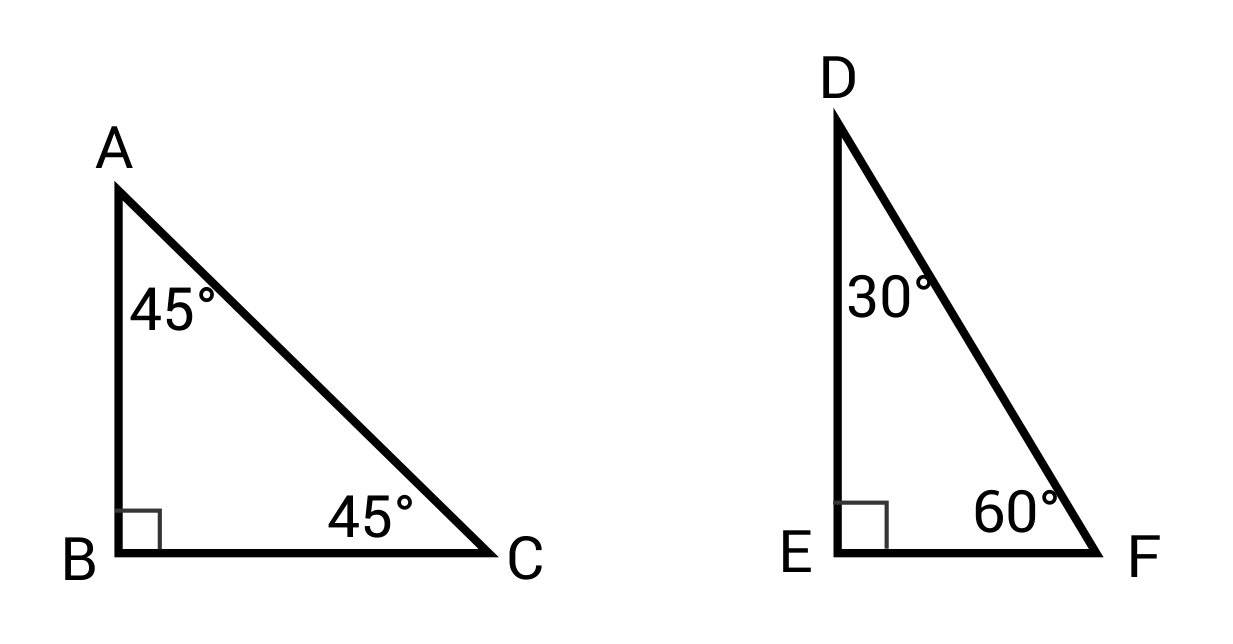
Q
Are all equilateral triangles similar?
A
Yes, all equilateral triangles are similar because they all have the same angle measures.
Q
Are all isoceles triangles similar?
A
No, not all isosceles triangles are similar. In order for triangles to be similar, they must have the same angle measures. Not all isosceles triangles have the same angle measures.
Ex. ⊿ABC is not similar to ⊿DEF
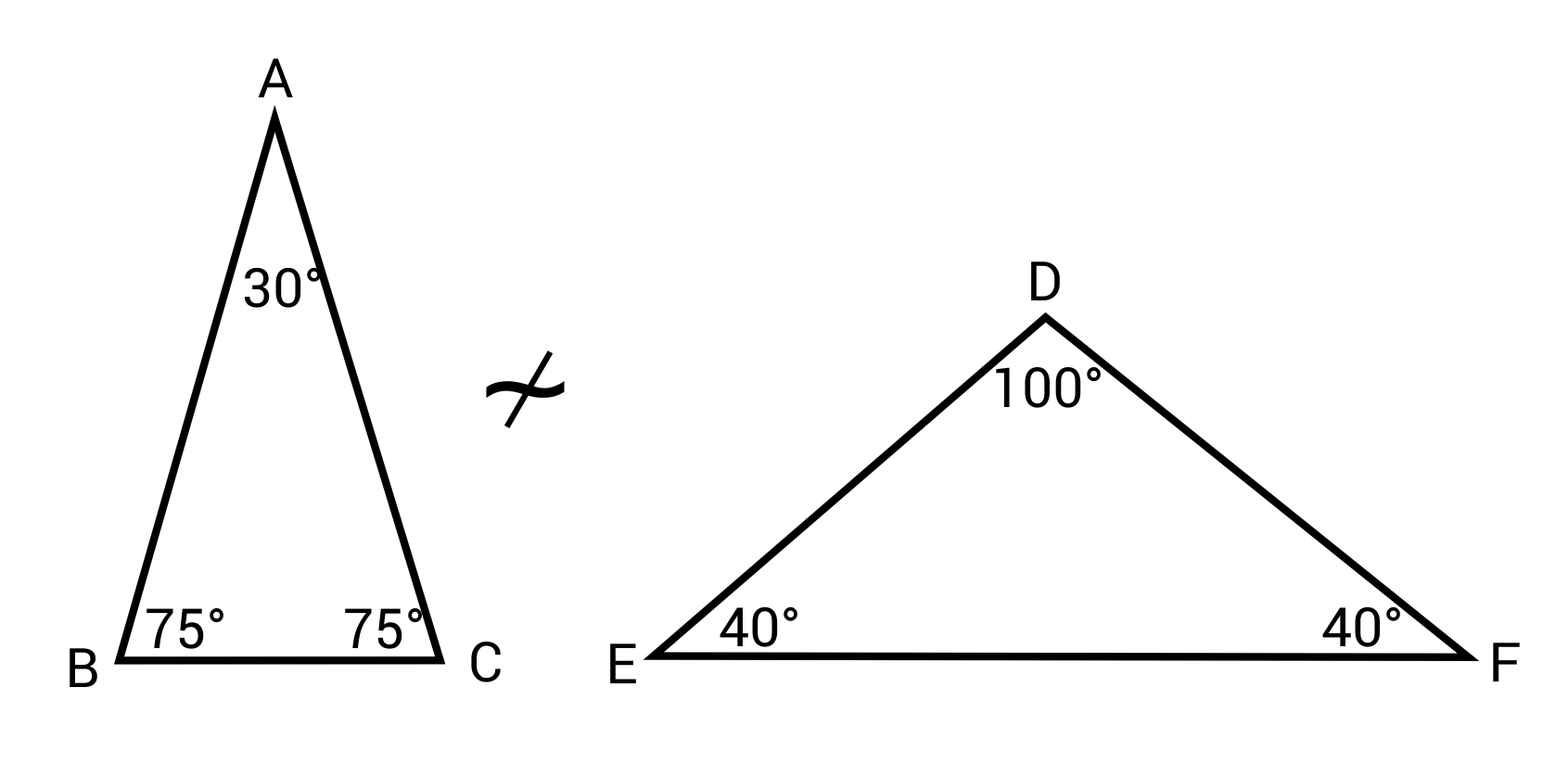
Similar Triangle Practice Questions
Which of the following statements is not true about similar triangles?
The correct answer is they are the same size. Similar triangles are triangles that have the same shape, same angle measures, and are proportional to one another. Similar triangles are not the same size. If triangles are the same size, then they are congruent.
△ABC is similar to △DEF. Find x.
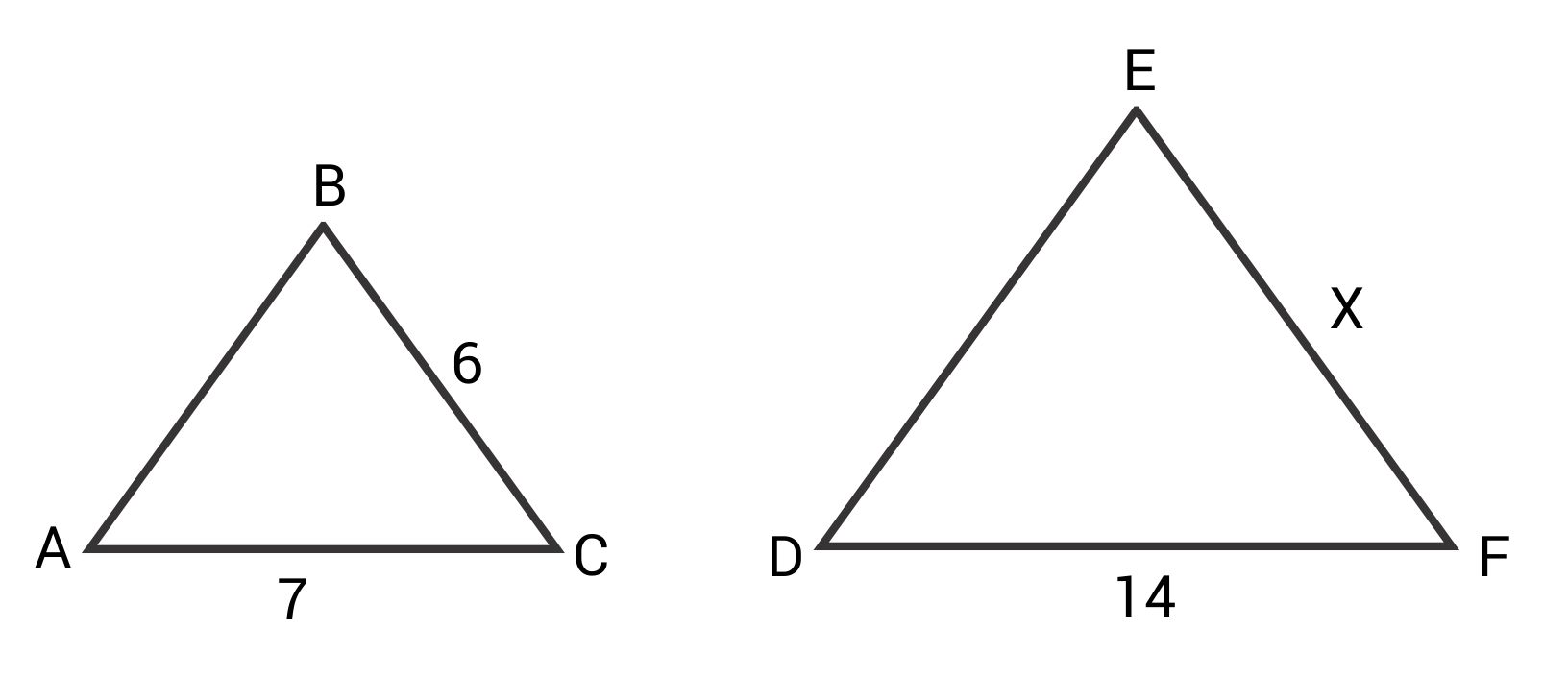
The correct answer is 12. Because the triangles are similar, their sides are proportional. \(\overline{BC}\) is proportional to \(\overline{EF}\) and \(\overline{AC}\) is proportional to \(\overline{DF}\). Set up a proportion.
\(\frac{6}{x}=\frac{7}{14}\)
Cross multiply and solve for x.
\(6\times14=7x\)
\(84=7x\)
\(12=x\)
△ABC is similar to △DEF. Find x.
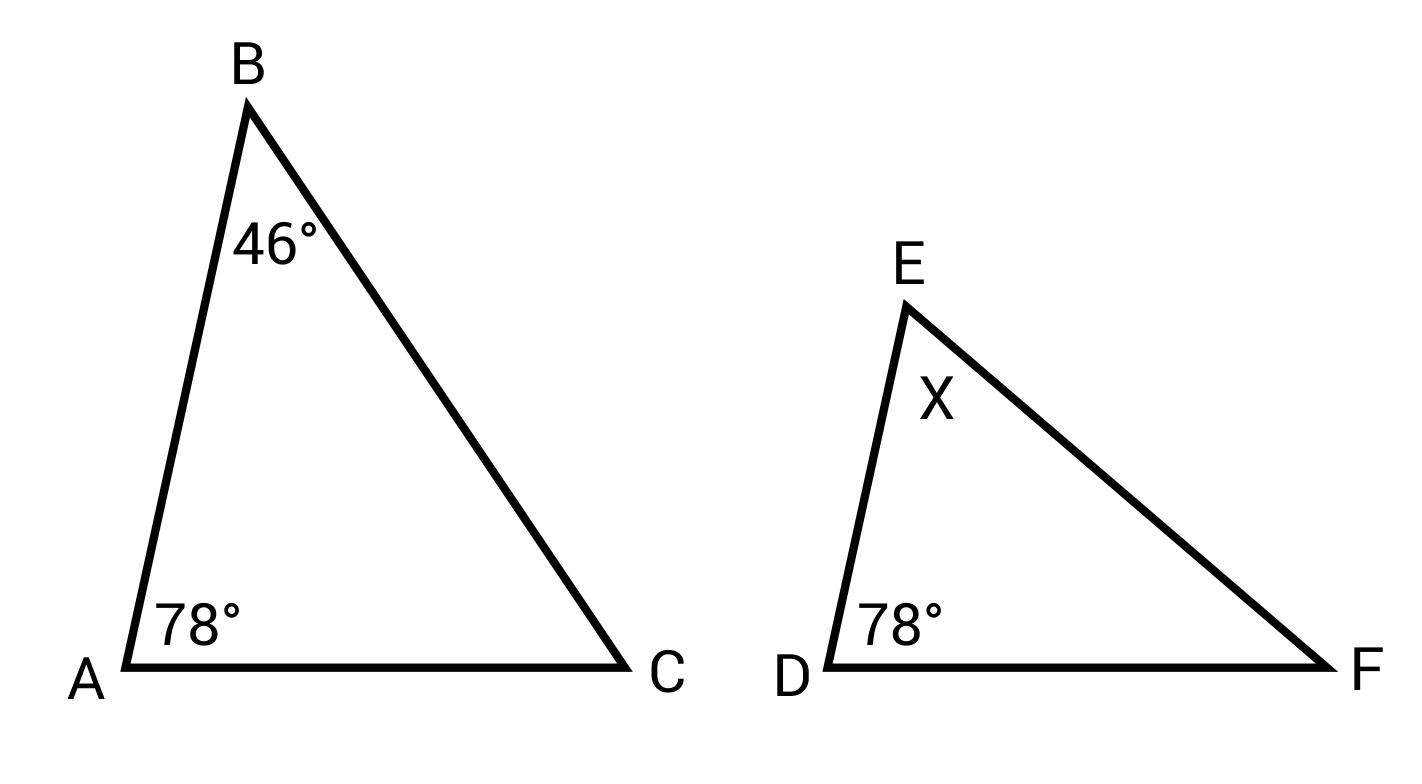
The correct answer is 46°. Similar triangles have congruent angle measures. Since ∠B = 46°, ∠E also must be 46°.
Are these two triangles similar?
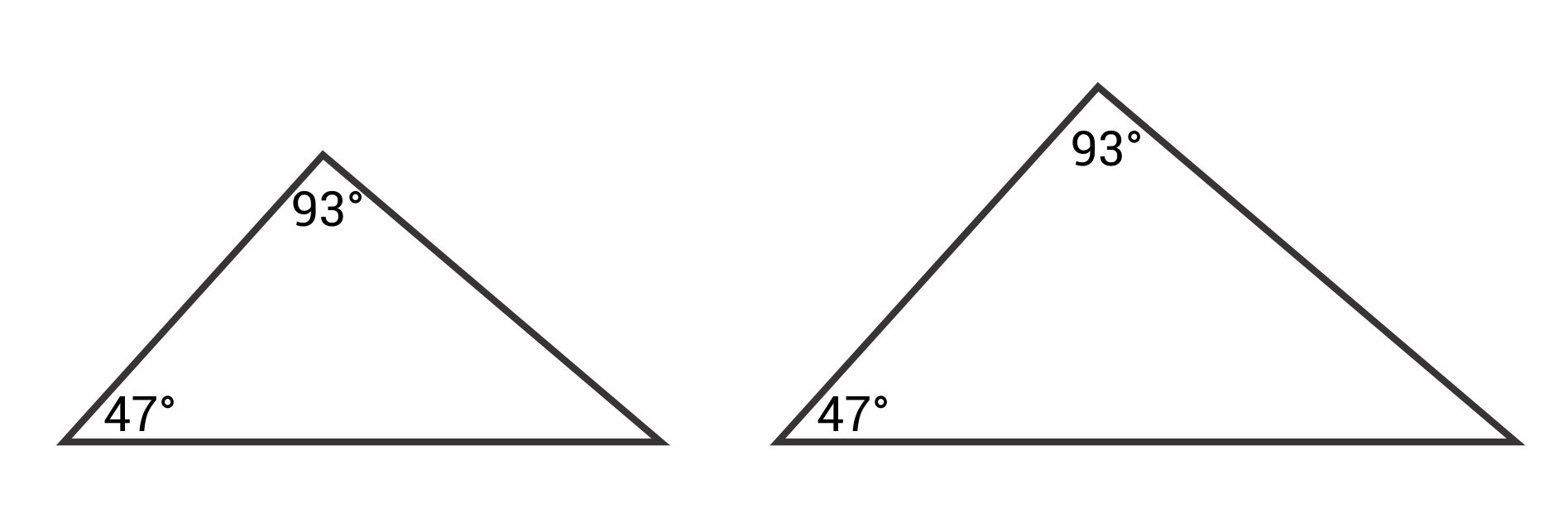
The correct answer is yes. Similar triangles must have congruent angle measures. Since two of the angles are known in each triangle and are the same, they can be determined to be similar triangles because the third angles must also be the same. All triangles have interior angles that add to 180°, so the third angle in both these triangles must be \(180°-93°-47°=30°\).
△ABC is similar to △DEF. Find x.
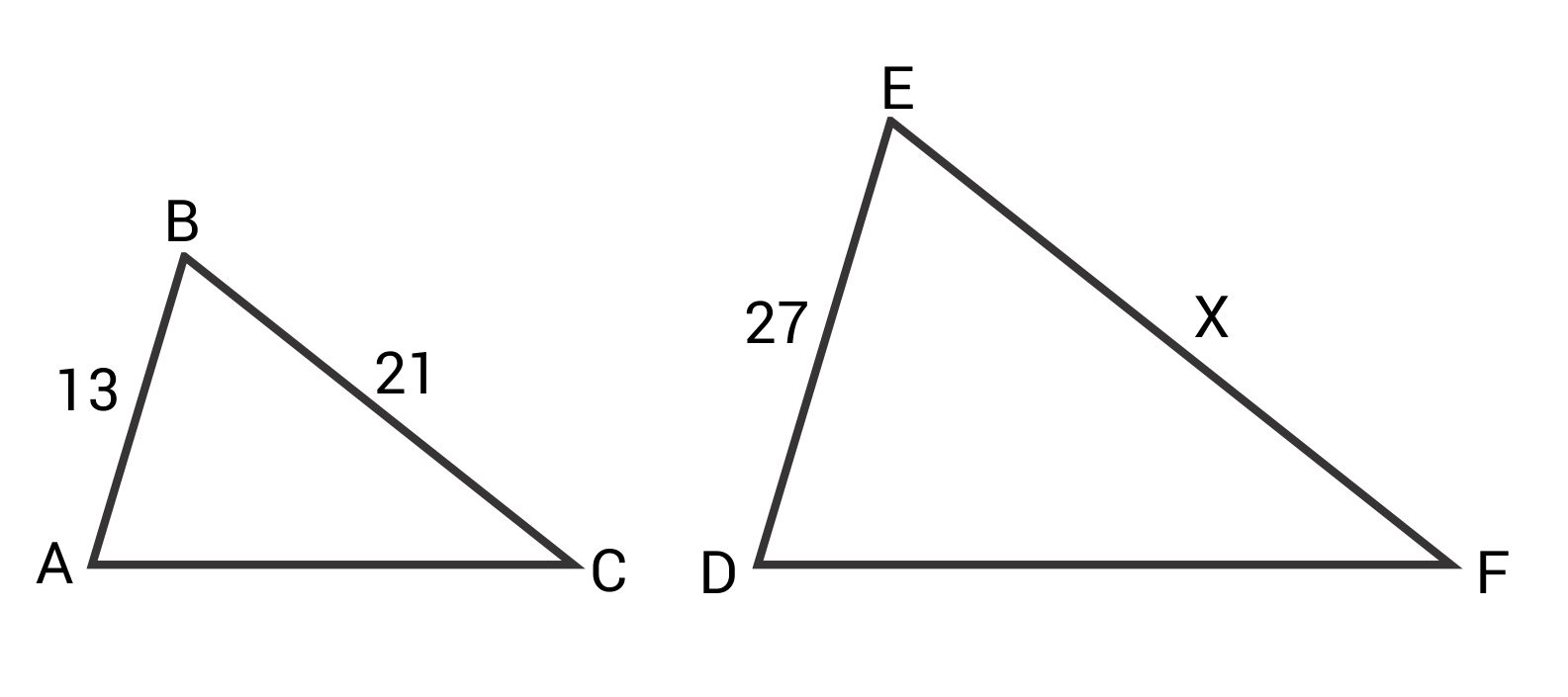
The correct answer is 43.62. Because the triangles are similar, their sides are proportional. \(\overline{AB}\) is proportional to \(\overline{DE}\) and \(\overline{BC}\) is proportional to \(\overline{EF}\). Set up a proportion.
\(\frac{13}{27}=\frac{21}{x}\)
Cross multiply and solve for x.
\(13x=21\times27\)
\(13x=567\)
\(x≈43.62\)
