
Hi, and welcome to this video about angles.
What is a Ray?
Let’s start by defining a ray. A ray is a line with a single endpoint that extends infinitely in one direction.

If we take this ray and add another ray to it that has the same endpoint, we’ve created an angle.

What is a Vertex?
We’ve also created a vertex, which is the point where the two rays meet.
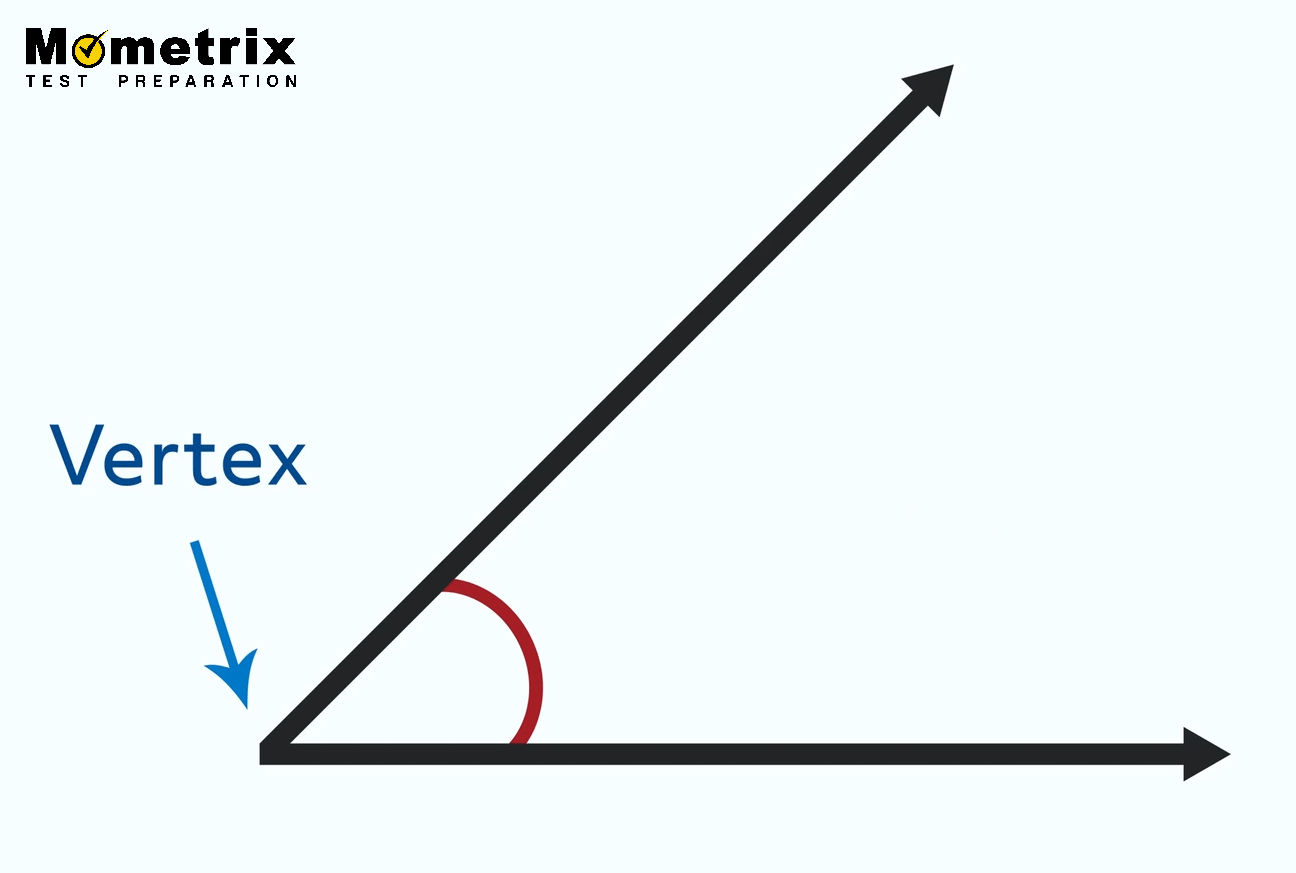
You can think of it as a corner. We usually see vertices whenever lines meet or in polygons like triangles and quadrilaterals.
Labeling Angles
Sometimes we have many angles, so in order to tell them apart, we have a system for naming them. Here’s our simple angle again but with a few points added on the rays:
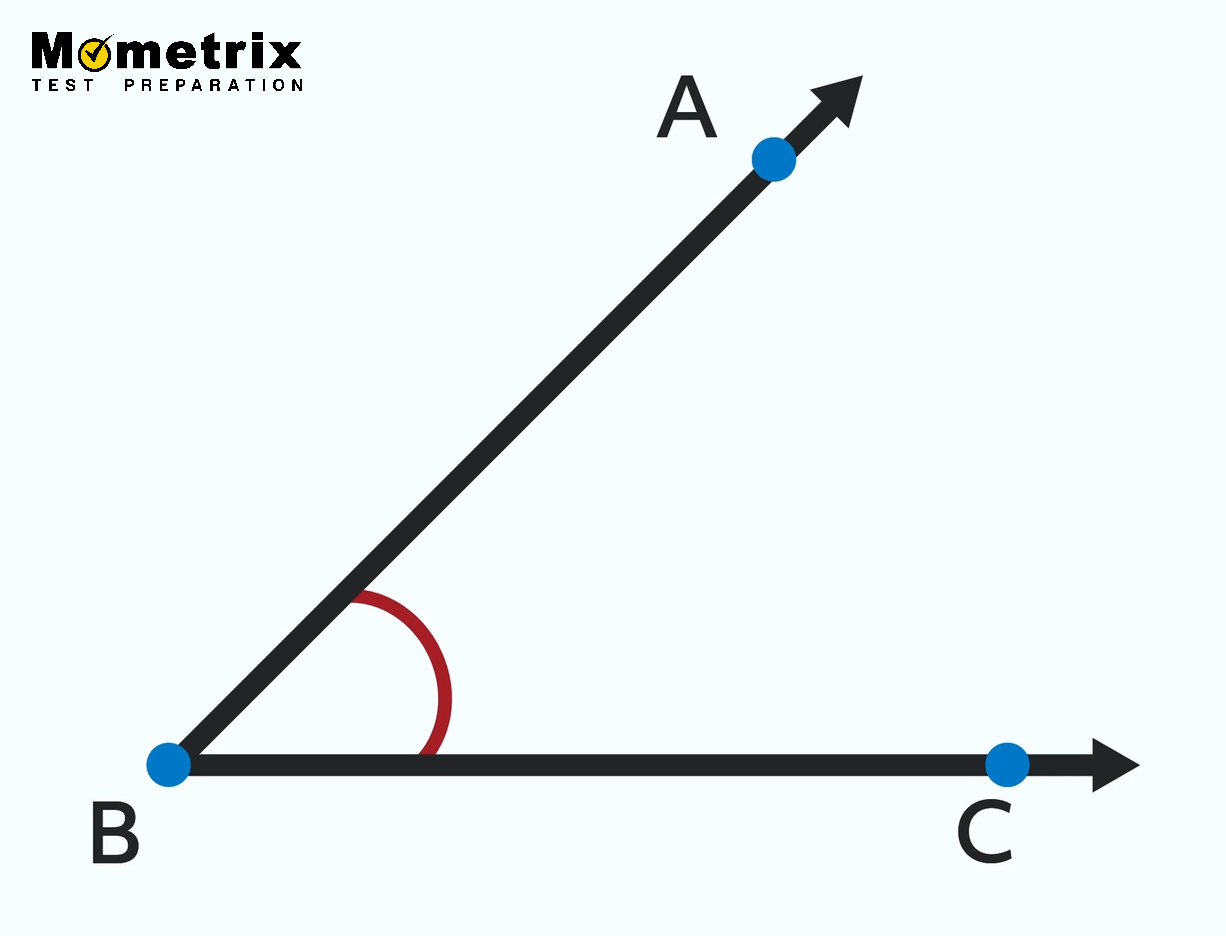
Now we can refer to our angle as angle ABC (∠ABC). When naming angles with three letters, the vertex point must be in the middle. Here, B is the vertex so the B goes between the A and the C. We can actually call this ∠CBA and it is just as correct.
If the point that is the vertex is only a part of one angle then we can use a shorter name. In this case, we could also call this angle B. Be careful though, because sometimes a single point can be the vertex of multiple angles, like this:
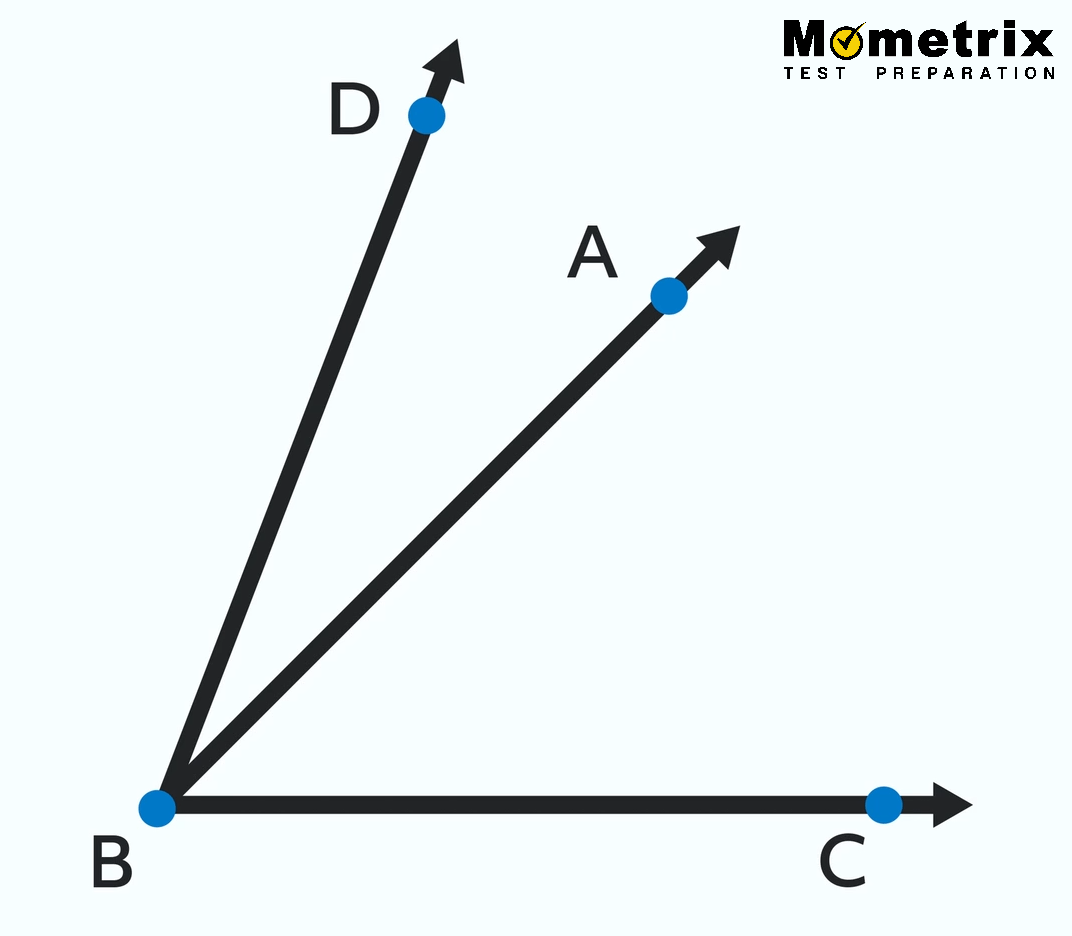
In this case, we’d have to call the angles by their long names, because point B is the vertex of ∠ABC, ∠DBC, and ∠DBA! If we asked someone to just look at ∠B they wouldn’t know which of these we meant. So it’s important to be precise when dealing with more than one angle.
Sometimes angles will be labeled with numbers inside the arc, like this:
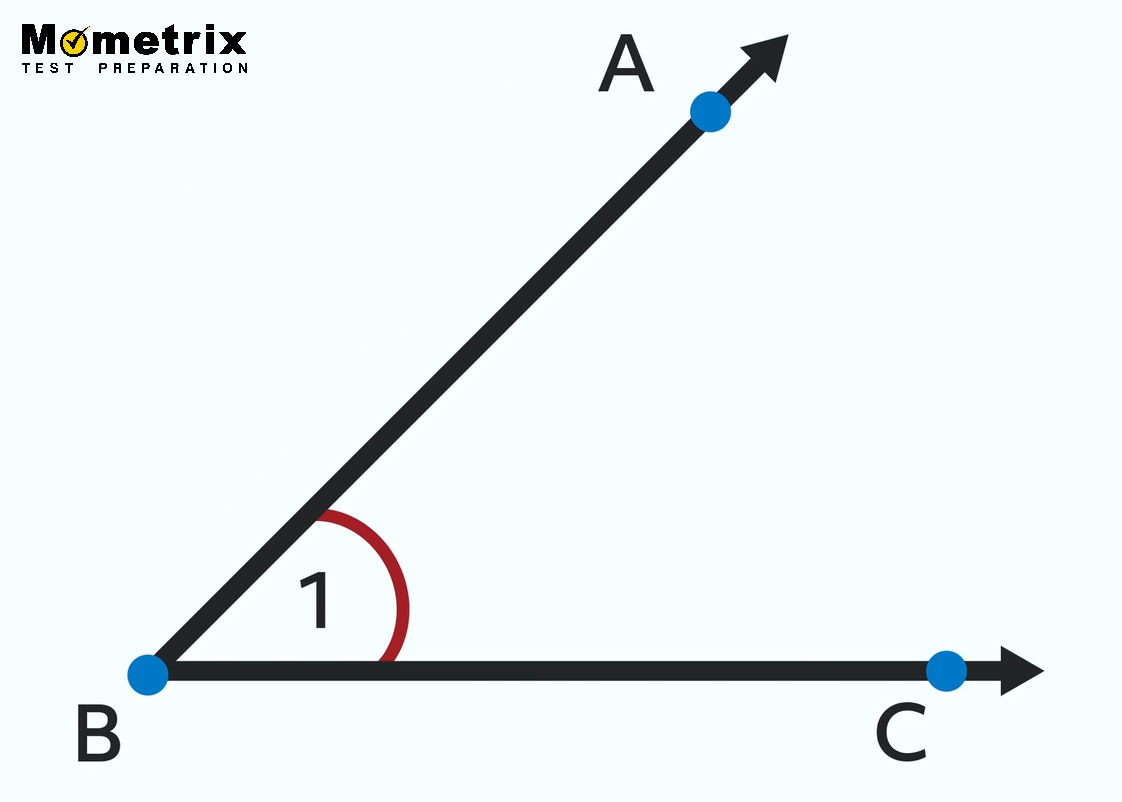
Now we have an additional name for this angle. We can now call it ∠1 or we can call it ∠ABC or we can call it ∠B. Since most of us have three names, it’s only fair that angles have a bunch too. But most of the time we like to use letters to name our angles, since the numbers could be confused with the measure of an angle. Sometimes you’ll see lowercase letters instead of numbers or Greek symbols like \(\theta\) or \(\alpha\).
Measuring Angles
Speaking of measuring, remember the protractor? We use it to measure angles. If we were to place one on our trusty angle we would find that it measures 45 degrees:
If we wrote this out, we would write it like this:
The measure of an angle is important in classifying angles, as we’re about to see.
Let’s look at a variation of our two-ray angle, but this time let’s make it so that they are perpendicular to each other, which means the angle between them is 90 degrees:
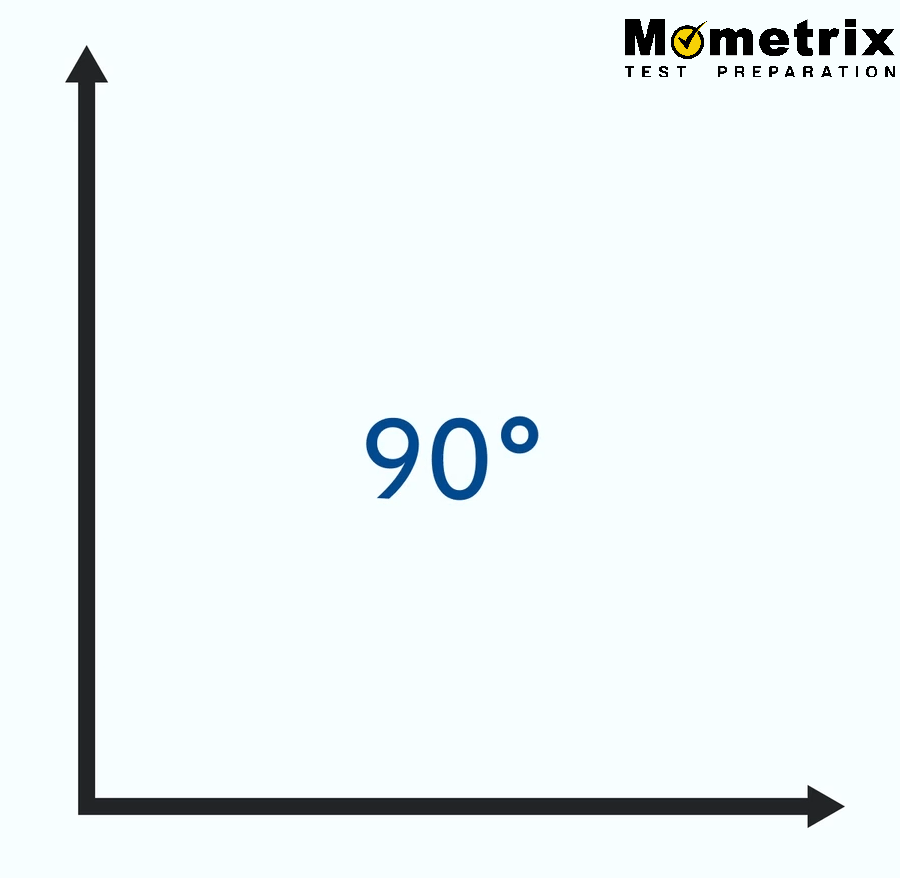
Here, we’ve created a right angle. Notice that it has a different angle symbol than our first angle. Instead of an arc, it has a square. Whenever we see an angle with that square we know it is exactly 90 degrees. We most often see right angles in squares, rectangles, and right triangles, but they can appear in other places too.
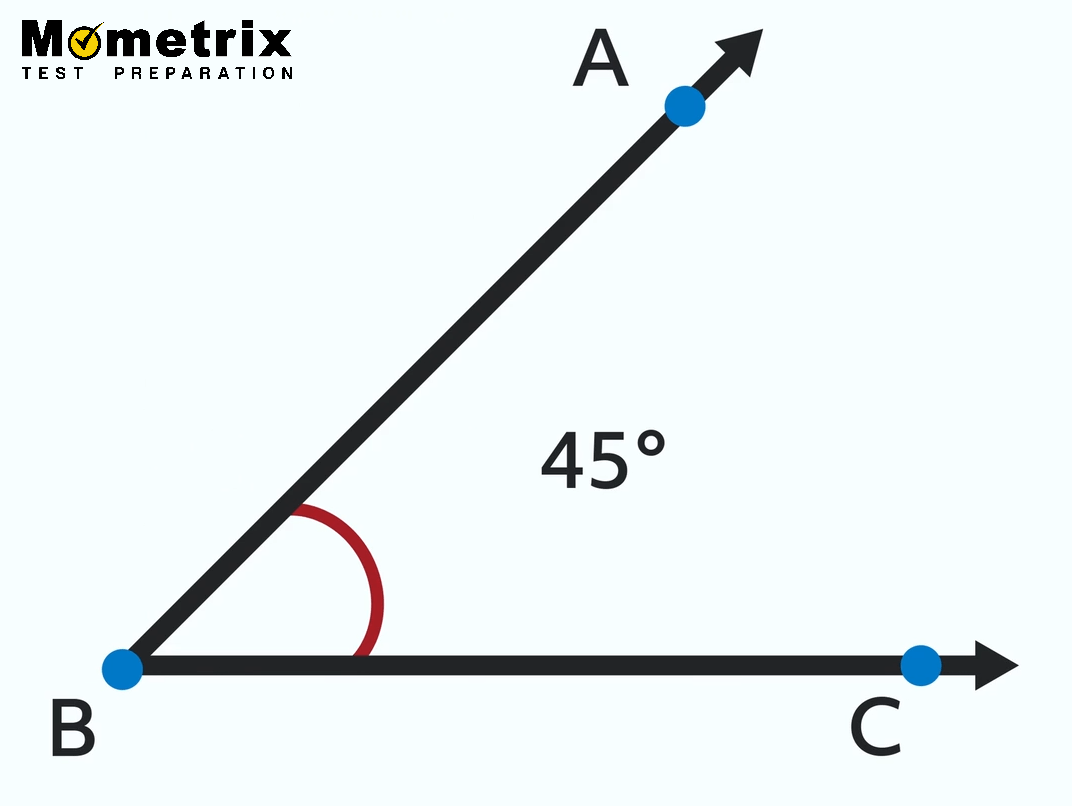
When an angle has a measure that is smaller than 90 degrees, it’s called an acute triangle. Our original angle would be part of an acute triangle, since it measures 45 degrees, which is less than 90:
If we make an angle so that it has a measure that is greater than 90 degrees, we create an obtuse angle, which looks like this:
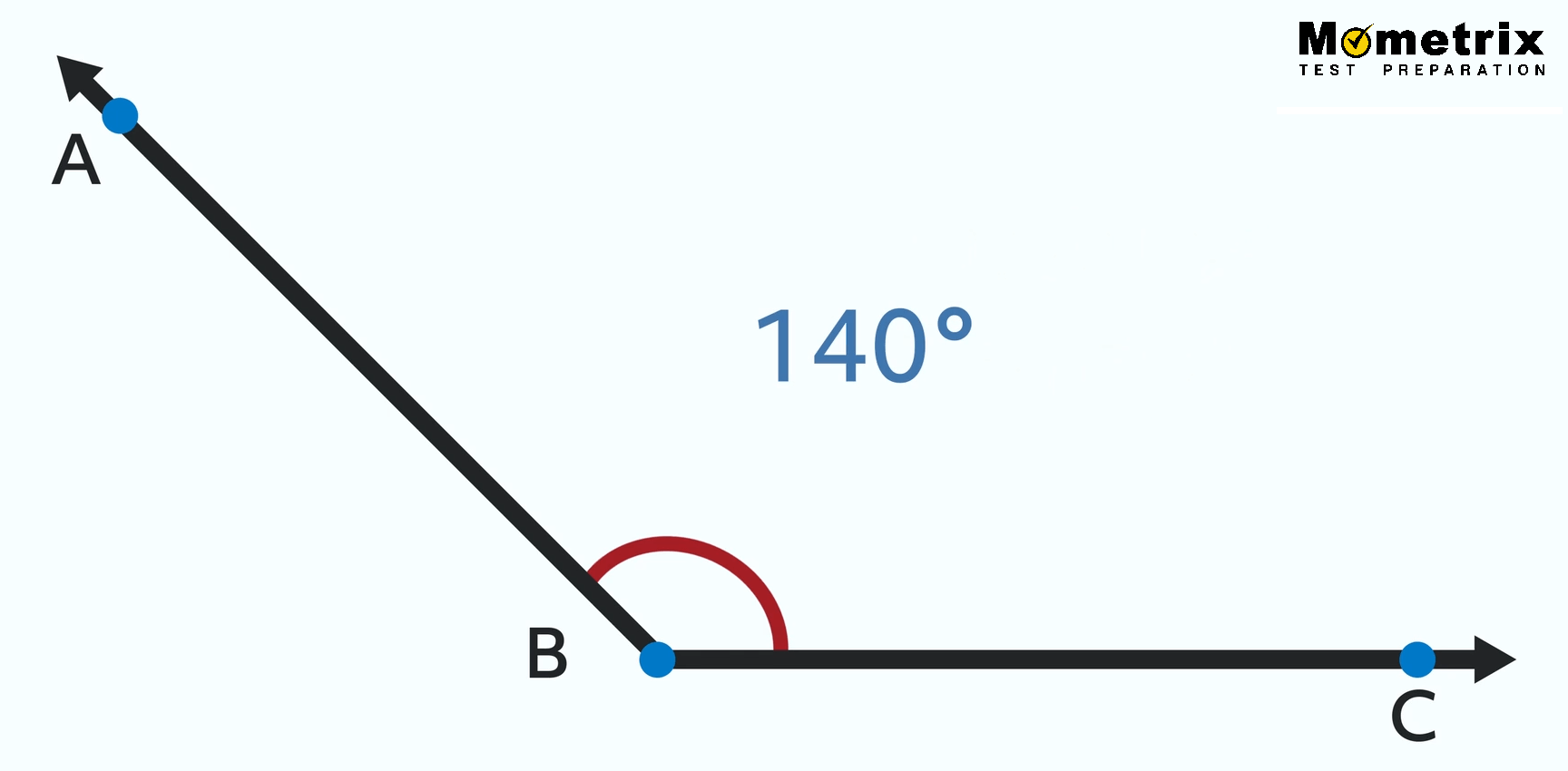
In this case, angle ABC has a measure of 140 degrees, which is greater than 90. Obtuse angles also have to be less than 180 degrees.
Those are the three main types of angles as determined by measure, but there are two more oddballs we need to know about.
The first is a straight angle. It looks like a straight line, and it has a measure of 180 degrees.
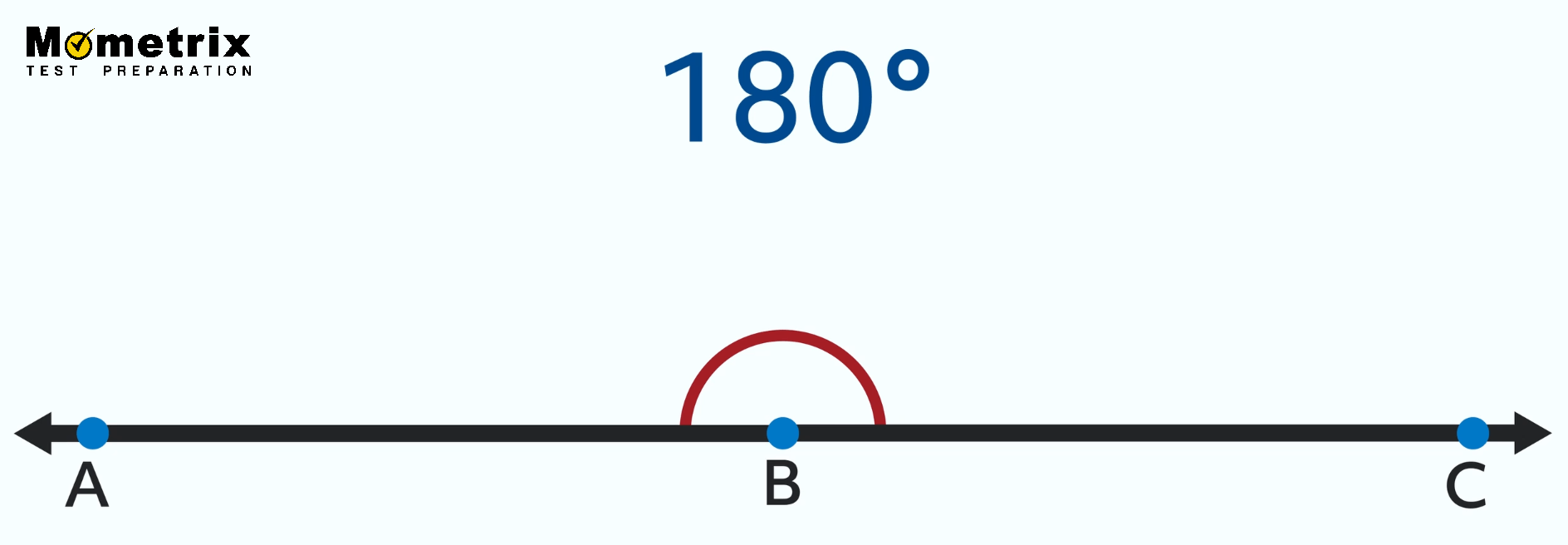
When it’s drawn like this, we can see that ∠ABC does exist and has a measure of 180 degrees. This is a useful thing to know because we’ll need it to understand linear pairs later on.
But before we get to that, let’s look at the other oddball. This one doesn’t look like an angle at all:

But in fact, it’s called a full angle. Imagine we rotated point A counterclockwise, with point B staying where it is, until it lined up with point C again. How many degrees is that? It’s all the way around the circle, which we know is 360°.
Remember our straight angle? What if we drew that but added another ray sticking out of it, like this:
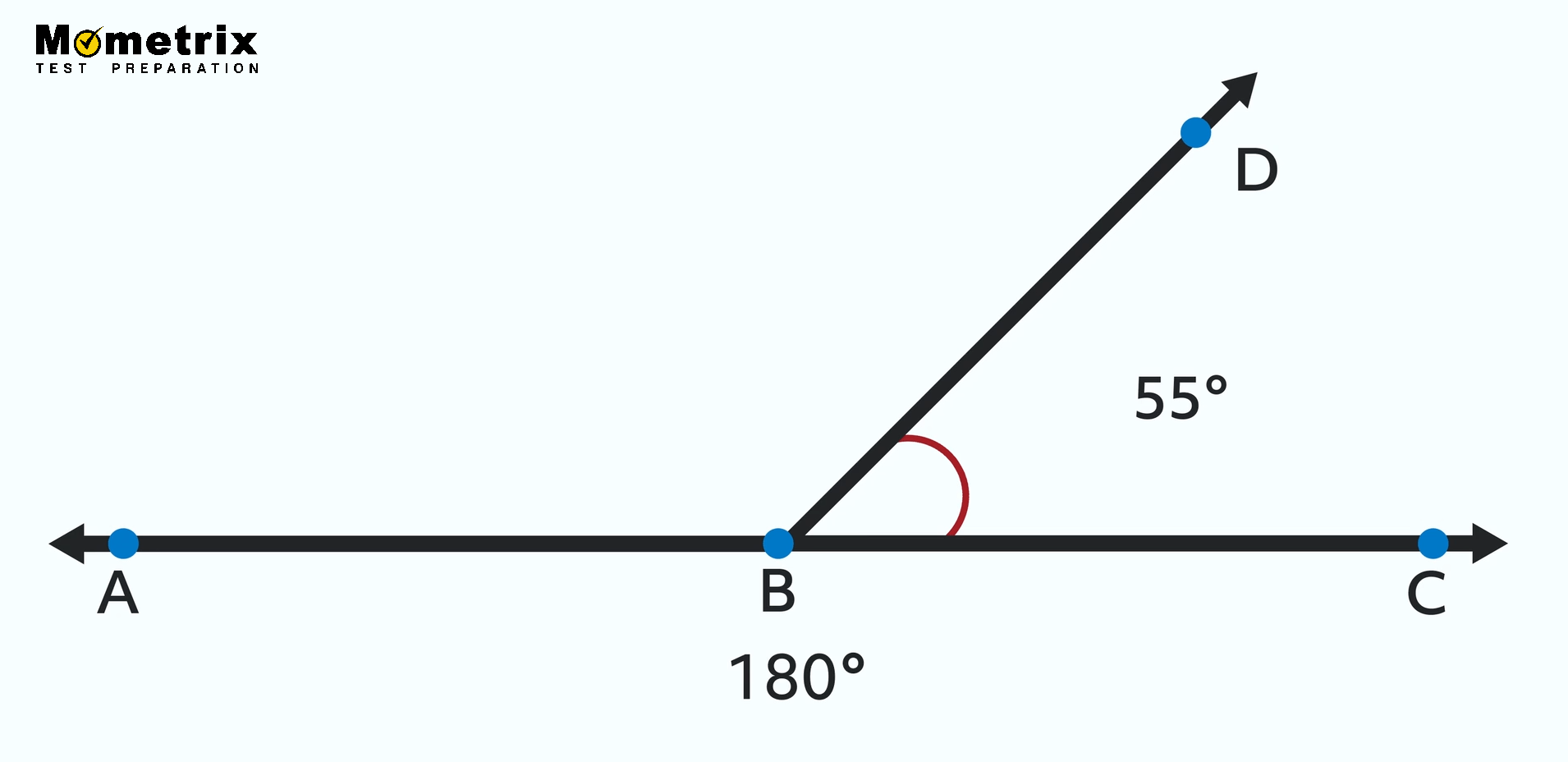
If we know that angle DBC is 55 degrees, and we know that angle ABC is a straight angle and therefore 180 degrees, we can actually find angle ABD! How? By taking the whole straight angle (∠ABC) that measures 180 degrees and subtracting the smaller angle (∠DBC) that measures 55 degrees. \(180° – 55° = 125°\). This is called a linear pair.
Two angles (∠ABD & ∠DBC) combine to form ∠ABC, which is a line. And because the two smaller angles add up to 180 degrees, we can also say that they are supplementary angles.
Something very similar happens with right angles. Here’s our right angle from before, but with another ray in the middle:
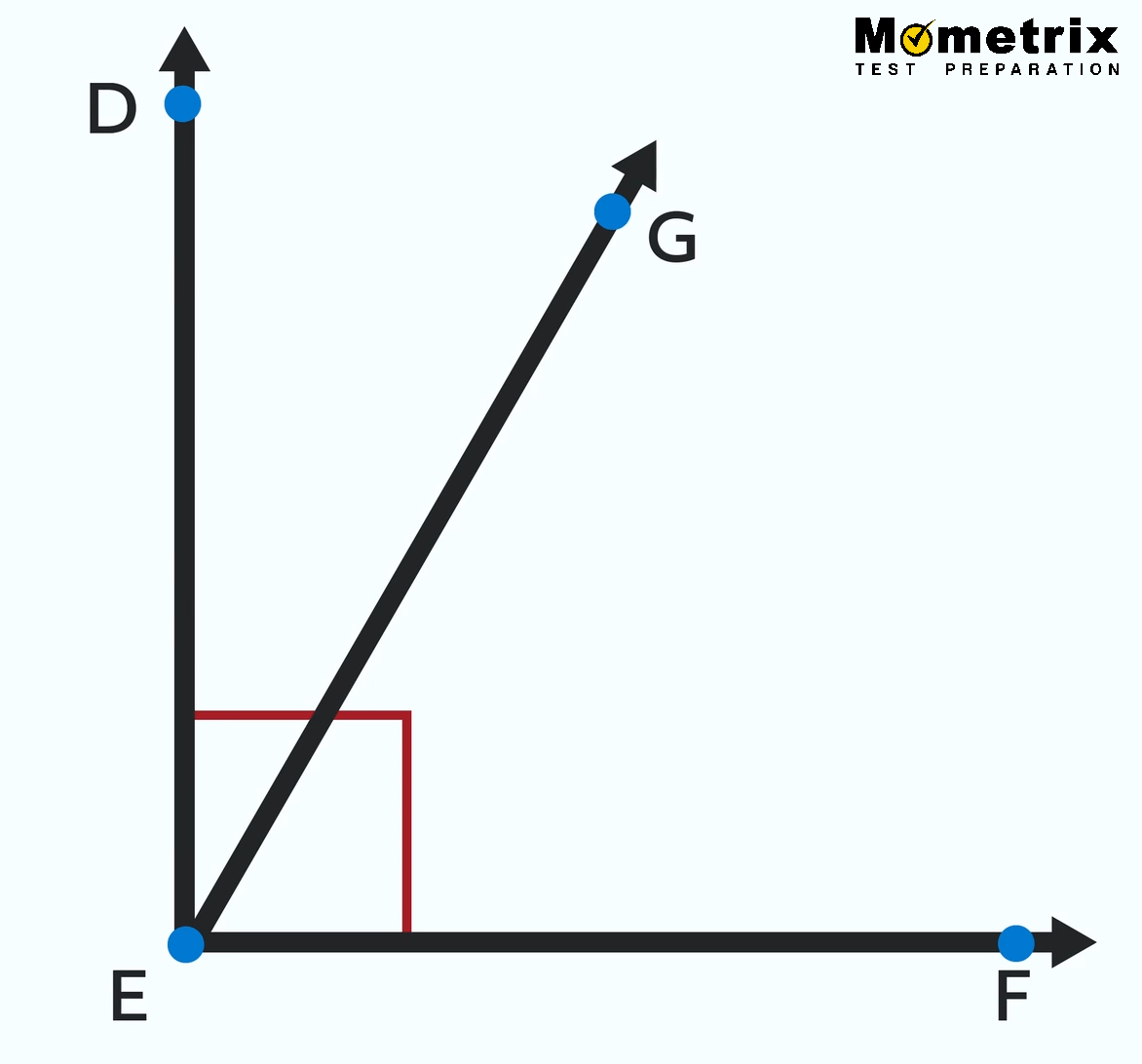
Angle DEF is a right angle. We can see that ∠DEG and ∠GEF together completely fill ∠DEF, which means they add up to 90 degrees. So if we know one of the two angles we can find the other one by subtracting its measure from 90 degrees. For instance, if ∠DEG is 30° then we know that ∠GEF is 60° because 90° – 30° = 60°. Angles that add up to 90° are called complementary angles.
Let’s go back to our obtuse angle one more time. There’s one more type of angle that’s been hiding in plain sight that we need to be aware of.
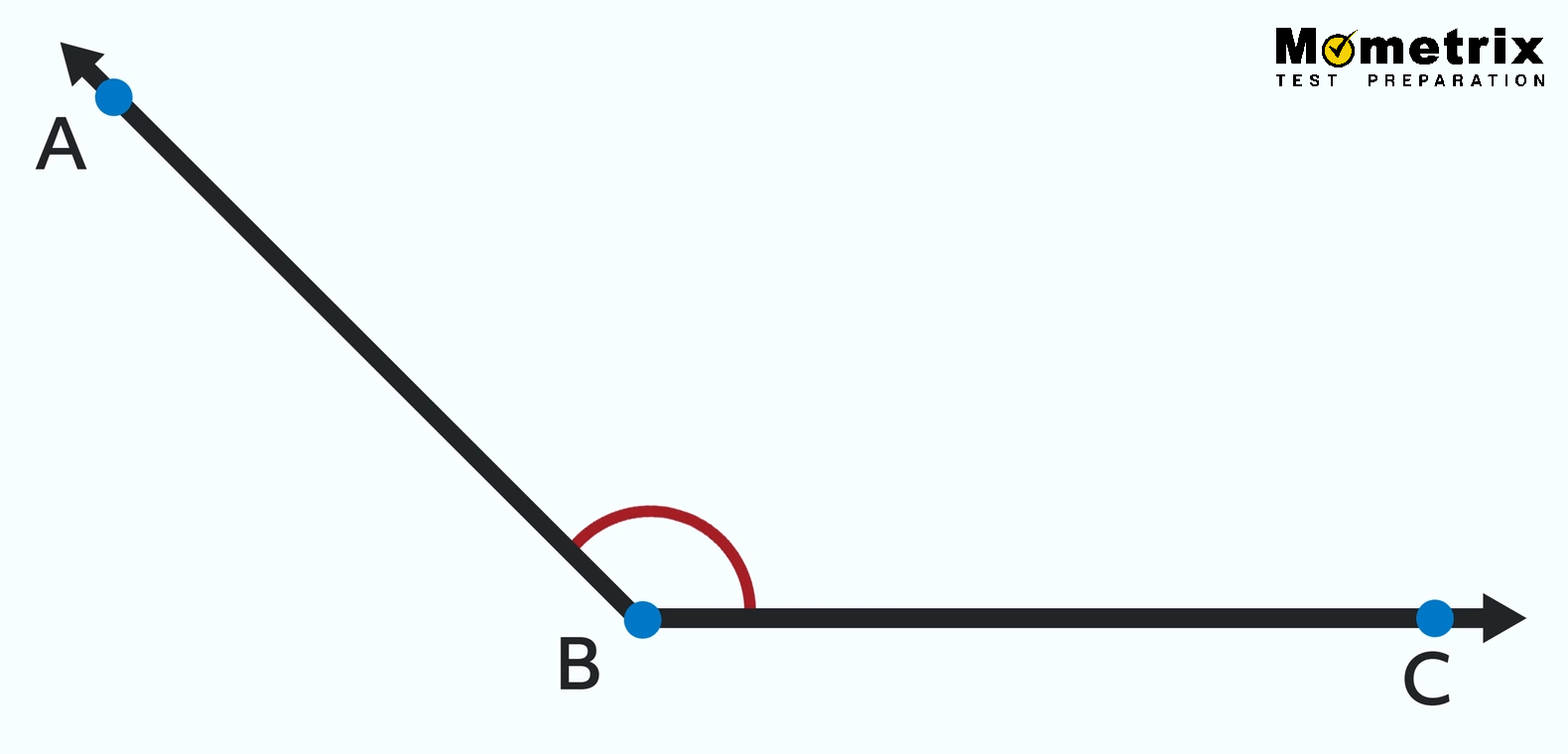
We can see that ∠ABC is an obtuse angle, which means it’s more than 90° and less than 180°. But what about the other side?
This is called a reflex angle.
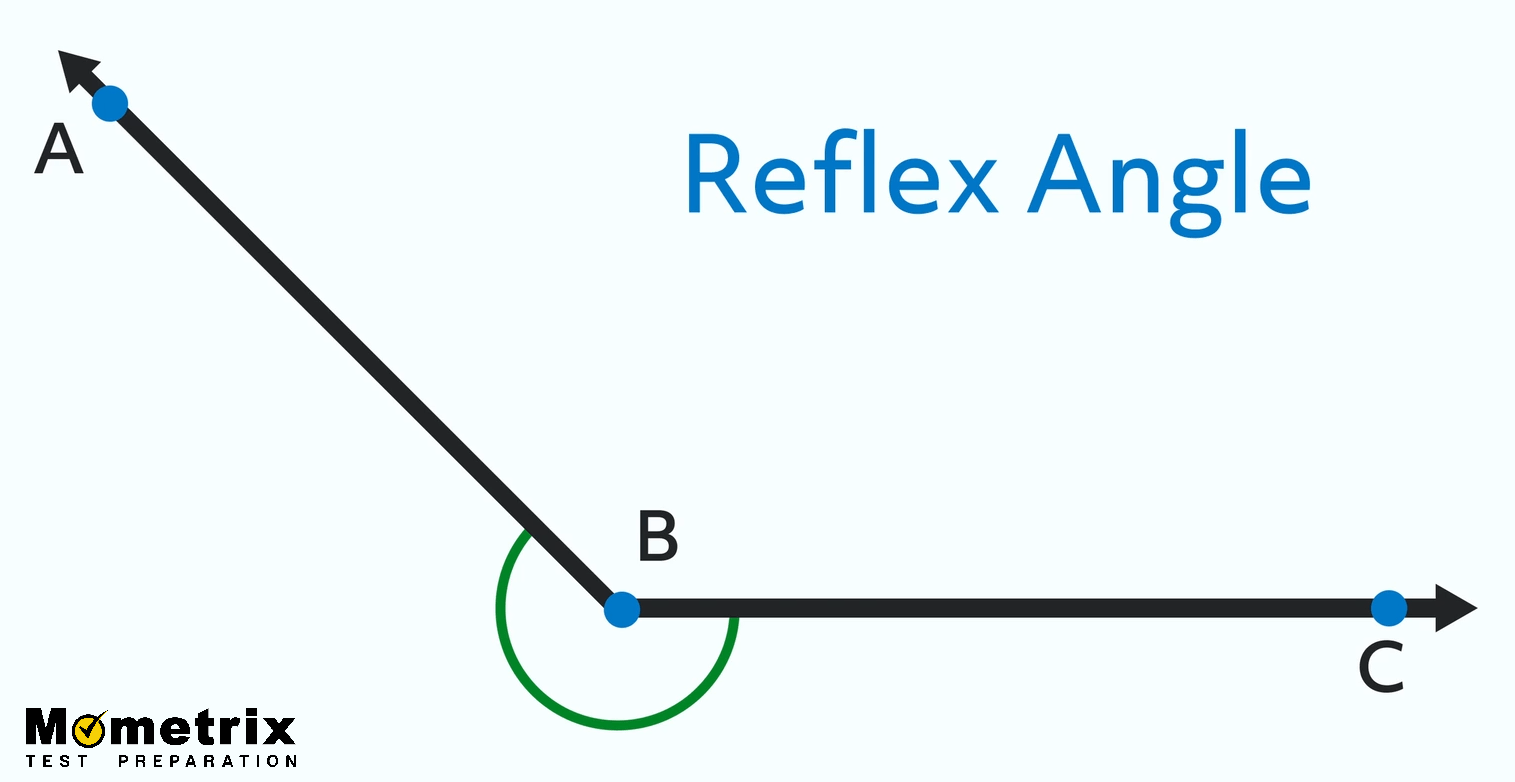
It’s always more than 180° and less than 360°. Every acute, right, and obtuse angle has a reflex angle.
Example Problems
Next, let’s take a look at where we’ll see some of these angles in the wild, or at least in geometry problems.
Let’s start by looking at two lines that intersect. In this case, we’ve numbered the angles.
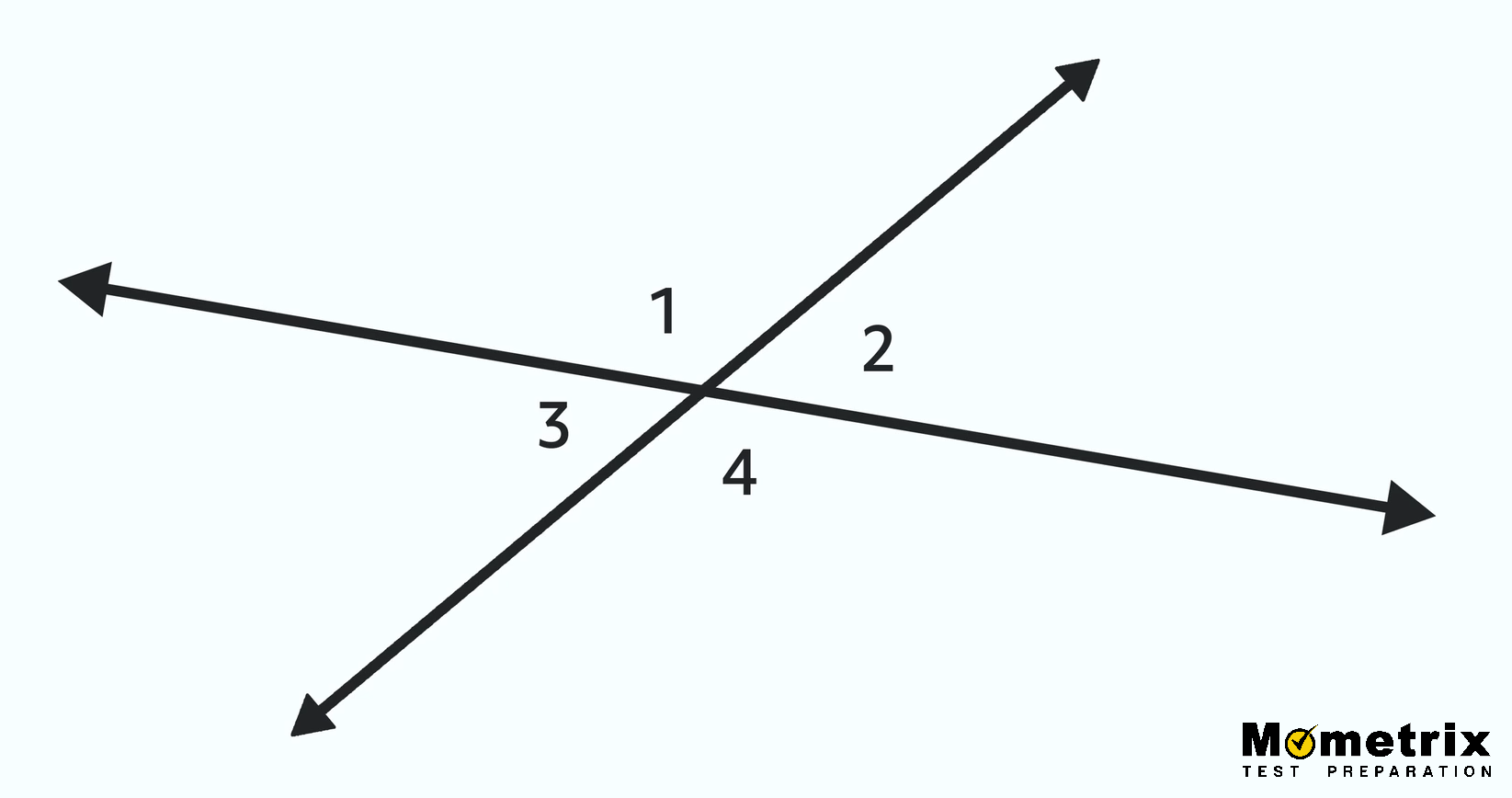
Whenever we see a figure like this, if we know any of the angles we can determine all of the others! So if ∠1 measures 130°, we can figure out ∠2 because those two angles together form a line and are a linear pair and supplementary. So ∠2 must be 50°. The same works for angles 1 and 3. And then we can use what we know about ∠2 to pair it up with ∠4 to find that angle. When it’s all said and done it looks like this:
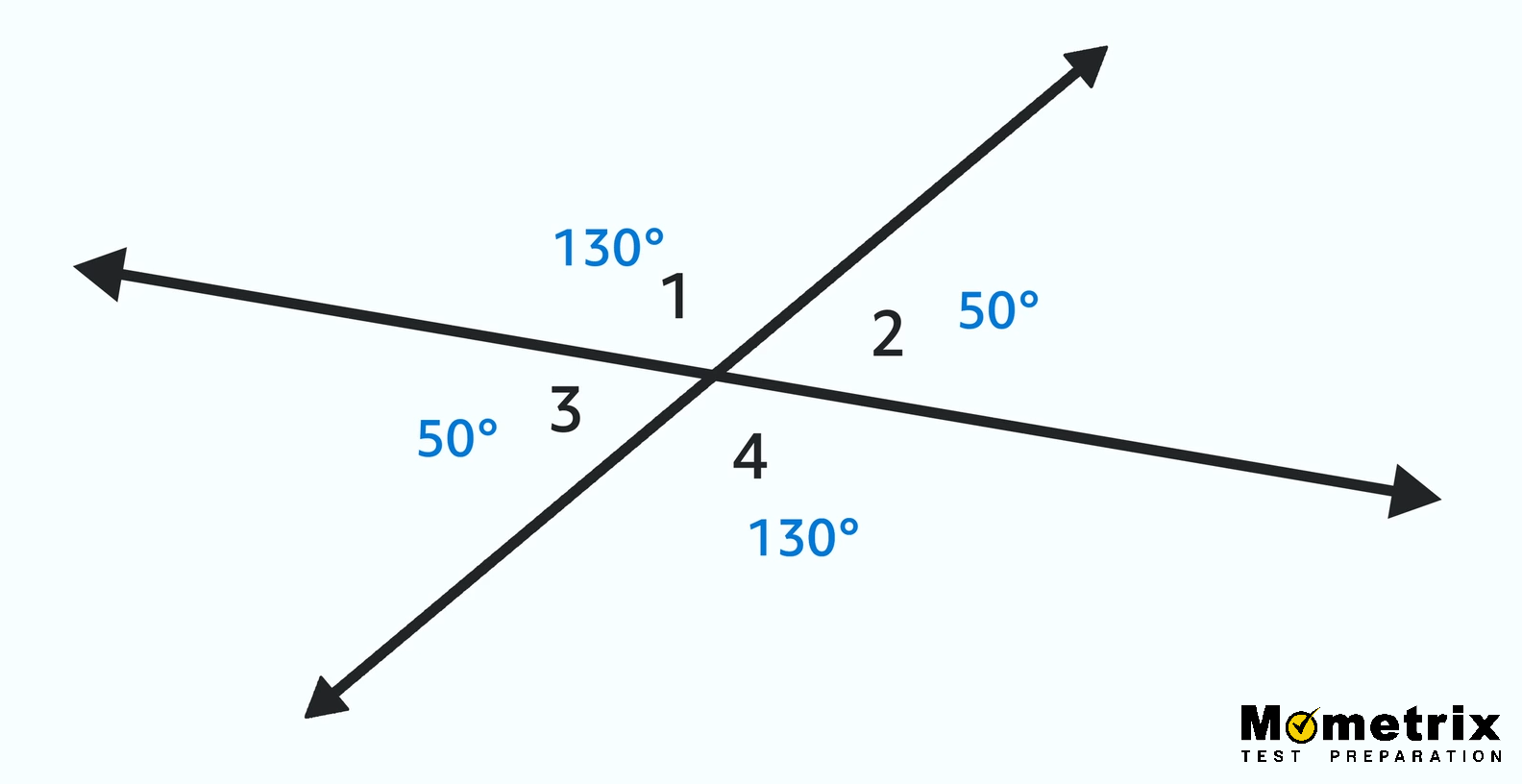
Notice that the angles opposite one another have the same measure. These angles are called vertical angles, and they’re always congruent, which is geometry-speak for having the same measure.
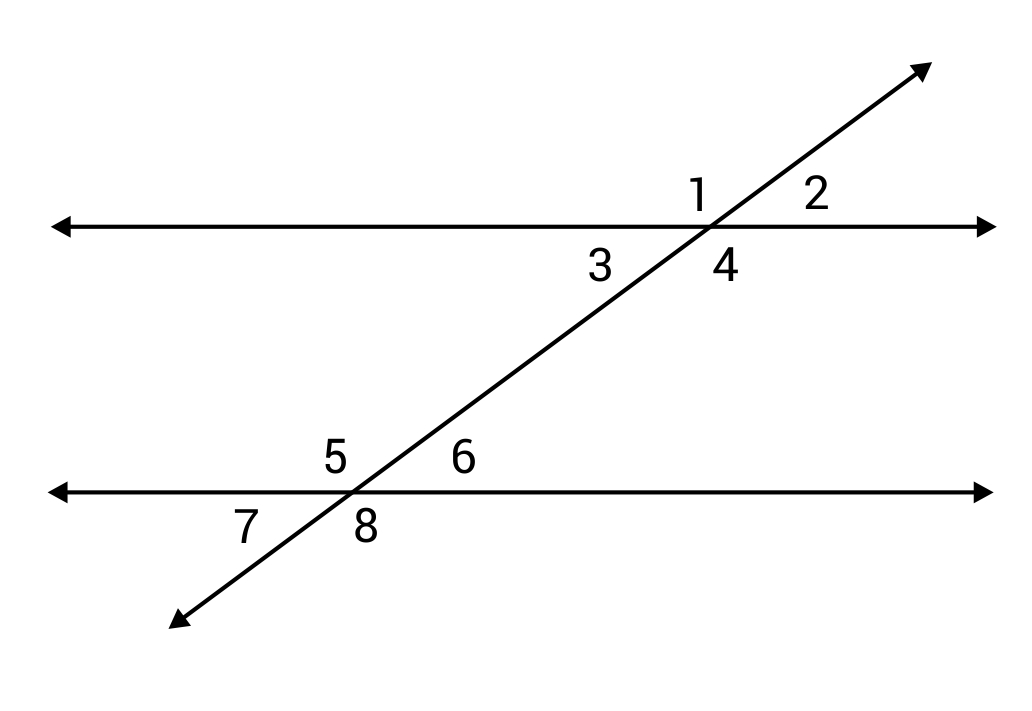
Now let’s look at three lines intersecting:
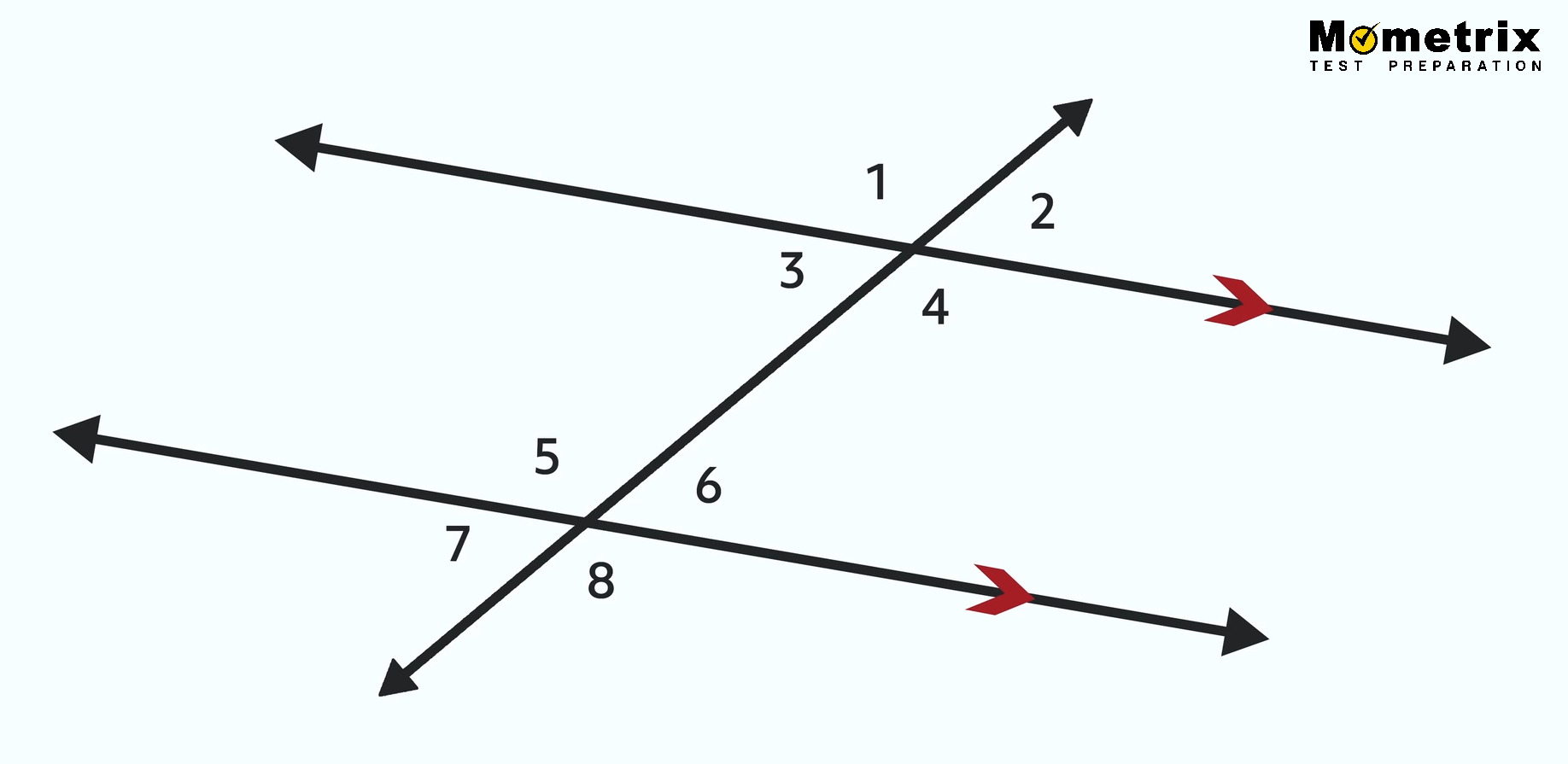
This is called a transversal. Once again we’ve numbered the angles, and there are red arrow marks on two of the lines, indicating that they are parallel. A transversal doesn’t have to have parallel lines but when it is, it allows us to know a lot about the eight angles created by the intersecting lines.
But before we get to that, let’s look at the eight angles. We can see they are in two groups of four (angles 1-4 and 5-8). Angle 1 is in the top-left position in the top group of angles. If we look at the same spot in the bottom group of angles we see that ∠5 is in the top-left spot for that group. That means that ∠1 and ∠5 are corresponding angles. So ∠2 and ∠6 are also corresponding angles because they’re in the top right spot for their respective groups. ∠3 and ∠7 are also corresponding, as are ∠4 and ∠8. In a transversal, when there’s a pair of parallel lines, corresponding angles are congruent. When the lines are not parallel, the corresponding angles are not congruent.
In the case of our diagram that does have parallel lines, if we know that ∠2 is 55° we then know that ∠6 is also 55°. And once we know that, we can use what we learned about vertical angles and linear pairs to find all the others:
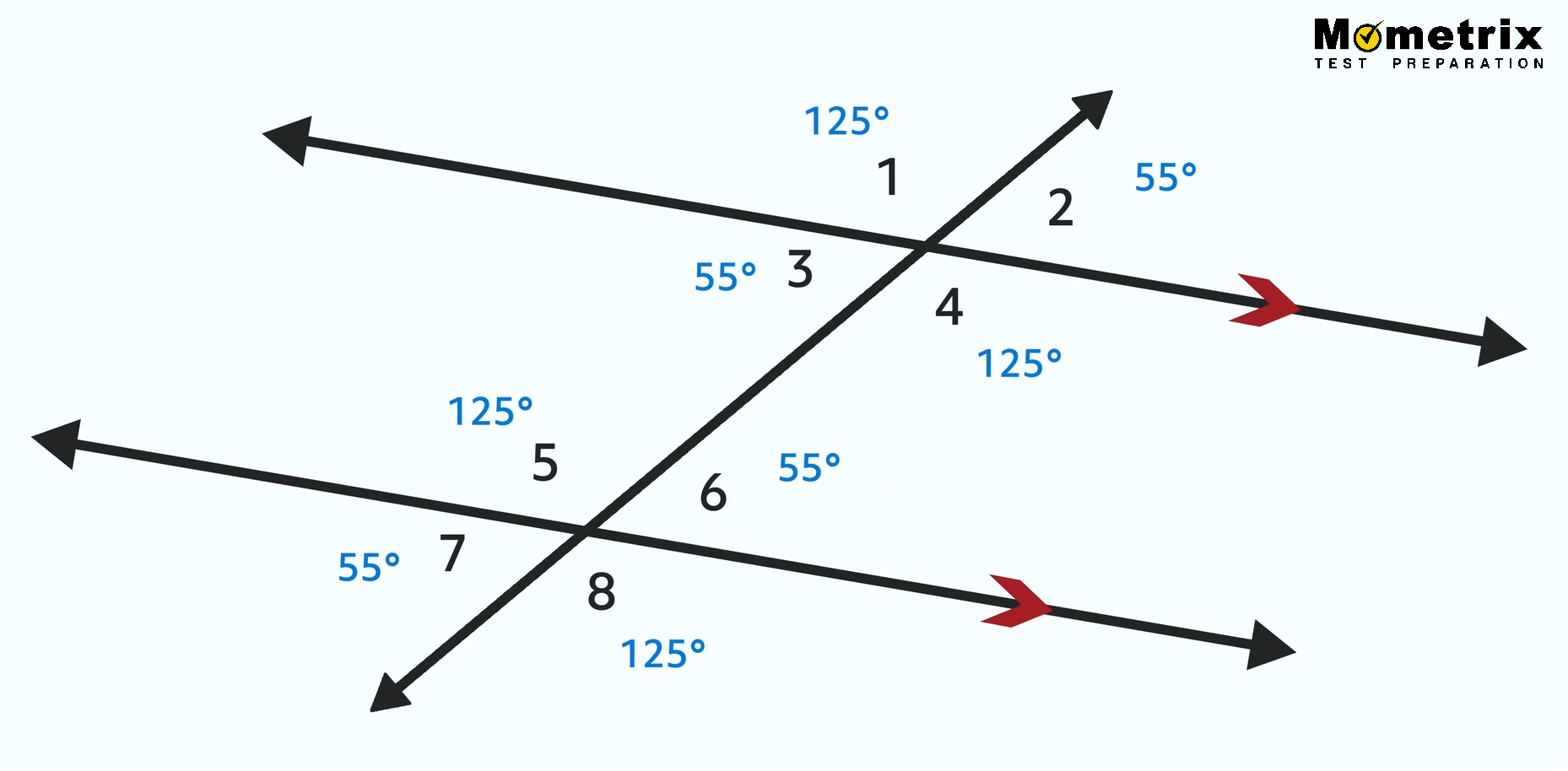
That’s all we need to know to find our angles, but there is some more location-based vocabulary we need to be aware of with these types of problems. Interior angles are the angles between the parallel lines. In this case, that’s ∠3, ∠4, ∠5, and ∠6. The exterior angles are the ones that, you guessed it, are not between the parallel lines. So ∠1, ∠2, ∠7, and ∠8 are exterior angles.
Alternate angles are angles that are on opposite sides of the line that cuts across the parallel lines. And same-side angles are angles that are on the same side of that line, of course.
In questions about the two groups of angles, this is used to combine interior or exterior with alternate or same side angles. The question will always relate to the other group of angles. Something like “what is the alternate interior angle for ∠3?” We would look to the other group of angles, then to the other side of the intersecting line, and then find the only angle that is an interior angle, which would be ∠6. The same side interior angle for ∠3 is ∠5.
Review
That’s a lot to absorb in a small amount of time. Referencing the image above, try these questions to see if it has sunk in:
1. What is the alternate exterior angle to ∠8?
2. What is the same side exterior angle to ∠7?
3. What is the corresponding angle to ∠5?
Thanks for watching, and happy angling!
Frequently Asked Questions
Q
What are complementary angles?
A
Complementary angles are two angles whose measures add up to 90 degrees.
Q
What is a supplementary angle?
A
A supplementary angle is an angle that adds to another angle to equal 180°.
Ex. What is the angle supplementary to a 107° angle?
180 – 107 = 73°
Q
What are vertical angles?
A
Vertical angles are pairs of angles opposite one another. One vertical angle always equals the other vertical angle.
Ex.
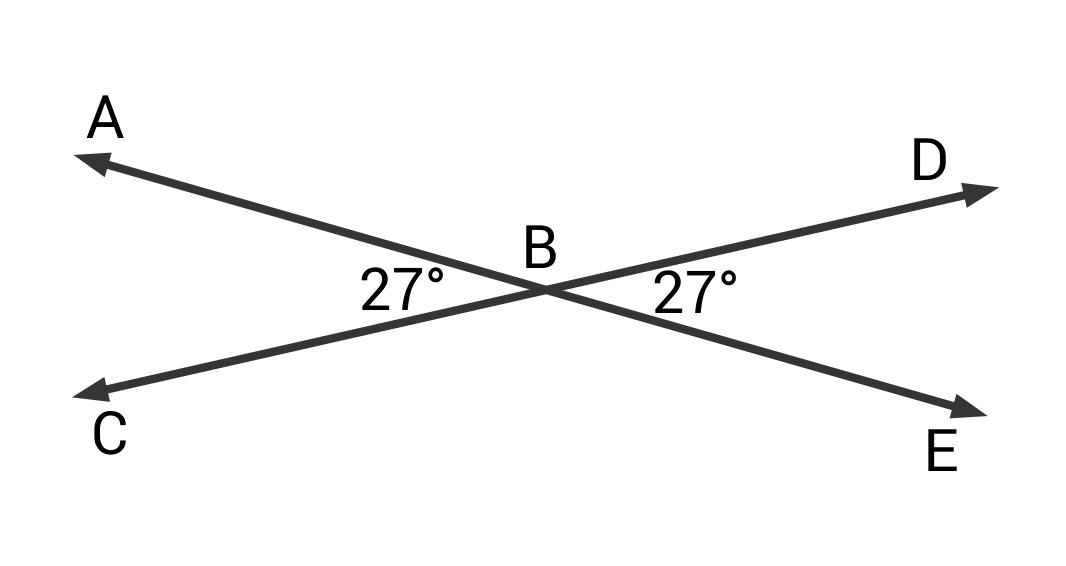
∠ABC and ∠DBE are vertical angles.
Q
What are corresponding angles?
A
Corresponding angles are angles that are in the same position relative to the transversal and a parallel line when two lines are cut by a transversal. Corresponding angles always have the same measure.
Ex.
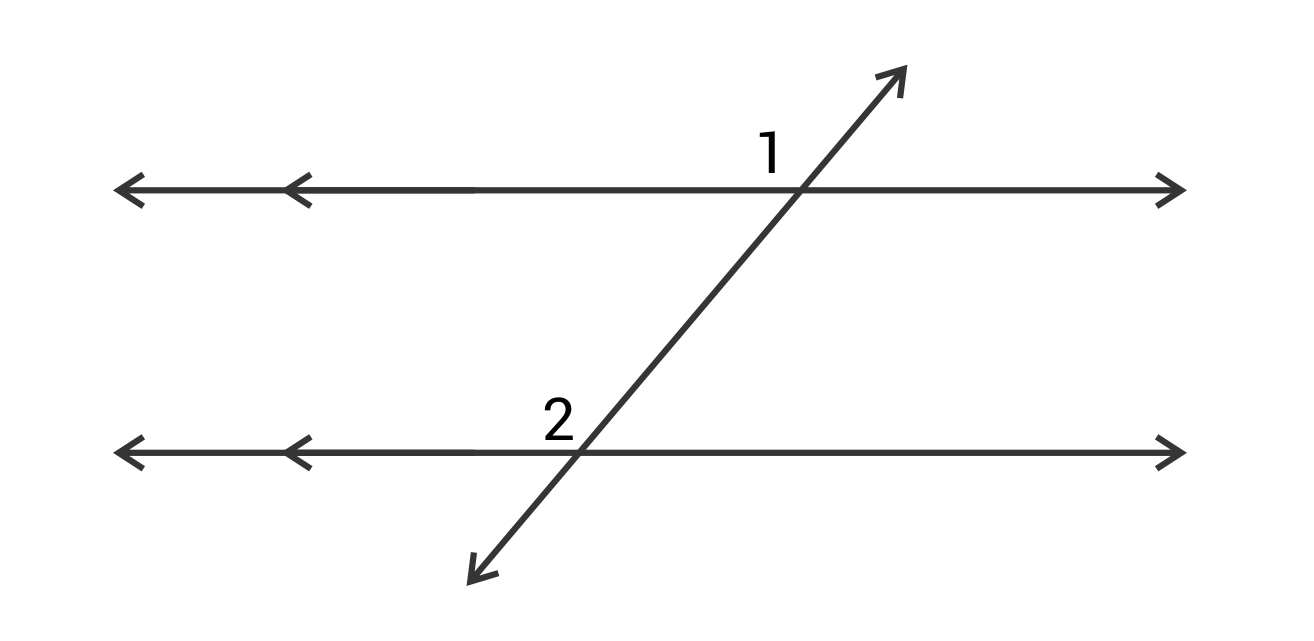
∠1 and ∠2 are corresponding angles.
Q
What is an acute angle?
A
An acute angle is an angle whose measure is less than 90 degrees.
Q
How do you find the angle of a triangle?
A
Find the angle of a right triangle by using the formulas: \(sinθ=\frac{opposite}{hypotenuse}\),\(cosθ=\frac{adjacent}{hypotenuse}\),and \(tanθ=\frac{opposite}{adjacent}\). These formulas can be remembered using the pneumonic SOH-CAH-TOA. Fill in the given side lengths and work backwards to solve for the angle (ϴ).
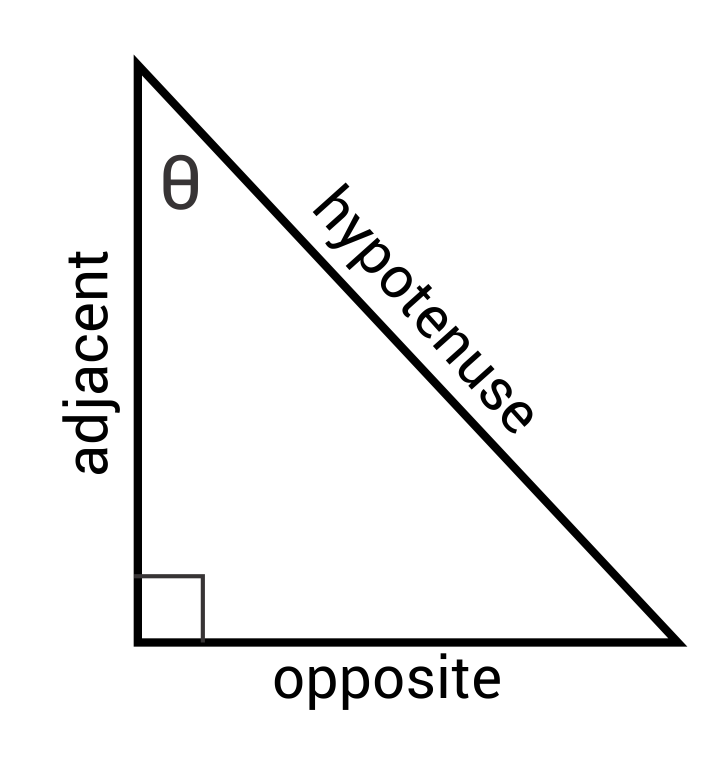
Ex. Find the value of ϴ.
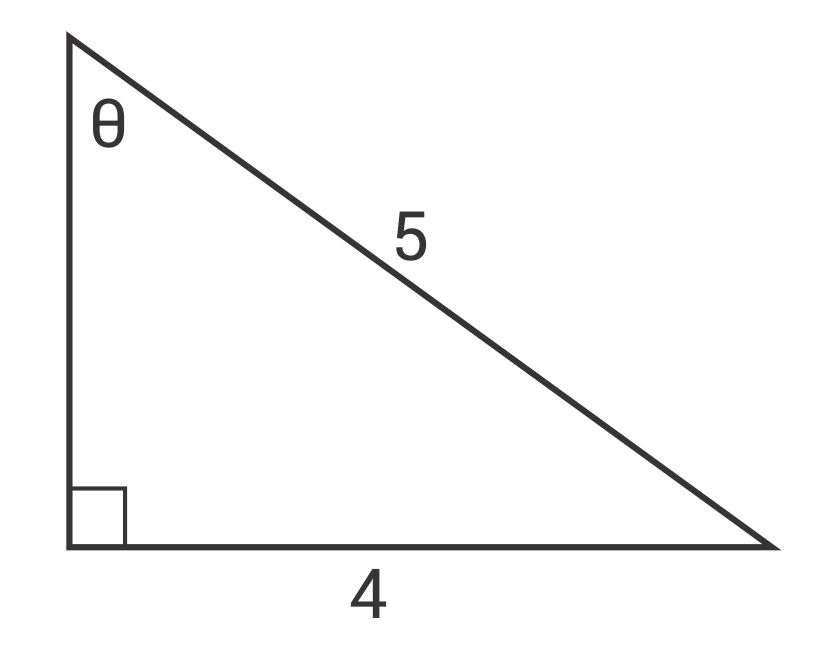
You are given the opposite and hypotenuse, so use the formula:
\(sinθ=\frac{opposite}{hypotenuse}\)
Fill in your given values.
\(sinθ=\frac{4}{5}\)
Work backwards to solve for ϴ.
\(θ=sin^{-1}\frac{4}{5}\)
\(θ≈53.13°\)
Q
What is an obtuse angle?
A
An obtuse angle is any angle that measures greater than 90°.
Ex.
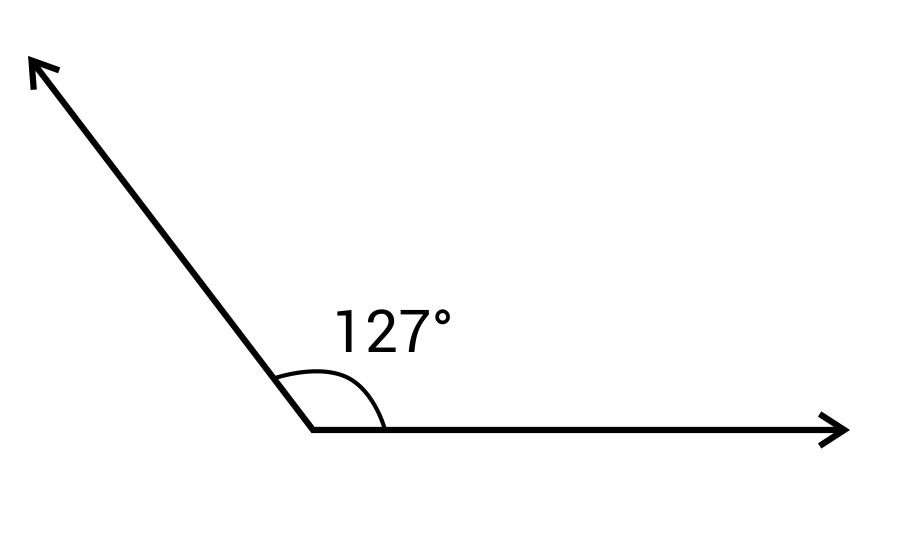
Angle Practice Questions
Which angle description matches the angle below?
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees.
Solve for x.
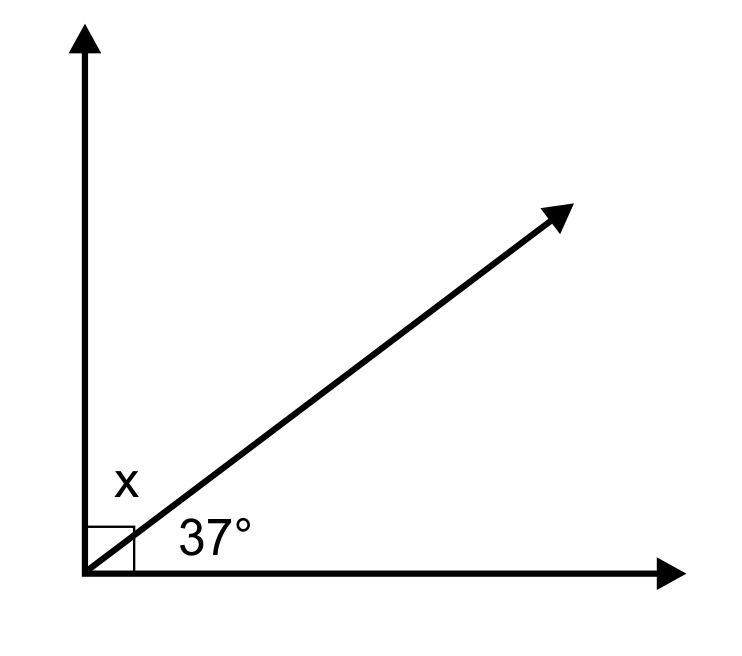
The sum of x and 37° will be 90° because these two angles are complementary. x can be calculated by subtracting 37 from 90. Either way, \(x=53°\).
Which angle pair would be considered vertical angles?
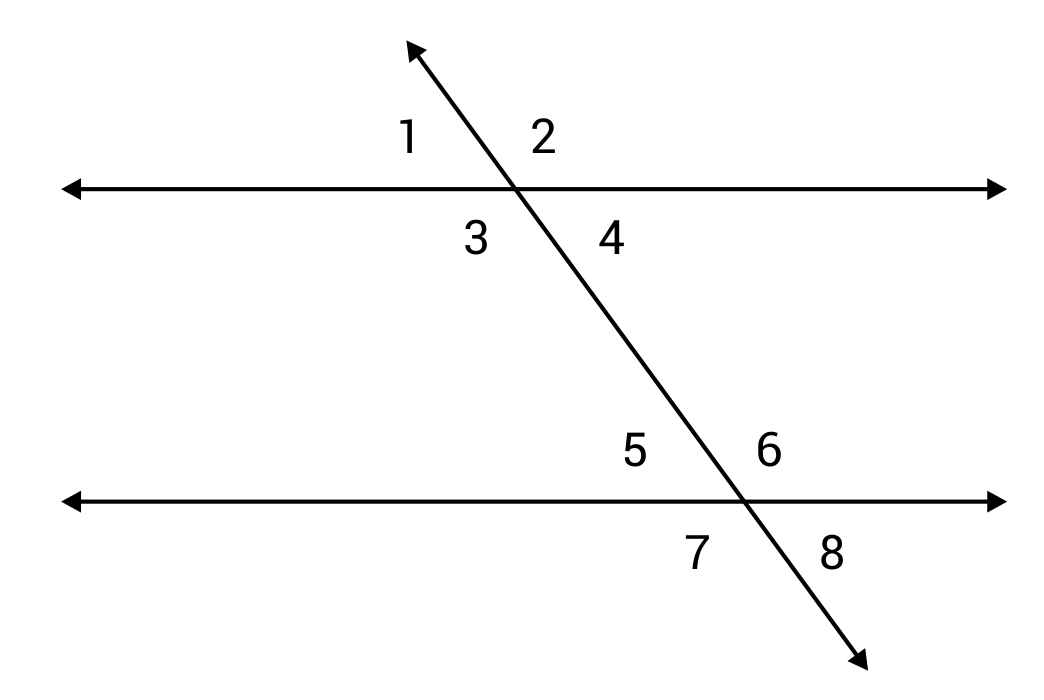
Vertical angles are also known as opposite angles. Opposite angles, or vertical angles, in the diagram include: 1 and 4, 2 and 3, 5 and 8, and 6 and 7.
Max sets up a sprinkler so that it sprays a 90° section of his lawn. He plans on rotating the sprinkler every 15 minutes so that the entire lawn receives water. How many times will the sprinkler need to be rotated so that the entire lawn is watered?

Each time the sprinkler is set up it waters one quarter of the entire lawn. This means that the sprinkler needs to be rotated four times in order to reach each section. \(90°×4\text{ sections}=360°\) (the total yard).
A walking path crosses over a set of train tracks creating a transversal line. If the measure of Angle 1 is 120 degrees, what is the measure of Angle 3?
Angles 1 and 3 are supplementary angles. The sum of Angles 1 and 3 will be 180 degrees. If Angle 1 is 120 degrees, then \(180-120\) gives us the value of Angle 3. Angle 3 is 60 degrees.