
Hi, and welcome to this video on the perimeter and area of a triangle!
To get started, let’s quickly review what perimeter and area measure. Imagine we have a triangular-shaped yard.

If we wanted to build a fence around our yard, we’d need to know the distance around the yard. This is the perimeter. If we wanted to buy sod for our yard, we’d need to know the area of the yard so that we can buy the correct amount.
And while it might be a bit unusual to have a yard that is the shape of a triangle, you might have a part of a yard that you want to fence or sod shaped like a triangle.
How to find the Perimeter of a Triangle
Okay, now that we know what perimeter and area are, let’s figure out how to find the perimeter. We don’t need a fancy formula or anything. All we need to do is add the length of the sides together. So if we know all the sides of our yard we can easily find the perimeter:

\(20m+20m+12m=52m\) of fence. Not much to that one. Notice that the answer is given in meters. That’s because perimeter is a distance. Walking around the yard would mean walking 52 meters.
That’s all there is to it, no matter what type of triangle you have. Just add up the length of the sides and you have your perimeter.
How to find the Area of a Triangle
Now let’s deal with area. There’s an actual formula for finding the area of a triangle, which is \(A= \frac{1}{2}bh\)
Let’s quickly explain where that \(\frac{1}{2}\) came from. The formula for the area of a parallelogram is \(A=bh\). If we compare the two shapes, we can see that a parallelogram can be made by two equal-sized triangles:
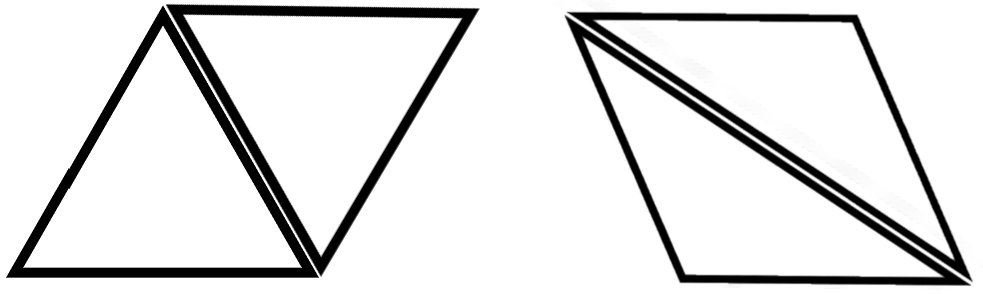
So we can say a triangle is half a parallelogram, which is where the one half comes from in the formula.
For triangles, the formula for area does work a bit differently depending on the type of triangle. Let’s start with right triangles.
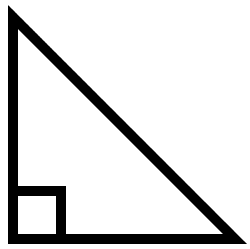
We have our formula, but the question we need to answer is which side is \(b\) and which side is \(h\)?
For a right triangle like this one, \(b\) and \(h\) are the two sides adjacent, or next to, the right angle. It doesn’t matter which is which, so let’s say that \(b=6\) cm and \(h=8\) cm.
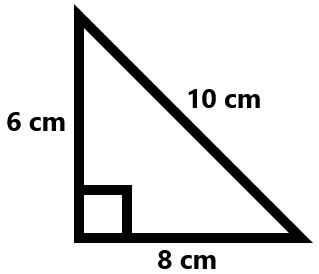
Now we can plug them into our formula:
It’s always a good idea to substitute with parentheses to help keep things organized. We’ve even left the units in so that we can see what will happen with them. At this point, we only have multiplication left to do, so according to the commutative property of multiplication, we can rearrange before multiplying:
Now let’s solve this:
\(3\times 8=24\)
\(\text{cm} \times \text{cm}= \text{cm}^2\)
So, we end up with our area as 24 cm\(^2\).
For area problems, the answer will always be in square units. That’s because we’re trying to determine how many square centimeters will fit in our triangle. We can see that clearly by looking at an isosceles right triangle that has legs measuring 5 units on some graph paper:
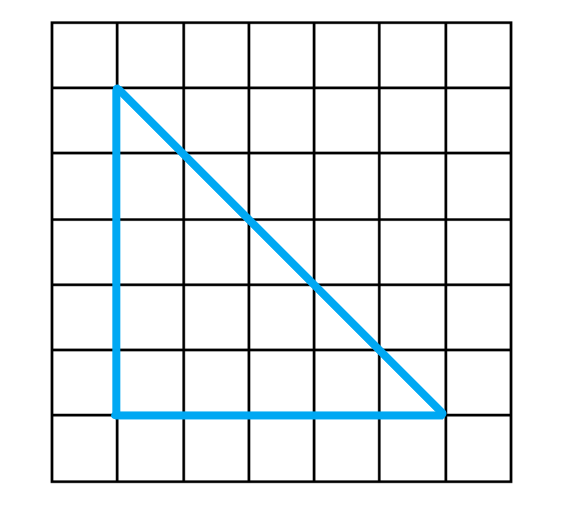
How many squares are inside the triangle? We can count them. First, we’ll count the whole squares that fit inside, then we’ll add the half squares:
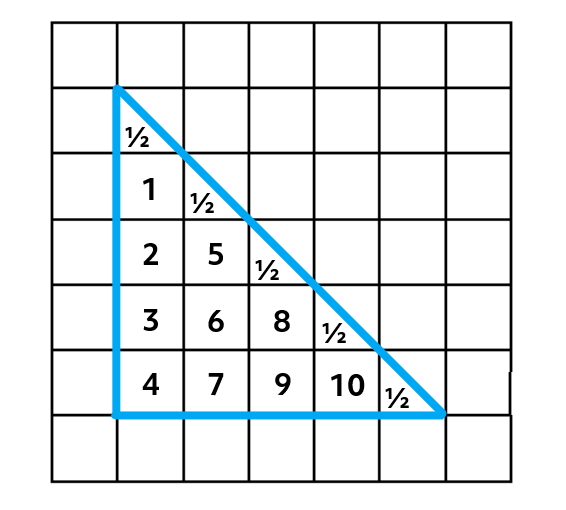
There are 10 full squares plus 5 half squares for a total of 12\(\frac{1}{2}\) squares.
If we use our formula we’ll find the same thing:
\(A=\frac{1}{2}(25)\)
\(A=12.5\)
Now we’ve seen the formula work and gained a better understanding of why the units are squared. All we have left to do is find the area of acute and obtuse triangles.
Let’s start with an acute triangle:
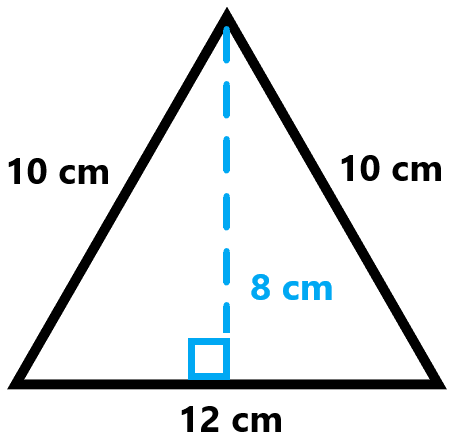
Note that the height is always perpendicular to the base. From here we can find the area:
\(A=\frac{1}{2}(96)\)
\(A=48\text{ cm}^2\)
The same thing applies to obtuse triangles, except the height or altitude will often appear outside of the triangle, like this:
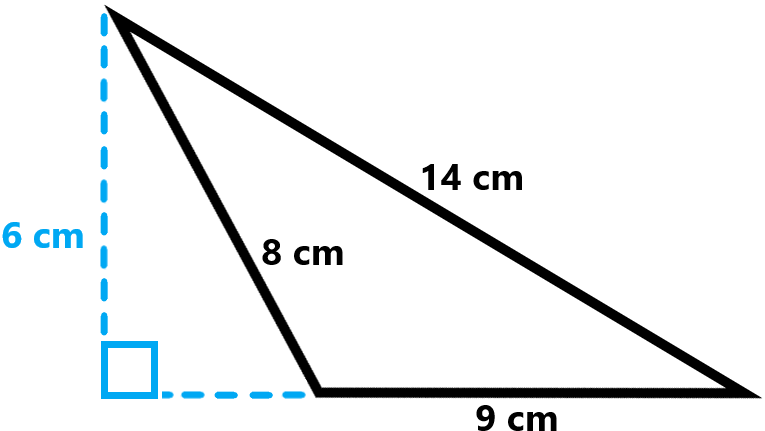
We can see that the height of the triangle is 6 cm, and the side it is perpendicular to is the base, which measures 9 cm. We don’t need the other two numbers at all. Let’s plug in the base and height:
\(A=\frac{1}{2}(54)\)
\(A=27 \text{ cm}^2\)
That’s all there is to it! Here is one more for you to solve on your own. Try pausing this video and then finding the perimeter and area of this triangle.
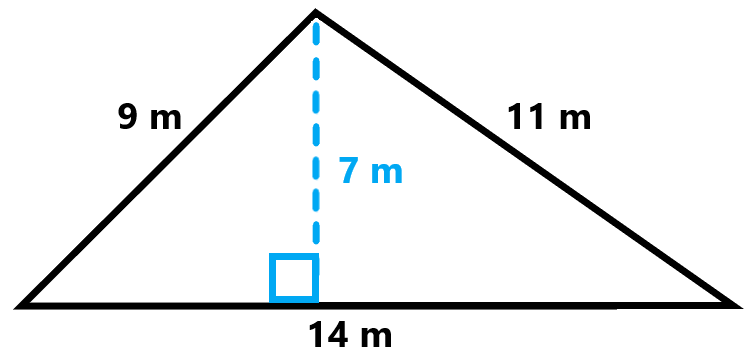
Think you got it? The perimeter is 34 m and the area is 49 m\(^2\).
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you find the area of a triangle?
A
Find the area of a triangle by multiplying its base times its height and dividing by two.
\(A=\frac{1}{2} bh\)
Ex. What is the area of this triangle: 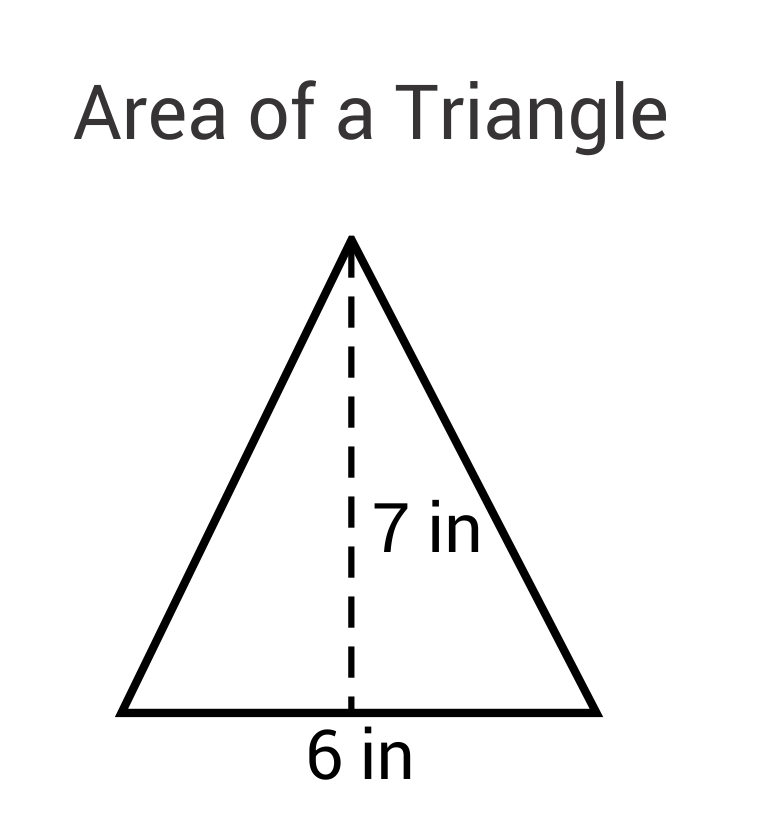
\(A=\frac{1}{2} bh=\frac{1}{2} (6)(7)=21in^2\)
Q
How do you find the perimeter of a triangle?
A
Find the perimeter of a triangle by adding the lengths of all three sides together.
Ex. What is the perimeter of this triangle?
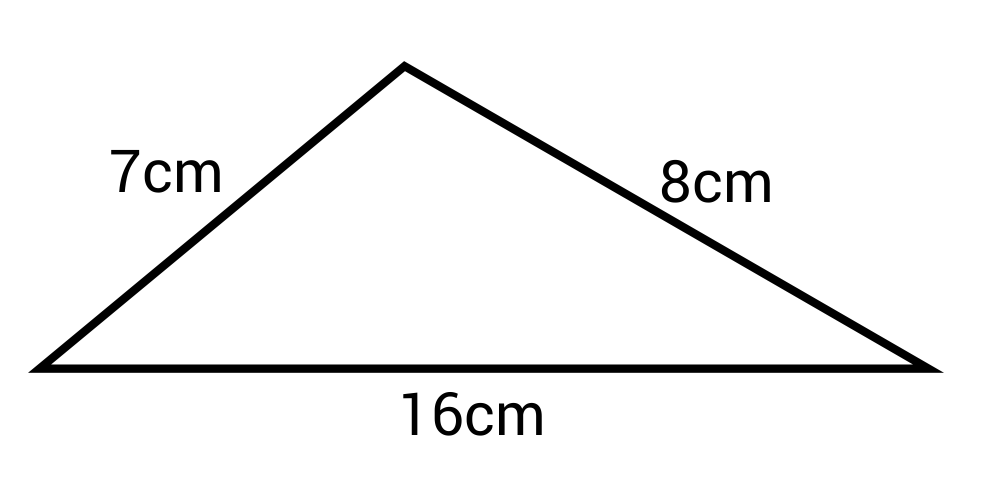
P = 7 + 8 + 16 = 31 cm
Q
How do you find the area of a right triangle?
A
Find the area of a right triangle by multiplying its base times its height and dividing by 2.
\(A=\frac{1}{2} bh\)
Ex. What is the area of this right triangle?
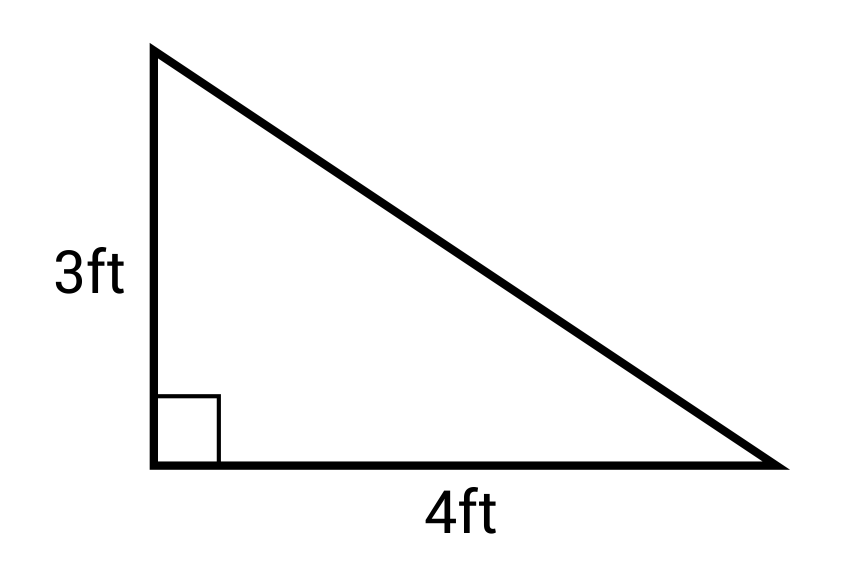
\(A=\frac{1}{2} bh=\frac{1}{2} (3)(4)=6 ft^2\)
Q
How do you find the perimter of a right triangle?
A
Find the perimeter of a right triangle by adding the measures of all three sides together.
Area and Perimeter of a Triangle Practice Questions
What is the perimeter of this triangle?
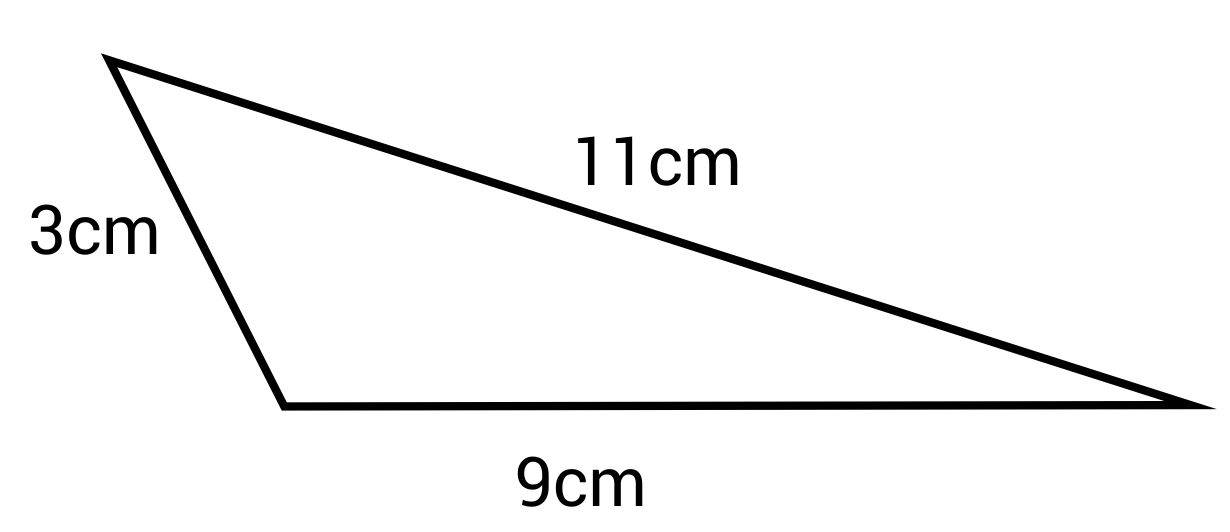
The correct answer is 23 cm. To find the perimeter of a polygon, add the lengths of all the sides together.
\(P=3+11+9=23\text{ cm}\)
What is the area of this triangle?
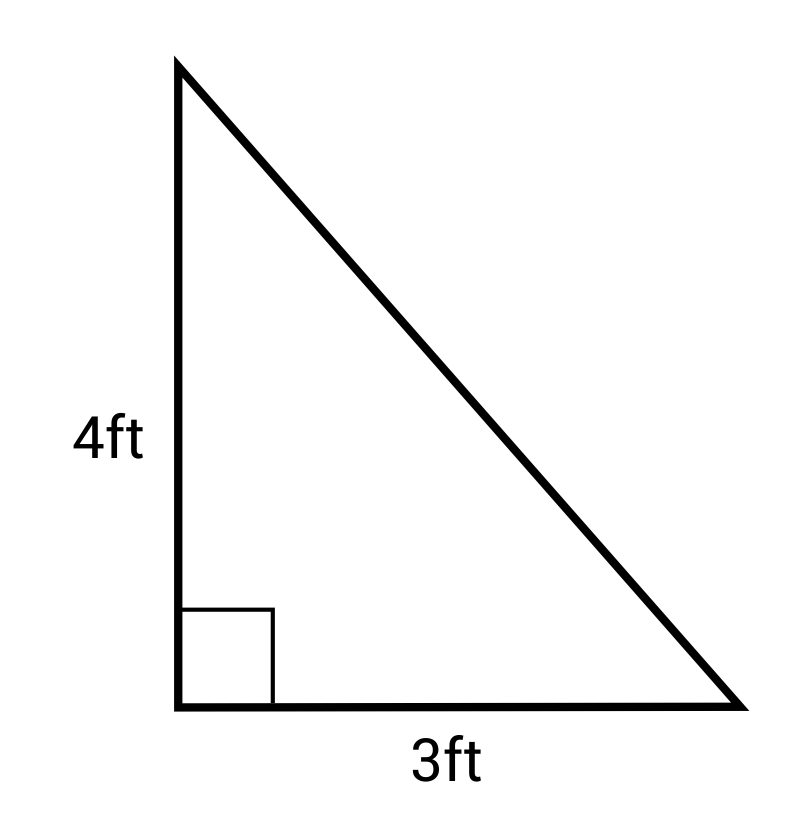
The correct answer is 6 ft2. To find the area of a triangle, use this formula:
\(A=\frac{1}{2}bh\)
The base (b) is 3 ft and the height (h) is 4 ft.
\(A=\frac{1}{2}(3)(4)=6\text{ ft}^2\)
What is the formula for perimeter of any triangle?
The correct answer is \(P=a+b+c\). To find the perimeter of a polygon, add together the lengths of each side, \(P=a+b+c\). \(P=3s\) can only be used for equilateral triangles, not all triangles. And \(P=2a+b\) can only be used for isosceles triangles.
What is the area of this triangle?
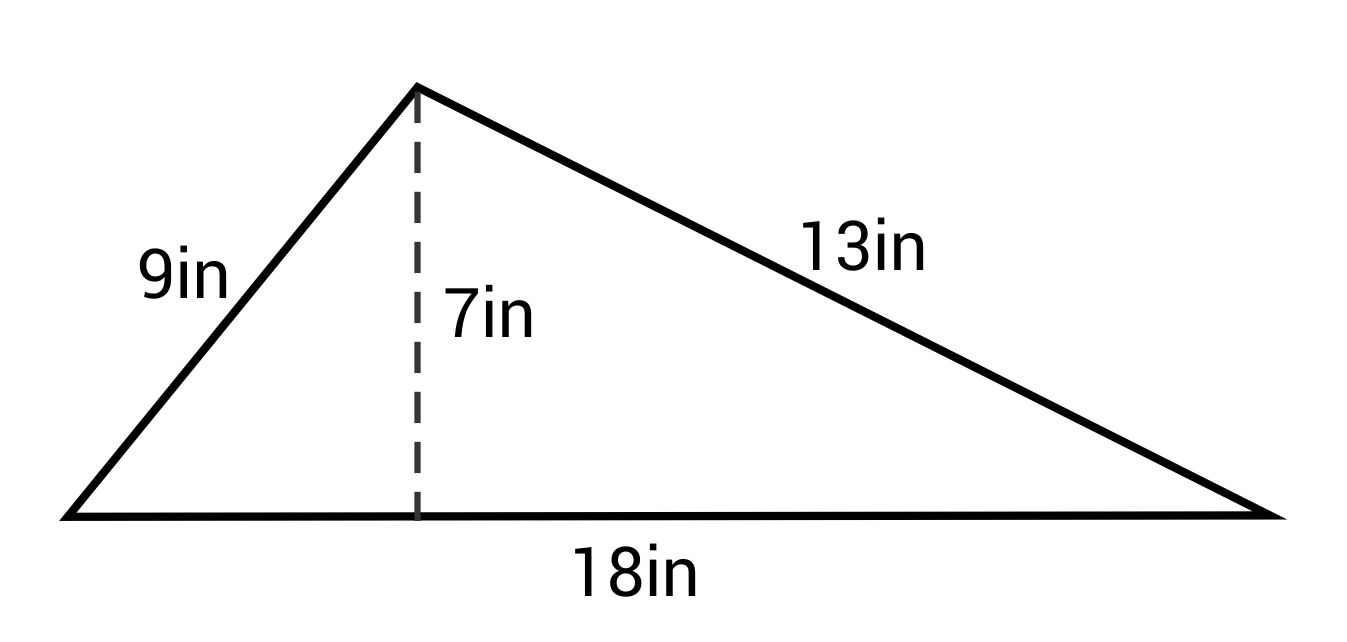
The correct answer is 63 in2. The formula for area of a triangle is:
\(A=\frac{1}{2}bh\)
The base (b) is 18 in and the height (h) is 7 in.
\(A=\frac{1}{2}(18)(7)=63\text{ in}^2\)
What is the perimeter of this isosceles triangle?
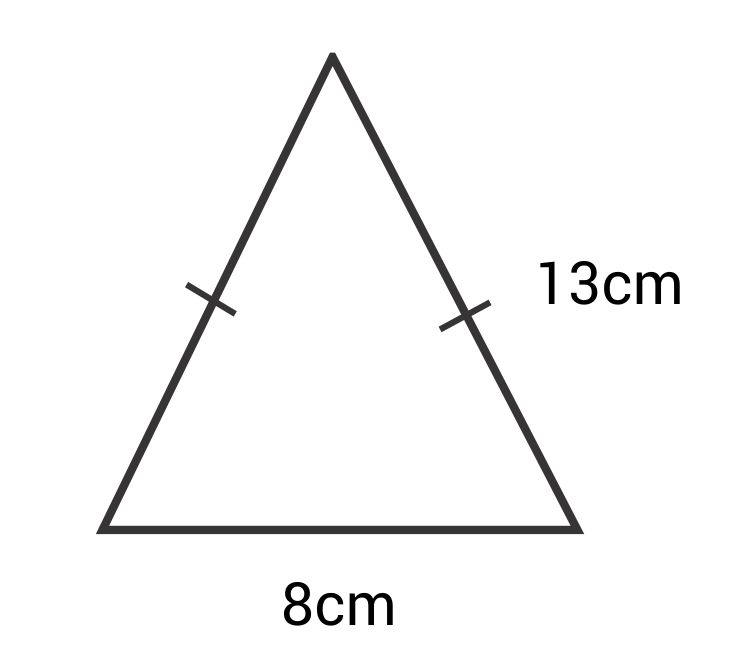
The correct answer is 34 cm. To find the perimeter of a polygon, add the lengths of all the sides together. Since this is an isosceles triangle, two of the sides measure 13 cm.
\(P=13+13+8=34\text{ cm}\)