
Congruent Angle Overview
Congruent angles are frequently used in the world of architecture, construction, design, and art. Congruent angles have the same angle measure. For example, a regular pentagon has five sides and five angles, and each angle is 108 degrees. Regardless of the size or scale of a regular polygon, the angles will always be congruent.
There are many rules that allow us to determine whether angles are congruent or not. For example, if two triangles are similar, their corresponding angles will be congruent. This means that the angles that are in the same matching position will have the same angle.
Another common test for angle congruence requires a set of parallel lines and a transversal line that slices through the set of parallel lines. For example, lines a and b are parallel, and line l is a transversal that slices through the parallel lines. When this situation occurs, a handful of congruent angles are formed.
There are four main types of congruent angles formed in this scenario: alternate interior angles, alternate exterior angles, corresponding angles, and vertical angles. 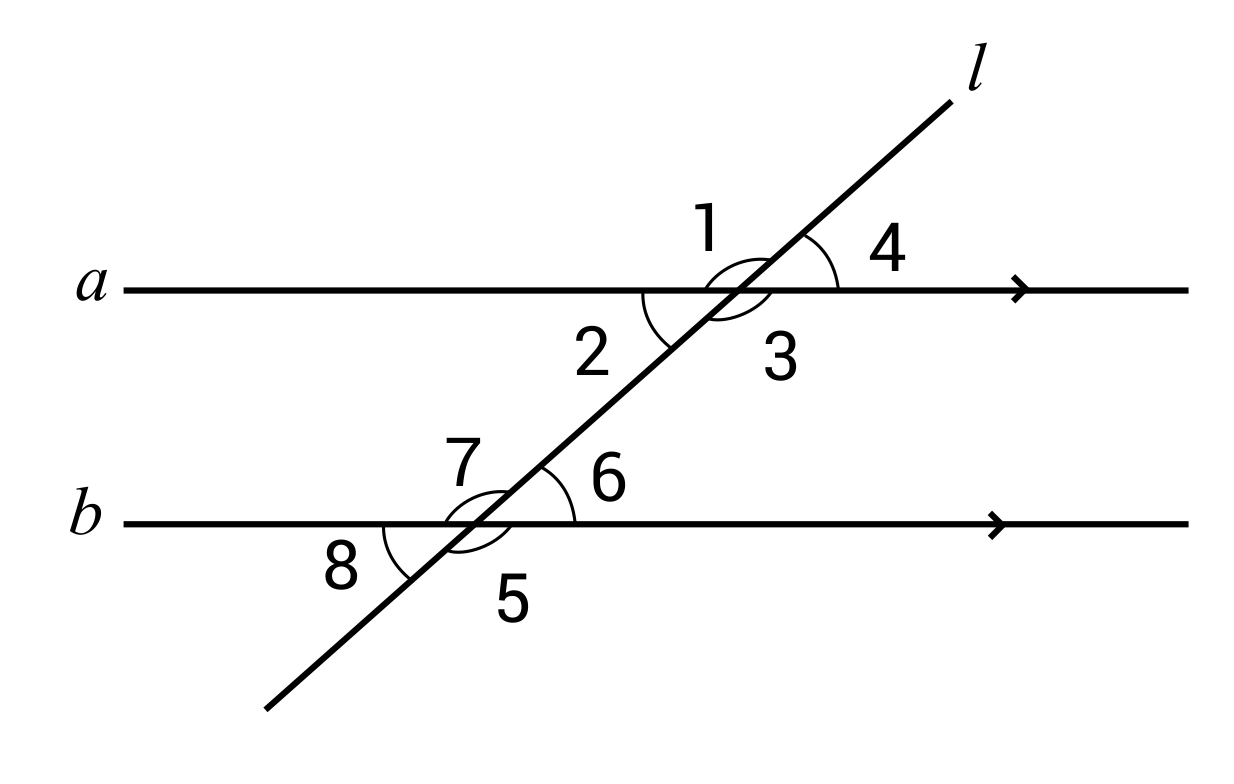
Alternate Interior Angles
Alternate interior angles are located in between the two parallel lines but on alternate sides of the transversal. For this particular example, the congruent alternate interior angles would be ∠2 and ∠6, and ∠7 and ∠3.
Alternate Exterior Angles
Similarly, alternate exterior angles are located on the outside of the parallel lines, and on alternate sides of the transversal. ∠5 and ∠1 are congruent, as well as ∠4 and ∠8.
Corresponding Angles
Corresponding angles are located on the same side of the transversal and in a similar matching location. For example, ∠4 and ∠6 are corresponding angles, therefore they are congruent. Other pairs of corresponding angles include ∠3 and ∠5, ∠1 and ∠7, and ∠2 and ∠8.
Vertical Angles
Vertical angles are formed by angles that are opposite of each other. For example, ∠1 and ∠3, ∠7 and ∠5, ∠4 and ∠2, ∠6 and ∠8 are all pairs of congruent angles. Vertical angles, or opposite angles, are commonly used as a proof of congruence.
Triangle Congruence
Another category of congruent angles revolves around triangle congruence. Triangle congruence rules are used to prove if two triangles are congruent or not. These rules take into consideration the side lengths and angles of triangles in order to determine congruence.
Four criteria are used to determine triangle congruence, and they are conveniently named. For example, S-S-S refers to two triangles that have all side lengths the same. If this is true, then all the corresponding angle measures will be congruent as well. 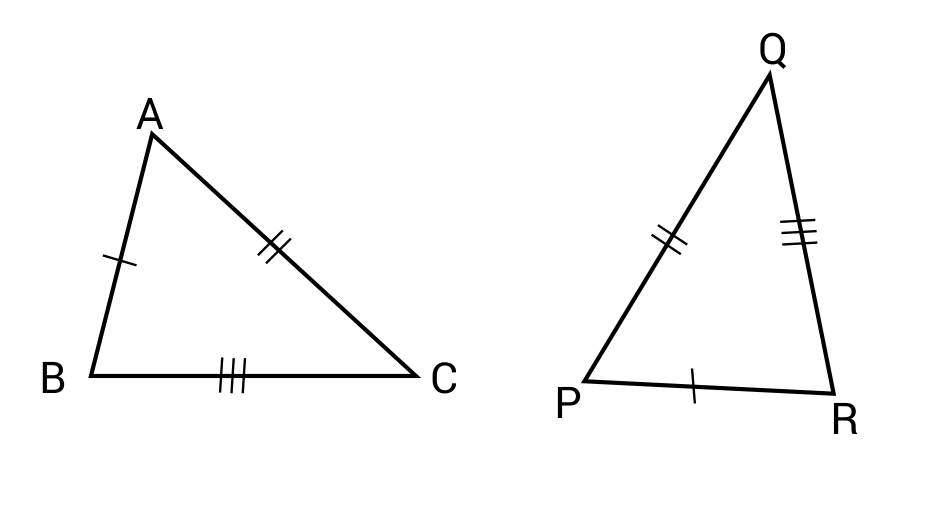 S-A-S refers to two triangles that have two congruent sides, with one congruent angle in between. If this is true, then all the corresponding angles will be congruent.
S-A-S refers to two triangles that have two congruent sides, with one congruent angle in between. If this is true, then all the corresponding angles will be congruent. 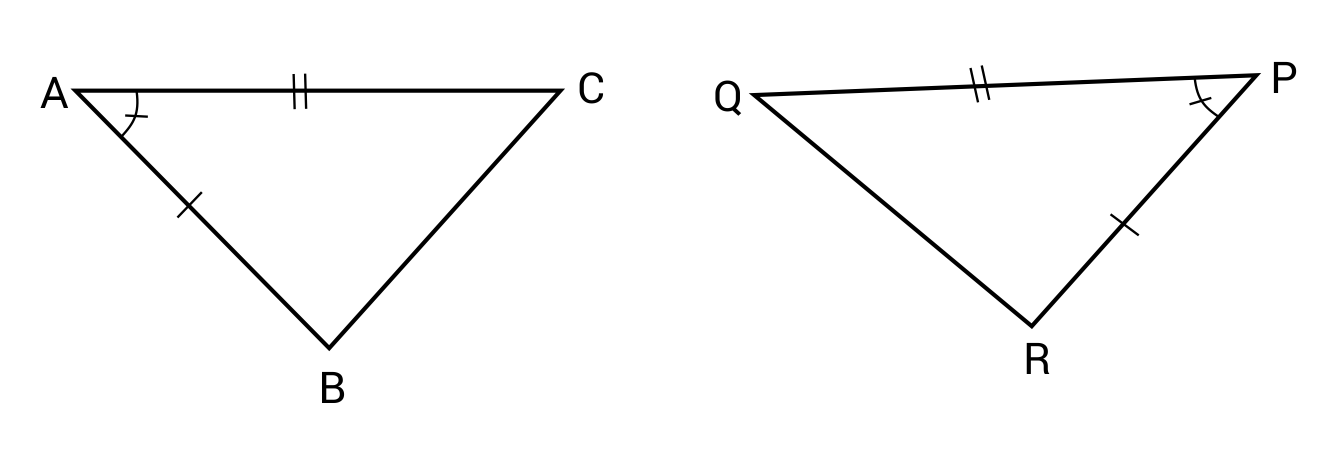 Similarly, A-S-A tells us that two triangles have two congruent angles, with one congruent side length in between. Again, if this is true, then all the corresponding angles will be congruent.
Similarly, A-S-A tells us that two triangles have two congruent angles, with one congruent side length in between. Again, if this is true, then all the corresponding angles will be congruent. 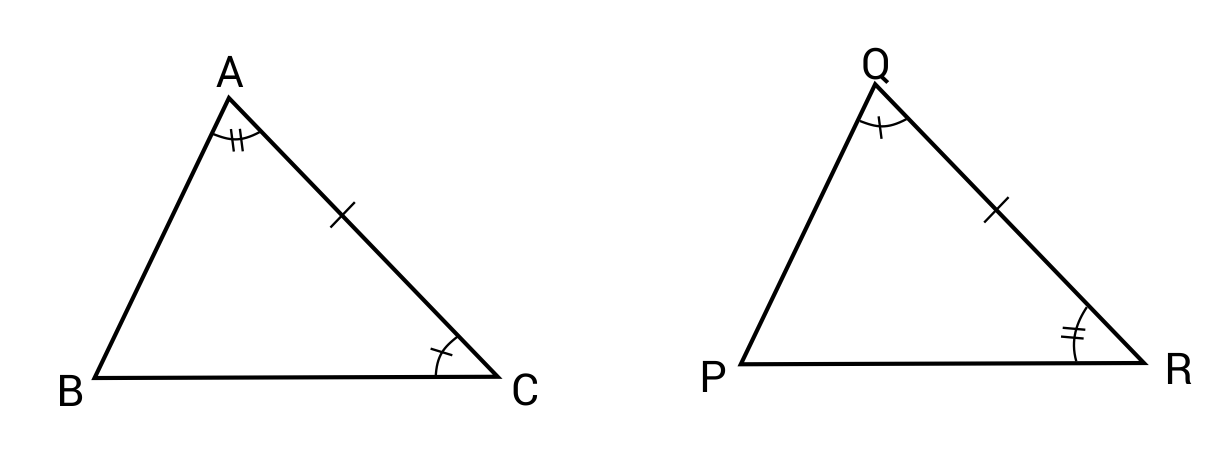 Lastly, A-A-S refers to two triangles that have two corresponding congruent angles, with a corresponding congruent side length. This tells us that all the corresponding angles will be congruent.
Lastly, A-A-S refers to two triangles that have two corresponding congruent angles, with a corresponding congruent side length. This tells us that all the corresponding angles will be congruent. 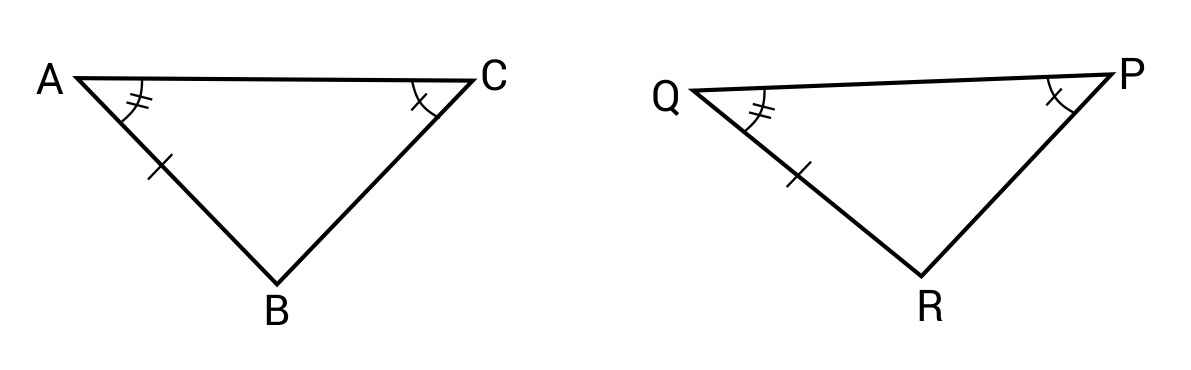
Congruent angles are commonly used in the study of geometry and in many real-world occupations. Construction workers, engineers, builders, and artists use congruent angles on a regular basis. Determining whether angles are congruent is an important skill that helps lay the foundation for the study of geometry.
Angles are everywhere around us. They are used by engineers, architects, and artists to invent creative solutions to specialized problems and to create beautiful fixtures and works of art. Many times, the angles present in shapes and intersecting lines have relationships with each other that we can use to determine their measure. One such relationship is congruence.
If we say that two angles are congruent, we mean that they have the same measure in degrees. For example, suppose we build a square room where all the corners are 90°. Its four corners would all have congruent angles because they are all the same measure.
Similarly, we know an isosceles triangle has two angles with the same measure. These two angles are therefore congruent. To denote that some angles are congruent to each other, we usually draw an arc in the angles.
Congruent angles really start popping up when we observe the intersections of straight lines. For example, if one straight line intersects another as shown, we can see that there are pairs of congruent angles created, opposite to each other. Because both lines are straight, the angles on each side are basically mirrored so that the red angles are congruent, and the blue angles are congruent. We call these angles vertical angles.
It is also helpful to note that because the lines are straight, two adjacent angles together form a straight angle of 180°. This property will come in handy when you need to solve for missing angles.
Let’s try an example. If angle \(A\) is 40°, what are the measures of angles \(B\), \(C\), and \(D\)?
Because the two intersecting lines are both straight, we know that the opposite angles \(A\) and \(C\) are congruent. Therefore \(C\) must be 40° as well. Similarly, angles \(B\) and \(D\) are congruent. Their measures can be determined using the fact that \(A+B\) must equal 180°.
\(40°+B=180°\)
\(B=140°\)
So \(B\) and \(D\) must both have measures of 140°.
What happens when we observe two parallel lines that are intersected by a third line?
Consider the parallel lines \(p\) and \(q\), and the transversal line \(t\) that cuts across them. We now observe two intersections and a total of eight angles.
A close look at these intersections reveals that they are identical to each other. Because \(p\) and \(q\) are parallel, their intersections with \(t\) form congruent angles. So, not only are angles 1 and 3 congruent, but angles 5 and 7 are also included in this same congruence. Likewise, angles 2, 4, 6, and 8 are all congruent.
There are four classifications for the types of congruent angles present in this scenario: vertical angles, corresponding angles, alternate exterior angles, and alternate interior angles.
Vertical angles are those which are opposite each other at a single intersection point. This is like we observed in the earlier example. Here, we see that angles 1 and 3 are again congruent, and because they are opposite each other at the same intersection, they are classified as vertical angles. Similarly, the pairs of angles 2 and 4, 5 and 7, and 6 and 8 are all vertical angle pairs.
Corresponding angles are pairs of angles in the same relative position of the intersection of each parallel line and transversal. Corresponding angles are congruent to each other. For example, angles 2 and 6 are corresponding angles because they both appear to the right of t and above the parallel lines. So, they are congruent angles. Other pairs of corresponding angles in this example are angles 1 and 5, 3 and 7, and 4 and 8.
Alternate exterior angles are pairs of angles that appear on the outsides of the parallel lines and on opposite sides of the transversal. Alternate exterior angles are congruent to each other. Angles 1 and 7 are alternate exterior angles and are therefore congruent to each other. Angles 2 and 8 are also alternate exterior angles, making them congruent to each other.
Similarly, alternate interior angles are pairs of angles which appear on the inside of the parallel lines and on opposite sides of the transversal. Alternate interior angles are congruent to each other. Here, that would be the pairs 3 and 5, and 4 and 6.
We’ve discussed that two or more angles are congruent if they share the same angle measure and we have looked at a few geometric applications of congruent angles. These ideas help builders, carpenters, and engineers ensure perfection in their work as they design tools, objects, and buildings. Take some time to work through some example problems on your own, and you’ll soon be seeing congruent angles in the world all around you!
I hope this video was helpful. Thanks for watching, and happy studying!
Congruent Angle Practice Questions
Angles 1 and 2 are corresponding angles. If the measure of Angle 2 is 67°, what is the measure of Angle 1?
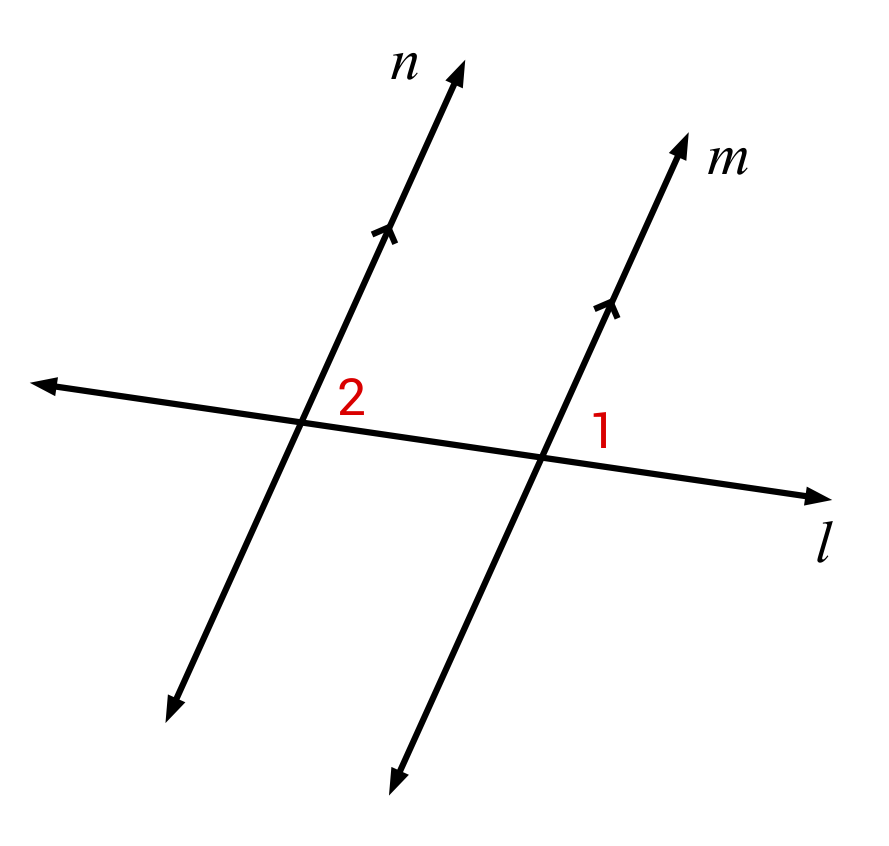
When two parallel lines are cut by a transversal, the angles that are on the same side of the transversal and in matching corners, will be congruent. Angles 1 and 2 are congruent angles, so both have an angle measure of 67°.
Line r is a transversal that crosses through the two parallel lines s and t. List all angles that are congruent to Angle 6.
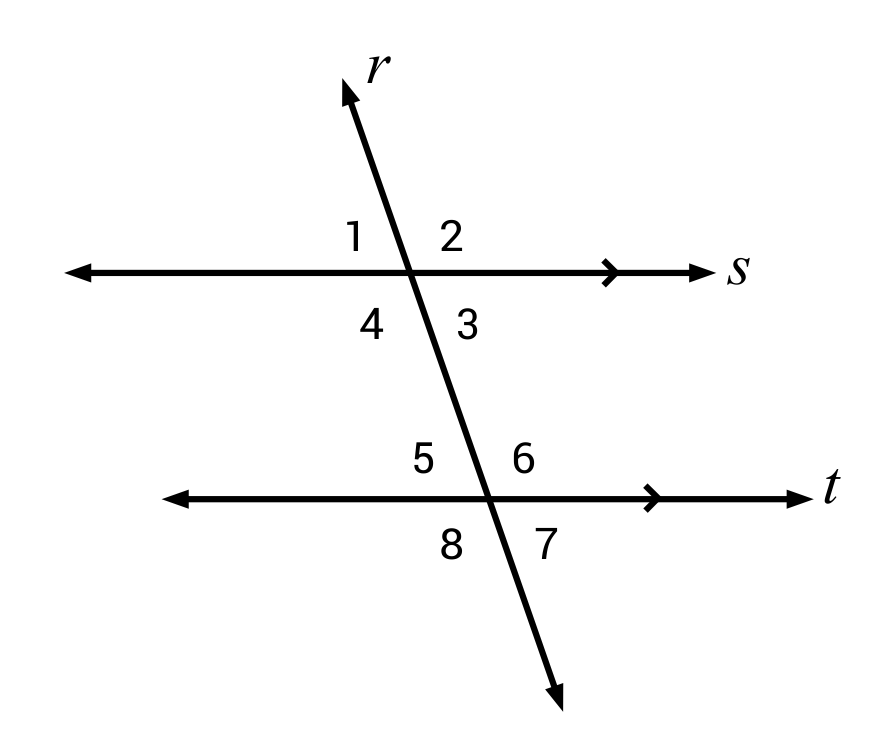
∠8 is congruent to ∠6 because they are vertical angles, or opposite angles.
∠2 is congruent to ∠6 because they are corresponding angles (same side of the transversal and in matching corners).
∠4 is congruent to ∠6 because they are alternate interior angles (alternate sides of the transversal, and between the two parallel lines).
If the following irregular quadrilaterals are congruent, Angle C must be congruent to what other angle?
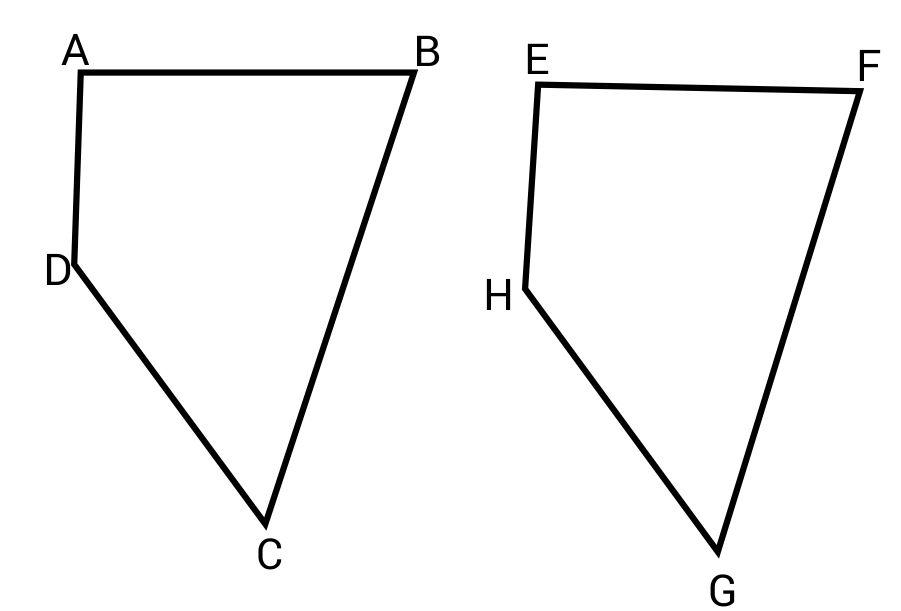
Corresponding angles are congruent for polygons that are congruent.
∠C is congruent to ∠G
∠D is congruent to ∠H
∠A is congruent to ∠E
∠B is congruent to ∠F
The city of Seattle is building a walking path that crosses over a pair of railroad tracks. The walking path is represented by the transversal t in the image below. The railroad tracks are represented by the parallel lines l and m. If the city wants to have the walking path cross the tracks at a 135° angle (Angle 1), what will the values of Angles 2, 3, and 4 be?
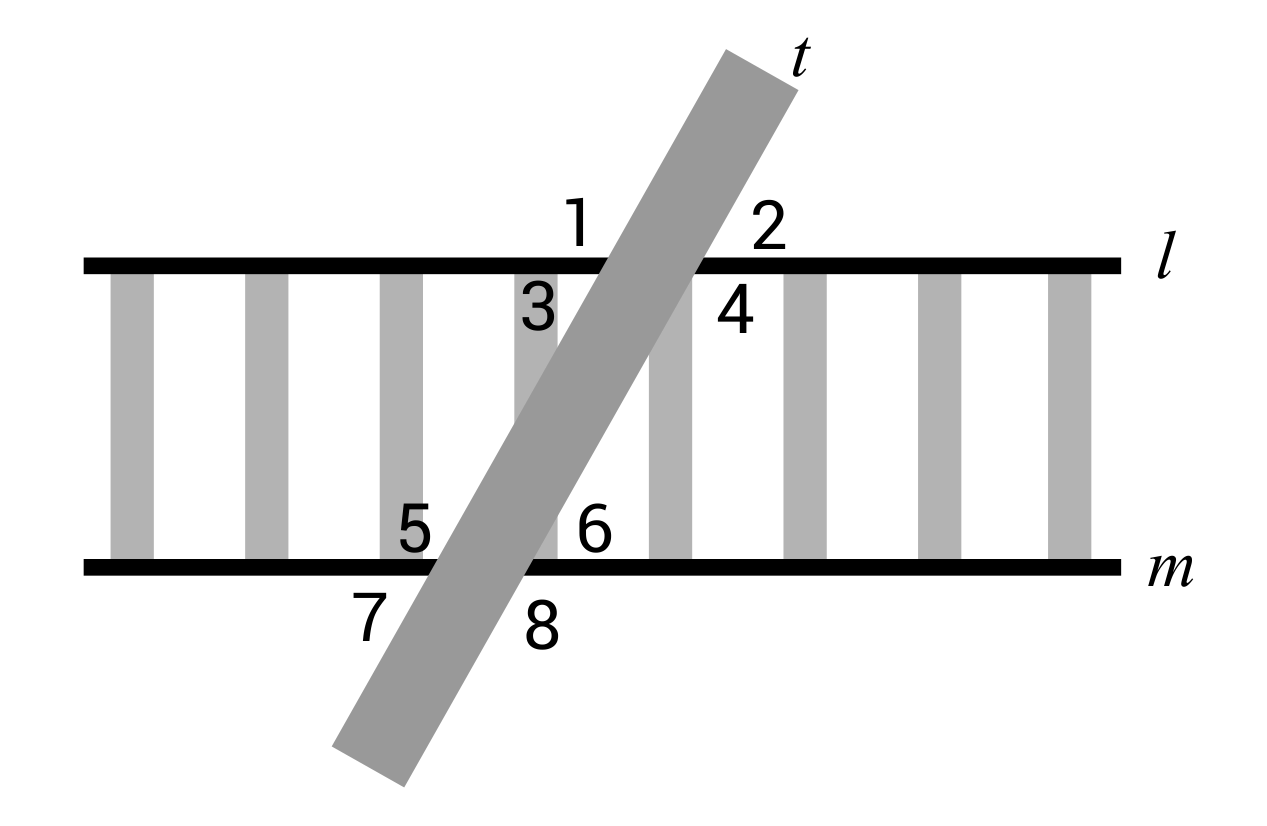
∠1 and ∠4 are congruent because they are vertical angles. If ∠1 equals 135°, then ∠2 must be equal to 45° because their sum needs to be 180° in order to form a straight line. Now that we know ∠2 equals 45°, we also know that ∠3 equals 45° because they are vertical angles.
Kelcy has a rectangular garden that she wants to divide equally into two sections diagonally. One section will be for carrots and the other section will be for kale. She separates the garden into two triangular pieces similar to the image below. If the measure of ∠DCA is 40° what is the measure of ∠CAB?
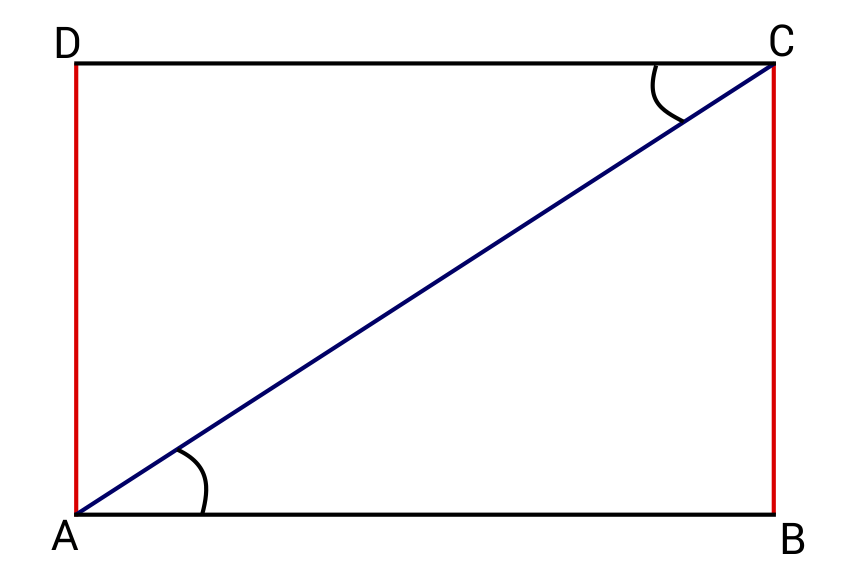
If the line AC forms a transversal through the parallel lines DC and AB, then the angles DCA and CAB will be congruent. Angle DCA and Angle CAB form alternate interior angles, so the measure of Angle CAB will be 40°.










