
Hi and welcome to this video about polygons! In this video, we will explore four things:
- What polygons are
- The different parts of a polygon
- Ways to classify polygons
- How to determine the number of diagonals in a polygon
The term polygon is derived from the Greek words polys meaning “many” and gonia meaning “angle”. So, polygons have many angles.
How Polygons are Constructed
First let’s explore how polygons are constructed.
Zero Dimensions
Consider the geometric point, represented by a dot:

The point is 0-dimensional—it has no length, width, height, nothing.
One Dimension
Now, let’s consider two connected points:

This is called a line, or a line segment. A line segment is 1-dimensional. It has length, but no width or height.
Two Dimensions
When multiple line segments are connected end-to-end, polygons such as this, can be formed:

Polygons are two-dimensional. They have no thickness, like this.
In order to be a polygon, the shape must be closed. In other words, every endpoint must be connected to another endpoint. This figure is comprised of connected segments, but the result is not a polygon.
This shape is closed, but not made up of connected segments, so it is also not a polygon:

Edges and Vertices
The sides of polygons are called edges and the angles created where the edges intersect are called vertices. Polygons also have as many edges as vertices:

Polygons are named by the number of edges they have. This polygon has three edges and three vertices and is called a triangle. The triangle has the smallest number of edges and vertices of any polygon—it is impossible to create a two-sided polygon.
Some common polygons are quadrilaterals (which have four sides), pentagons (which have five sides), hexagons (six sides), heptagons (seven sides), octagons (eight sides), nonagons (nine sides), decagons (ten sides) and dodecagons (which have twelve sides).
N-gon
Though polygons with any number of edges have names, the general \(n\)-gon is typically used for all other polygons, where \(n\) represents the number of sides. For instance, a 30-sided polygon is called a triacontagon, but it’s often simply called a 30-gon.
Regular vs. Irregular
Polygons can be regular or irregular. Regular polygons have congruent edges and congruent vertices. For example:
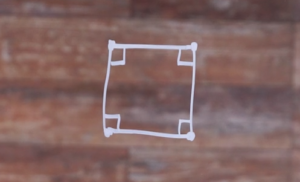
This is a regular quadrilateral. The edges are the same length and the vertices have the same measure.

This is an irregular quadrilateral. The vertices have the same measure, but the edges have different lengths.
This is an irregular quadrilateral. The edges are the same length, but the vertices have different measures.
This is an irregular quadrilateral. Neither the edges nor the vertices have the same measure.
Convex vs. Concave
Polygons can also be convex or concave. When one or more vertices of a polygon measures more than 180 degrees, the result is a concave polygon. For example:

This is a convex hexagon. All of the vertices measure less than 180 degrees.
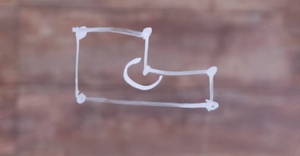
This is a concave hexagon. One vertex measures more than 180°.
Now remember:
- Only polygons with 4 or more sides can be concave because it’s not possible for a triangle to contain an angle measuring more than 180°, which is a straight line.
- Concave polygons cannot be regular because all the vertices will never be the same measure.
Polygons also contain diagonals. Diagonals are line segments joining two vertices that are not next to each other.
As you can see here, this irregular convex pentagon has five diagonals.

This is an irregular concave pentagon.

It also has five diagonals, even though the concavity causes diagonals to lie outside the polygon.

Triangles do not have diagonals because there is no way to connect two vertices with segments that are not edges.
Now that you know the basics of polygons, let’s use the diagrams to figure out a formula for finding the number of diagonals in any polygon.
Finding Diagonals
In this case, the number of diagonals connecting to each vertex is 2, which is 3 less than the number of vertices, 5: 2 diagonals connected to each vertex.
This is true of all diagonals of all polygons. A nonagon has \(9-3=6\) diagonals connecting to each vertex.

The number 3 is not arbitrary here – from any vertex, diagonals cannot connect to the vertex itself or to the vertices that they are “1 away” from, because it would be edges. That makes 3 vertices from every vertex that aren’t included. To generalize this, we’ll use \(n-3\), where n is the number of vertices of the polygon.
Now, each vertex has the same number of diagonals connecting to it, so in this case, we can see that the total number of diagonal connections to vertices is \(5(5-3)=10\).
In general, we can say the total number of diagonal connections is \(n(n-3)\).
When we figure out this total, though, we are counting each diagonal twice, because diagonals have 2 endpoints. In order to figure out the number of unique diagonals, we need to divide our total by 2. In our pentagon, this looks like:
Therefore, for any sized polygon, our equation can be written as this:
Conceptually, this can be remembered as:
Using our formula, we can determine the number of unique diagonals in, for example, a 17-gon:
We can also see algebraically that triangles have no diagonals:
We can also figure out how many edges or vertices a polygon has by the number of unique diagonals.
Suppose a polygon has 44 unique diagonals. How many edges does the polygon have?
\(n(n-3) = 88\)
\(n^2 – 3n = 88\)
\(n^2 – 3n – 88 = 0\)
\((n + 8)(n-11) = 0\)
\(n = -8\text{ or }n = 11\)
Alright, so here we are at our answer, \(n\) (the number of edges the polygon has) is either equal to 11 or -8. Because what we want to do is we want to make sure that we end with a result of 0, which means that \(n\), somewhere, has to be 11 or -8 in order to get us multiplying 0 by another answer, resulting in 0. Since \(n\) can’t be negative (cause we can’t have negative edges), it can’t be -8. So we know that our answer is 11. The number of edges is 11, making it an 11-gon.
Alright, excellent! I hope this video helped increase your knowledge of polygons and made some of their properties a little bit clearer! Thanks for watching, see you next time!
Polygon Practice Questions
Choose which of the following is a polygon:


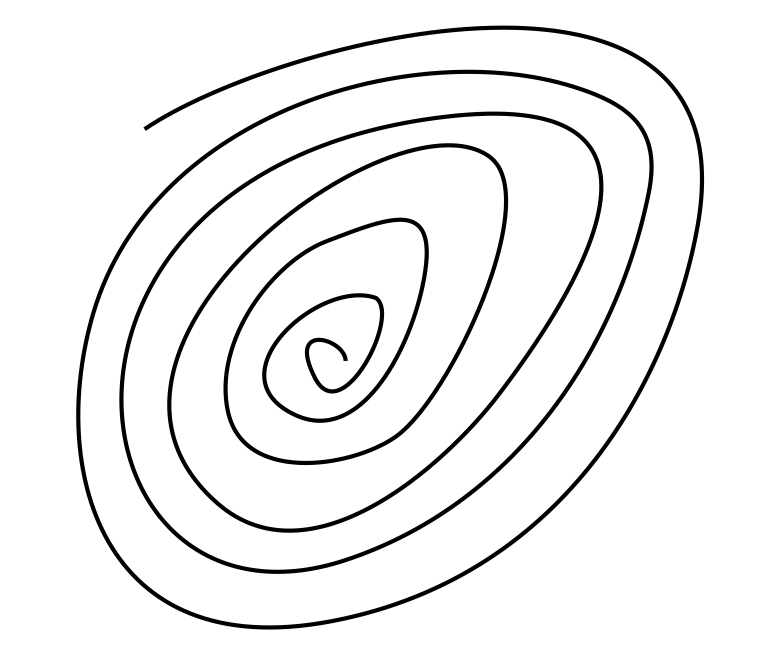
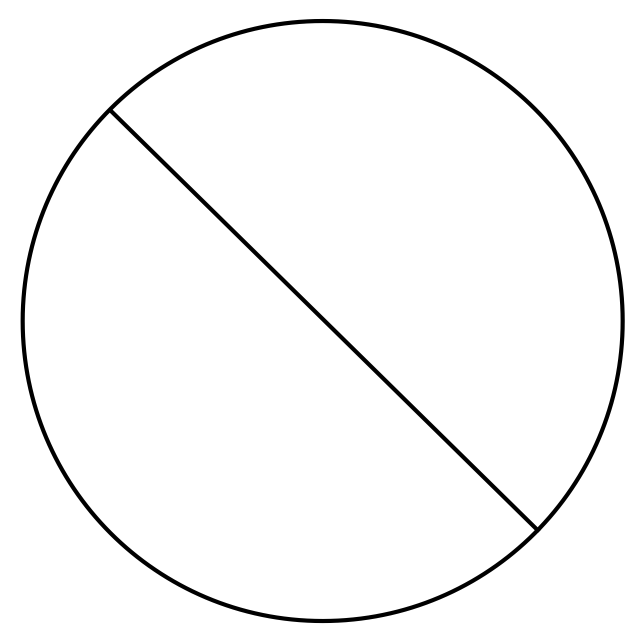
The correct answer is A. This shape is closed (every endpoint is connected to another endpoint), which is only possible when there are 3 or more “endpoints” or vertices– and there are just as many edges (sides) as there are vertices; making this a true polygon.
Let’s look into why answers B, C, and D are not polygons:
The circle is not a polygon because it is essentially just one continuous edge. There are no endpoints that we are connecting with individual line segments.
The spiral is not a polygon because it is not a closed shape. Additionally, there are only two endpoints/vertices.
Finally, the “No” symbol is clearly very similar to the circle. While it may be tempting to call it a polygon because there is a distinct edge connecting two vertices that runs through the middle of the shape, there are still only two vertices (and technically only one edge).
Which of the following is an irregular polygon?

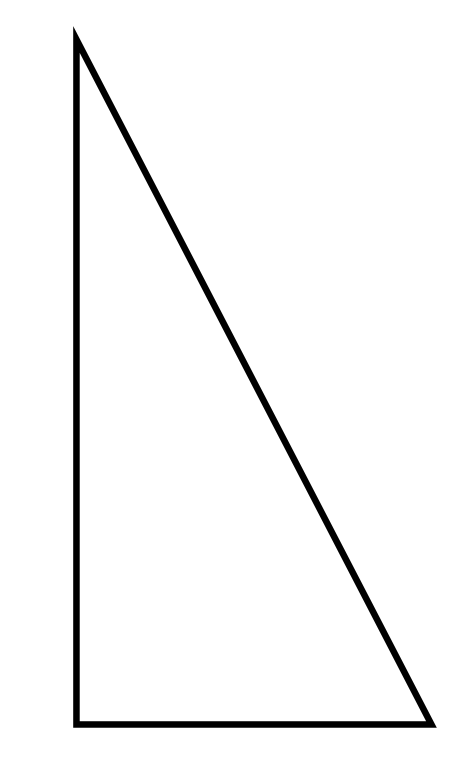

The correct answer is B. While the equilateral triangle (Shape A), the square (Shape C), and the regular hexagon (Shape D) each have edges that are each the same length and same-degree angles at each vertex, the right triangle shown in Choice B has edges and angles that measure different lengths/degrees.
Is this a concave or a convex polygon?
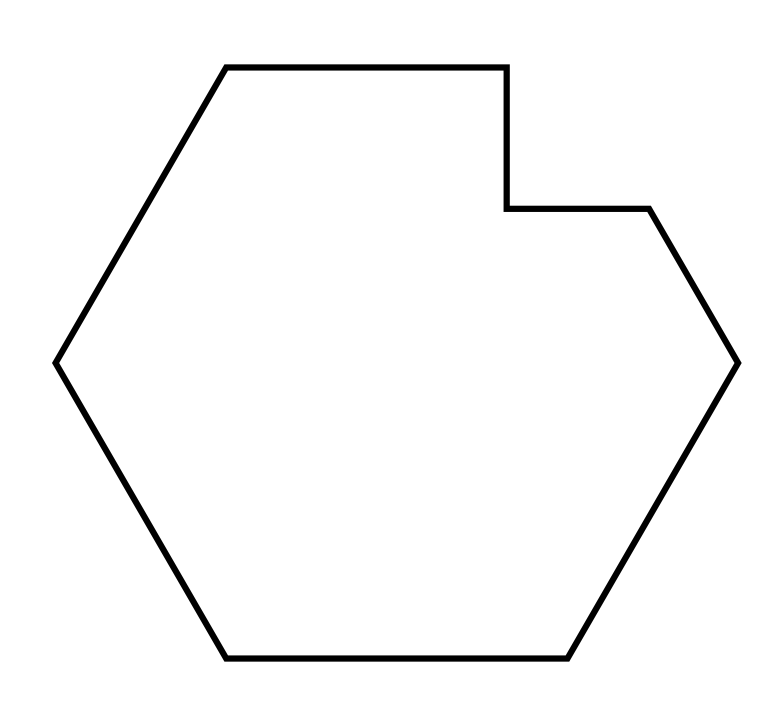
The correct answer is A. This is a concave polygon, and we can see this in the top, right-hand portion of the shape:
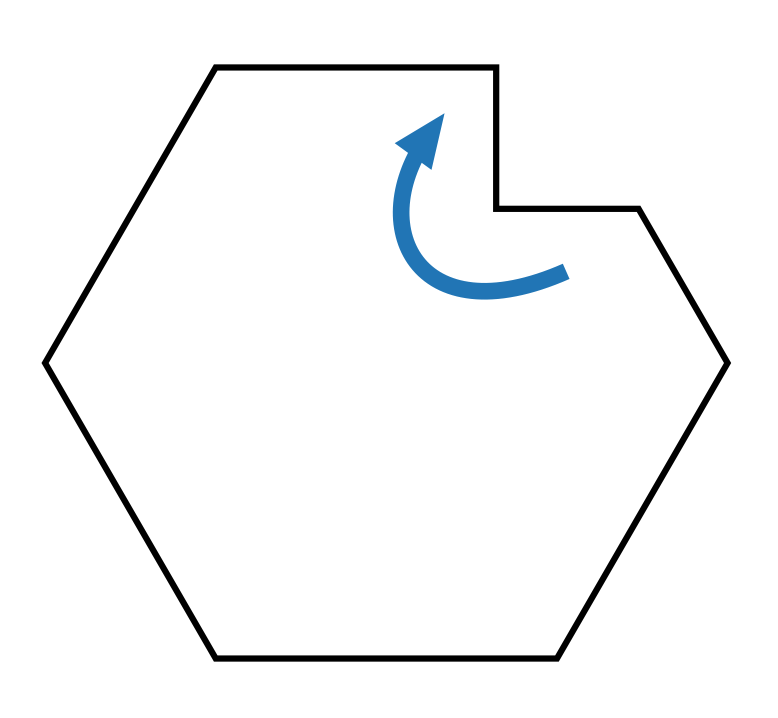
This angle sitting inside of the polygon is larger than 180°. There’s a portion of the shape “caving in on itself.”
How many unique diagonals does this polygon have?
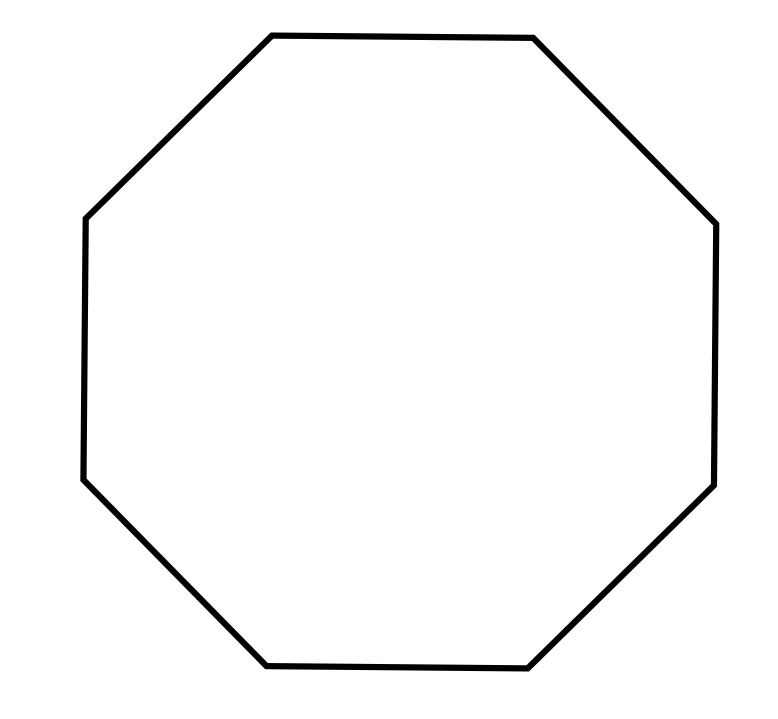
The correct answer is D. Since this shape is a relatively “simple” shape, we could feasibly count the diagonals by hand… but it would be far easier (and far more efficient) to use our given formula for determining the amount of unique diagonals in any polygon: \(\frac{n(n-3)}{2}\) (where n represents the amount of vertices [or edges] that that polygon has).
This octagon has 8 vertices, so we find that \(\frac{8(8-3)}{2}=20\).
Given that some n-gon has 77 unique diagonals, find the value of n.
The correct answer is C. This time, we must “work backwards” with our \(\frac{n(n-3)}{2}\) formula. We set our equation up like this:
\(\frac{n(n-3)}{2}=77\)
and our goal is to solve for n.
\(\frac{n(n-3)}{2}=77\)
\(n(n-3)=154\)
\(n^2-3n=154\)
\(n^2-3n-154=0\)
At this point, we’ll need to employ the quadratic formula to find the two possible solutions…
\(n=\frac{-(-3)\pm\sqrt{(-3)^2-4\times(1)\times(154)}}{2\times1}\)
\(n=\frac{3\pm\sqrt{9+(4\times154)}}{2}\)
\(n=\frac{3±\sqrt{9+616}}{2}\)
\(n=\frac{3±\sqrt{625}}{2}\)
\(n=\frac{3±25}{2}\)
\(n=14\) or \(n=-11\)
Out of these two possible solutions for n, only one of them makes sense for us! The value of n must be \(n=14\) because we cannot have a negative number of edges or vertices in a polygon.