
Hi, and welcome to this video on lines and planes!
The study of geometry is very much language-based, meaning that there are countless terms, relationships, and figures with meanings that are dependent on an understanding of other concepts. It can get pretty confusing if the foundational terms are not understood.
In this video, we’re going to start with the most basic figures: a point, a line, and a plane. These “undefined” terms are described, rather than being defined, and they support the definitions of all other geometric terms.
Points, Lines, and Planes
Points
To start off, what is a point?
A point is described as a very specific location, or position, in a plane. The notation for a point is a dot, but that dot does not have any dimension (length, width, circumference). A point is named with a capital letter, as in “point A”
Lines
A line is described as a “path,” as if a point was dragged or is moving. A straight line extends infinitely in opposite directions.
A line is typically named with a lowercase letter, or by referencing two points on the line, with a line symbol above. The line notation has arrows on either end to indicate that they extend forever. Points that lie on a line are referred to as collinear.
Planes
A plane surface has length and width, and extends infinitely in all directions. A flat surface, like a wall, floor, or ceiling, can be imagined as finite planes where geometric figures, like points and lines, can be drawn.
A plane is typically named with a letter in script or italics (plane m) or by naming three points that lie on the plane, (plane ABC). Using three points in the naming of a plane lends to the perception of a two-dimensional surface. Points that lie in the same plane are said to be coplanar.
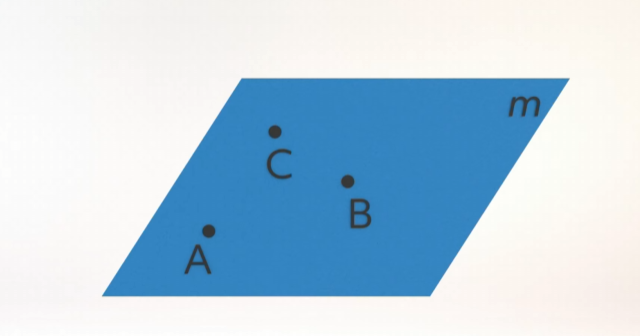
Planes that intersect do so at a line, and it is possible for three planes to intersect at exactly one point.

Other Important Terms
Now that we know these basic components, we can build our knowledge with terms that incorporate them in their definitions.
Line Segments
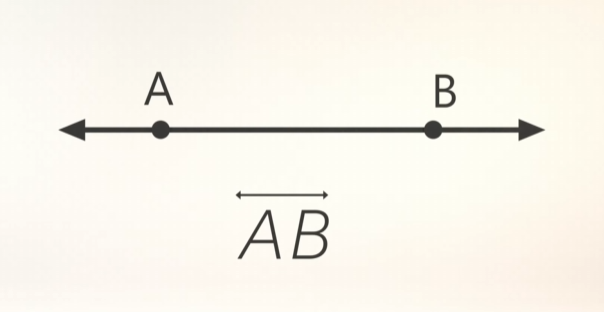
A line segment is the portion of a line that lies between two points on the line. The two points are called endpoints, and are included in the line segment, as are all the points that are between them. A line segment with endpoints A and B would be referenced as \(\overline{AB}\).
Rays
A ray starts at one point and extends infinitely in one direction on a plane. The ray symbol has one arrow indicating the starting point and the direction of the ray.
Intersecting Lines
When two lines on a plane cross each other, they are referred to as intersecting lines. Intersecting lines on a plane cross at exactly one point.
Because a line segment has length that can be measured between the endpoints, the exact midpoint of the segment can be determined. A point, line, or ray, or plane that crosses a line segment at the midpoint is called a bisector.
Perpendicular Lines
Intersecting lines on a plane that cross at 90° angles, or “right angles,” are perpendicular to each other.
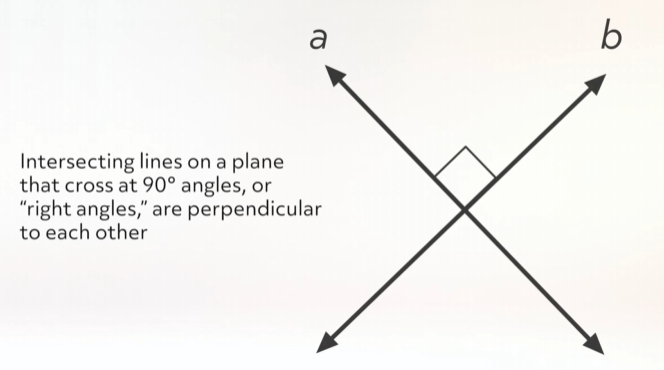
Examples of perpendicular lines can be found on window panes, or on door frames.
Parallel Lines
Lines on a plane that never cross are called parallel. These lines are exactly the same distance apart at all points, like the double yellow lines on a road, or tire tracks of a car.
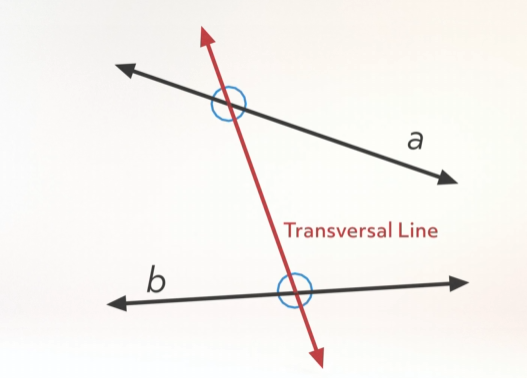
Transversal Lines
A line that crosses two lines in a plane at two distinct points is called a transversal line. Transversal lines in combination with special angle relationships are used to determine whether lines in a plane are parallel.
As you can see, it is essential to understand the relationships between the “undefined” terms of a point, a line and a plane in order to strengthen and expand your understanding of other geometry concepts. It’s important to review these frequently from the ground up to keep pace and to retain your knowledge.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What are lines?
A
In the context of mathematics, a line is an infinitely long collection of points. A line has no width or depth*, and it will continue to run in opposite directions forever. We designate that something is a line by marking arrows on both (visible) ends of a line segment.
*Because a line only has length as a dimension, it is a 1-dimensional object.
This: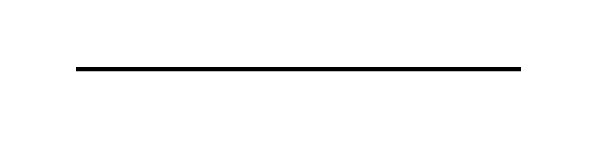
would not necessarily be considered a line in a math course because we don’t know if this object has specific endpoints or if it runs on forever.
However, we can turn this into a line by strategically placing 2 arrows: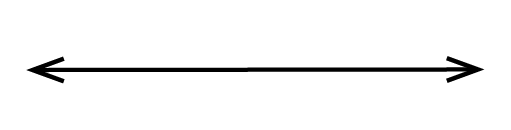
As you might guess, a line never has a visible ‘ending.’ In fact, a line doesn’t have any ending because it is infinitely long!
Q
How do you define a point?
A
A point is a set position (or “coordinate”) within a space. Traditionally, a point is designated by a simple ‘dot’ on some surface; and it’s either named by a single letter and/or described in \((x,y)\)– or \((x,y,z)\)-coordinate form.
Remember that a point is a dimensionless object because it doesn’t have any width, length, or depth.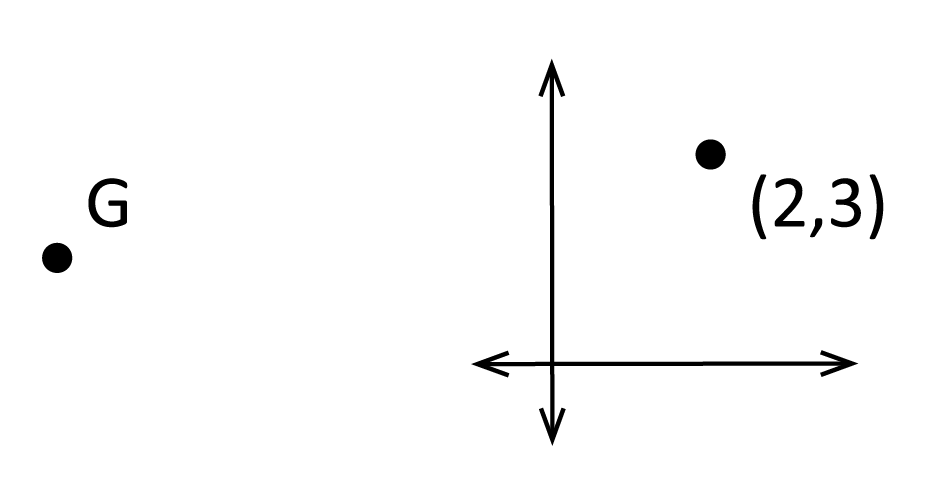
Q
What is a collinear point?
A
Collinear points are points that sit on the same line, line segment, or ray.
The points A, B, and C are collinear.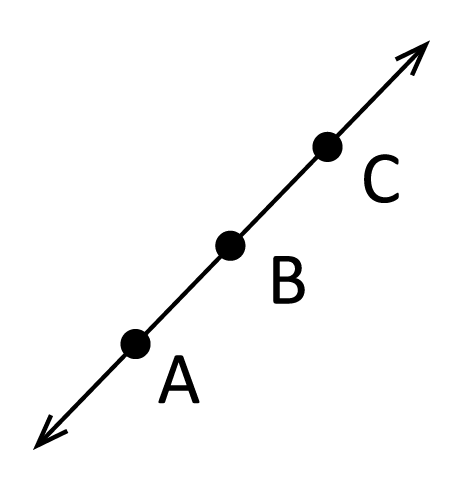
The points X and Y are not collinear because Y isn’t on the same line as X.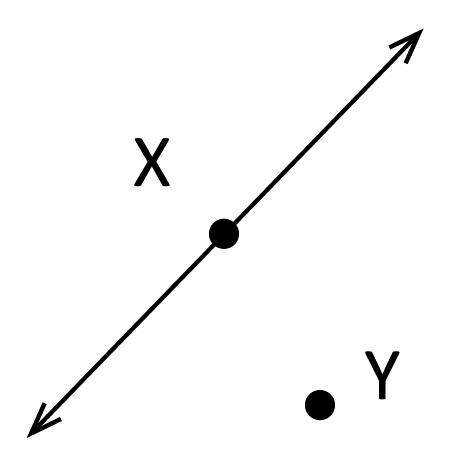
Q
What is a plane in math?
A
Think of a plane as the surface of an ever-lasting piece of paper: a flat surface that you can only move up and down or right and left on. You couldn’t move “in” or “out.” 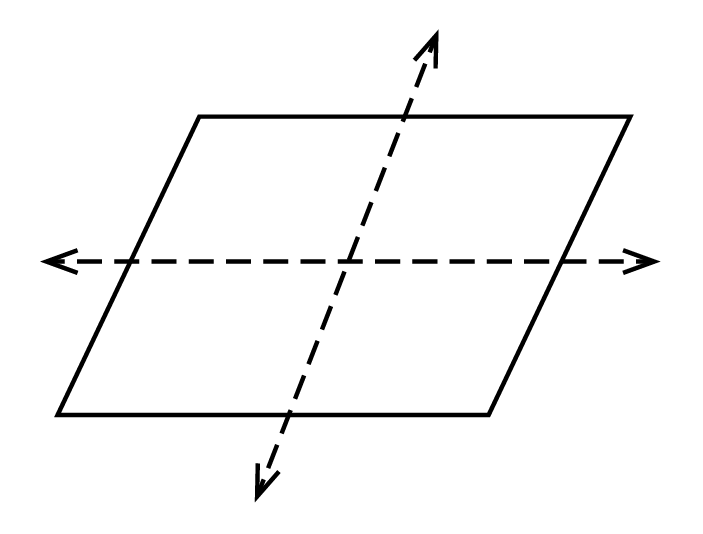
A plane is the collection of an infinite amount of points and lines, and it has both length and width (but no depth). Hence, a plane has only 2 dimensions.
We usually call it ‘the \(xy\)-plane,’ because we describe points and lines in relation to the horizontal axis, \(x\), and the vertical axis, \(y\).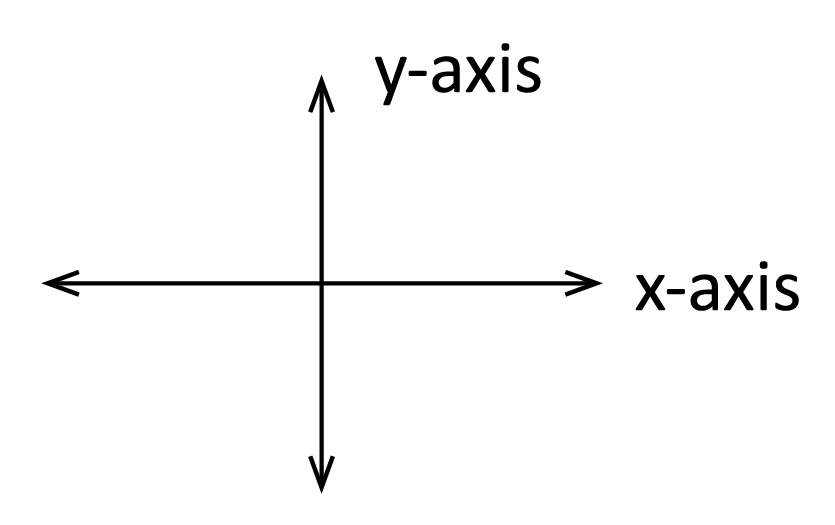
Q
How do you identify a plane?
A
There are a few different ways to identify/construct a plane:
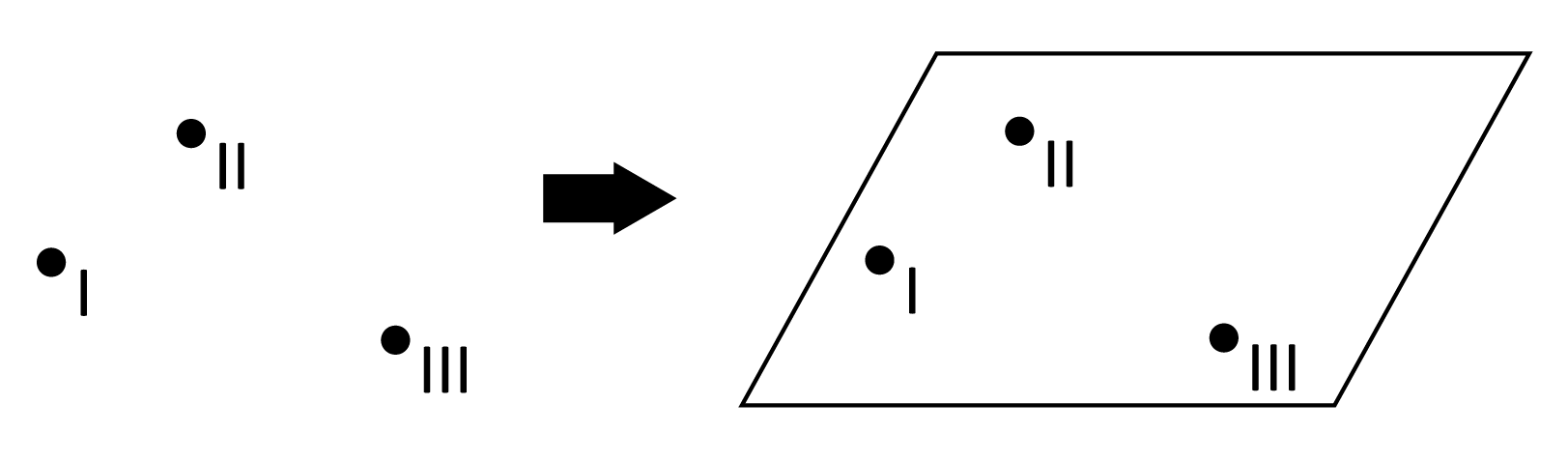
- Using 3 non-collinear points: When looking at a collection of 3 points that don’t sit on a line together, one might notice that the only way to “connect” the points to one another is to have them sitting on the same plane together.
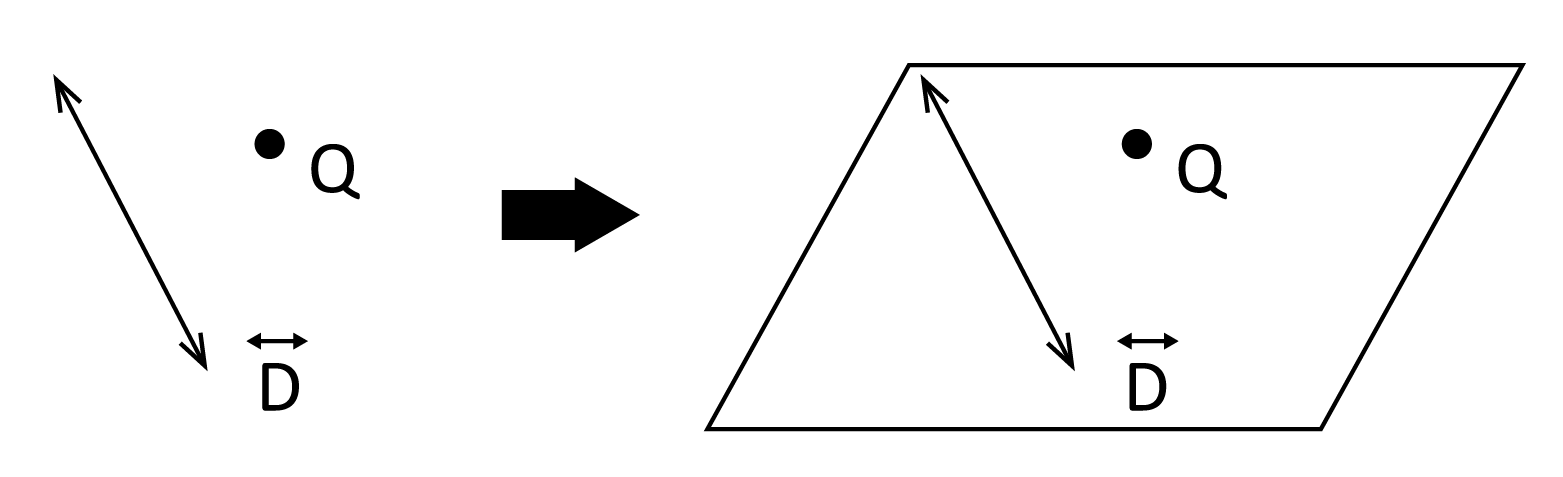
- Using a line and a separate point: This method is very similar to the one outlined above. Imagine that we drew a line connecting 2 out of the 3 points from above; the only way to connect the two new objects would, again, be to draw a plane.
- Using a pair of intersecting lines: Imagine that you have two lines that cross over one another at some shared point. There is only one way to sit these lines on the same flat surface, and so we construct a plane that gives the two lines ‘common ground.’
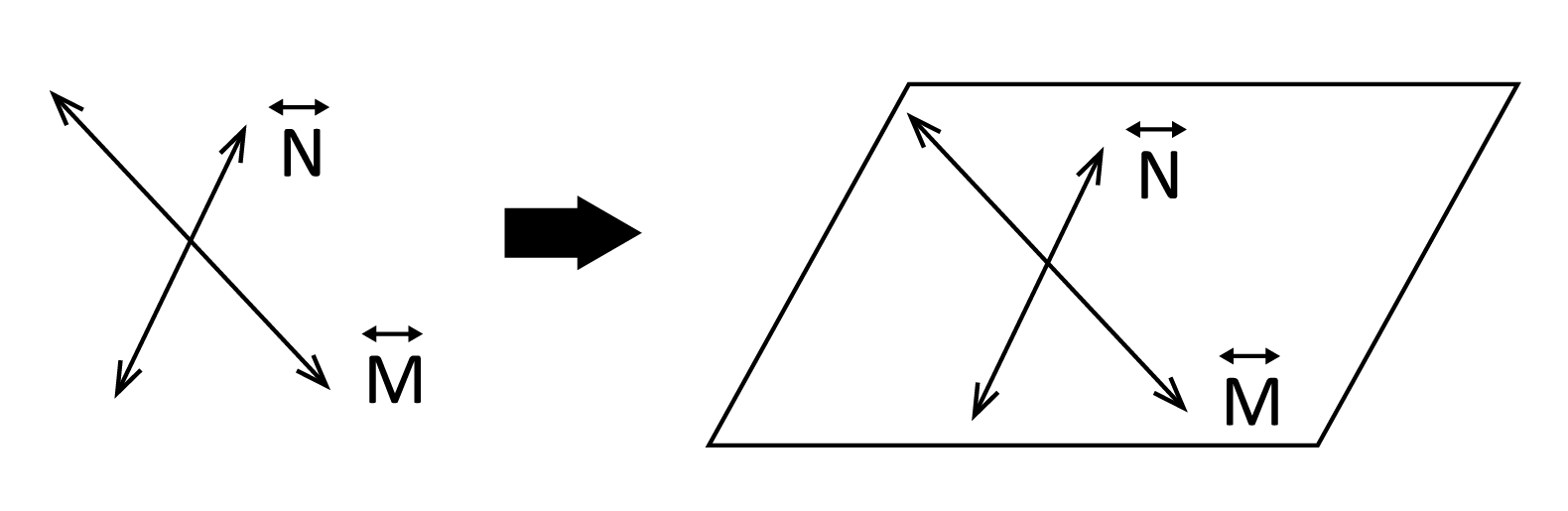
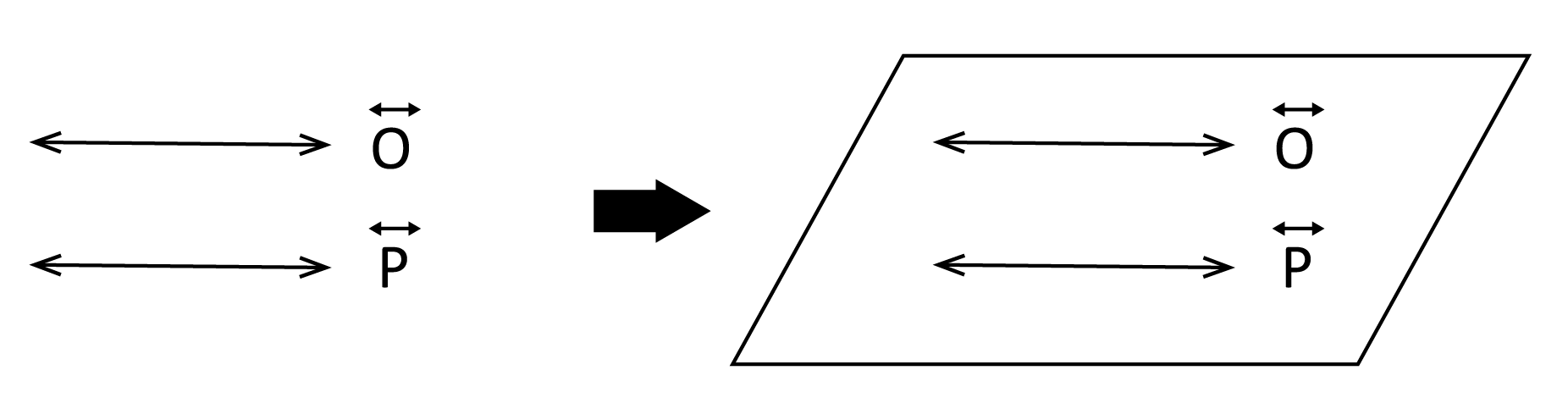
- Using a pair of parallel lines: Once again, this is similar to the intersecting lines method we just discussed. There is only one way to set up a plane for these parallel lines to sit on together.
Q
Does a plane always have 3 points?
A
Technically, yes- a plane always has at least 3 points; because a plane is a collection of infinitely-many points. However, we can’t identify or construct a plane given less than 3 points.
Let’s say that we’ve been given the point A, , and are told to, “find the unique plane that this point sits on.” Unfortunately, this is an impossible task! The amount of possible planes that we could come up with is endless.
, and are told to, “find the unique plane that this point sits on.” Unfortunately, this is an impossible task! The amount of possible planes that we could come up with is endless.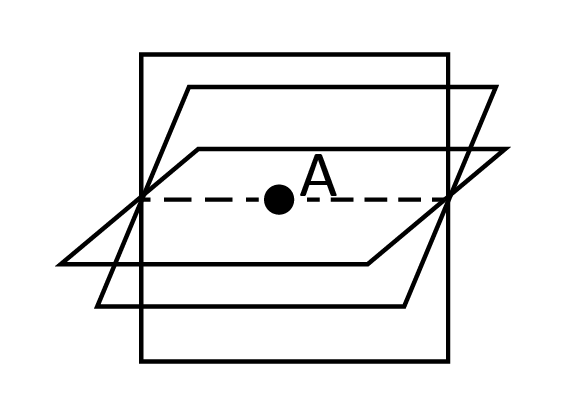
Now let’s say that we’ve been given the points E and F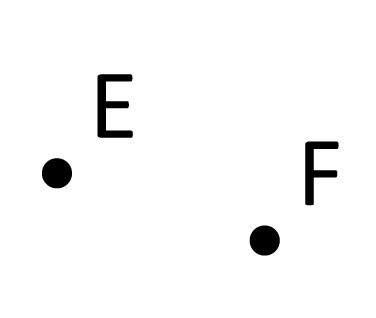
and told to find the plane (like above). While there’s only 1 unique line that connects this pair, again: we run into the problem that there are infinitely-many possible planes that the two points could be sitting on together.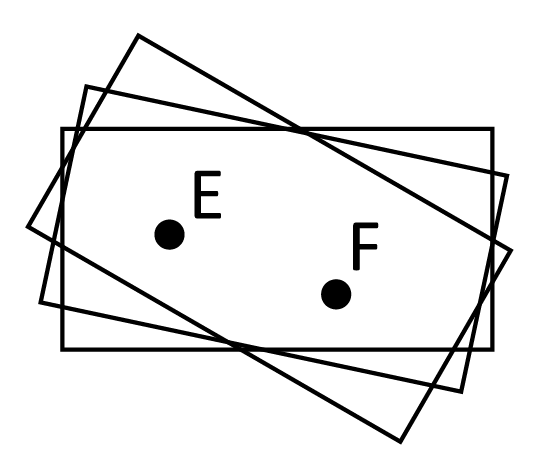
When you are given 3 points, you have made certain that the space you are looking at is a plane because there is only one unique plane that all 3 points can lie on
Q
Does one line define a plane?
A
No, a single line cannot be used to define a unique plane. As mentioned above, 1 line can sit on a countless amount of possible planes.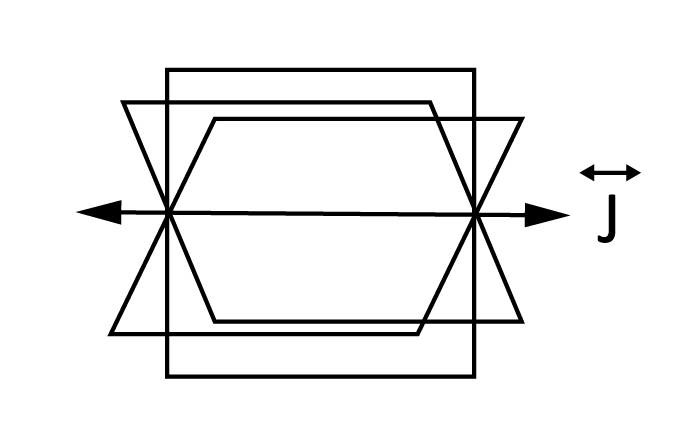
Q
What are line segments?
A
It might seem silly at first, but a line segment is actually quite different from a line in math. This distinction is important: while a line continues infinitely in both directions, a line segment has a finite length. More specifically, line segments run from one “endpoint” to another, and these endpoints are the points that sit on both ends of the line segment.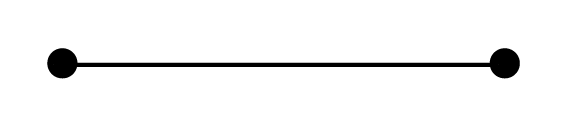
Q
What does a ray look like in math?
A
A ray is kind of like the combination of a line and a line segment; it has 1 endpoint, but on the opposite end it continues on forever.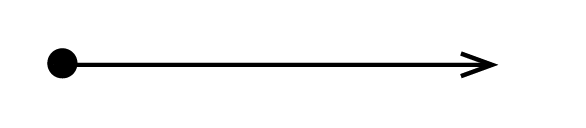
Q
What is the difference between intersecting lines and perpendicular lines?
A
While 2 lines are considered intersecting lines if they cross over one another at a particular point, they are only considered perpendicular to one another if all 4 angles formed at the intersection point are right angles (each measures 90°).
Keep in mind: all perpendicular lines are intersecting lines, but not all intersecting lines are perpendicular.
The lines A and B are simply intersecting. However, the lines C and D are perpendicular.
Q
What are parallel and intersecting lines?
A
There are only 2 possible relationships that a pair of lines can have between themselves: they are either parallel or they are intersecting (or will eventually intersect) one another.
If it’s impossible for 2 lines to ever cross over one another, they are considered parallel. If the lines cross over one another at some point (we call this point the “intersection point”), we call them “intersecting lines.”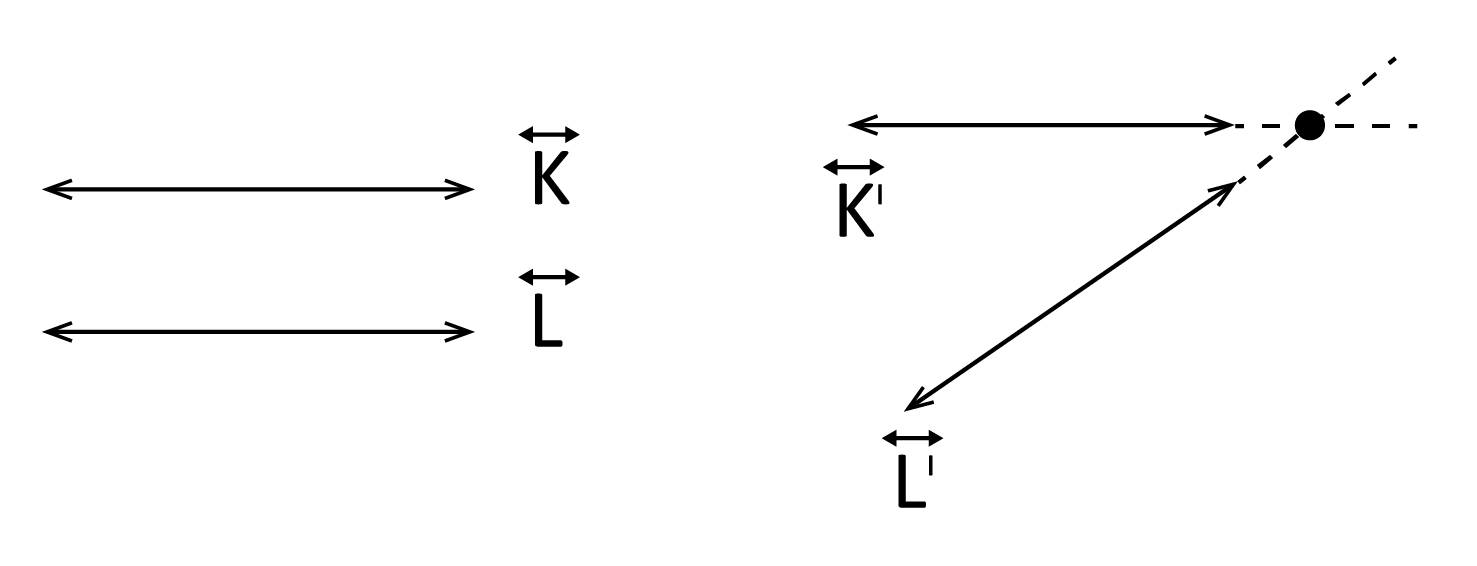
The lines K and L are parallel to one another; and while K’ and L’ are not yet intersecting, they will eventually meet at the intersection point to the right.
Q
How do you identify a transversal line?
A
A transversal line is one which intersects at least 2 other lines. In the following figures, the dashed line is the transversal: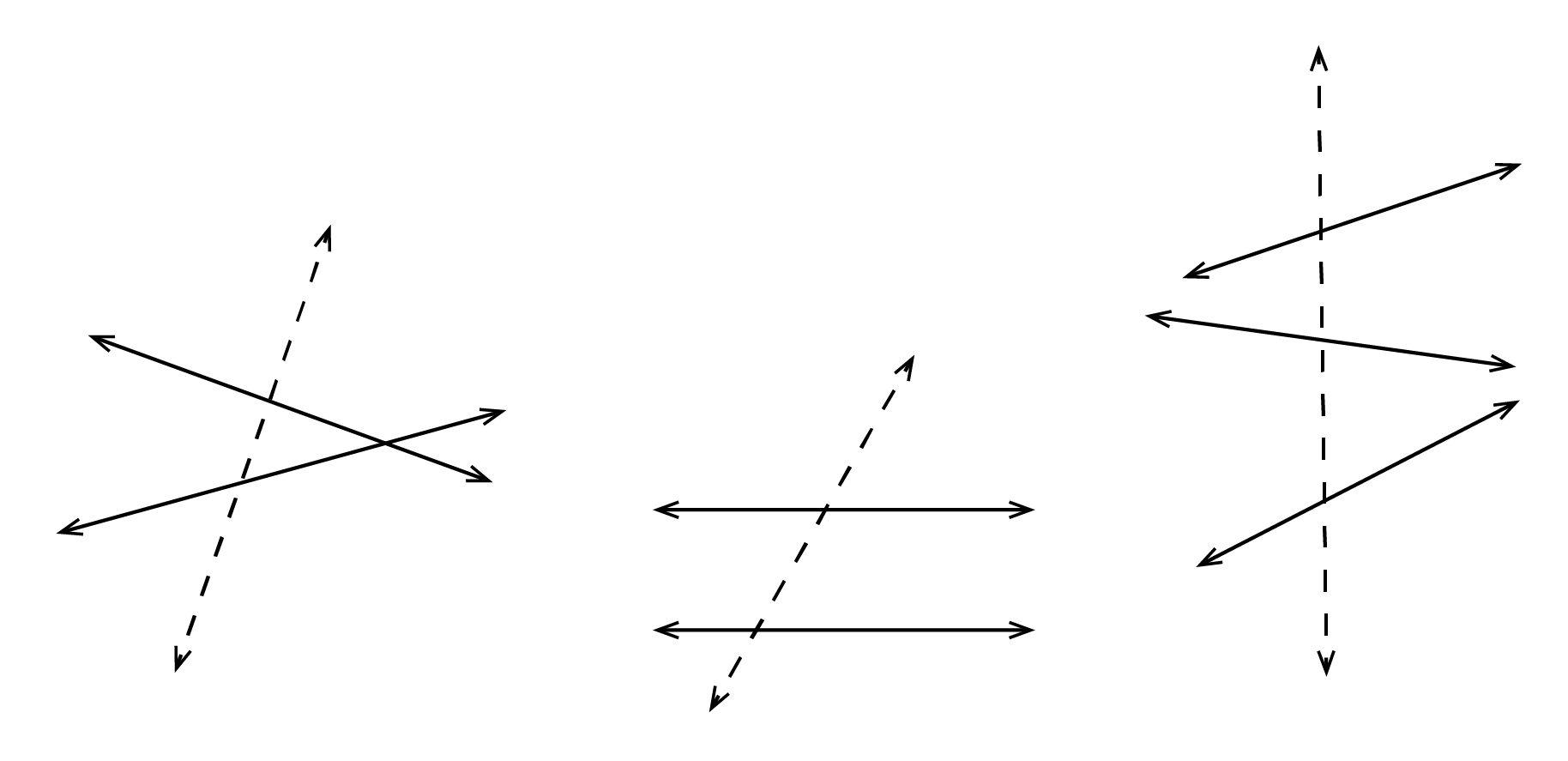
Lines and Planes Practice Questions
A ________ is a part of a line that has one fixed starting point, and extends infinitely in one direction.
A ray is a part of a line that has one fixed starting point, and extends infinitely in one direction.
Name the plane in the image below.
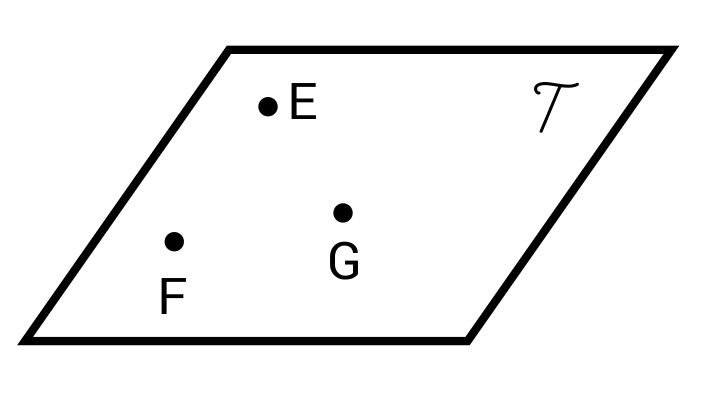
A plane can be named by an italicized letter such as T, or by three non-collinear points that lie on the plane, such as EFG.
Which capital letters in the alphabet have parallel lines.
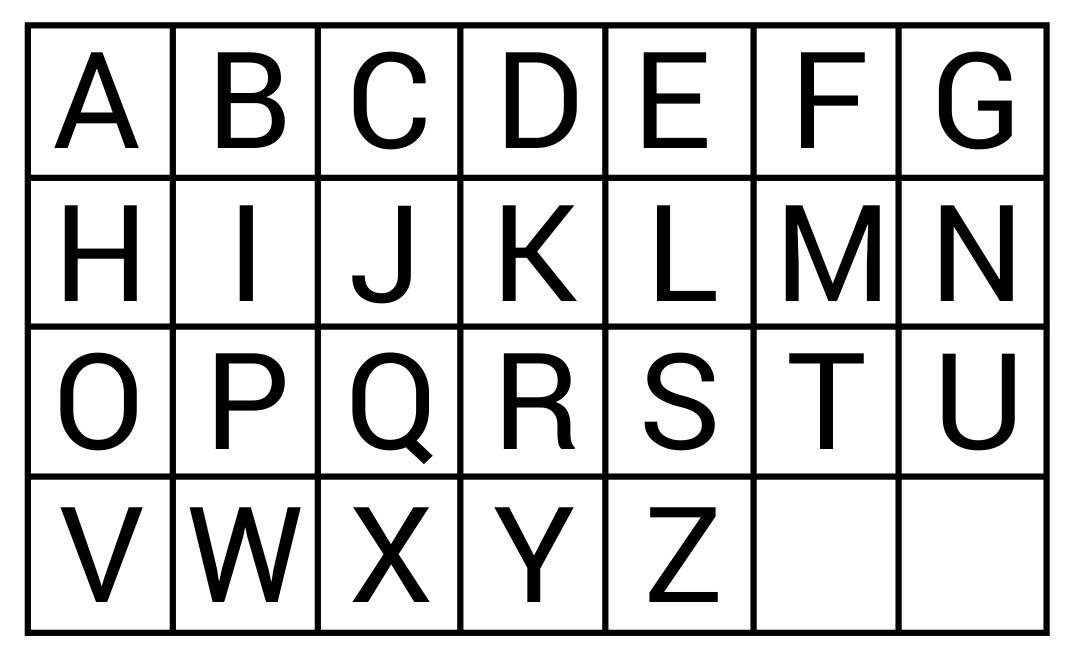
Parallel lines will never cross each other even when extended infinitely. The letters E, F, H, M, N, W, and Z consist of parallel lines.
Which geometric term best describes how the city of Austin, Texas would be represented on a globe?
A point describes a location, such as Austin, Texas on a globe. In geometry, a point does not take up space, but in pictures or diagrams they are drawn as dots.
Andrew wants to build a model of a skyscraper using paper. He decides to design the building as a triangular prism. How many planes will be used to create this model?


The model will be built from five planes: top, bottom, and three sides.