
Hi, and welcome to this video about the volume and surface area of a cube!
We see this shape everywhere, most commonly with blocks and dice. And then there’s the colorful puzzle known as a Rubik’s Cube, which is a cube that appears to be made up of smaller cubes.
In math, a cube is a special kind of rectangular prism. In most rectangular prisms, the length, width, and height of the shape can all be different. But in a cube, they’re all the same. That is to say that the edges are all the same length.
Volume of a Cube
There are two important measures of a cube. The first one is the volume. The volume of a cube or any other 3D object is a measure of how much space it takes up. We measure this in cubic units such as cubic inches or cubic centimeters. It’s easy to picture this with a cube. Just imagine that we have a bunch of little cubes that are one centimeter tall, one centimeter wide, and one centimeter long. Each one of these cubes is one cubic centimeter. This is our unit of measure.
Now let’s build something from these little cubes. Let’s build something that looks a lot like a Rubik’s Cube. We’ll start with the top level. We need to make a three-by-three grid of the cubes. Each cube is one centimeter tall and one centimeter wide. Once we’re done with that layer we can see that we’ve used nine cubes. Next, we build the middle level using another nine cubes. All together, 9 and 9 make 18 cubic centimeters. Finally, we build the bottom level, again using nine more cubes. All together we’ve got 27 cubic centimeters.
Our finished shape is a cube made up of smaller cubes. How many did we use? Nine on each layer for a total of 27. We used 27 one-centimeter cubes (or cubic centimeters) to make our bigger cube.
Volume of a Cube Formula
Fortunately, to find the volume of every cube we don’t need to build one out of smaller cubes—there is a formula we can use instead. The formula for the volume of a cube is \(V = a^3\). \(V\) is the volume and \(a\) is the length of an edge (remember that all the edges have the same length).
If we measure the area of this cube, we find that all the edges are 3 centimeters long. So to find the volume we can substitute 3 for \(a\) in our formula. We raise it to the third power \((3\times 3\times 3)\) which gets us \(27\text{ cm}^3\), which makes sense since we needed to use 27 of the little cubes to build our cube. Remember that it’s very important to specify the units when giving our answer.
Surface Area of a Cube
The other main measure of a cube is surface area. It’s an area measurement, so it’s in two dimensions. Imagine we were making a paper case for the cube we built earlier. How much paper would we need, in square centimeters? If we look at the cube we built earlier and just look at one side of it, we can see a bunch of these one-centimeter squares. If we count them we can see there are nine, in fact. So one side is made of nine square centimeters.
But to find the surface area of the cube we need the area of all the sides, not just one. Fortunately, since a cube is the same length, width and height that means that all the sides have the same area. And there are six sides. So we can multiply 6 sides by the area of one side (in this case, \(9\text{ cm}^2\)) to find a total surface area of \(54\text{ cm}^2\). That’s how much paper we’d need to make our paper case.
Surface Area of a Cube Formula
You may have seen a “map” like this:
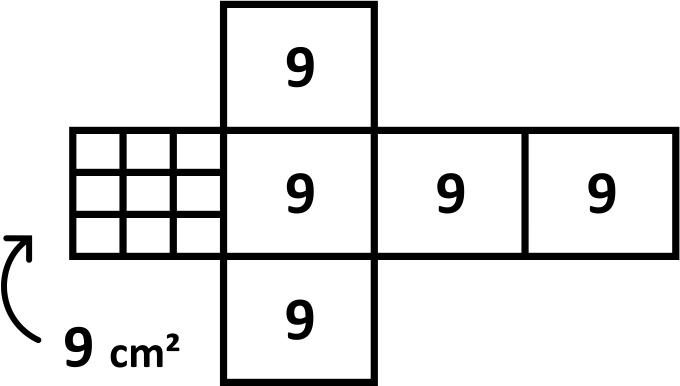
Just like with volume, we have a formula so we don’t have to build a cube each time we need to find the surface area. The formula is \(\text{Surface Area} = 6a^2\). The 6 represents the number of sides of the cube, and the \(a^2\) is the area for each side. We can confirm that this works by plugging in our edge length, \(6(3)^2\), and then evaluating the expression.
We need to remember to use the order of operations and apply the exponent before we multiply. If we do so, we see that we correctly figure out the surface area of \(54\text{ cm}^2\) for our cube.
Thanks for watching and happy studying!
Volume and Surface Area of a Cube Practice Questions
What is the surface area of this cube?
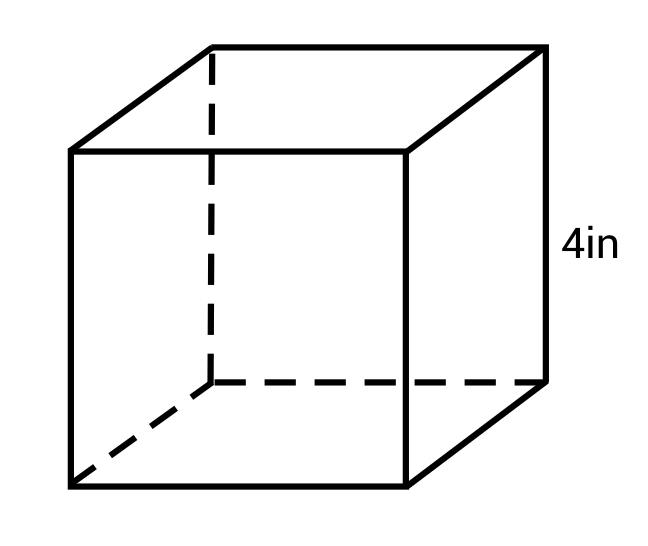
The correct answer is C: \(96\text{ in}^2\). The formula for surface area of a cube is: SA=6s2. Plug in 4 in for s and solve.
\(SA=6s^2=6(4)^2=6(16)=96\text{ in}^2\)
The surface area of the cube is \(96\text{ in}^2\).
What is the volume of this cube?
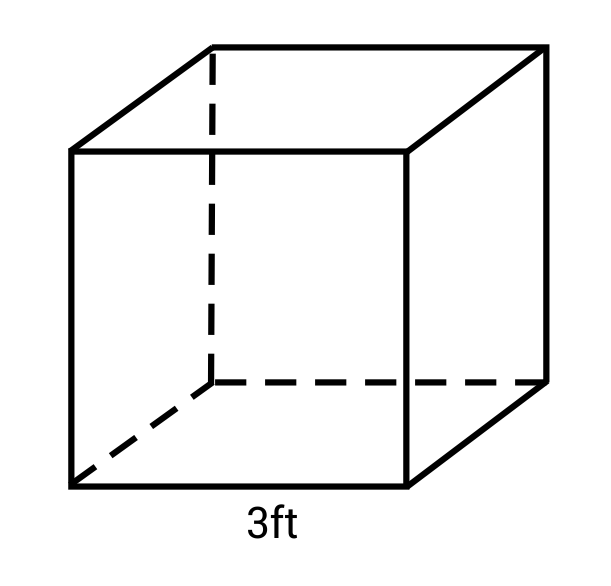
The correct answer is A: \(27\text{ ft}^3\). The formula for volume of a cube is: \(V=s^3\). Plug in 3 ft for s and solve.
\(V=s^3=(3\text{ ft})^3=27\text{ ft}^3\)
The volume of the cube is \(27\text{ ft}^3\).
What is the surface area of a cube with side length of 12 meters?
The correct answer is D: \(864\text{ m}^2\). The formula for surface area of a cube is: \(SA=6s^2\). Plug in 12 m for s and solve.
\(SA=6s^2=6(12\text{ m})^2=6(144\text{ m}^2)=864\text{ m}^2\)
The surface area of the cube is \(864\text{ m}^2\).
What is the volume of a cube with a surface area of \(96\text{ m}^2\)?
The correct answer is B: \(64\text{ m}^3\). To find the volume of a cube given the surface area, first use the surface area formula to find the side length, then use the side length to find the volume.
\(6s^2=96\text{ m}^2\)
\(s^2=16\text{ m}^2\)
\(s=4\text{ m}\)
The side length of this cube is 4 m. Now, plug this value into the volume formula and solve.
\(V=s^3=(4\text{ m})^3=64\text{ m}^3\)
The volume of this cube is \(64\text{ m}^3\).
If units are ignored, what is the difference between the volume and surface area of a cube with side length 7?
The correct answer is A: 49. To solve this problem, we need to plug 7 in for s and solve for both volume and surface area, and then subtract the two values. First, find the volume of the cube.
\(V=s^3=(7)^3=343\)
Then, find the surface area of the cube.
\(SA=6s^2=6(7)^2=6(49)=294\)
Finally, subtract the surface area from the volume.
\(343-294=49\)