How to Calculate the Volume of 3D Objects
Hey, guys! Welcome to this video on the volume of three-dimensional objects.
Let’s start off by defining volume. Volume is the measurement of how much space a liquid or gas takes up, or how much space a liquid or gas takes up within a given object.
You may not know it, but people use volume every day. Volume is used to calculate the drinking amounts. The amount of water you can hold in a cup is dependent on the volume of the cup. There are several other ways that volume is used.
Now, let’s look at how to calculate the volume of a triangular prism, a rectangular prism, a sphere, and a cone.
The Volume of a Triangular Prism
The area of a triangle is \(A=\frac{1}{2}bh\). Essentially, to find to the volume of the triangular prism, you are multiplying the area of the triangle times the length or depth. So, the formula for the volume of a triangular prism would be \(V=\frac{1}{2}bhl\).
Let’s take a look:
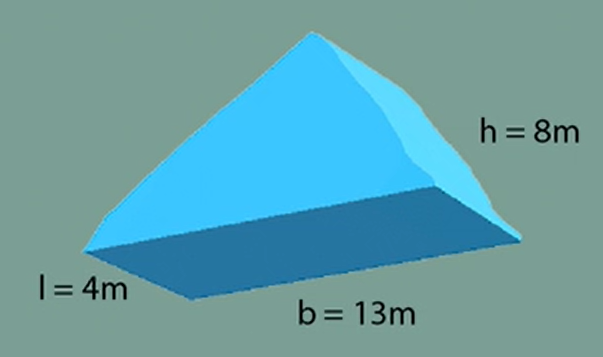
We have a triangular prism with a height of 8 meters, a base of 13 meters, and a length of 4 meters. All we have to do is plug our numbers into our formula then solve. So we have \(V=\frac{1}{2}bhl\). And once we solve, we get our answer, which is \(208m^{3}\). It’s important to know that, when dealing with volume, we will always have cubic units because we are multiplying the units by themselves 3 times.
Volume of a Cube or Rectangular Prism
To find the same volume of a cube or rectangular prism, you will use the same formula. Just like with the triangular prism, you want to find the area of one side, then multiply it times the length. However, it’s important to know that the formula you use to find the area of a triangle is not the same formula you use to find the area of a square or a rectangle. The formula for the area of both a square and a rectangle is \(A=b h\). So, to find the volume of a cube or rectangular prism, you would find the area of the square or rectangle then multiply it times the length. Which, makes the formula \(V=bhl\).
Here is an example:
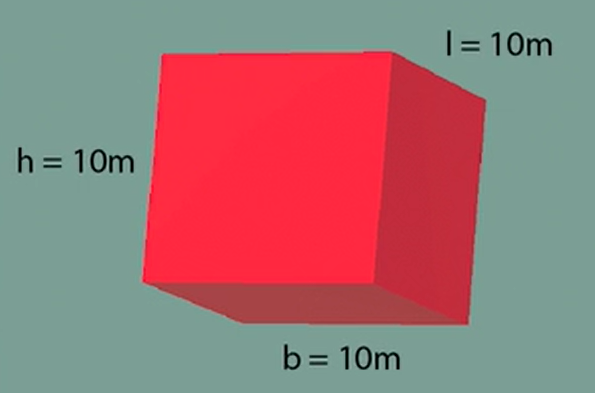
Here we have a cube, which is a rectangular prism, but all the sides are perfect squares. Because it’s a cube, we know that all of the sides are the same distance. So all we need to do is multiply 10 times itself 3 times. This gives us 1,000 meters cubed. Let’s try another:
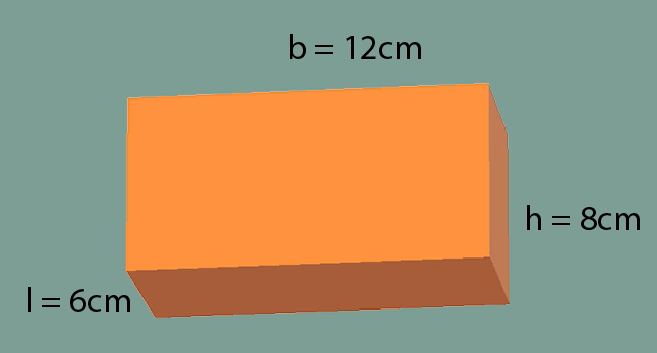
Here, we have a rectangular prism with sides that are different in distance. We have a base of 12 cm, a height of 8 cm, and a length of 6 cm. Now, all we need to do is plug those numbers into our formula, and once we solve, we get 576 cm cubed.
Volume of a Sphere
Now if you remember the area of a circle is \(A=\pi r^{2}\). That is pi times the radius squared. Well, to find the volume of a sphere you will use a similar formula, but multiply it times \(\frac{4}{3}\) and switching the \(r^{2}\) to make it \(r^{3}\). Making the formula for the volume of a sphere \(V=\frac{4}{3} \pi r^{3}\). When you do what is called a proof, to prove that this is the formula, but for now we’ll just plug the numbers into the given formula.
The sphere has a diameter of 20 meters. This is all the information we need to plug in and solve our equation. We are looking for the radius, and we know that the radius is equal to half of the diameter, which means that our radius is equal to 10 meters. When we plug 10 into our formula, and solve, we get 4,188.9 meters cubed.
Volume of a Cone
The formula for volume of a cone is very similar to the formula for the area of a circle. However, there are two things added to the formula. To find the volume of a cone, you multiply times \(\frac{1}{3}\), and times the height because now you have a height (because now you are working with a three-dimensional shape). This makes the formula for the volume of a cone \(V=\frac{1}{3}h\pi r^{2}\). Here is an example:
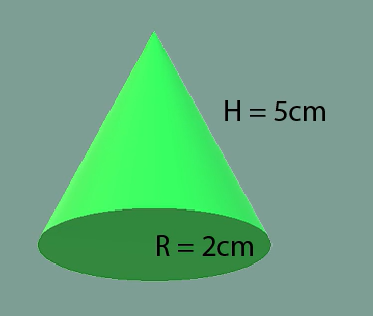
Here we can see that we have a height of 5 cm and a radius of 2 cm. Once we plug in all of our numbers, we have \(V=\frac{1}{3}(5cm)\pi (2)^{2}\). When solved, we have \(V=20.94cm^{3}\).
Great job, you guys. Learning new formulas can be hard. The important thing is to keep practicing so that you are able to recognize which formula you need to use and to memorize the formulas. I hope this was helpful. See you next time!
Frequently Asked Questions
Q
How do you find the volume of a triangular prism?
A
Find the volume of a triangular prism by multiplying the area of the base (the triangle part) by the height of the prism.
A = Bh
Ex. Find the volume of this triangular prism.
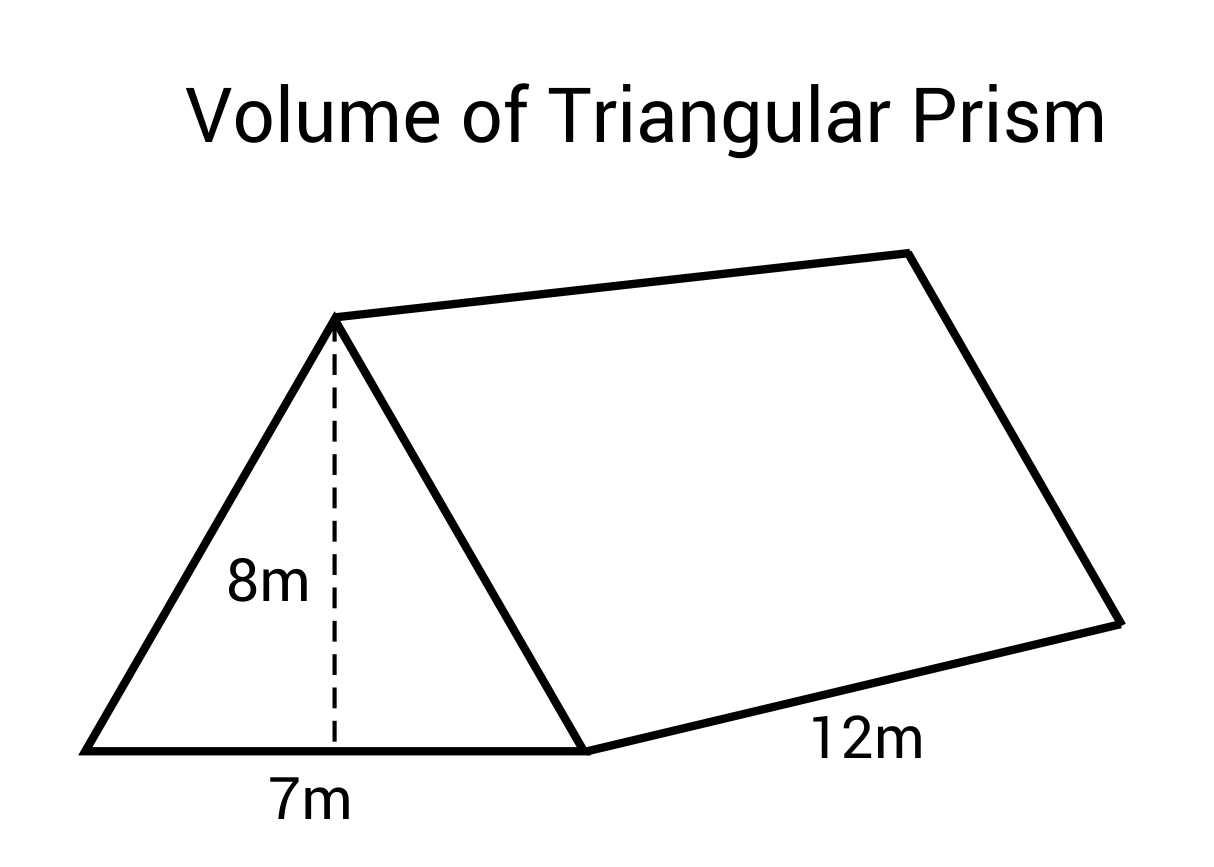
\(V=Bh=\frac{1}{2} (7)(8)(12)=336m^3\)
Q
How do you find the volume of a cube?
A
Find the volume of a cube by cubing its side length.
V=s3
Ex. What is the volume of a cube with a side length of 7 cm?
V = s3 = 73 = 343 cm3
Q
How do you find the volume of a rectangular prism?
A
Find the volume of a rectangular prism by multiplying its length times its width times its height.
V = lwh
Ex. What is the volume of this rectangular prism?
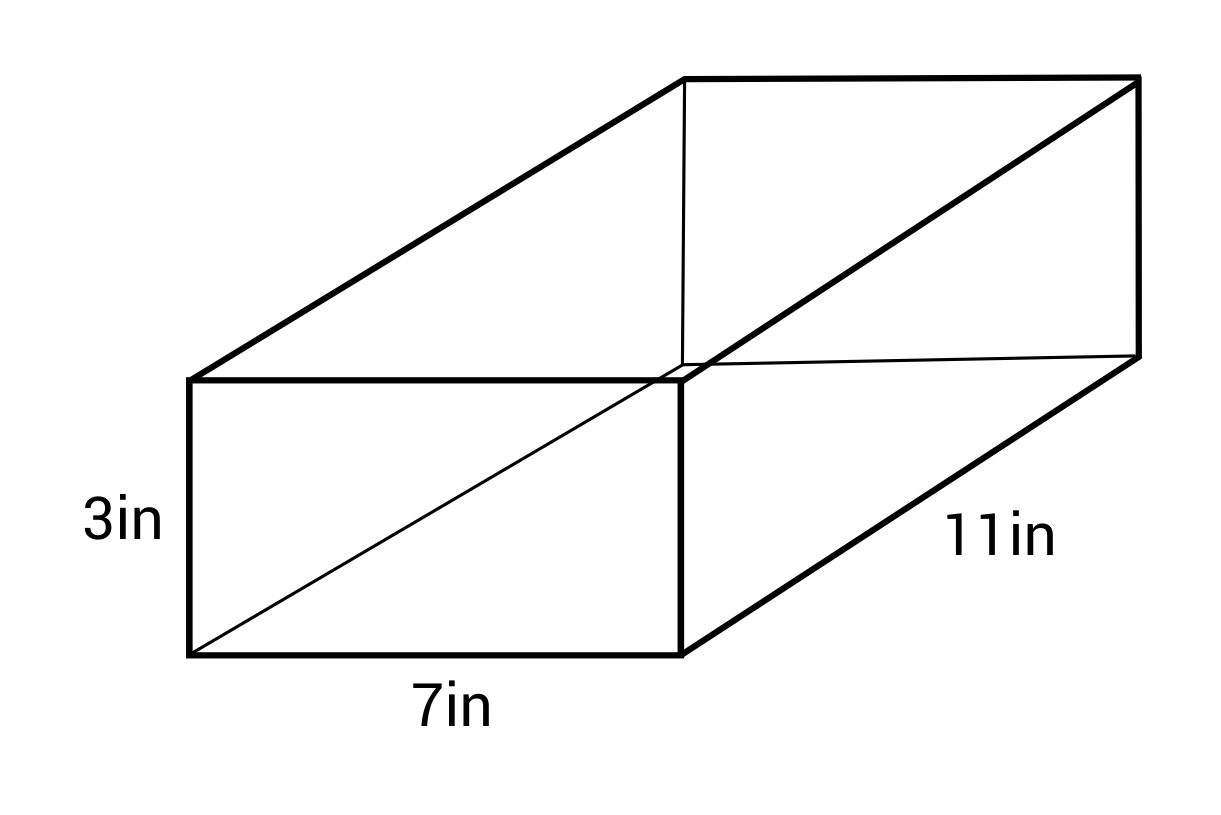
V = 3 × 7 × 11 = 231 in3
Q
How do you find the volume of a sphere?
A
Find the volume of a sphere by cubing its radius and multiplying by \(\frac{4}{3}\).
\(V=\frac{4}{3}πr^3\)
Ex. What is the volume of a sphere with radius 3 cm?
\(V=\frac{4}{3}π(3)^3=\frac{4}{3}π(27)=36πcm^3≈113.04cm^3\)
Q
How do you find the volume of a cone?
A
Find the volume of a cone by multiplying 1/3 times the area of the base times the height, or multiplying 1/3 times pi (π) times the radius squared times the height.
\(V=\frac{1}{3}Bh\) or \(V=\frac{1}{3}πr^2h\)
Ex. What is the volume of this cone?
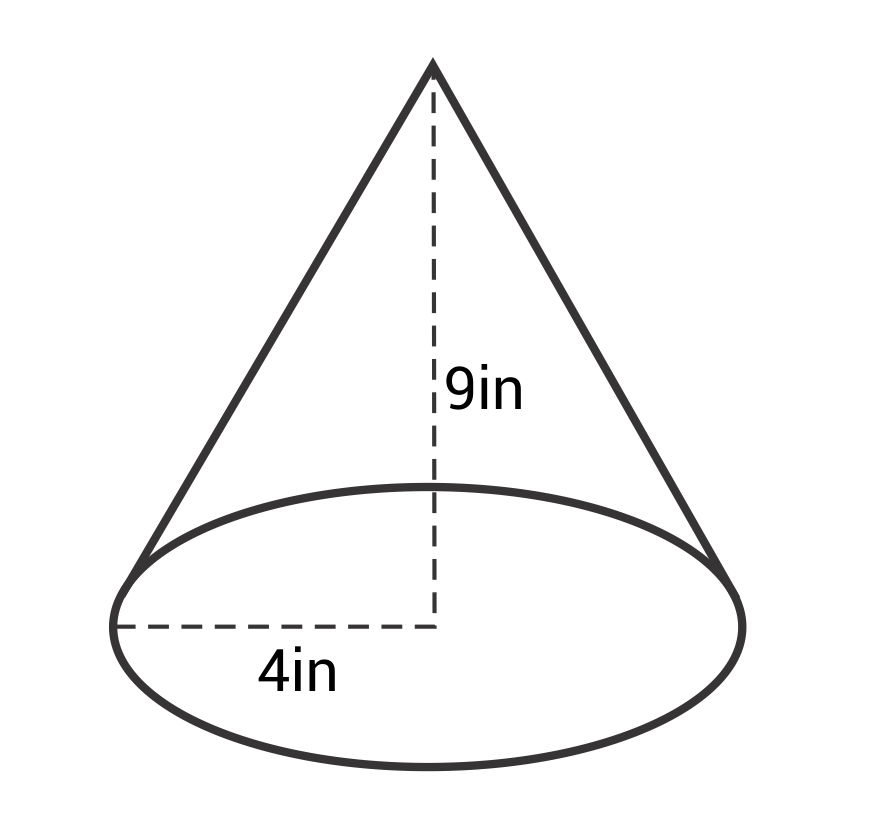
\(V=\frac{1}{3}π(4)^2(9)=48πin^2≈150.72in^2\)
Volume of 3D Objects Practice Questions
What is the volume of this rectangular prism?
112 cm3
153 cm3
198 cm3
220 cm3
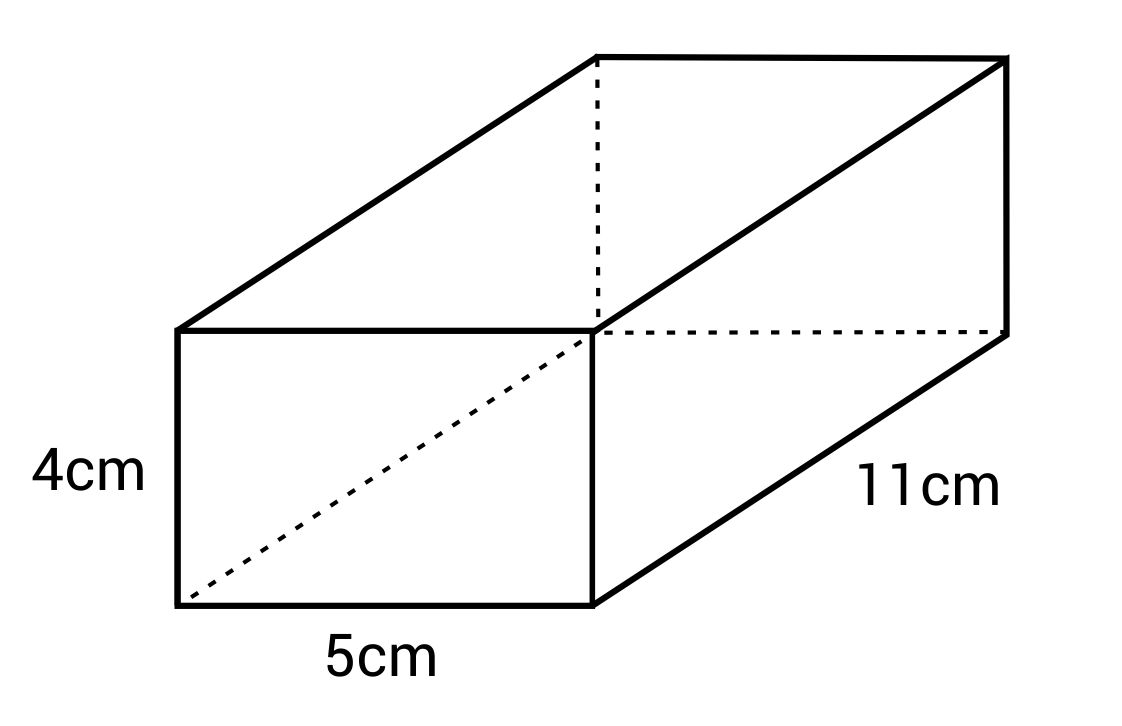
The correct answer is 220 cm3. The formula for volume of a rectangular prism is:
\(V=lwh\)
The length (l) is 5 cm. The width (w) is 4 cm. The height (h) is 11 cm.
\(V=(5)(4)(11)=220\text{ cm}^3\)
The volume of this rectangular prism is 220 cm3
What is the volume of a sphere with a 9-inch radius?
972.29 in3
2,513.06 in3
3,052.08 in3
4,179.14 in3
The correct answer is 3,052.08 in3. The formula for finding the volume of a sphere is:
\(V=\frac{4}{3}πr^3\)
The radius (r) is 9 inches.
\(V=\frac{4}{3}\pi(9)^3=\frac{4}{3}\pi(729)=972\pi≈3,052.08\text{ in}^3\)
The volume of this sphere is 3,052.08 in3.
What is the formula used to find the volume of a cone?
The correct answer is \(V=\frac{1}{3}πr^2h\). The general formula for the volume of a cone or pyramid is \(V=\frac{1}{3}Bh\), where B is the area of the base. Since the base of a cone is a circle and the area of a circle can be found using the formula \(A=πr^2\), substitute B with \(πr^2\) to get \(V=\frac{1}{3}πr^2h\).
What is the volume of this cone?
214.17 ft3
339.12 ft3
97.19 ft3
113.04 ft3
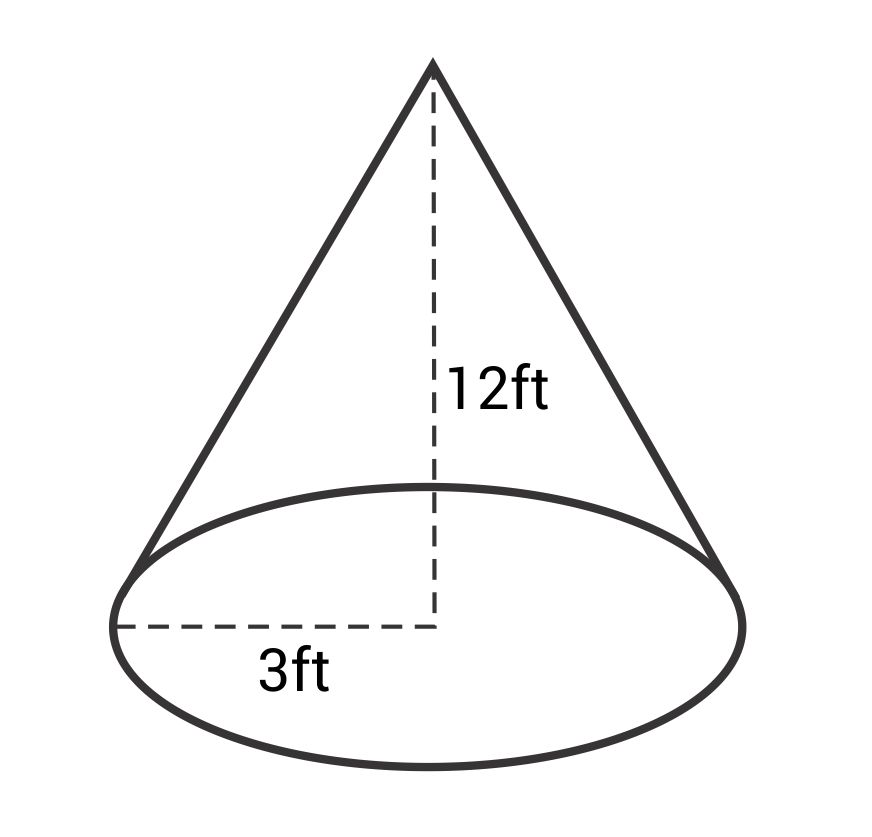
The correct answer is 113.04 ft3. The formula for volume of a cone is:
\(V=\frac{1}{3}πr^2h\)
The radius (r) is 3 ft and the height is 12 ft.
\(V=\frac{1}{3}\pi(3)^2(12)=36\pi≈113.04\text{ ft}^3\)
The volume of this cone is 113.04 cubic feet.
What is the volume of this triangular prism?
987 cm3
1,791.5 cm3
1,102.5 cm3
5,355 cm3
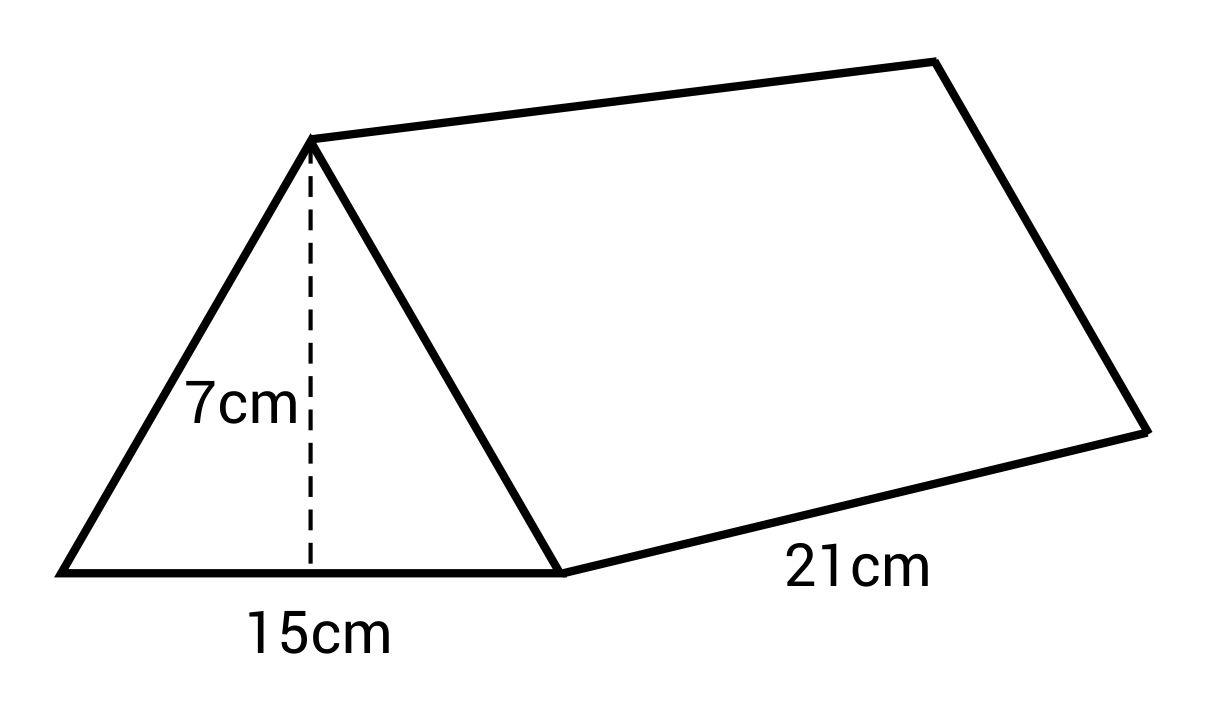
The correct answer is 1,102.5 cm3. The formula for the volume of a triangular prism is:
\(V=Bh\)
B stands for the area of the base, which in this case is a triangle. The formula for area of a triangle is \(A=\frac{1}{2}bh\). This can be substituted for B so the formula now looks like this:
\(V=\frac{1}{2}bh_Th\)
The height of the triangle has a subscript T so it can be distinguished from the height of the prism. The length of the base (b) is 15 cm. The length of the triangle’s height (hT) is 7 cm. The length of the prism height (h) is 21 cm.
\(V=\frac{1}{2}(15)(7)(21)=1,102.5\text{ cm}^3\)
The volume of this triangular prism is 1,102.5 cm3.