Finding the Volume and Surface Area of a Right Circular Cone

Hey guys! Welcome to today’s video where we’re going to talk about the volume and surface area of a cone. We know that a cone is actually a lot like a pyramid. While a pyramid has a square base that connects to a pointy tip at the opposite end, a cone’s base is, instead, a circle.

Before diving into the details, let’s make sure you’re comfortable with the concepts of volume and surface area. These are two key features that all \(3\)-dimensional shapes have. Volume is the space inside of a \(3D\) object, and surface area is, well, just that! It’s the total area of the surface of a shape. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. Every cube, sphere, cylinder, cone (of course), and so on has a volume and a surface area; and the formulas used for finding these measurements is different for each shape.

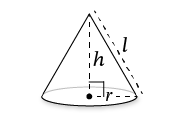
In the case of a cone, our volume formula looks like this:

\( V=\frac{1}{3}\pi r^{2}h\)

 
And our surface area formula looks like this:

\(SA=\pi r^{2}+\pi rl\)

 
Where \(r\), \(h\), and \(l\) represent different measurements on the cone. But which measurements do these letters (or, as we call them in the ‘math world,’ variables) represent?

The \(r\) represents the radius of the circular base of the cone.

The \(h\) represents the height of the cone. More specifically, it’s the length of an imaginary line that runs from the center of the circular base to the very tip of the cone.

Finally, the \(l\) represents the slant height. Think of this as a straight line that runs from the tip of the cone to the edge of its base.

So, to solve the volume and surface area equations, we’d simply plug a cone’s measurements into the respective variables. Let’s try a quick example.

Say we have a cone whose base radius measures \(3\) units, height measures \(4\) units, and slant height measures \(5\) units. First, let’s find its volume.

So, \(V=\frac{1}{3}\pi r^{2}h\). So we’re gonna rewrite this formula. We know our radius is equal to \(3\), so we’re gonna substitute \(3\) for our \(r\). And our height is equal to \(4\). So when we multiply this out, we get:

\(V=\frac{1}{3}\pi (9)(4)\)

 
Which is:

\(V=\frac{1}{3}\pi (36)\)

 
Which is equal to \(12\pi\). So the volume of this cone is \(12\pi\) (or approximately \(37.7\)) cubic units.

Notice that volume is measured in units cubed. Think centimeters cubed, inches cubed, feet cubed (or “cubic feet”), etc.

Okay, now let’s find the surface area of this little guy. So:

\(SA=\pi r^{2}+\pi rl\)

 
Then we’ll substitute in the numbers for our variables. So:

\(SA=\pi (3)^{2}+\pi (3)(5)\)

 
So:

\(SA=\pi(9)+\pi (15)\)

 
Which is equal to \(24\pi\). In the end, we’d say that the surface area is \(24\pi\) (or approximately \(75.4\)) square units. Notice the way that’s measured! Since we are talking about area, we use square units.

It’s pretty straightforward to plug in values for \(r\), \(h\), and \(l\), right? Well, what if we wanted to figure out what size ice cream cone we would need in order to fit \(30\) cubic inches of soft serve into it?

Because we can only have one unknown variable in an equation right now, and because we already know the volume of this cone (\(30\text{ in}^{3}\)), we’ll need to decide on a fixed value of either the cone’s height or the base’s radius. Let’s say that we want the cone to be exactly \(10\) inches in height (so \(h=10\text{ in}\)). Now all that’s left is to figure out what \(r\) equals! In other words, we need to find out how wide the opening of this cone gets.

First, we set up the volume equation using all the information we already have. So:

\(V=\frac{1}{3}\pi r^{2}h\)

 
And our volume is equal to \(30\) cubic inches. \(\frac{1}{3}\pi \) stays the same. We’re looking for \(r\), so we’re gonna leave that as \(r^{2}\), and \(h=10\text{ in}\).

\( 30=\frac{1}{3}\pi r^{2}(10)\)

 
So, if we rearrange a little, we’ll get this:

\(30=\frac{10}{3}\pi r^{2}\)

 
Now, we’re trying to get \(r\) all by itself on one side of the equals sign, so to do this, we’re gonna multiply both sides by \(\frac{3}{10\pi }\). When we do this, multiply by \(\frac{3}{10\pi }\) on the left, \(\frac{3}{10\pi }\) on the right:

\(\frac{3}{10\pi }\cdot 30=\frac{10}{3}\pi r^{2}\cdot \frac{3}{10\pi }\)

 
And that gives us:

\(\frac{90}{10\pi }=r^{2}\)

 
Then we can simplify this further to get:

\(\frac{9}{\pi }=r^{2}\)

 
Then, all we have to do is take the square root of both sides. So when we do this, we get:

\(r=\frac{3}{\sqrt{\pi }}\approx 1.7\)

 
In fact, since the linear dimensions of the cone are measured in inches, we know that \(r\) is approximately \(1.7\text{ inches}\).

Okay, cool! So what if we want to figure out the surface area of that cone we were just talking about? We now know the three important measurements of this cone: its volume, its height, and its base’s radius. Remember that in our surface area equation, we need both the radius and the slant height of the cone in order to find the surface area. Believe it or not, we can calculate the slant height by using the \(h\)-value that we were given and using the \(r\)-value that we just found. We just need to use the Pythagorean Theorem.

Let’s look at this particular cross-section of our cone:

Since this is a right triangle, we can use \(r^{2}+h^{2}=l^{2}\) to find the hypotenuse, which is the slant height. Let’s work that out. Remember, we just saw that \(r^{2}=\frac{9}{\pi }\). So we can substitute \(\frac{9}{\pi }\) in for \(r^{2}\). Plus \(h^{2}\), \(h\) is \(10\), \(10^{2}=100\), so plus \(100\). Equals \(l^{2}\), which we’re looking for \(l\).

\(\frac{9}{\pi }+100=l^{2}\)

 
Now we’re gonna want to simplify our addition on the left side. So we’re gonna keep \(\frac{9}{\pi }\) the same. And then we’re gonna need a common denominator for both of these parts, so we’re gonna do that by multiplying \(100\times \frac{\pi }{\pi }\). When we do that, we get \( \frac{100\pi }{\pi }\). Equals \(l^{2}\).

\(\frac{9}{\pi }+\frac{100\pi }{\pi }=l^{2}\)

 
Now we have the same denominator in both our fractions, so we can add them like normal.

\(\frac{9+100\pi }{\pi }=l^{2}\)

 
Now all that we have to do is take the square root of both sides. When we do this, we get that:

\(l\approx 10.1\)

 
So our slant height is approximately \(10.1\) inches.

Awesome! Now, let’s use this to find the surface area.

\(SA=\pi r^{2}+\pi rl\)

 
\(r\) is approximately \(1.7\).

\(SA=\pi (1.7)^{2}+\pi (1.7)(10.1)\)

 
Then, if you plug this into a calculator, you’ll get that:

\(SA\approx 63\text{ in}^{2}\)

And that’s it! By just knowing the cone’s volume and height, we were able to find its radius, its slant height, and its surface area.

I want to work on one more example together, but first, let me tell you about how ancient mathematicians came up with these volume and surface area formulas. Why do we divide \(\pi r^{2}h\) by \(3\) in the volume equation? And why are we only concerned with the \(r\)– and \(l\)-values when we find surface area?

To answer that first question, there’s one fact you need to know: a cone has a volume that’s \(\frac{1}{3}\) the size of a cylinder’s volume, as long as they have a same-sized circular base. Take a look:

The \(r\)– and \(h\)-values of these two objects are the same, and we know that the volume equation of a cylinder is \(V=\pi r^{2}h\). Hence, since this cylinder could hold \(3\) times the amount of stuff inside of it, we have that the volume of the cone is equal to \(\frac{\pi r^{2}h}{3}\).

As for the cone’s surface area, we need to consider the two different “sides” of this \(3D\) shape. We have a circle sitting on the bottom, and we have this curved surface connecting the base to the endpoint. So, we need to add the area of the circle (remember, that’s \(\pi r^{2}\)) to the area of the curved piece (which is \(\pi rl\)).

With all of this in mind, let’s look at our final example.

Say we have a huge cone whose base’s diameter measures \(10\) feet, height measures \(12\) feet, and would need a \(13\)-foot-long rope to connect a straight line from the tip to the edge of the base. We know how to find this cone’s surface area and volume.

First, let’s work on the volume! Again, we have that \(V=\frac{1}{3}\pi r^{2}h\). But, remember, we were given the diameter of the circular base, not its radius. We couldn’t just plug the \(10\) into the \(r\)’s place in that equation. Instead, we use what we know about the relationship between diameter and radius: a circle’s radius is \(\frac{1}{2}\) of its diameter. So this cone’s radius is actually \(5\) feet; and now finding the volume is pretty straightforward.

So if we plug in the variables that we know, we get:

\(V=\frac{1}{3}\pi (5)^{2}(12)\)
\(V=\frac{1}{3}\pi (25)(12)\)
\(V=\frac{1}{3}\pi (300)\)
\(V=100\pi \)

 
So the volume is \(100\pi \text{ ft}^{3}\).

Finally, let’s find the surface area.

\(SA=\pi r^{2}+\pi rl\)

 
When we plug in our known variables, we get:

\(SA= \pi (5)^{2}+\pi (5)(13)\)
\(SA=25\pi +65\pi \)

 
Which is equal to \( 90\pi \text{ ft}^{2}\). So we see that we’d need \( 90\pi \text{ ft}^{2}\) of wrapping paper to cover this thing!

Well, I hope that this has given you a greater understanding of cones and has made you confident in your ability to find any cone’s volume and surface area. Thanks for watching, and happy studying!

Frequently Asked Questions

Volume and Surface Area of a Right Circular Cone Practice Questions