Order of Operations (PEMDAS)
Imagine you’re getting ready for a walk. You grab your shoes and socks and head to the couch. Which do you put on first: shoes or socks? Of course, it’s your socks. That’s the correct order.
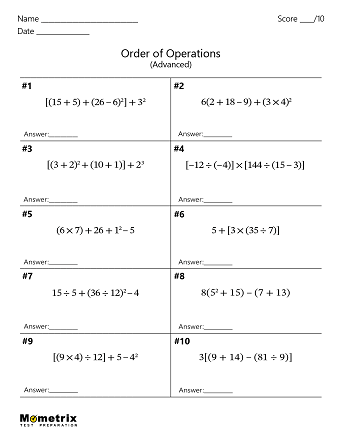
Now, imagine two friends attempting to simplify this expression: \(28 – 3 × 5 + 10\). The first friend simplifies the expression to 23, and the second friend simplifies the expression to 135. Who is right? The first friend. They remembered to use the order of operations. The second friend “tried to put the shoes on first,” meaning they computed the first operation they came across, giving them an incorrect result. Just like prepping for your walk, simplifying expressions requires a set order, also known as the order of operations.
PEMDAS Meaning
Many people use the acronym PEMDAS to help remember the order of operations. PEMDAS stands for “Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction.” The acronym also helps to remember that we start simplifying the expression from left to right, just like we read “PEMDAS” from left to right.
PEMDAS Examples
Let’s use PEMDAS to take a closer look at the order of operations.
\(28 – 3 × 5 + 10\)
Start by scanning the expression for “P” – parentheses. If you encounter a multiple-term expression inside the parentheses, continue to apply the same order of operations inside the parentheses to accurately simplify it before moving on to the next step. It’s worth noting that you should also look for brackets and braces in this step as well.
There are no parentheses in this expression, so we continue to the next operation: “E” for exponents.
Exponents can be found anywhere in the expression, including on the outside of parentheses. When this happens, be sure to compute what’s inside the parentheses before applying the exponent. There are no exponents in this expression, so we move on to the next step.
Now, we are looking for “MD” (either multiplication or division). Multiplication and division are inverse operations, so they are considered a set. This means we would use whichever operation comes first, from left to right.
This expression has a multiplication operator (\(3 × 5\)), so we compute that first: \(3 × 5 = 15\). To stay organized, we rewrite the expression below the original, showing our result for the first operation, \(28 – 3 × 5 + 10\) becomes \(28 – 15 + 10\).
We are ready to look for the last set of operations and finish simplifying this expression. The final set of operations “AS” – addition and subtraction. Just like multiplication and division, addition and subtraction are a set of inverse operations, so we treat them the same by using whichever operation comes first from left to right. In this expression, subtraction comes first, so we compute the subtraction, \(28 – 15 = 13\), and then compute the addition: \(13 + 10 = 23\).
Okay, before we work through some other problems, let’s review what PEMDAS stands for: Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. Follow this order of operations and complete any inverse operations (multiplication/division and addition/subtraction) from left to right.
Review
All right, let’s use PEMDAS to solve the following practice questions:
1. Use the order of operations to simplify this expression to three terms.
\((73 – 5^2 × 2) + 21 – 3\)
- \(5^2 × 2 +18\)
- \(73 – 50 +18\)
- \(23 + 21 -3\)
- \(48 + 21 -3\)
The first step when simplifying this expression is the exponent inside the parentheses.
\((73 – 5^2 × 2) + 21 – 3\)
\((73 – 25 × 2) + 21 – 3\)
Next is the multiplication inside the parentheses.
\((73 – 25 × 2) + 21 – 3\)
\((73 – 50) + 21 – 3\)
Finally, subtract inside the parentheses to simplify to three terms.
\((73 – 50) + 21 – 3\)
\(23 + 21 – 3\)
If you selected choice A or B, you subtracted too soon and did not compute inside the parentheses first. If you selected choice D, you did not use the order of operations inside the parentheses. The first step to simplifying this expression is to compute the exponent inside the parentheses, then multiply, and then subtract.
2. Look at the two simplifications for the expression.
\(45 – 6+(3^2+2)+14\)
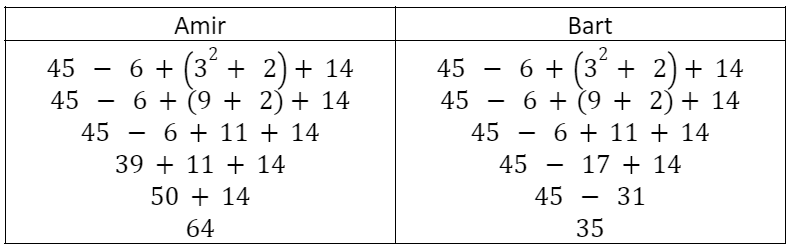
Which student is correct, and what mistake did the other student make?
- Amir, Bart did not add before subtracting.
- Amir, Bart did not subtract before adding
- Bart, Amir did not add before subtracting.
- Bart, Amir did not subtract before adding.
When computing addition and subtraction in an expression, always work from left to right and use the operation to the left first. In this expression, that is subtraction. So, Amir’s simplification is correct, and Bart added before subtracting.
That’s all for this review. Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is the order of operations in math?
A
The order of operations is the order you use to work out math expressions: parentheses, exponents, multiplication, division, addition, subtraction. All expressions should be simplified in this order. The only exception is that multiplication and division can be worked at the same time, you are allowed to divide before you multiply, and the same goes for addition and subtraction. However, multiplication and division MUST come before addition and subtraction. The acronym PEMDAS is often used to remember this order.
Ex. Use the order of operations to simplify the expression \(3×4^2+8-(11+4)^2÷3\).
Parentheses: \(3×4^2+8-(15)^2÷3\)
Exponents: \(3×16+8-225÷3\)
Multiplication/Division: \(48+8-75\)
Addition/Subtraction: \(-19\)
Q
Do you use the order of operations when there are no parentheses?
A
Yes, always use the order of operations to simplify expressions. If there are no parentheses, then skip that step and move on to the next one. The same applies for any other missing operation.
Ex.Use the order of operations to simplify the expression \(6^2-4+2\).
Parentheses: There are none, so skip this step.
Exponents: \(36-4+2\)
Multiplication/Division: There isn’t any, so skip this step.
Addition/Subtraction: \(34\)
Q
Do calculators do order of operations?
A
No, most calculators do not follow the order of operations, so be very careful how you plug numbers in! Make sure you follow the order of operations, even if that means plugging in numbers in a different order from how they look on your page.
Q
Which math operation comes first?
A
Parentheses are the first operation to solve in an equation. If there are no parentheses, then move through the order of operations (PEMDAS) until you find an operation you do have and start there.
Q
What are the basic operations?
A
The four basic operations are: addition (+), subtraction (-), multiplication (×), and division (÷).
Math Order of Operations Rules PDF
Order of Operations Practice Problems
\(7\times9+3-6\div2+2^2-11\)
The correct answer is 56. The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right.
\(7×9+3-6÷2+2^2-11\)
There are no parentheses in this problem, so start with exponents.
\(7×9+3-6÷2+4-11\)
Then, multiply and divide from left to right.
\(63+3-6÷2+4-11\)
\(63+3-3+4-11\)
Finally, add and subtract from left to right.
\(66-3+4-11\)
\(63+4-11\)
\(67-11\)
\(56\)
\(19+7(26-48÷2)^3+3×6\)
The correct answer is 93. The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right.
\(19+7(26-48÷2)^3+3×6\)
First, start with parentheses. The order of operations must be followed even inside parentheses, so be sure to divide before you subtract.
\(19+7(26-24)^3+3×6\)
\(19+7(2)^3+3×6\)
Next comes exponents.
\(19+7(8)+3×6\)
Then, multiply from left to right.
\(19+56+3×6\)
\(19+56+18\)
Finally, add from left to right.
\(75+18\)
\(93\)
\(11+3-7×2+1×4÷2\)
The correct answer is 2. The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right.
\(11+3-7×2+1×4÷2\)
There are no parentheses or exponents, so start with multiplication and division from left to right.
\(11+3-14+1×4÷2\)
\(11+3-14+4÷2\)
\(11+3-14+2\)
Finally, add and subtract from left to right.
\(14-14+2\)
\(0+2\)
\(2\)
\(3(11+2)^2-18÷6\)
The correct answer is 504. The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right.
\(3(11+2)^2-18÷6\)
First, simplify what is in parentheses.
\(3(13)^2-18÷6\)
Then, do any exponents.
\(3(169)-18÷6\)
Next, multiply and divide from left to right.
\(507-18÷6\)
\(507-3\)
Finally, subtract.
\(504\)
\((16-24)^2+3×11-1\)
The correct answer is 96. The order of operations can be remembered by the acronym PEMDAS, which stands for: parentheses, exponents, multiplication and division from left to right, and addition and subtraction from left to right.
\((16-24)^2+3×11-1\)
First, simplify the parentheses.
\((-8)^2+3×11-1\)
Then, do exponents.
\(64+3×11-1\)
Next, multiply.
\(64+33-1\)
Finally, add and subtract from left to right.
\(97-1\)
\(96\)
Order of Operations Worksheet
Use our free printable order of operations worksheets for additional practice!
