
Hi, and welcome to this video on finding the volume and surface area of a prism!
Key Terms to Remember
Before we jump into how to find the volume and surface area of a prism, let’s go over a few key terms that we will see in our formulas. The first word we need to define is base. The bases of a prism are the two unique sides that the prism is named for. For example, if you have a hexagonal prism, the bases are the two hexagons on either end of the prism.

The other word that will come up regularly in our formulas is height. Height is important to distinguish because it is different than the height used in some of our area formulas. The height of a prism is the length of an edge between the two bases.
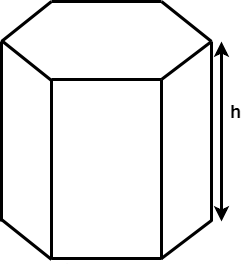
And finally, I want to review the word regular. Remember, regular in terms of polygons means that each side of the polygon has the same length.
Now that we have gone over some of our key terms, let’s look at our two formulas.
Rectangular Prism Volume Formula
To find the volume of a prism, multiply the area of the prism’s base times its height. This is written as \(V=Bh\). Notice that big B stands for area of the base. It is important that you capitalize this B because otherwise it simply means base. We see this in the formula for the area of a triangle, \(\frac{1}{2}bh\).
Rectangular Prism Surface Area Formula
The formula for the surface area of a prism is \(SA=2B+ph\), where \(B\), again, stands for the area of the base, \(p\) represents the perimeter of the base, and \(h\) stands for the height of the prism.
Now that we know what the formulas are, let’s look at a few example problems using them.
Example #1
Find the volume and surface area of this rectangular prism.
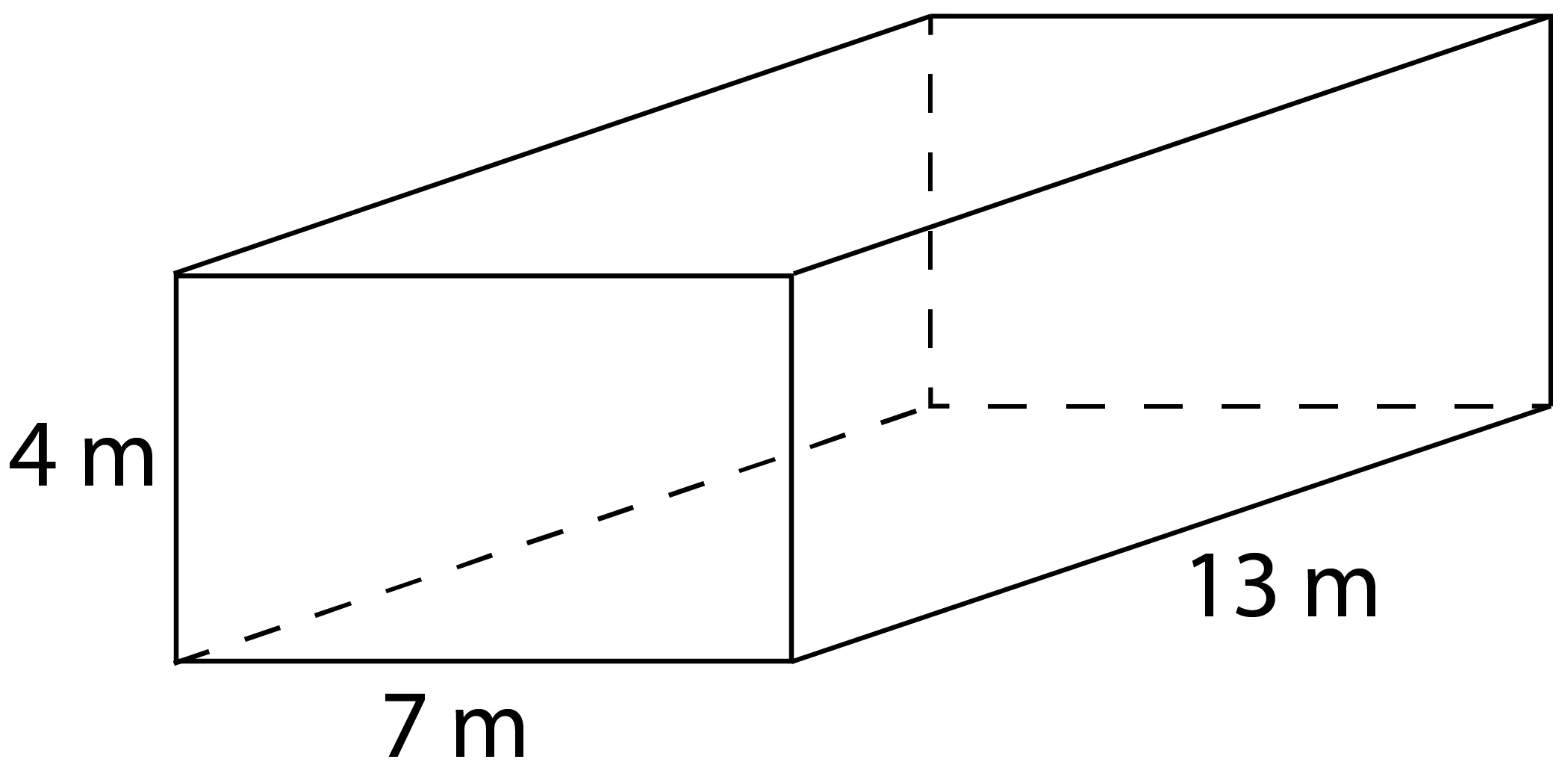
Let’s start with volume.
\(V=Bh\)
Since \(B\) stands for area of the base, we are going to substitute in the formula for area of a rectangle, length times width.
So \(V=lwh\)
Now, we are going to plug in our values.
\(V=4\times 7\times 13\)
When we multiply these out, this gives us \(364 m^3\). Remember, since we are multiplying by three dimensions, our units are cubed.
Now let’s look at our surface area.
\(SA=2B+ph\)
Again, we are going to substitute in our formula for area of a rectangle, and we are also going to substitute in our formula for perimeter of a rectangle.
\(SA=2lw+2(l+w)h\)
Now we can plug in our known values.
\(SA=2(13\times 7)+2(13+7)(4)\)
And we simplify to get our answer.
\(SA=2(91)+2(20)×4\)
\(=182+160\)
\(=342\text{ m}^2\)
The surface area is 342 meters squared.
Remember, with surface area, we are adding the areas of each face together, so we are only multiplying by two dimensions, which is why we square our units.
Example #2
Let’s try another example.
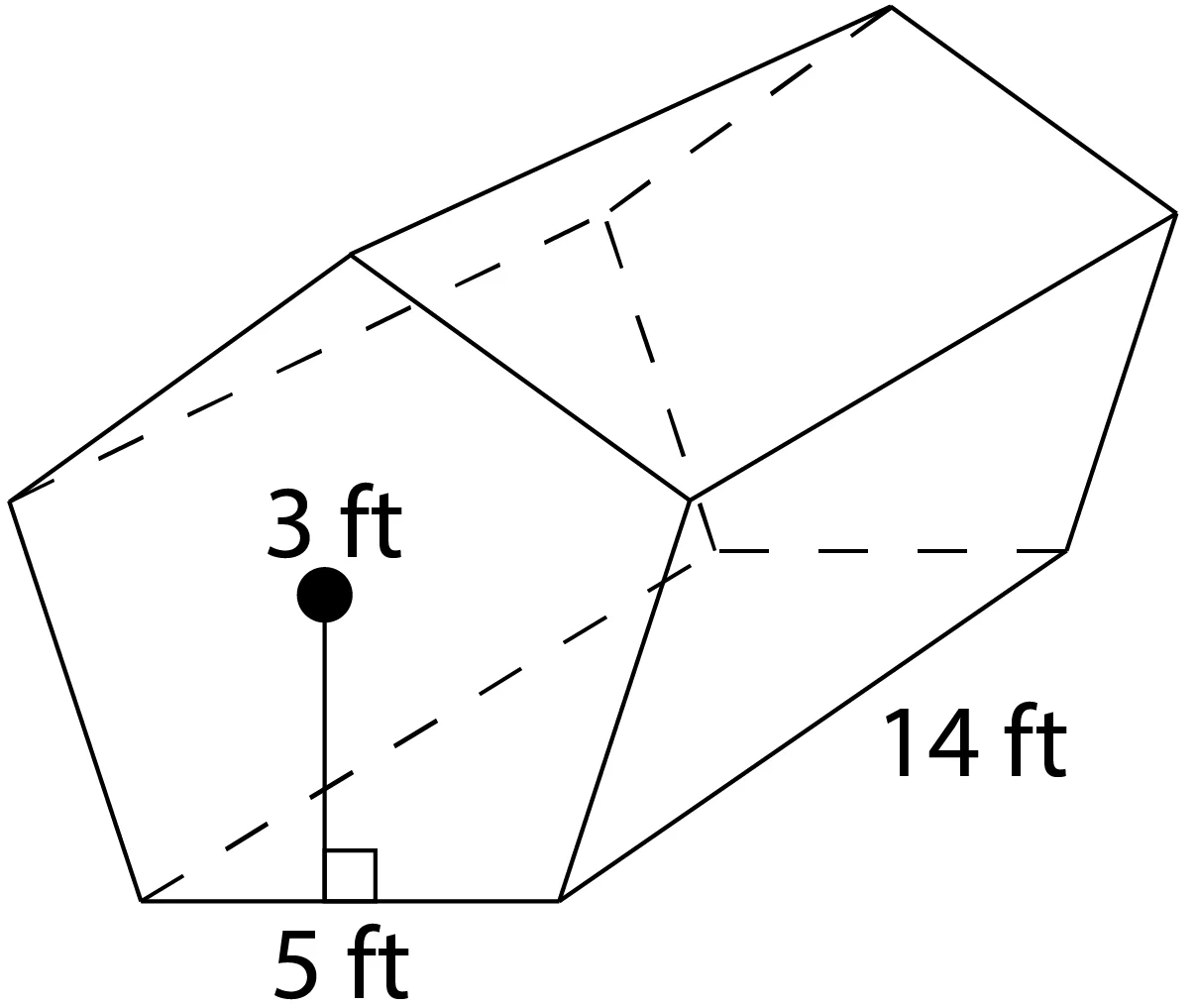
Find the volume and surface area of this regular pentagonal prism.
Let’s start with our volume.
\(V=Bh\)
We want to substitute in our formula for the area of a regular pentagon. This formula isn’t common, so it’s okay if you need to look it up.
The area of a regular pentagon is found by \(V=(\frac{1}{2}pa)h\)
Now we can plug in our values. Remember, regular means that all the sides of the pentagon are congruent, so we can find our perimeter by multiplying our side value by 5.
\(V=(\frac{1}{2}\times 5\times 5\times 3)(14)\)
Which, when we multiply this out, gives us 525 cubic feet.
Now let’s move on to surface area.
\(SA=2B+ph\)
First, we want to substitute in our formulas.
\(SA=2(\frac{1}{2}pa)+(5s)h\)
And now we plug in our values.
\(SA=2(\frac{1}{2}\times 5\times 5\times 3)+(5\times 5)(14)\)
\(=75+350\)
\(=425\text{ ft}^2\)
The surface area of our prism is 425 square feet.
Example #3
Let’s look at one more example, but this time I want you to try it on your own.
Find the volume and surface area of this regular triangular prism.
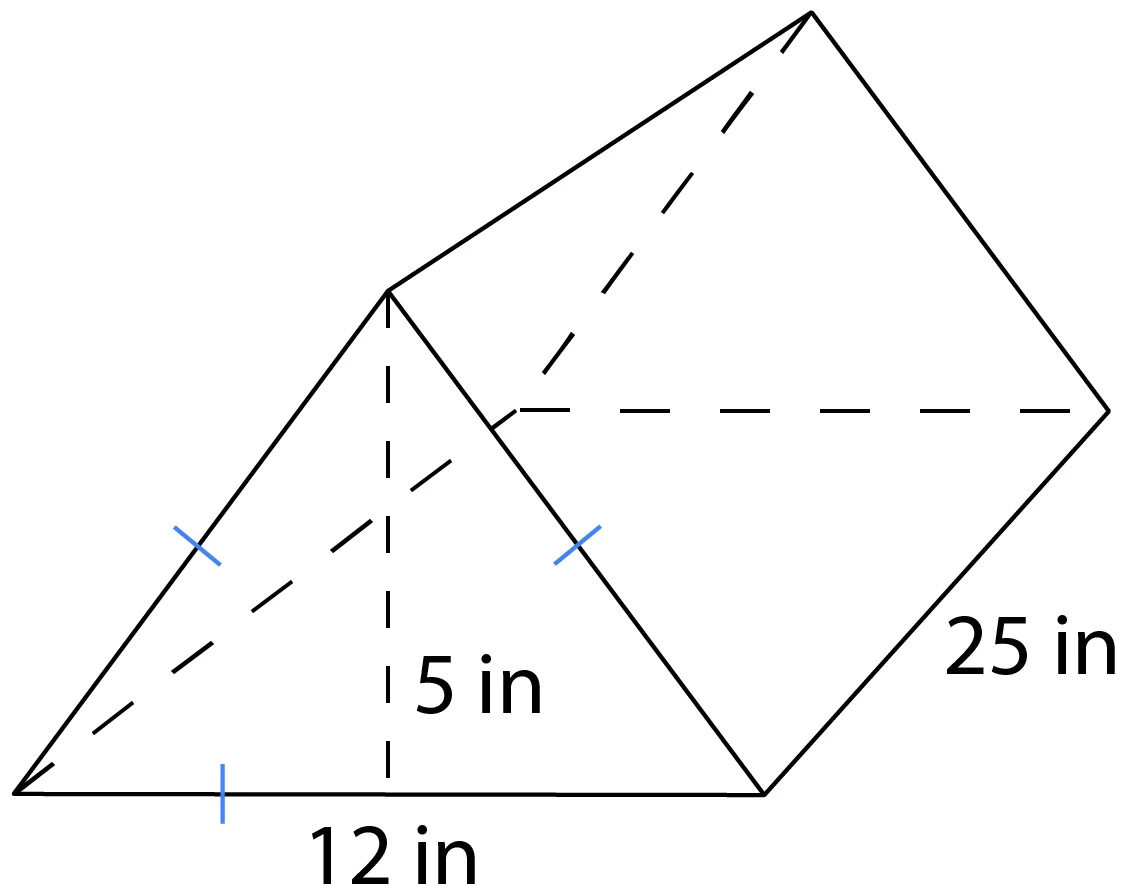
Pause the video and see if you can come up with the answers on your own. Then check them with mine.
Ready to check?
Let’s look at volume first.
\(V=Bh\)
We substitute in our formula for area of a triangle.
\(V=(\frac{1}{2}bh_T)h\)
Notice that I put a \(T\) on the height of the triangle to distinguish it from the height of the prism.
Now let’s plug in our values.
\(V=(\frac{1}{2}\times 12\times 5)(25)=750 in^3\)
The volume of our triangular prism is 750 cubic inches.
Now onto surface area.
\(SA=2B+ph\)
First, substitute in your formulas.
\(SA=2(\frac{1}{2}bh)+(3s)h\)
We can use 3s for the perimeter because it is a regular triangle, or an equilateral triangle, so all the sides are the same length.
Now, we plug in our values and solve.
\(SA=2(\frac{1}{2}\times 5\times 12)+(3\times 12)(25)=60+900=960\text{ in}^2\)
The surface area of our triangular prism is 960 square inches.
And that’s all there is to it! I hope this review of the volume and surface area of prisms was helpful. Thanks for watching and happy studying!
Volume and Surface Area of a Prism Practice Questions
Find the volume of the rectangular prism shown below:
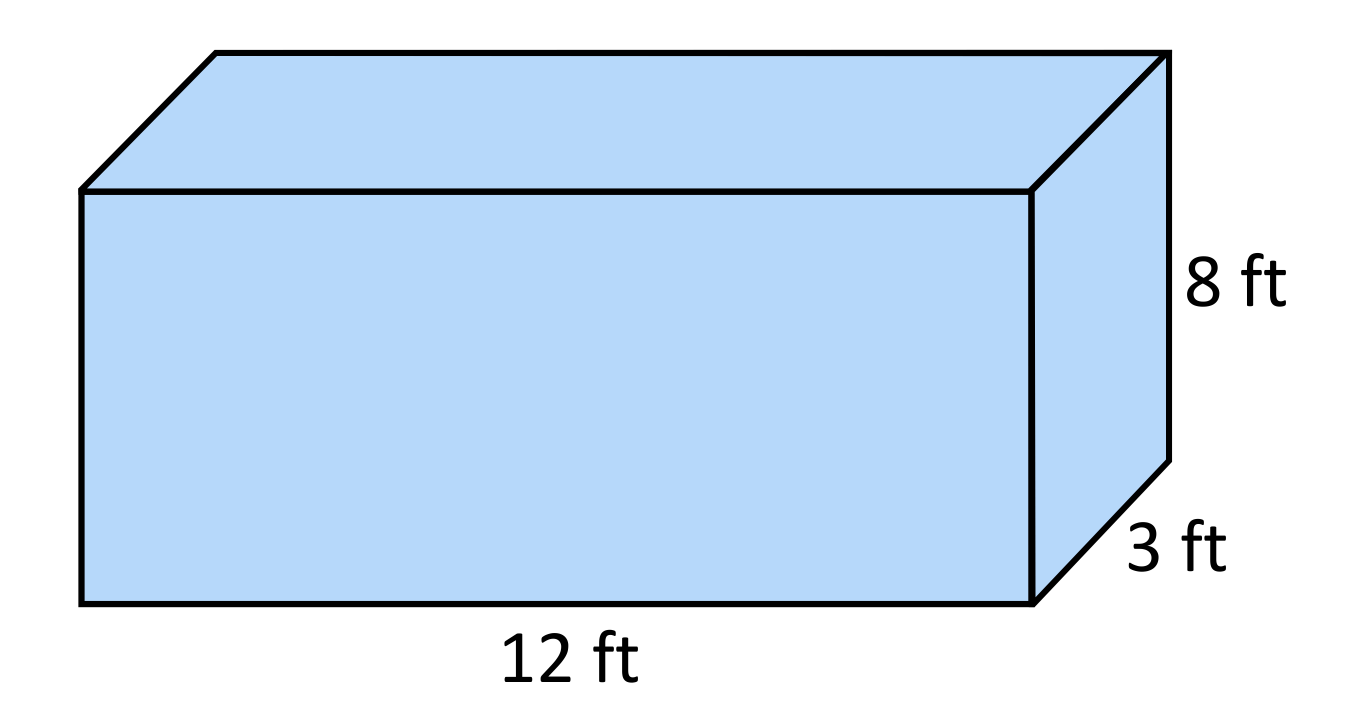
| \(V=Bh\) | To find the volume of a prism, use the formula \(V=Bh\), where \(V\) stands for volume, \(B\) stands for the area of the base of the prism, and \(h\) stands for its height. |
| \(V=(lw)h\) | Since this is a rectangular prism, substitute the area formula of a rectangle for \(B\). The area of the base of the prism is equal to \(lw\), which is the length times the width. |
| \(V=(8\times3)(12)\) | From here, replace the variables with their corresponding values. The length of the base is \(8\) feet, the width of the base is \(3\) feet, and the height of the entire rectangular prism is \(12\) feet. |
| \(V=(24)(12)\) | Next, simplify expressions in parentheses. Since \(8\times3=24\), rewrite the equation using this product. |
| \(V=288\text{ ft}^3\) | Multiply \(24\) by \(12\) to find the volume of the prism. \(24\) times \(12\) equals \(288\), so the volume of the rectangular prism is \(288\text{ ft}^3\). Therefore, answer A is correct. |
Find the surface area of the rectangular prism shown below:
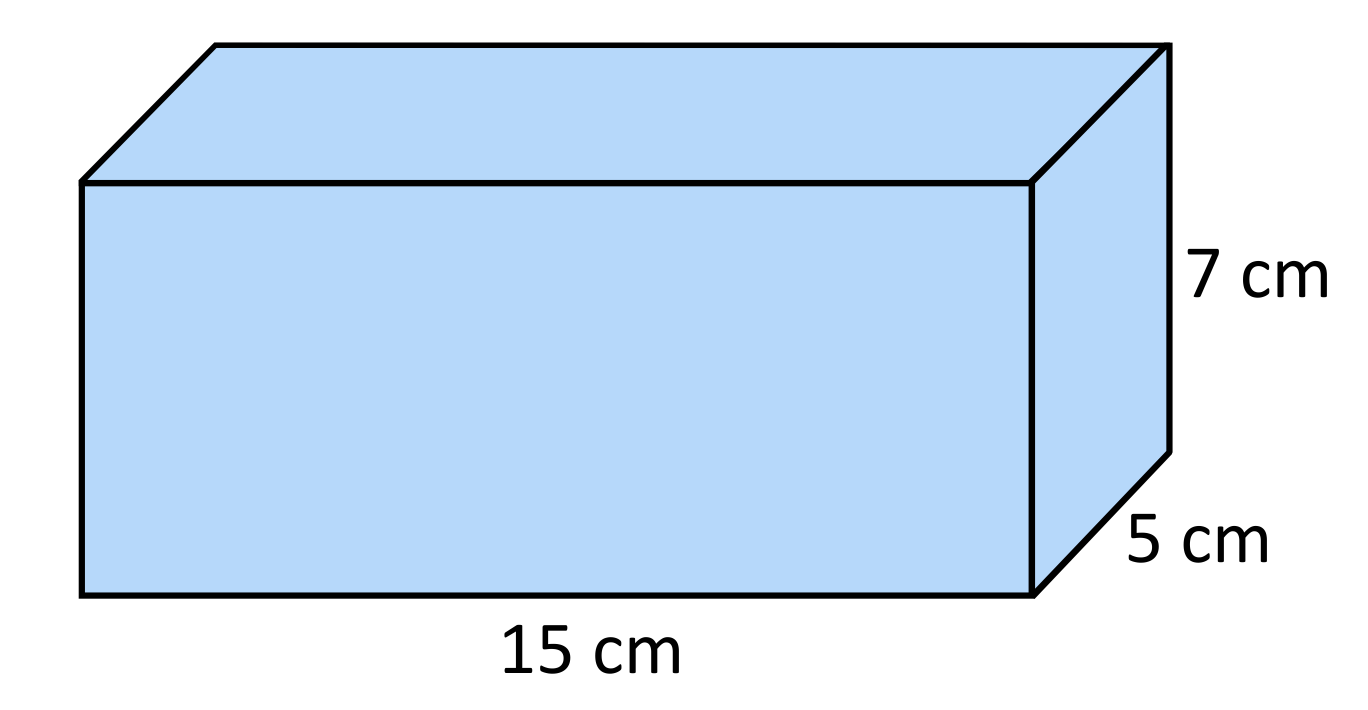
| \(SA=2B+ph\) | To find the surface area of a prism, use the formula \(SA=2B+ph\), where \(SA\) stands for surface area, \(B\) stands for the area of the base of the prism, \(p\) stands for the perimeter of the base, and \(h\) stands for height of the prism. |
| \(SA=2(lw)+2(l + w)h\) | Since this is a rectangular prism, substitute the area formula of a rectangle for \(B\). The base of the prism is equal to \(lw\), which is the length times the width. Next, substitute the perimeter formula of a rectangle for \(p\). The perimeter of a rectangle is equal to \(2(l+w)\), which is \(2\) times the length plus the width. |
| \(SA=2(7\times5)+2(7+5)(15)\) | From here, replace the variables with their corresponding values. The length of the base is \(7\) centimeters, the width of the base is \(5\) centimeters, and the height of the entire rectangular prism is \(15\) centimeters. |
| \(SA=2(35)+2(12)(15)\) | Next, simplify expressions in parentheses. Since \(7\times5=35\), rewrite the equation with this product. Since \(7+5=12\), rewrite the equation using this sum. |
| \(SA=70+2(12)(15)\) | From here, use the order of operations to solve. Multiply each expression from left to right. Since \(2(35)=70\), rewrite the equation with this product. |
| \(SA=70+360\) | Next, simplify \(2(12)(15)\). Since \(2(12)(15)=360\), rewrite the equation using this product. |
| \(SA=430\text{ cm}^2\) | From here, add \(70\) and \(360\) to find the surface area. \(70+360=430\), so the surface area of the rectangular prism is \(430\text{ cm}^2\). Remember that surface area refers to the total area that the surface of the rectangular prism occupies. Since this is two-dimensional, the final answer is raised to the second power, or “squared”. Therefore, answer C is correct. |
A pentagonal prism has a height of \(10\) meters, a perimeter of \(30\) meters, and its apothem is \(2\) meters. Based on this information, find the volume of the pentagonal prism.
| \(V=Bh\) | To find the volume of a prism, use the formula \(V=Bh\), where \(V\) stands for volume, \(B\) stands for the area of the base of the prism, and \(h\) stands for its height. |
| \(V=(\frac{1}{2}pa)h\) | Since this is a pentagonal prism, substitute the area formula of a pentagon for \(B\). The area of the base of the prism is equal to \((\frac{1}{2} pa)\), which is \(\frac{1}{2}\) of the perimeter of the pentagon times the apothem. |
| \(V=(\frac{1}{2}\times30\times2)(10)\) | From here, replace variables with the corresponding values given in the problem. The perimeter of the base is \(30\) meters, the apothem is \(2\) meters, and the height of the entire pentagonal prism is \(10\) meters. |
| \(V=(30)(10)\) | Next, simplify expressions in parentheses. Since \((\frac{1}{2}\times30\times2)=30\), rewrite the equation using this product. |
| \(V=300\text{ m}^3\) | Multiply 30 by 10 to find the volume of the prism. \(30\) times \(10\) equals \(300\), so the volume of the pentagonal prism is \(300\text{ ft}^3\). Therefore, answer B is correct. |
Jake works for an outdoor recreation company that makes canvas tents for camping. Jake’s job is to purchase the exact amount of canvas needed for each tent. The tent he is working on is in the shape of a congruent triangular prism, as shown below. It has a base of 13 feet, a height of 8 feet, and a depth of 25 feet. Based on this information, find the surface area of the tent to figure out how much canvas Jake needs to purchase.
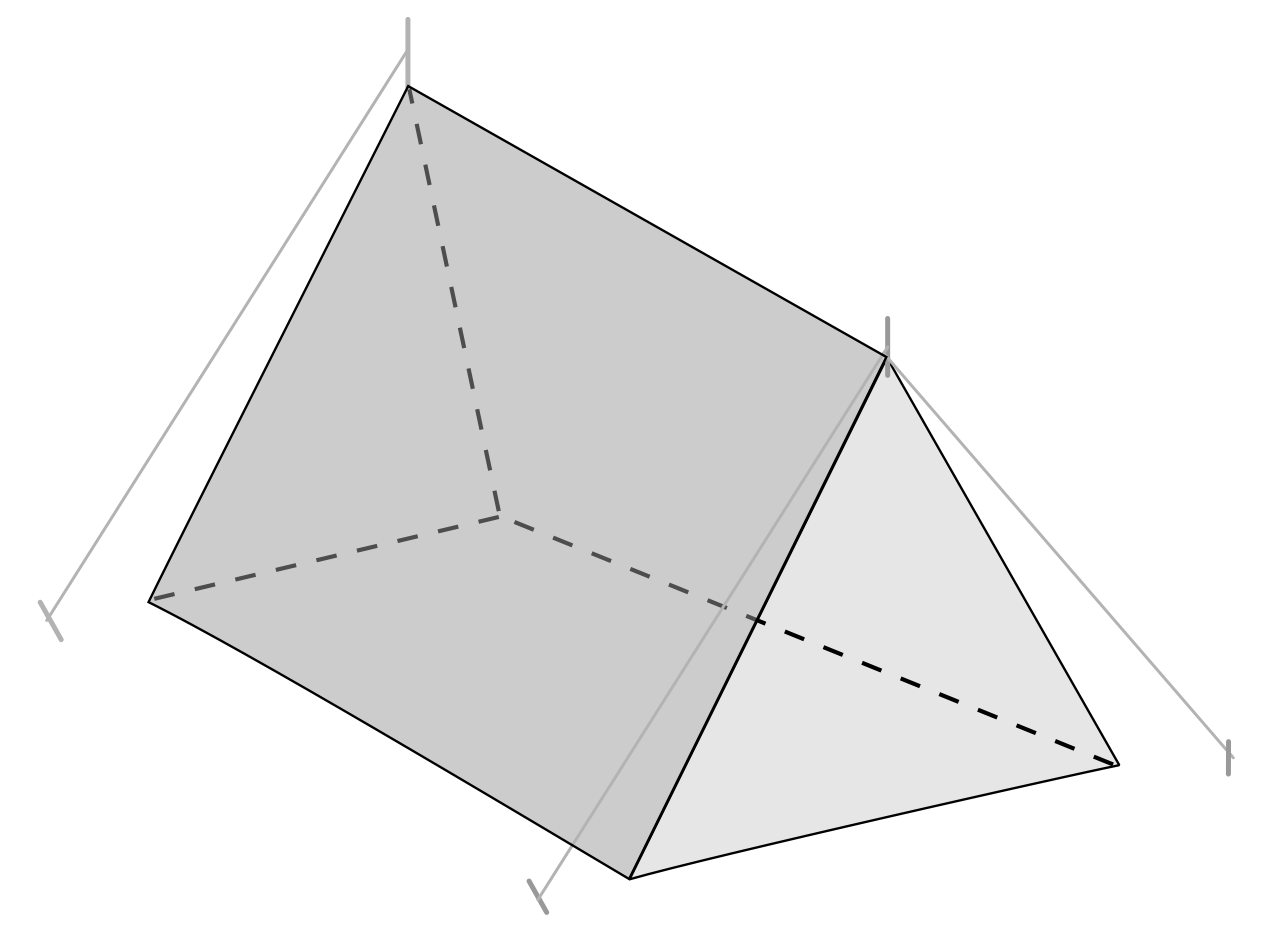
| \(SA=2B+ph\) | To find the surface area of a prism, use the formula \(SA=2B+ph\), where \(SA\) stands for surface area, \(B\) stands for area of the base of the prism, \(p\) stands for the perimeter of the base, and \(h\) stands for the height of the prism. |
| \(SA=2(\frac{1}{2}bh_t)+(3s)h\) | Since this is a triangular prism, substitute the area formula of a triangle for \(B\). The area of the base of the prism is equal to \(\frac{1}{2}bh_t\), which is one-half of the base times the height of the triangle. Next, substitute the perimeter formula of a triangle for \(p\). Since the triangle is congruent, meaning all sides are the same, the perimeter is equal to \(3s\), which is \(3\) times the length of one side. |
| \(SA=2(\frac{1}{2}\times13\times8)+(3\times13)(25)\) | From here, replace variables with the corresponding values given in the triangular prism shown. The length of the base is \(13\) feet, the height of the triangular base is \(8\) feet, each side of the base is \(3\) feet, and the height of the entire triangular prism is \(25\) feet. |
| \(SA=2(52)+(39)(25)\) | Next, simplify the expressions in parentheses. Since \((\frac{1}{2}\times13\times8)=52\), rewrite the equation using this product. Since \((3\times13)=39\), rewrite the equation using this product. |
| \(SA=104+975\) | From here, use the order of operations to solve. Multiply each expression from left to right. Since \(2(52)=104\), rewrite the equation with this product. Since \((39)(25)=975\), rewrite the equation using this product. |
| \(SA=1{,}079\text{ ft}^2\) | From here, add \(104\) and \(975\) to find the surface area. \(104+975=1{,}079\), so the surface area of the triangular prism is \(1{,}079\text{ ft}^2\). Therefore, answer D is correct. |
A wooden wedge in the shape of a triangular prism is being used as a doorstop. Its base is \(2\) inches, its height is \(1.5\) inches, and its depth is \(4\) inches. Based on this information, what is the volume of the doorstop?
| \(V=Bh\) | To find the volume of a prism, use the formula \(V=Bh\), where \(V\) stands for volume, \(B\) stands for the area of the base of the prism, and \(h\) stands for its height. |
| \(V=(\frac{1}{2}bh_t)(h)\) | Since this is a triangular prism, substitute the area formula of a triangle for \(B\). The base of the prism is equal to \((\frac{1}{2}bh_t)\), which is \(\frac{1}{2}\) of the base of the triangle times its height. |
| \(V=(\frac{1}{2}\times2\times1.5)(4)\) | From here, replace variables with the corresponding values given in the problem. The base of the triangle is \(2\) inches, the height is \(1.5\) inches, and the height, or depth, of the entire triangular prism is \(4\) inches. |
| \(V=(1.5)(4)\) | Next, simplify expressions in parentheses. Since \((\frac{1}{2}\times2\times1.5)=1.5\), rewrite the equation using this product. |
| \(V=6\text{ in}^3\) | Multiply \(1.5\) by \(4\) to find the volume of the prism. \(1.5\) times \(4\) equals \(6\), so the volume of the triangular prism is \(6\text{ in}^3\). Therefore, answer C is correct. |