The Diameter, Radius, and Circumference of Circles
Hey guys! Welcome to this video on the radius, diameter, and circumference of a circle.
Circles have been around for as long as the Earth has been around. People were able to see natural circles by observing the moon, the sun, and other various naturally circular shapes.
The first technological invention using a circular shape, however, wasn’t until 3500 BC, and it was the invention of the potter’s wheel. Then, 300 years later, they were used for the wheels of chariots. As people began to see the value and use for circular-shaped objects, they begin to study circles.
Things like radius, diameter, and circumference are terms that helps us to keep track of various measurements of a circle.
So, now, let’s take a look what each of these measurements represent.
Midpoint of a Circle
First, let’s define midpoint, so you’ll understand what I’m talking about as I reference it. Here’s a circle:
The midpoint is the exact center of the circle, where the dot is.
Radius vs. Diameter
Radius of a Circle
Radius is the length from the midpoint of the circle to the outer edge of the circle. The radius is represented by the lowercase letter \(r\).
Diameter of a Circle
Diameter is the full length of the circle running from the edge, through the midpoint, all the way to the other side. That is this whole length right here. The diameter of a circle is represented by the letter \(d\).
Circumference of a Circle
Now, circumference is the distance around the outside edge of this circle. Circumference is represented by the uppercase letter \(C\).
Circumference is comparable to the perimeter of a shape, like a parallelogram. If you were to cut the line of a circle, as if it were a string, and lay it out to measure. This length would be equivalent to the circumference. However, since a circle has a continuous curve, we use the word circumference rather than perimeter to distinguish it.
Now that we’ve looked at what the radius, diameter, and circumference are, let’s look at how to calculate each one.
Calculations
If someone were to just kinda hand you a piece of paper with a circle on it…. Well, actually, that would be pretty weird.
But let’s say we wanted to find the radius, diameter, and circumference of that circle, and all we have is a ruler.
The easiest thing to start with would be to take the ruler and measure, from the very center of the circle, the length between the outer edge. That would be the diameter.
Let’s say, that when we measured, we got a length of 9 cm for the diameter.
Well, we know that if our radius runs from the midpoint to the outer edge, then all we have to do to find the length of our radius would be to divide the length of the diameter by 2.
So, when we take 9 and divide it by 2 we get a radius length of 4.5 cm.
Radius Formula
The formula for the radius can be written as \(r=\frac{d}{2}\)
Diameter Formula
The formula for diameter can be written as \(d=2r\)
Circumference Formula
The formula for the circumference of a circle is \(C=\pi \times d\), or it can be written as \(C=2\times \pi \times r\). Either one works!
Now, you may be asking, “Well where did pi come from, and why do we all the sudden get the circumference if we multiply said pi by our diameter? Who decided that?” If you are not asking that question… You should, and I’m going to answer it anyways.
Pi is a symbol we use in mathematics to represent the number 3.14. And actually that is just pi rounded to the nearest hundredth. Pi actually has no end, and no predictable pattern. It just keeps going.
However, when you see the symbol \(\pi\), generally (and in our case), 3.14 will suffice.
Pi is not a random number that mathematicians made up, and declared “we will multiply the diameter by the number every time, and call it a circumference.” On the contrary, pi was discovered to be the constant ratio between the circumference and the diameter.
That is why and how we got the formula for the circumference of a circle.
Now, let’s take the circle with the diameter of 9 cm, and radius of 4.5 cm, and calculate the circumference.
I’m going to use the formula with the diameter for this one.
So, circumference equals (I’m just gonna rewrite the formula to help us follow our work), \(C=\pi \times d\), equals pi times diameter. So now all we need to do is to plug in our number for diameter.
\(C=(3.14)(9\text{ cm})=28.26\text{ cm}\)
And here’s our answer! Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. Then, find your radius, and circumference.
I hope that this video has been helpful for you.
See you guys next time!
Frequently Asked Questions
Q
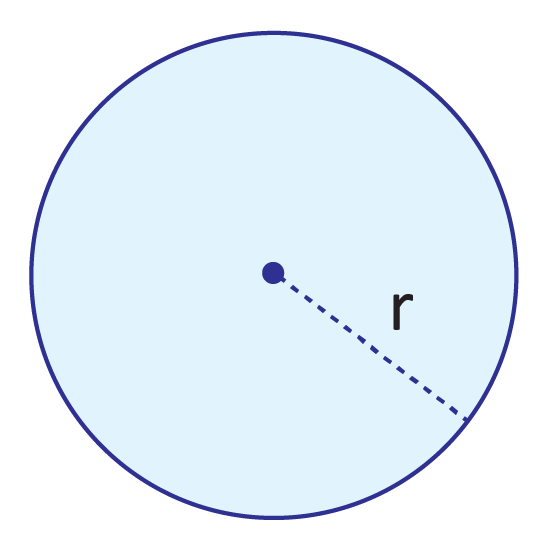
What is the radius of a circle?
A
If we were to measure the distance running from the center of a circle to the outer edge of said circle, we would be finding the radius. Think of a clock; if one of the hands was long enough to reach to the edge of the clock, this hand could be considered the radius of the clock – no matter what time it is!
Q
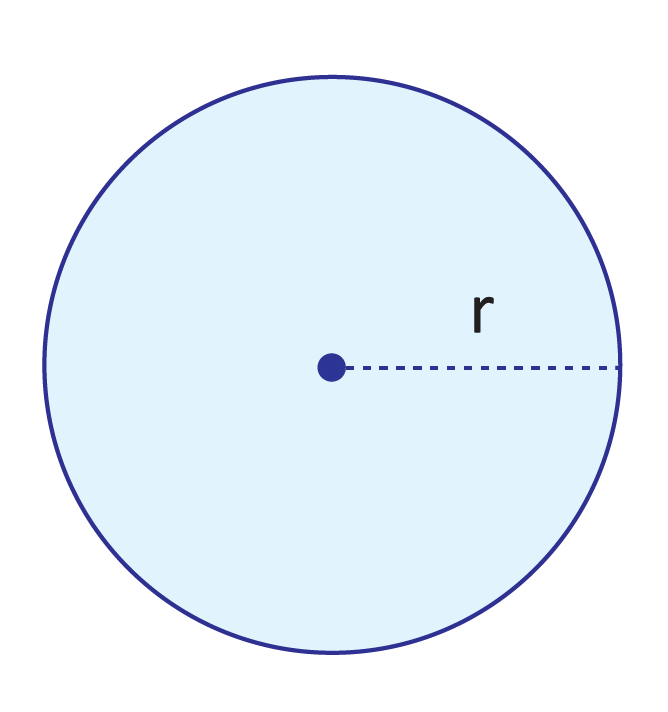
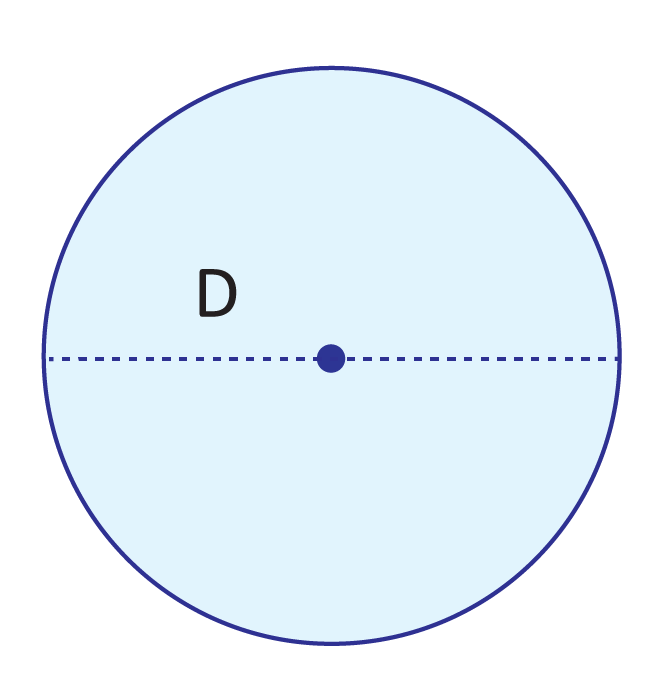
What are radius and diameter?
A
While the radius of a circle runs from its center to its edge, the diameter runs from edge to edge and cuts through the center. A circle’s diameter essentially splits the shape in half. Radius and diameter are close friends – a circle’s radius is half the length of its diameter (or: a circle’s diameter is twice the length of its radius).
Q
How is a radius named?
A
A radius is a line segment. Hence, it has two endpoints: the point at the center of the circle and the point along the circle’s edge which we’ve connected it to. With all of this in mind, we know to name a radius in the same way that we do all line segments: the name of both endpoints listed side-by-side (often with a bar above the two letters).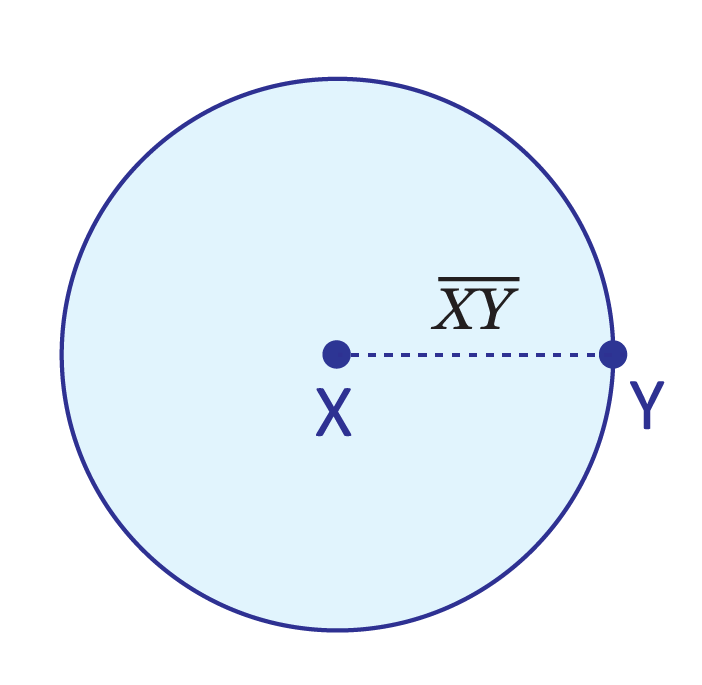
Q
Is a radius half the diameter?
A
Yes! If you remember only one fact about circles, let this one be it. Drill it into your mind! A radius is half the length of the diameter.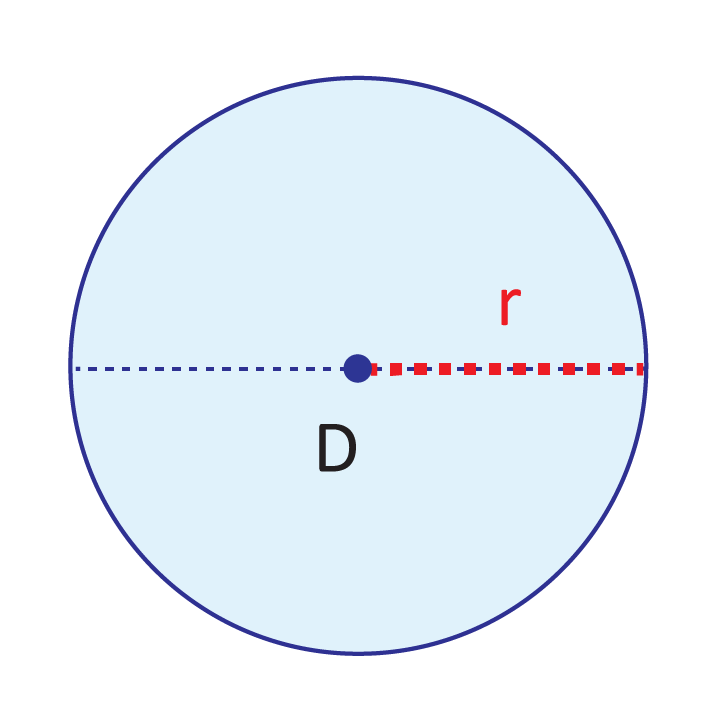
Q
How do you solve for radius and diameter?
A
If we only know the radius of a circle, we’ll just multiply that value by 2 in order to get the diameter \((d=2r)\). Similarly, if we only know the diameter of a circle, we divide by 2 and out pops the radius \((r=\frac{d}{2})\)!
But, what if we aren’t given either of these values? In order to solve for either the radius or diameter of a circle, we need to know either its circumference or its area.
Say that we were given the circumference. Since the equation for finding circumference looks like \(C=2πr\), we’ll just rearrange the equation and find:\(r=\frac{C}{2π}\).
If we were given the area, we’d rearrange its equation, \(A=πr^2\), to be: \(r=\sqrt{\frac{A}{π}}\)
Here’s an example: Given that the area of a circle is \(9π\text{ in}^2\), find its diameter. We know that the area equation is \(A=π×r^2\), but notice that there is not a ‘diameter’ variable in this formula. To solve this problem, we’ll either need to: (a.) replace \(\frac{d}{2}\) for r in the area equation, or (b.) find the value of r and then multiply that by 2. Here we’re going to use option b, but both methods are valid choices!
\(A=9π=πr^2\)
\(9=r^2\)
\(±3=r\)
(Notice that the square root of 9 can be either 3 or -3. Since we’re dealing with a real circle, we’ll simply use \(d=2r=6\text{ inches}\)
Q
How do you calculate the circumference of a circle?
A
In order to calculate a circle’s circumference, we need to know either its diameter or its radius. We then use the appropriate value in this equation: \(C=2πr\) (where “r” represents radius, of course). Here’s an example: Find the circumference of this circle: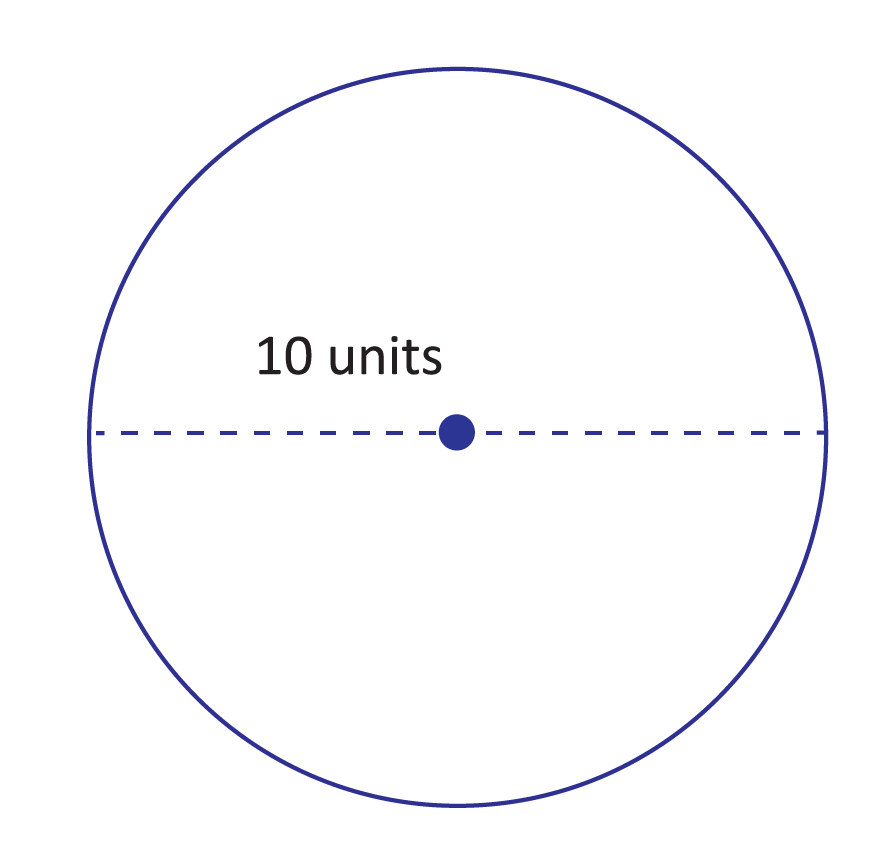 
\(r=\frac{10\text{ units}}{2}=5\text{ units}\)
Q
Why is circumference \(2πr\)?
A
We know that circumference is the length of the entire outer edge of a circle. (We could think of it this way: circumference is to circles what perimeter is to triangles, rectangles, pentagons, and so on!) With this in mind, let’s rearrange the variables in the equation \(C=2πr\) to get \(C=2r\timesπ\). Remember that \(2r=d\) (where d represents diameter), so we could rewrite this equation yet again: \(C=d\timesπ\). In other words, we can wrap a string (which is the same length as the diameter) around the circle 3.1415926… times.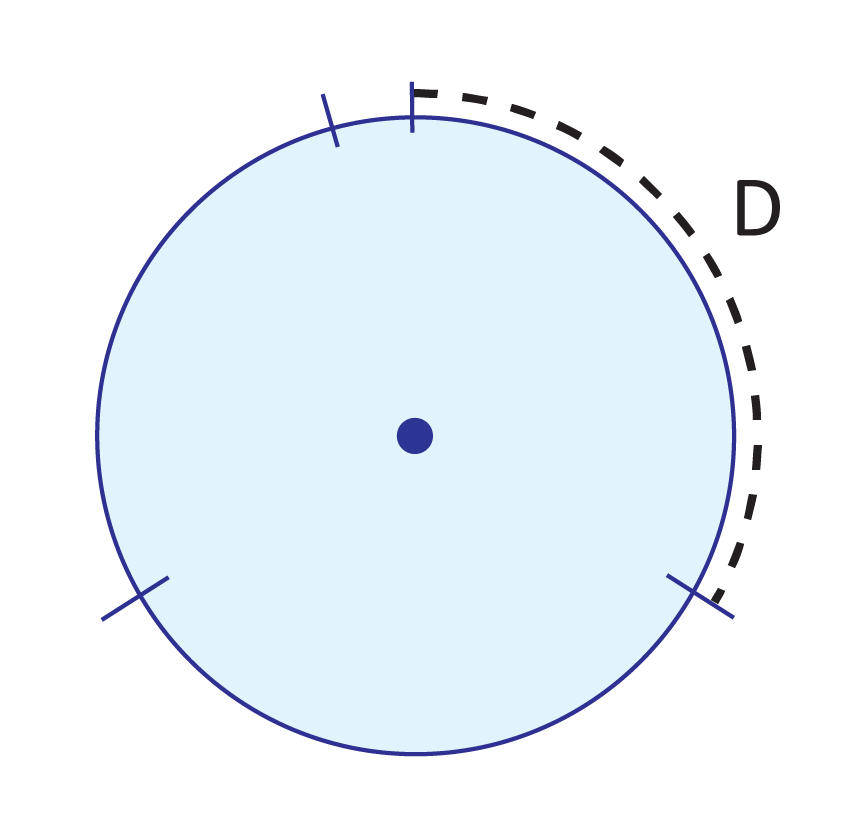
Q
How do we use circumference in everyday life?
A
The applications of circumference in everyday life are truly endless! One example, though, is determining how large of a tire someone needs for a bike or for a car. Another example would be finding how much wood is in a tree: with a very, very old tree, it would be pretty difficult to measure the diameter of the tree’s base; but it’d be straightforward to wrap a rope around the base and measure the circumference. Then, you could use this circumference measurement and ‘reverse-engineer’ the circumference equation to determine the tree’s diameter. With this measurement (and the height of the tree), we could find the volume of wood within this tree. Again, the list of examples could go on and on forever, so keep an eye out for other ways that you use circumference throughout your life!
Q
What is circumference vs diameter?
A
Circumference is the length of one complete ‘lap’ around a circle, and diameter is the length of the line segment that cuts a circle in half. Think of circumference as an outer measurement and diameter as an inner measurement of the circle!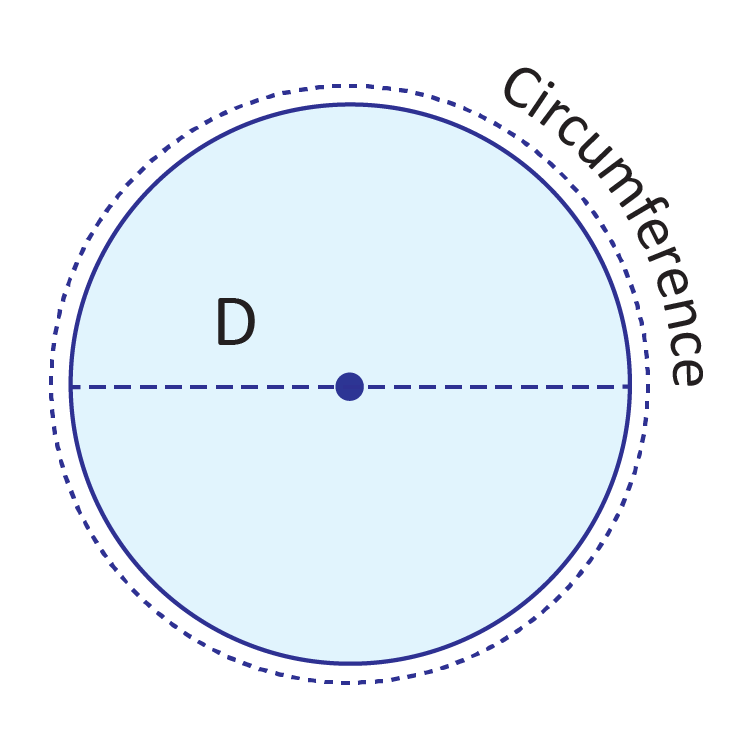
Q
Is diameter half the circumference?
A
No! Remember the equation \(C=2πr\) can be rewritten: \(C=2r\timesπ\), \(C=d\timesπ\), or \(C=πd\). So, perhaps we could say that diameter is 3.1415926…th of the circumference…
Q
Is a diameter a length?
A
If length is defined as the distance between two points, then yes, diameter is a length. The diameter of a circle measures the distance between the two furthest points on a circle.
Circle Practice Questions
Determine the circumference of the circle.
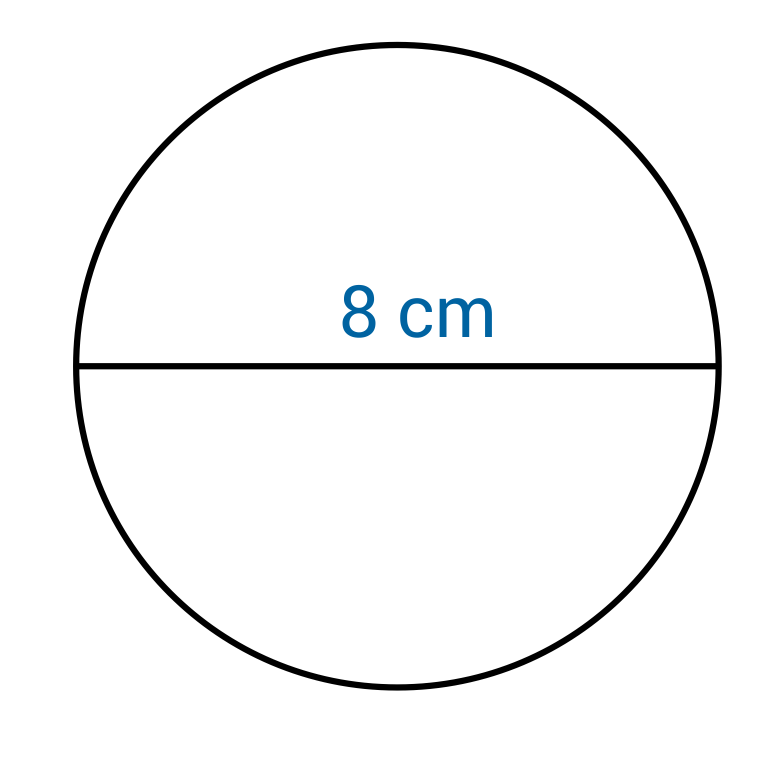
The circumference of a circle can be calculated using either \(C=𝜋d\) or \(C=2𝜋r\).
We know that the diameter of the circle is 8 cm, and an approximation for pi is 3.14, so we can plug these values into the formula \(C=𝜋d\). The formula becomes \(C=(3.14)(8)\), which simplifies to 25.12. The circumference of the circle is 25.12 cm.
Determine the radius of the circle if the circumference is twenty-three inches. Round your answer to the nearest hundredths.
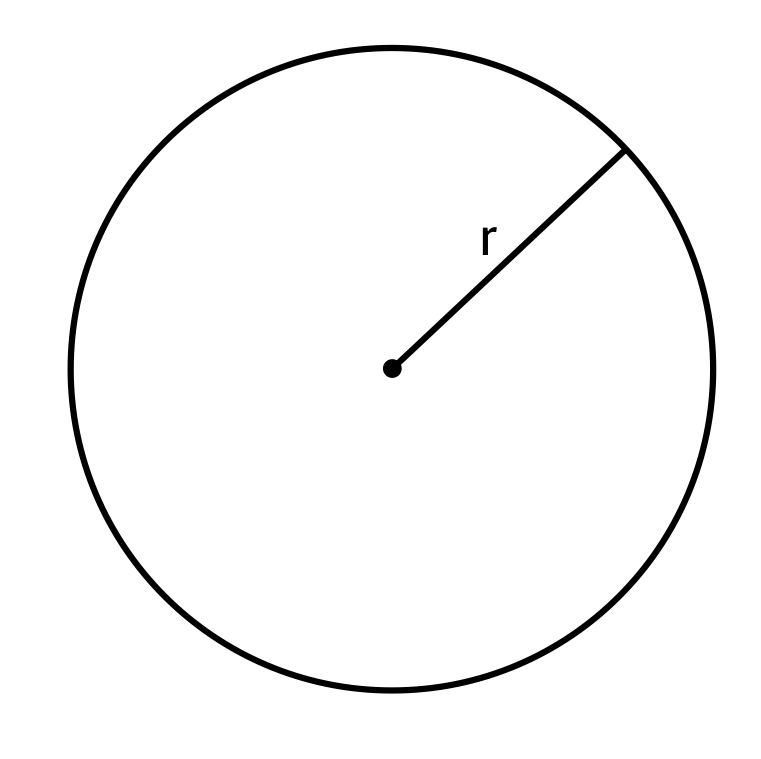
The radius of a circle can be calculated if the circumference is known. We know that the circumference of the circle is twenty-three inches, so we can plug this into the formula \(C=2𝜋r\). We also know that an approximation of pi is 3.14, so the only value we do not know is r, the radius. When C and 𝜋 are plugged into the formula it becomes \(23=2(3.14)r\). This can be simplified to \(23=6.28r\), and then both sides of the equation can be divided by 6.28 in order to isolate the variable r. 23 divided by 6.28 equals 3.66 when rounded to the nearest hundredth. The radius of the circle is 3.66 inches.
If C represents circumference, r represents radius, and d represents diameter, which formula is incorrect?
\(r=𝜋dC\) is incorrect because multiplying pi, times diameter, times circumference does not equal the radius. If the diameter is known, then the radius is simply half the value of d.
Bicycles from the 1800s look very different from the bikes we see today. In the photograph below, the bicycle’s back wheel has a radius of 9 inches, and the front wheel has a diameter of 60 inches. Using 3.14 as an approximation for pi, what is the difference between the circumference of the front and back wheel?
Before comparing the front and back wheel, we need to calculate the circumference of each wheel individually. The circumference of a circle can be found using the formula \(C=2𝜋r\) or \(C=𝜋d\). We know the radius of the back wheel is 9 inches, so we can plug this into the formula \(C=2𝜋r\). The formula becomes \(C=2𝜋(9)\) which simplifies to 56.52. The front tire has a diameter of 60 inches so we can plug this into the formula \(C=𝜋d\). The formula becomes \(C=𝜋(60)\) which simplifies 188.4. Now that we know the circumference of each wheel we can simply subtract 56.52 from 188.4. The difference in the wheel circumferences is 131.88 inches.
Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? Use 3.14 as an approximation for pi.
The formula \(C=2𝜋r\) can be used to calculate the circumference of the ferris wheel. We can plug in 68 for the radius, and 3.14 as an approximation for pi. The formula \(C=2𝜋r\) becomes \(C=2(3.14)(68)\) which simplifies to 427.04, or approximately 427 meters.