
Hi, and welcome to this review of parallelograms. Today we’re going to learn how to find the area and perimeter of a parallelogram.
Let’s get started!
Parallelogram Definition
Let’s define a parallelogram as a quadrilateral where both pairs of opposite sides are parallel and congruent. Congruent means the same length.
Now let’s look at a quick example problem.
Finding the Area and Perimeter of a Parallelogram
Find the area and perimeter of this figure:
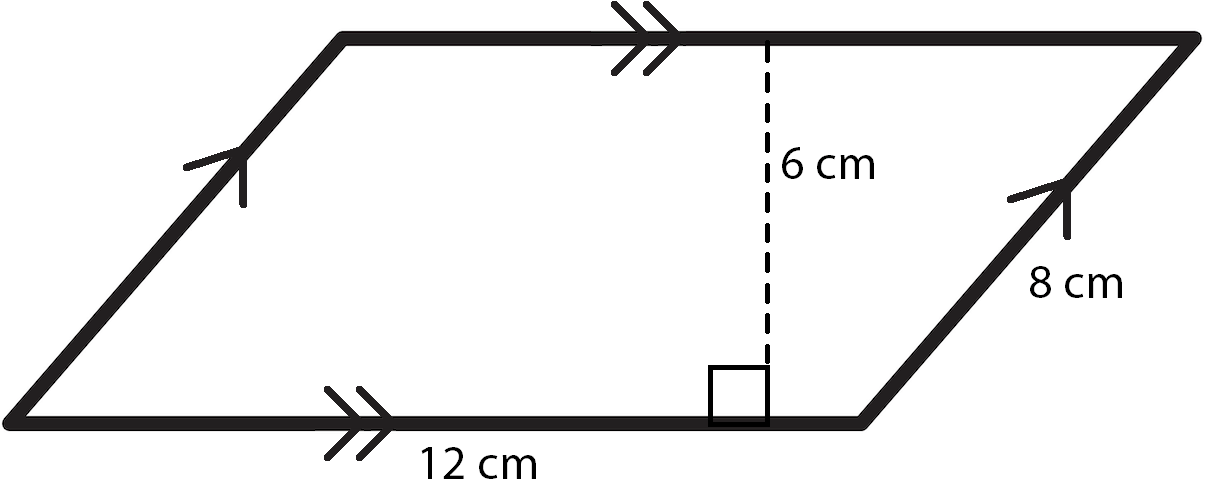
The first thing we need to do is determine if this shape is a parallelogram or not. It has four sides, so we know it’s a quadrilateral. And it has the same arrow marks on opposite sides, indicating that it has two sets of parallel sides. So it definitely is a parallelogram.
What else can we see? The bottom side has a measure of 12 cm, the side on the right has a measure of 8 cm, and the dashed line inside the parallelogram has a measure of 6 cm. But since this is a parallelogram we know that opposite sides are congruent. So we can label the other two sides as well. The top side has to be the same as the parallel bottom side and the left side has to be the same as its parallel right side.
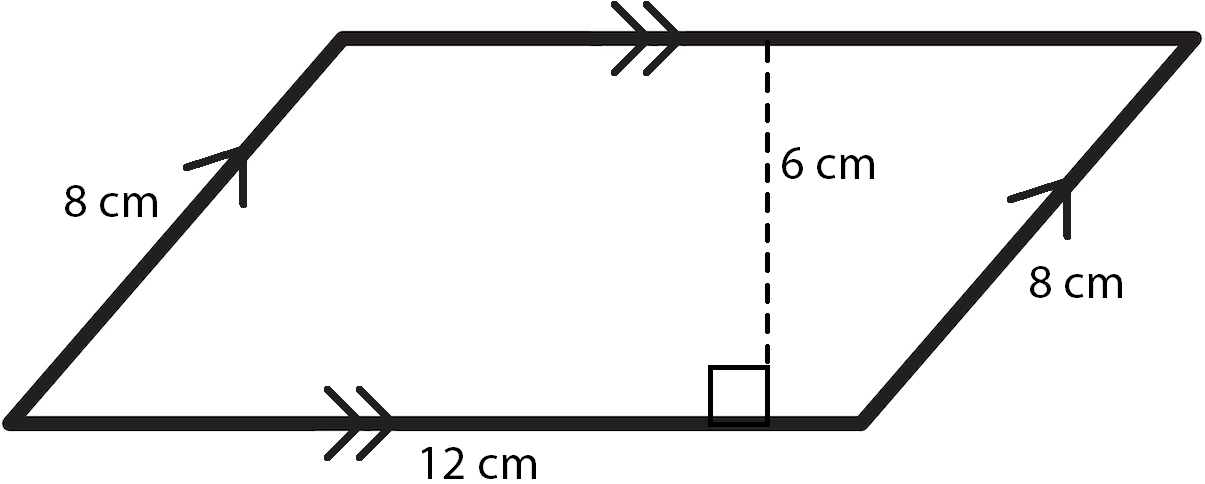
Finding the Perimeter
Now let’s find the perimeter. The perimeter is the distance around an object. So for any polygon, we can find the perimeter by simply adding all the sides together. Since we did the work of finding the measure of the top and left sides already, we just need to add \(8 + 12 + 8 + 12\) to get 40 cm. We don’t use the 6 cm measure at all for the perimeter, but we will need it to find the area.
Finding the Area
The formula for the area of a parallelogram is very simple: \(A = bh\), or \(\text{Area}=\text{base}\times \text{height}\). But which of the numbers in our problem is the base and which number is the height? The key is to look at the dashed line with the right angle symbol. This is the height, which is sometimes called the altitude. In our sample problem, it is 6 cm.
Once we find the height, we can find the base, because the height, or altitude, is perpendicular to the base. So, in this case, the height is perpendicular to the top and bottom sides of the parallelogram. It doesn’t matter whether we pick the top or the bottom to be the base because they are congruent. For our sample problem, the base is 12 cm. Now, all we have to do is plug these numbers into our formula: \(A=bh=(12)(6)=72\text{ cm}^{2}\)
We need to be sure that we have our units right. For area, the units are always squared, while for perimeter they are not. The area of our parallelogram is \(72\text{ cm}^{2}\), or 72 square centimeters.
Notice that we didn’t use the measure of the left or right sides to find the area of our parallelogram. That measure was necessary to find the perimeter but is not used at all in our formula for area.
Now, there is one thing we need to look out for. Sometimes a parallelogram has dimensions that make the height look a little bit strange:
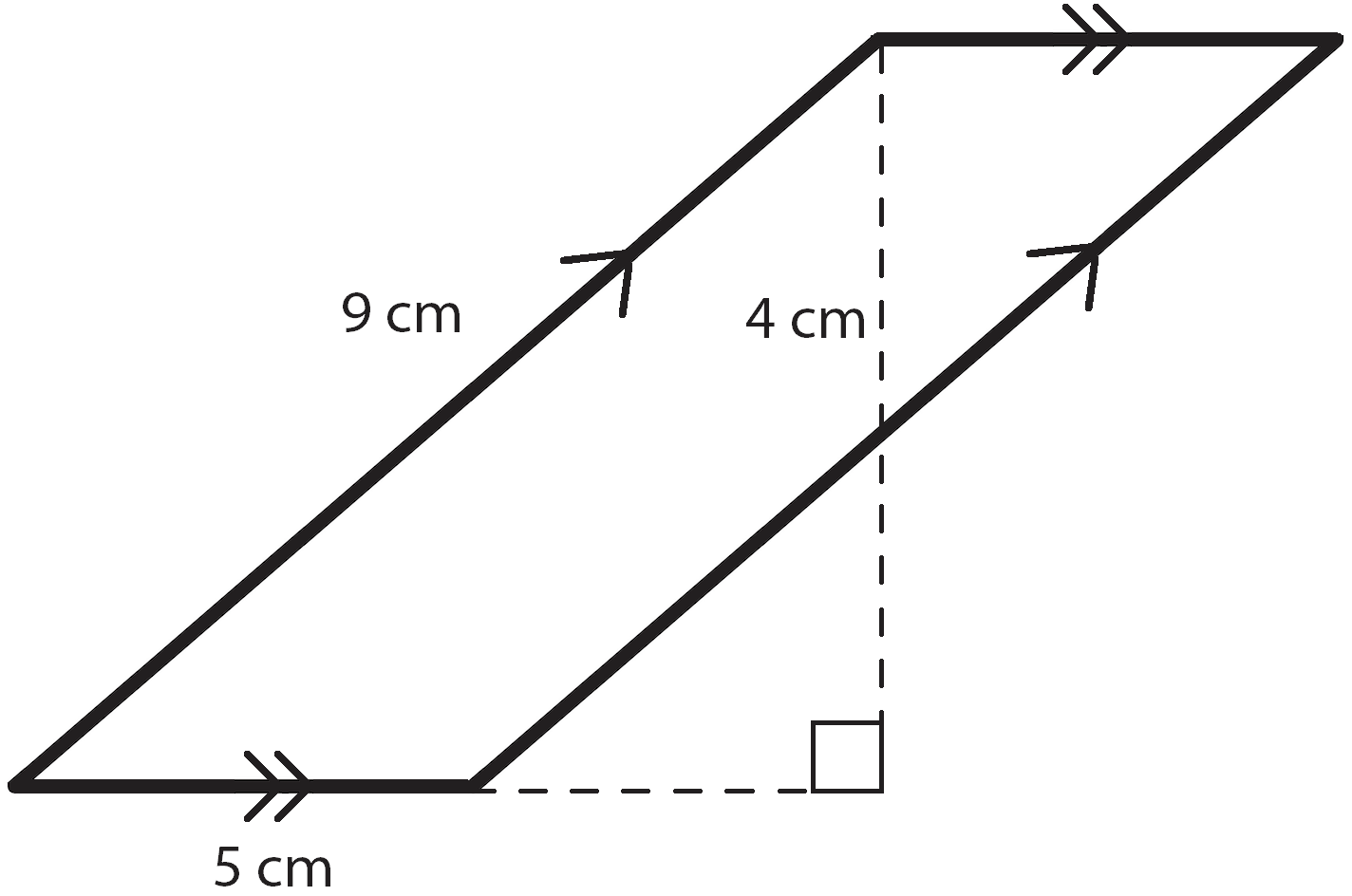
If we try to draw a dashed line from the bottom to the top to measure the height, the left side of our parallelogram gets in the way. So, we have to draw it with a dashed extension of the base. So the height here is 4 cm and the base is the bottom side and measures 5 cm. Using \(A = bh\) we are able to multiply \(5\cdot 4\) to get \(20\text{ cm}^{2}\). To find the perimeter, we can write in the measurements for the congruent opposite sides so the right side is 9 cm and the top side is 5 cm. Then we simply add together all four sides: \(P=9+5+9+5=28\text{ cm}\).
Thanks for watching and happy studying!
Area and Perimeter of a Parallelogram Practice Questions
Which of the following is not part of the definition of a parallelogram?
The correct answer is all angles are right angles. The definition of a parallelogram is, a quadrilateral where all opposite sides are parallel and of equal length, and all opposite angles are equal.
What is the area of this parallelogram?
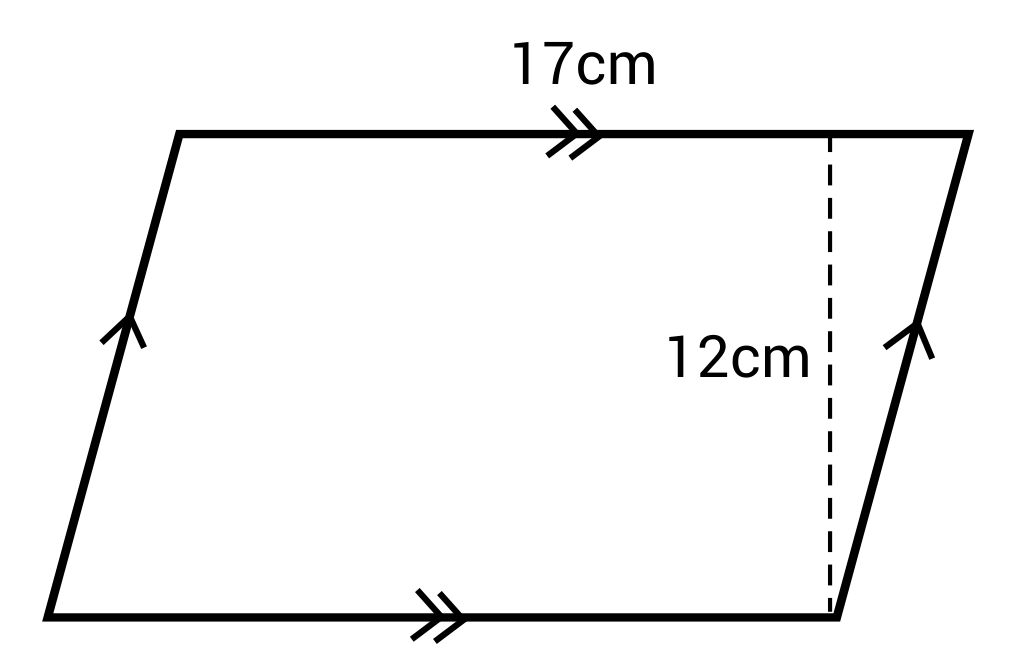
The correct answer is 204 cm2. The formula of a parallelogram is:
\(A=bh\)
The base (b) is 17 cm and the height (h) is 12 cm.
\(A=(170)(12)=204\text{ cm}^2\)
The area of this parallelogram is 204 cm2.
“A quadrilateral where all side lengths and angle measures are equal” is the definition of what shape?
The correct answer is a square. This is the exact definition of a square. It has all equal sides and all equal angles.
What is the area of a square with a side length of 4 in?
The correct answer is 16 in2. The formula for area of a square is:
\(A=s^2\)
The length of the side (s) is 4 in.
\(A=(4)^2=16\text{ in}^2\)
The area of this square is 16 square inches.
What is the area of this rectangle?
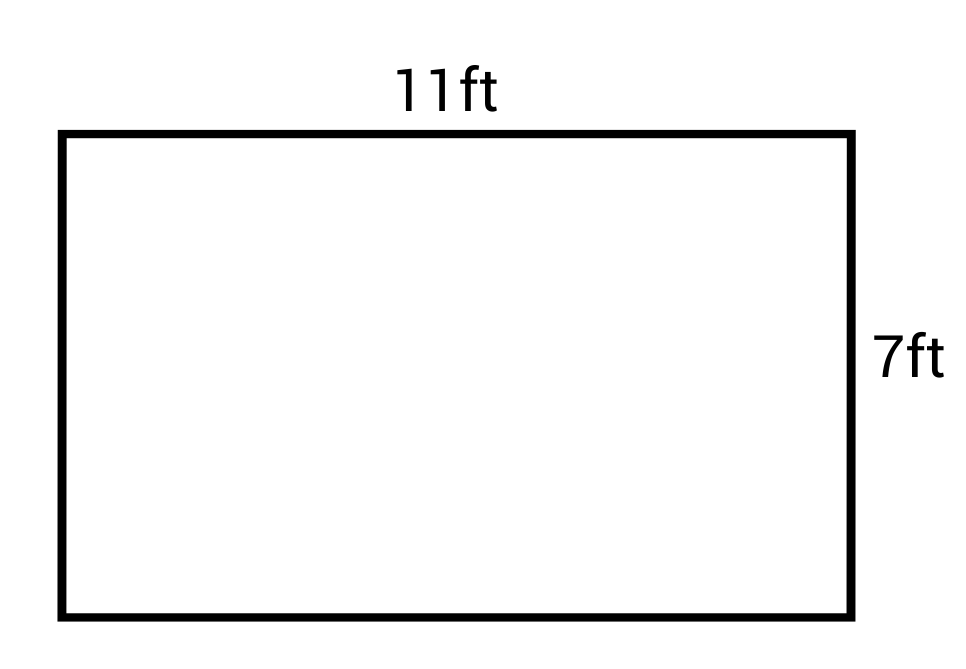
The correct answer is 77 ft2. The formula for area of a rectangle is:
\(A=lw\)
The length (l) is 17 ft and the width (w) is 7 ft.
\(A=(11)(7)=77\text{ ft}^2\)
The area of this rectangle is 77 square inches.