
Hello! Today we’re going to discuss two important words in geometry: similar and congruent.
Understanding the meaning of these two words is often the key to answering geometry test problems, so let’s get started.
Congruent vs. Similar
Congruent means “equal in size and shape.” So for two triangles to be congruent, they must have the same length sides and the same angles between those sides. Basically, the triangles must be perfect clones of each other.
Similar triangles are the exact same shape but don’t have to be the same size. So for a triangle to be similar, the angles in both triangles will all be the same and the sides will be in proportion for all sides. That means that if one side of a triangle is only half as long as the corresponding side in the other triangle, the other two sides must also be half as long as the corresponding sides in the bigger triangle.
The definitions of congruent and similar are true for any polygon. Any two polygons that are exactly the same size and shape are congruent, and any two polygons that are the exact same shape but not necessarily the same size are similar.
Complex Similar Shapes
We see complex similar shapes in models. A model house has the same shape as the real life house it’s representing, but it’s been scaled down. Suppose a model of a house is 1/36 the size of the real house. All the angles are the same, but every side is thirty-six times longer on the real house.
One thing to keep in mind is that if two polygons are congruent, then they are also similar. That’s because by definition, congruent polygons are the same shape, which is the sole requirement for polygons being similar. But not all similar polygons are congruent, since they can be different sizes, which disqualifies them from being congruent.
Determining Similarity
So, how do we determine if two polygons are similar? If all the corresponding angles of two polygons are the same measure and all the corresponding sides are in proportion, then the two polygons are similar. With problems involving polygons with four or more sides, we’re more likely to be given the information that the two polygons are similar so that we can use that information to find a missing side or angle.
Example Problem
Here’s a sample problem:
Find the missing angle and side of these similar quadrilaterals.
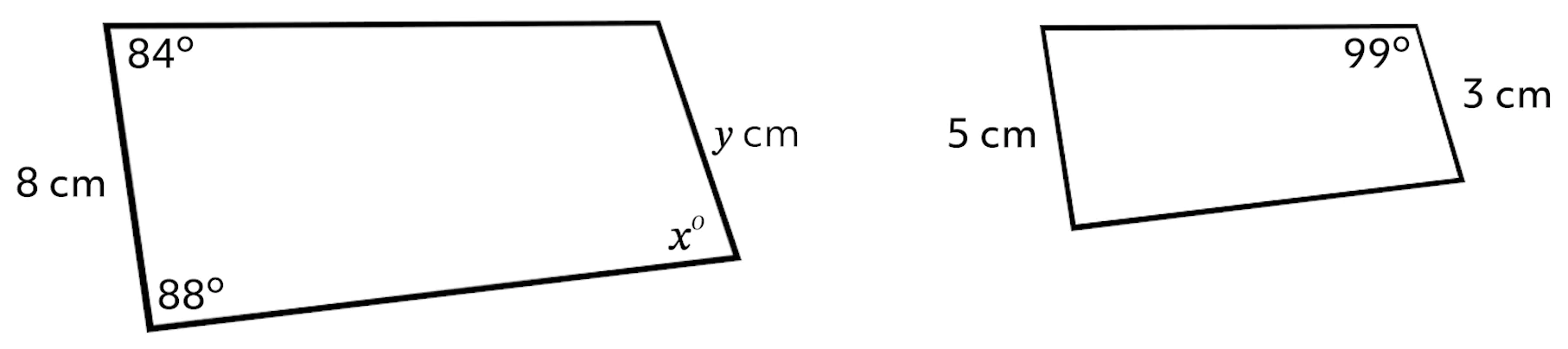
We can use our knowledge of similarity to find these missing measures. Since the quadrilaterals are similar, all their corresponding angles will be the same. So the top right angle of our larger quadrilateral must be 99 degrees just like it is in the smaller quadrilateral. And once we know that, we can find our missing angle \(x\) because the interior angles of a quadrilateral must add up to 360 degrees.
\(x=89^{\circ}\)
To find the missing side \(y\), we need to set up a proportion.
To solve this proportion, we need to cross multiply. Cross multiplying gives us \(5y=24\), and dividing both sides by 5 gives us \(y=4.8\). So, the missing side length is 4.8 cm.
Finding these two values was only possible because we know that similar figures have the same angles and proportional sides.
Similarity of Regular Polygons
Before we wrap up, let’s cover one more essential thing to know about similarity and congruence.
All regular polygons are similar to every other regular polygon with the same number of sides. So all regular pentagons are similar.
So are all regular hexagons and octagons and so on. That’s because by definition, all the interior angles of a regular polygon are the same measure. All the interior angles of a regular pentagon are 108°, all the angles of a regular hexagon are 120°, and all the angles of a regular octagon are 135°.
That’s it for similar and congruent polygons. I hope this video was helpful. Thanks for watching, and happy studying!
Congruent Shape Practice Questions
Which statement is true?
Congruent figures have the exact same size and shape. Even when reflected, rotated, or translated, their size and shape remain identical.
Identify the type of transformation shown in the two congruent shapes below:
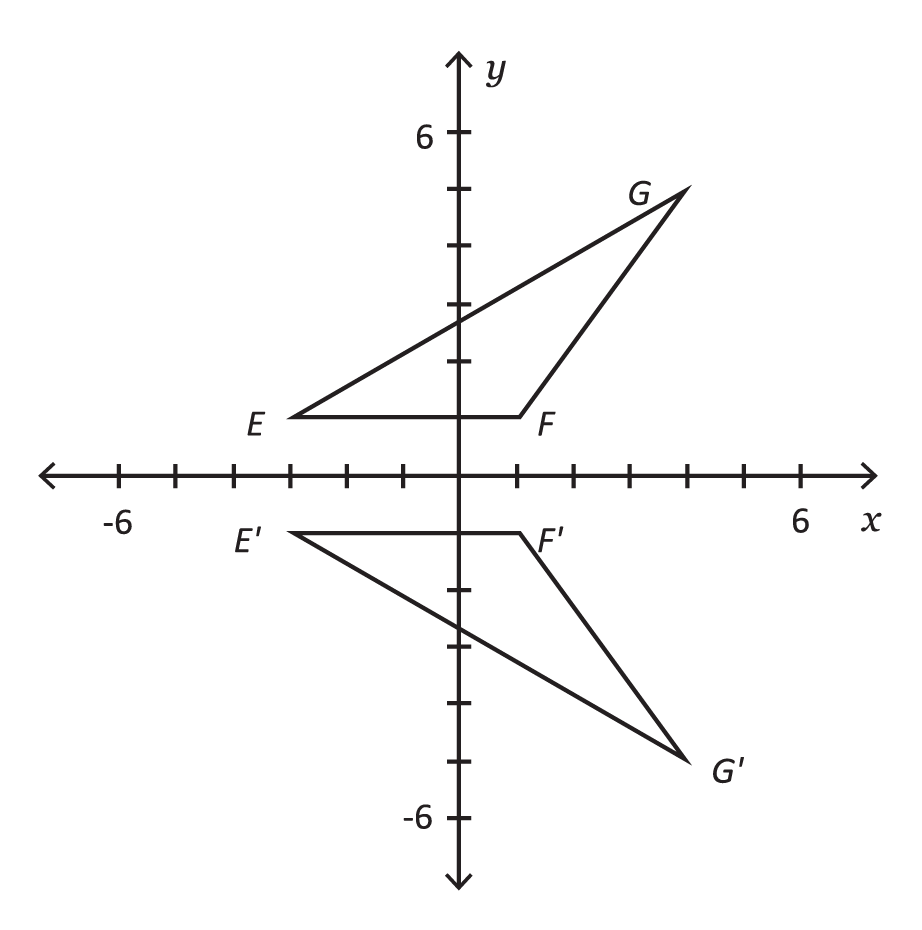
Triangle EFG is reflected across the x-axis so that one triangle shows a mirror image of the other. Therefore, this is an example of a reflection.
Which type of transformation moves a figure by sliding it vertically, horizontally, or both?
A translation happens when a congruent shape slides to another position without being rotated or flipped. The congruent shape can be translated vertically and horizontally.
Caleb works at an art museum and is in charge of a new sculpture installation. He proposes a location for the sculpture and presents it to his boss. Caleb’s boss wants the sculpture turned to the left, as shown in the image below. What type of transformation is this?
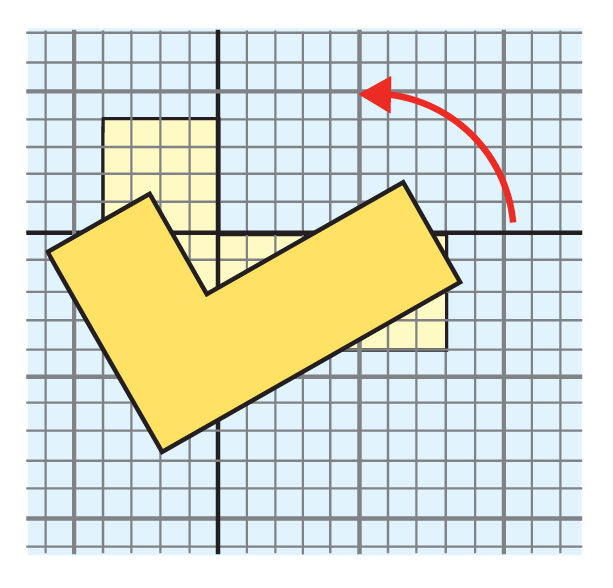
When a congruent shape is turned, it’s rotated about a fixed point. The L-shaped sculpture is turned counter-clockwise to a new position. Therefore, the transformation taking place is rotation.
Janelle used a ruler to trace a line on a piece of graph paper. Her line was five units long. Then, she slid her ruler down eight units and traced another line on the graph paper. This line was also five units long. What type of transformation did Janelle perform?
A translation happens when a figure is moved from one location to another by sliding it in a horizontal or vertical direction. The size and shape of the figure remain the same. Since Janelle slid her ruler eight units down and created a line identical to her original line, she performed a translation.



