
Hello! This video explains how to find the area and perimeter of rectangles and squares.
What are Area and Perimeter?
The word perimeter comes from a Greek prefix peri– that means “around” and a Greek root metron that means “measure.” Thus, the perimeter of a figure is the measure, or distance, around it.
The word area is from Latin, meaning “open space.” Thus, the area of a figure is the size of the open “floor space” inside the figure.
So, if you are buying stone tiles to pave a patio, you want to know the area of the patio. But if you are buying fencing to go around a patio, you want to know its perimeter.
Perimeter of a Square
To find the perimeter of a square, add up the four sides. Since all four sides of a square are equal, we can also just multiply the length of one side by 4. This gives us a formula for the perimeter of a square.
If a square has sides of length \(s\), then the perimeter of the square is \(P=s+s+s+s\), or \(P=4s\).
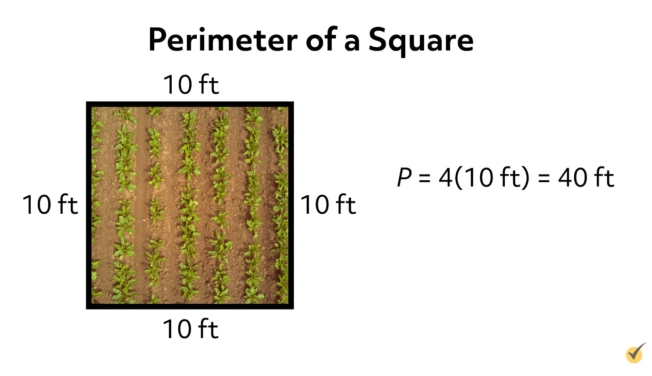
Example #1
For example, suppose you have a small square garden plot 10 feet on each side. Then its perimeter is 4 times the side length of 10 feet, namely 40 feet. So, you would need 40 feet of fencing to build a fence around the garden.
Note that perimeter is a distance, so we measure it in simple distance units like feet, inches, meters, or kilometers.
Example 2
Here is an example for you to try.
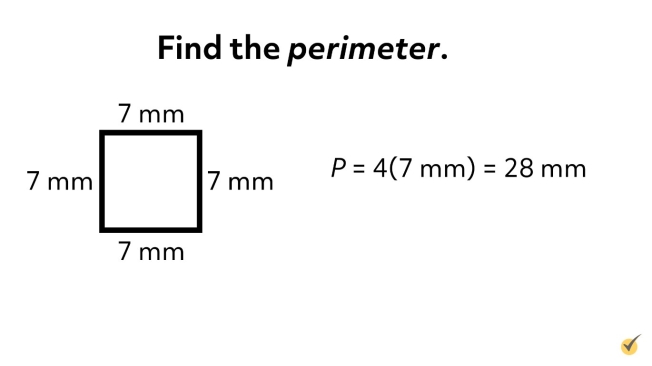
Suppose you have a small square that measures 7 mm on each side. What is its perimeter? Be careful to state the units of your answer. Pause the video now while you work out the solution, and then press play to compare your answer to mine.
The perimeter of the small square is 4 times the side length of 7 mm, which is 28 mm.
Perimeter of a Rectangle
To find the perimeter of a rectangle, you can just add up the four sides, just like you did with the square. But since opposite sides of a rectangle are equal, you can also add twice the length plus twice the width. This gives us the perimeter formula \(P=2l+2w\), where \(l\) is the length and \(w\) is the width of the rectangle.
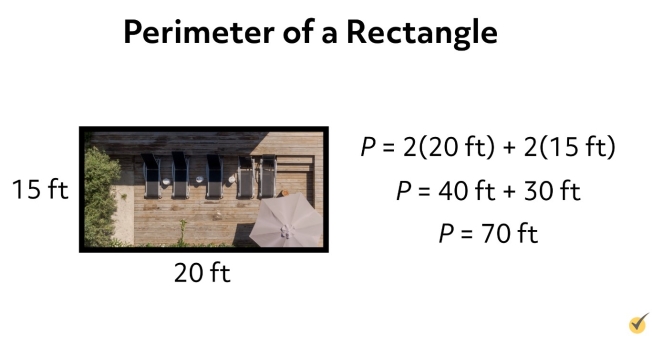
Example #1
For instance, suppose you have a rectangular patio that is 20 feet long by 15 feet wide. 2 times 20 feet is 40 feet, and 2 times 15 feet is 30 feet. So, we add 40 feet and 30 feet to get a perimeter of 70 feet.
 Example #2
Example #2
Now it’s your turn! Suppose you have a rectangular garden plot 45 feet long and 25 feet wide. What is its perimeter? Remember to state the units of your answer. Pause the video now while you work out your solution. Then press play to compare your answer to mine.

2 times the 45-foot length is 90 feet, and 2 times the 25-foot width is 50 feet. We add 90 feet and 50 feet, to get 140 feet for the perimeter of the garden plot.
Area of a Rectangle
Now let’s take a look at finding the areas of these shapes. Let’s start with the rectangle this time. To find the area of the rectangle, we multiply the length by the width. This gives us the area formula \(A=lw\), where \(l\) represents length and \(w\) represents width.
Example #1
Suppose we have a closet that has a rectangular floor that measures 4 feet long and 3 feet wide. We apply our formula to find that the area of the closet floor is \(A=(4\text{ }ft)(3\text{ }ft)=12\text{ }ft^{2}\). Because we multiplied two units of feet by each other, we square that unit in our answer. Area is always measured in square units.
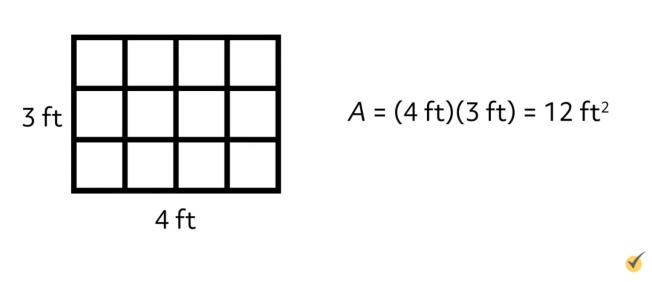
We can subdivide the rectangle every foot along the length and width to subdivide the rectangle into the 12 square feet that it takes to tile the floor.
Example #2
Here is another example for you to try on your own.
Suppose a rectangular parking lot is 15 meters long and 12 meters wide. What is the area of the parking lot? Be careful to state the units of your answer. Pause the video until you calculate your solution. Then, press play, and compare your answer to mine.
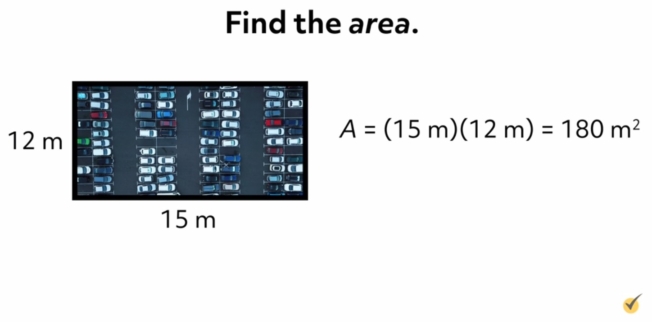
Since the length is 15 meters and the width is 12 meters, we apply our formula to find that the area is \(A=lw=(15\text{ }m)(12\text{ }m)=180 m^{2}\).
Area of a Square
Finally, we are going to talk about the area of a square.
We find its area by multiplying the length of a side by the width of a side. Since the width and length are equal in a square, we find the area by squaring the length of a side of the square.
By the way, this is the very reason that we call it “squaring” when we raise a number to the second power.
So, if a square has sides of length s, the formula for the area of the square is \(A=s^{2}\). In this diagram we shade the interior of the square to emphasize that we are measuring what is inside the square.
Example #2
For example, suppose we have a small closet whose floor is a square that measures 4 feet on each side. What is the area of the closet floor? Since the sides of the square are 4 feet long, the area of the square is \(A=(4\text{ }ft)^{2}=16\text{ }ft^{2}\).
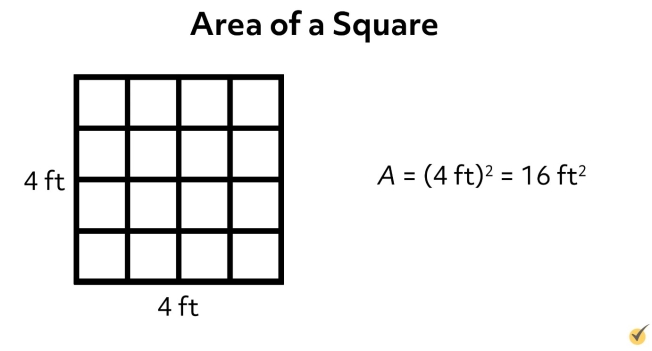
Note that if we subdivide the square every foot along each side, we subdivide the inside into 16 squares that are 1 foot on each side. We call each of these little squares a square foot, and it takes 16 of them to tile the floor of this closet. This is what we mean when we say that the area of the square is 16 square feet. Remember, we always measure area in square units like square feet, square inches, square meters, or square miles.
Example #2
Here is an example for you to try.
Suppose you have a square that measures 9 cm on each side. What is the area of the square? Be sure to include units in your answer. Pause the video while you work out your solution. Then continue when you are ready to compare your answer to mine.
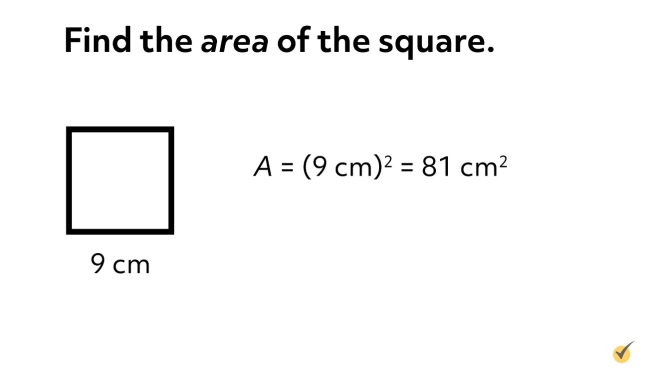
By our formula, the area of the square is \(A=(9 cm)^{2}=81\text{ }cm^{2}\). Did you remember to say “square centimeters” and not just “centimeters” in your answer? Some teachers and tests will count your answer wrong if you use the wrong units, so be very careful when you’re writing out your units!
Review
In this lesson, we learned how to find the perimeter and area of squares and rectangles. The perimeter of a figure is the distance around it, measured in simple distance units like feet or meters. The perimeter of a square is four times the side length, and the perimeter of a rectangle is twice the length plus twice the width.
Rectangle: \(P=2l+2w\)
The area of a figure is the size of the floor space inside it, measured in square units like square feet or square meters. The area of a square is the square of the side length, and the area of a rectangle is the length times the width.
Rectangle: \(A=lw\)
We can sum all of this up into four formulas that arise frequently in mathematics and are well worth memorizing. Remember, a square is a special type of rectangle, so if you are only able to remember your formulas for the area and perimeter of a rectangle, you can use those to find the area and perimeter of a square.
I hope that this video was helpful. Thanks for watching, and happy studying!