
Hi, and welcome to this video on finding the area of any triangle!
In this video, we will cover four different formulas:
- Area given base and height
- Area given all three side lengths
- Area of an isosceles triangle
- Area of an equilateral triangle
Basic Area of a Triangle Formula
We are going to start with the most common formula for area of a triangle.
This is the formula that you will use almost every time and the one that is usually taught in schools: \(A=\frac{1}{2}bh\), where \(b\) stands for the length of the triangle’s base and \(h\) stands for the triangle’s height.
This formula is useful for almost every triangle, especially if you are given the base and the height or can easily find them.
Let’s try a couple of examples.
Example #1
Find the area of the following triangle.
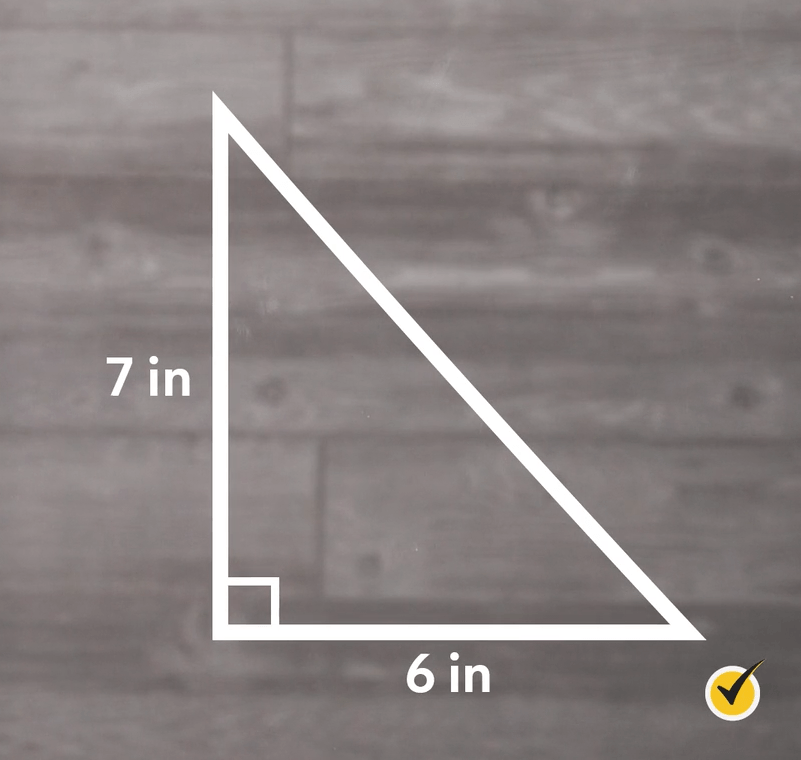
In this example, our base is 6 inches and our height is 7 inches. If we plug these values into our formula, we get:
Our area is 21 inches squared.
Example #2
Let’s try another one.
What is the area of this triangle?
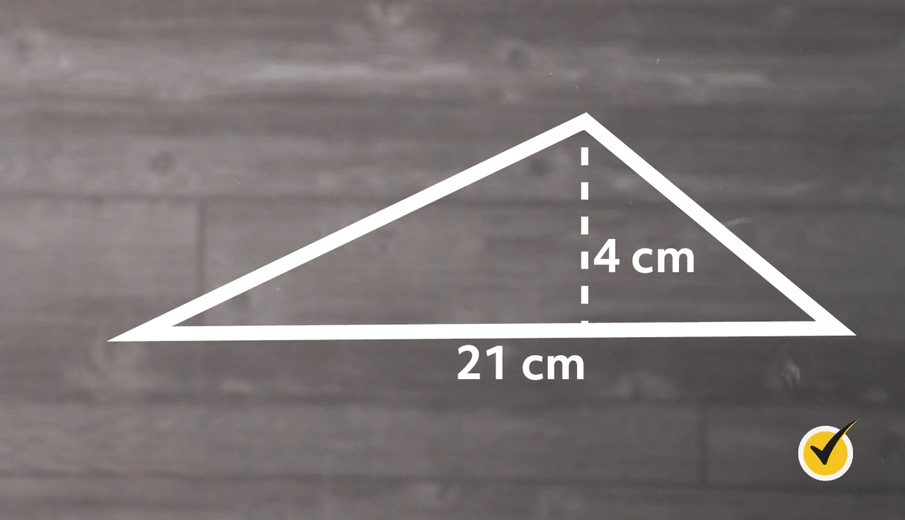
In this example, our base is 21 cm and our height is 4 cm. If we plug these numbers into our formula, we get:
We always write our formula, just so it helps us remember it.
The area of our triangle is 42 square centimeters.
Area of a Triangle Given Lengths of All Three Sides
The second formula we are going to cover is not as well known but is still extremely useful. It is the formula for finding the area of a triangle when you are given the lengths of all three sides. Depending on the triangle, there may be times when you can use the side lengths to find the height of the triangle, but this is not always possible, which is when the following formula comes in handy.
\(A=\sqrt{s(s-a)(s-b)(s-c)}\), where \(s\) is the semi-perimeter of the triangle and \(a\), \(b\), and \(c\) are each of the side lengths.
Let’s talk about semi-perimeter for a minute. Semi-perimeter isn’t something we come across often, so we need to break apart the word to figure out what exactly it means. We know that perimeter is the distance around an object, so it is the lengths of all the sides added together, but what does “semi” mean?
You may think of a semi-circle to help you understand. A semi-circle is half a circle, so in math, “semi” must mean half. Now that we know what each part of the word means separately, let’s put it together. Semi-perimeter must mean half of the perimeter.
Let’s try a couple of examples using this formula.
Example #1
What is the area of this triangle?
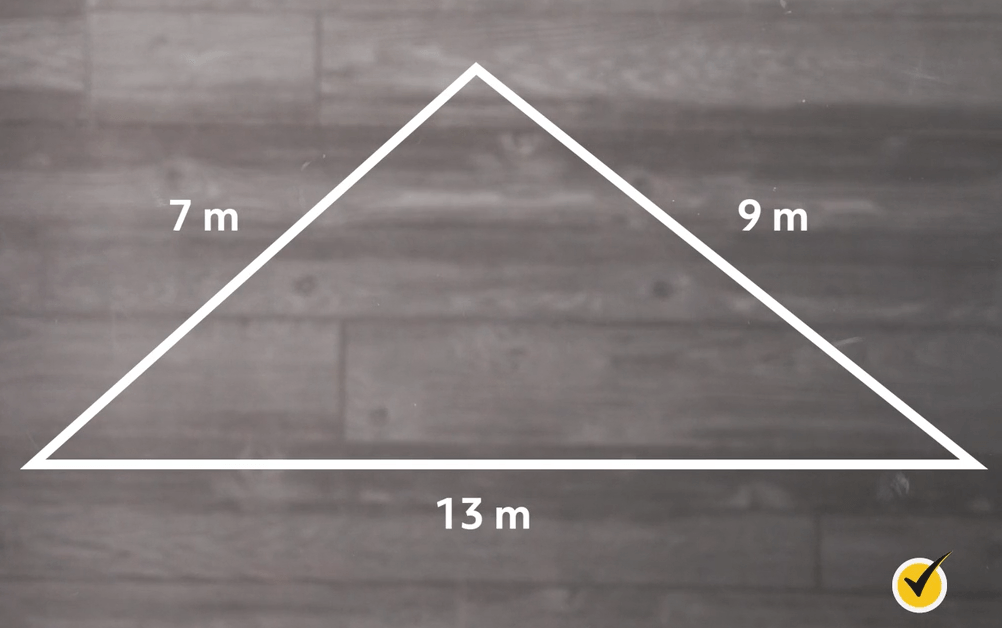
The first thing we want to do is write out our formula. I always recommend doing this because it helps you remember where to plug something in, and writing the formula out repeatedly will help you remember it.
We know our \(a\), \(b\), and \(c\) values, but we don’t know the value of \(s\), so before we can plug things into our formula, we need to figure out what \(s\) is. \(S\) stands for semi-perimeter, so we want to find the perimeter of our triangle and then divide by 2.
Now that we know that \(s\) is 14.5, we can plug all our known values into our equation.
\(=\sqrt{14.5(7.5)(5.5)(1.5)}\)
Which, when you simplify this out, is approximately equal to 29.95 square meters.
Example #2
Let’s try another one.
Find the area of the following triangle.
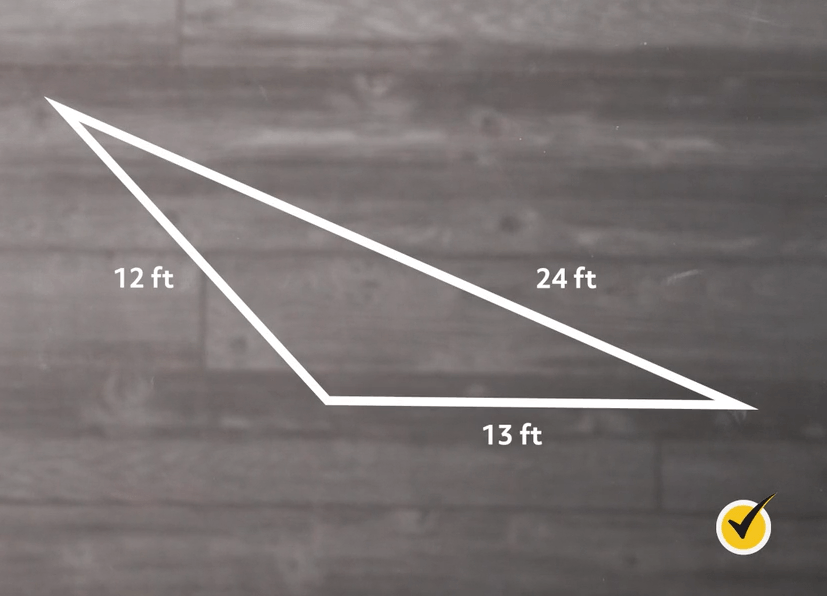
The first thing we need to do is write out our equation.
Now we need to find our semi-perimeter.
Finally, we plug all our values into the equation.
Which, when you simplify it out, is approximately equal to 41.96 square feet.
Area of an Isosceles Triangle
The next formula we are going to look at is a formula for finding the area of an isosceles triangle. The formula is \(A=\frac{1}{2}b\sqrt{a^{2}-\frac{b^{2}}{4}}\), where a is the length of one of the two congruent sides and \(b\) is the length of the unique side.
Let’s try out this formula on a couple of examples.
Example #1
What is the area of this triangle?
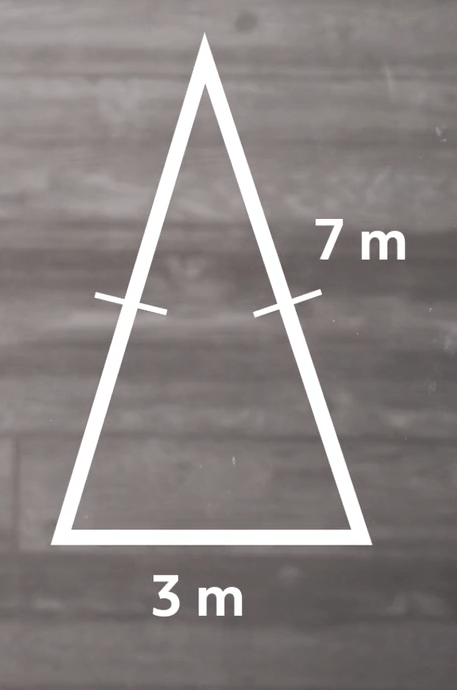
First, we’ll write out our formula.
Then we want to plug in our known values and solve.
\(=\frac{1}{2}(3)\sqrt{49-\frac{9}{4}}\)
\(=\frac{3}{2}\sqrt{\frac{196}{4}-\frac{9}{4}}\)
The 196 over 4 comes from converting our 49 to a fraction. So we did this by multiplying by 4 over 4 so that we have fractions with common denominators and are able to subtract them.
\(\approx 10.26\text{ m}^{2}\)
The area of our triangle is approximately 10.26 square meters.
Example #2
Try finding the area of this triangle:
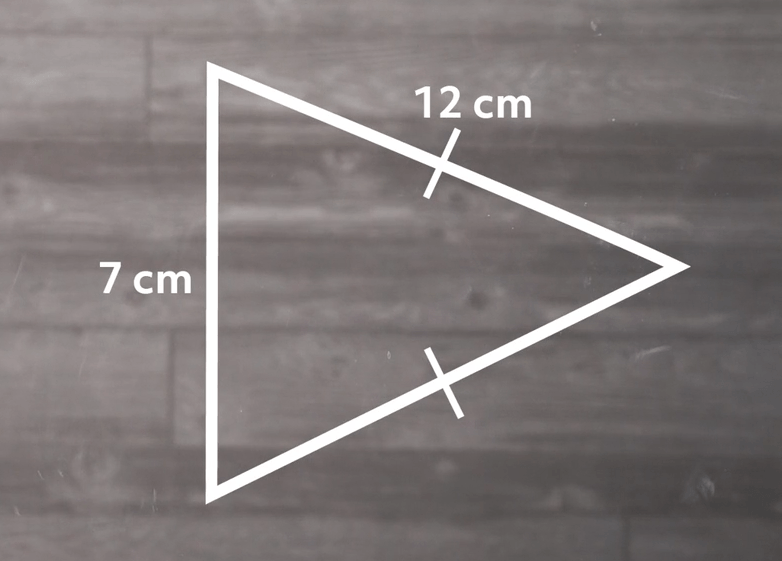
To find the area of our triangle, we are going to first write out our formula and then plug in our values to solve it.
\(=\frac{1}{2}(7)\sqrt{(12)^{2}-\frac{(7)^{2}}{4}}\)
\(=\frac{7}{2}\sqrt{144-\frac{49}{4}}\)
\(=\frac{7}{2}\sqrt{\frac{576}{4}-\frac{49}{4}}\)
\(=\frac{7}{2}\sqrt{\frac{527}{4}}\)
\(\approx 40.17\text{ cm}^{2}\)
The area of our triangle is approximately 40.17 centimeters squared.
Area of an Equilateral Triangle
The last formula we are going to look at is the formula for an equilateral triangle. This formula is \(A=\frac{\sqrt{3}}{4}a^{2}\), where \(a\) is the length of one of the sides.
Let’s look at a couple of examples.
Example #1
What is the area of an equilateral triangle with a side length of 2 ft?
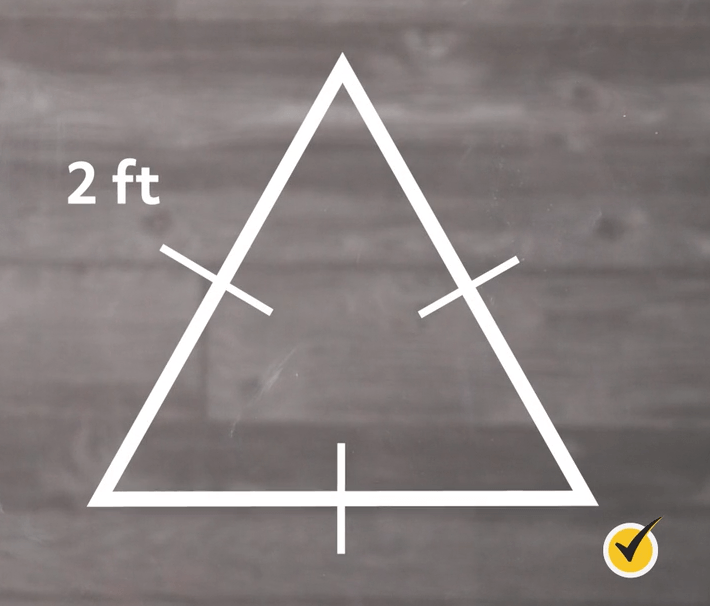
First, we’re going to write out our formula.
Now we are going to plug in our value for \(a\).
So the area of our triangle is the square root of 3 feet squared.
Example #2
Let’s try one more example involving an equilateral triangle.
What is this triangle’s area?
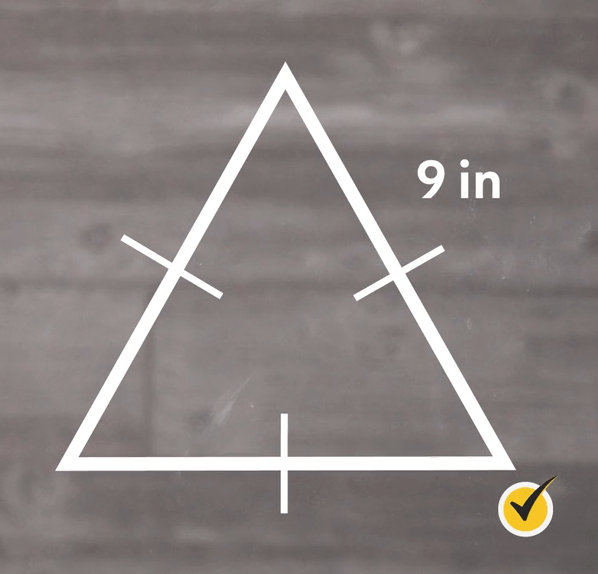
We find the area by writing out our formula and then substituting in our \(a\) value.
\(=\frac{\sqrt{3}}{4}(9)^{2}\)
\(=\frac{\sqrt{3}}{4}(81)\)
Which, when you simplify it, is approximately 35.07 square inches.
The area of our triangle is approximately 35.07 inches squared.
Review
We covered a lot of formulas in this video, but I hope they were helpful. Each of these formulas is useful, but the two most common ones are the first two we covered. If you don’t already have those two memorized, I would recommend doing that because they will come up frequently in your math classes.
Before we go, let’s look at a review question.
If you are given the triangle shown below, which area formula should you use?

- \(A=\frac{1}{2}bh\)
- \(A=\sqrt{s(s-a)(s-b)(s-c)}\)
- \(A=\frac{1}{2}b\sqrt{a^{2}-\frac{b^{2}}{4}}\)
- \(A=\frac{\sqrt{3}}{4}a^{2}\)
I hope this video was helpful. Thanks for watching, and happy studying!
