Hi, and welcome to this review of the Pythagorean theorem! We’re going to go over how to use it properly and also go over some special triangles called “Pythagorean triples” that could save you some time when taking tests. So, let’s get started!
Pythagorean Theorem Formula
First thing’s first: what is the Pythagorean theorem? The Pythagorean theorem is \(a^2+b^2=c^2\).
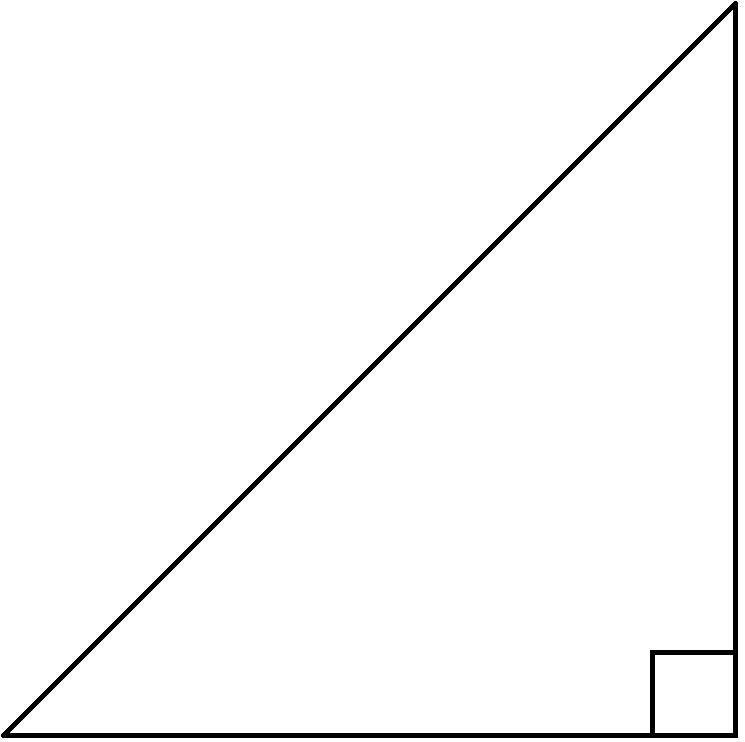
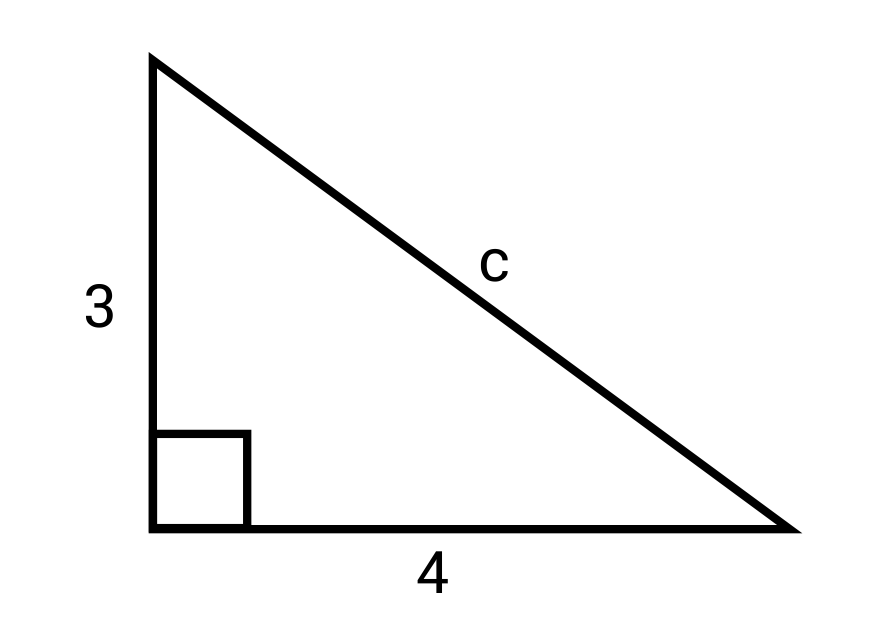
Now, this is used to find the length of a side of a right triangle when we know the length of the other two sides. The triangle has to be a right triangle, which means that it has an angle that measures exactly 90 degrees, like this one:
The theorem is very easy to remember and just as easy to use! In the theorem, \(a\), \(b\), and \(c\) are the lengths of the three sides of the triangle. But which is which? Let’s start by figuring out where to find \(a\), \(b\), and \(c\) in a triangle.
Applying the Pythagorean Theorem to a Triangle
To start, you can tell that you’re dealing with a right triangle because you can see this little square in one of the angles. That’s the symbol for a right angle (or 90˚ angle). Any triangle that has a right angle must be a right triangle.
So now we have to decide where to put the three side lengths. The key is to start with \(c\), which is always on the side across from the right angle.
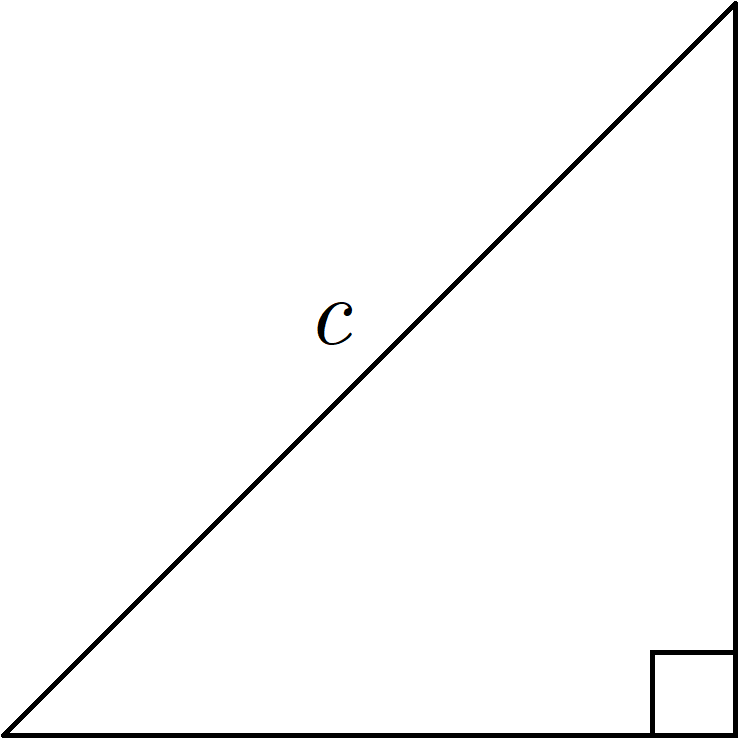
This is called the hypotenuse, and it’s always the longest side.
You may be asking yourself “If \(c\) is always across from the right angle, how do I tell which of the other two is \(a\) and which is \(b\)?” It’s a good question, and the answer is, it doesn’t matter! Either of these two sides, which are called legs, can be used as \(a\) and then just use the other one for \(b\). Let’s pick 3 cm for \(a\) and use 4 cm for \(b\). So this is what our theorem looks like when we have it filled in: \(3^2+4^2=c^2\)
Now we just can evaluate 3 squared and 4 squared, which means multiplying 3 times 3 and 4 times 4 to get the following:
\(9+16=c^2\)
So, what is the final answer for \(c^2\)? A little addition tells us.
\(25=c^2\) or \(c^2=25\)
Now here’s where it gets a little tricky. We now know that \(c^2=25\), but we want to know what \(c\) is, not what \(c\) squared is! So how can we get rid of that little 2? Well, we use the inverse, or opposite, operation of squaring something! And that inverse operation is the square root! Since it’s an equation, whatever we do to one side of the equation we must do to the other, so I’m going to take the square root of both sides.
The square root of \(c^2\) is \(c\) and the square root of 25 just happens to be 5. Look at that. It’s always good to check our answer to see if it makes sense.
Triangle Inequality Theorem
Since we’re finding \(c\), it should be longer than any of the other two sides, and 5 is greater than both 4 or 3. Also, because of the triangle inequality theorem, which is something we’ll get to in a later video, the hypotenuse must be less than the sum of the other two sides, which means 5 has to be smaller than 3+4. Which, it is.
Pythagorean Triples
So you might have noticed that the answer to this problem was a nice neat integer (5). This is actually kind of rare if we look at random triangles. But it’s not rare in a math problem you might see on a test. It happens whenever a problem uses a Pythagorean triple. The triangle we just looked at is the most common kind, of a 3-4-5 right triangle. The legs measure 3 and 4 and the hypotenuse is 5.
Sometimes it will be disguised by multiplying all the numbers by 2, which means we would get a (6-8-10) or multiplied by 10 which means we’d have a (30-40-50) lengths or any other number. You don’t need to know this to solve a Pythagorean theorem problem, but it’s a nice shortcut to save you some time or allow you to check your answer another way. Other Pythagorean triples include 5-12-13, 8-15-17, and 7-24-25. There are many more, but these ones are the ones you’ll see most often.
Final Example
Of course, there are right triangles that aren’t Pythagorean triples. Let’s look at one just so we can see what the answer will look like.
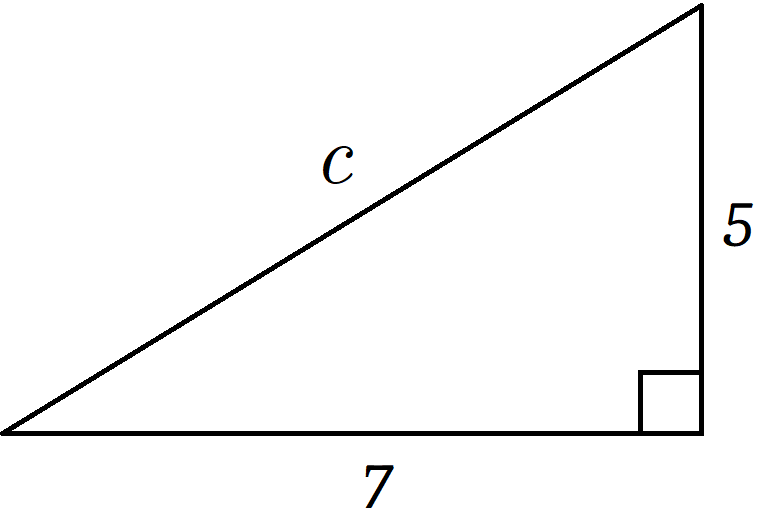
Once again we’re solving for the hypotenuse (the longest side, which is opposite the 90˚ or right angle.) This is length \(c\). When we plug in 5 and 7 for \(a\) and \(b\) we get this:
\(2^5+4^9=c^2\)
So let’s add 25 + 49 to get \(74=c^2\).
Then we take the square root of each side and find out that \(c = \sqrt{74}\), now even though 74 isn’t a perfect square. This is the answer. If you take the square root on a calculator you only get an approximation of the answer (which about 8.60232526…). We can use this approximation to do our checks: It’s greater than either of the other two sides and it’s less than the two sides added together. But when writing the answer we should use the square root form.
Thanks for watching, and happy studying!
Pythagorean Theorem Practice Problems
Solve for the value of C in the right triangle below:
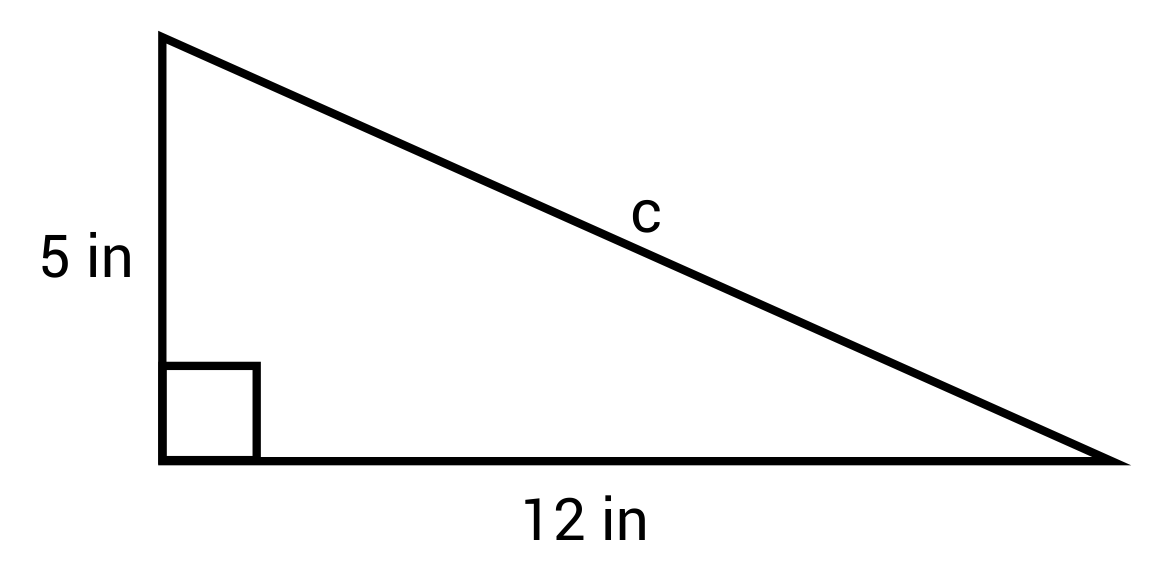
The correct answer is 13 inches. The Pythagorean Theorem states that \(a^2+b^2=c^2\), where a and b are the legs of the right triangle, and c is the hypotenuse. When the values for a and b are plugged into the equation, we have \(5^2+12^2=c^2\), which simplifies to \(25+144=c^2\). This then simplifies to \(169=c^2\). From here, find the square root of both sides of the equation. The square root of 169 is 13, and the square root of \(c^2\) is c. Therefore, \(c=13\) inches.
Solve for the value of C in the right triangle below:
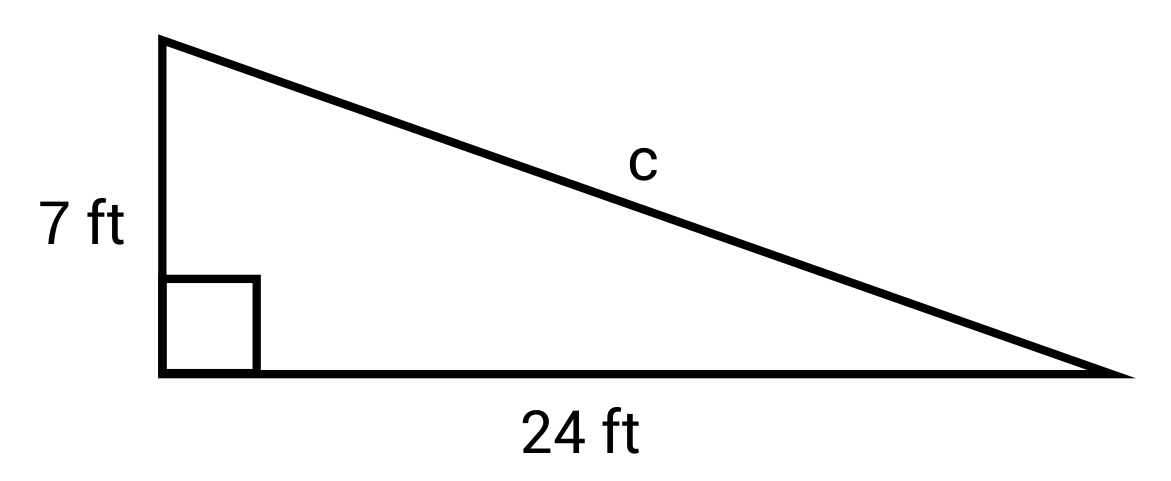
The correct answer is 25 ft. The Pythagorean Theorem states that \(a^2+b^2=c^2\), where a and b are the legs of the right triangle, and c is the hypotenuse. When the values for a and b are plugged into the equation, we have \(7^2+24^2=c^2\), which simplifies to \(49+576=c^2\). This then simplifies to \(625=c^2\). From here, find the square root of both sides of the equation. The square root of 625 is 25, and the square root of \(c^2\) is c. Therefore, \(c=25\) feet.
Solve for the value of C in the right triangle below:
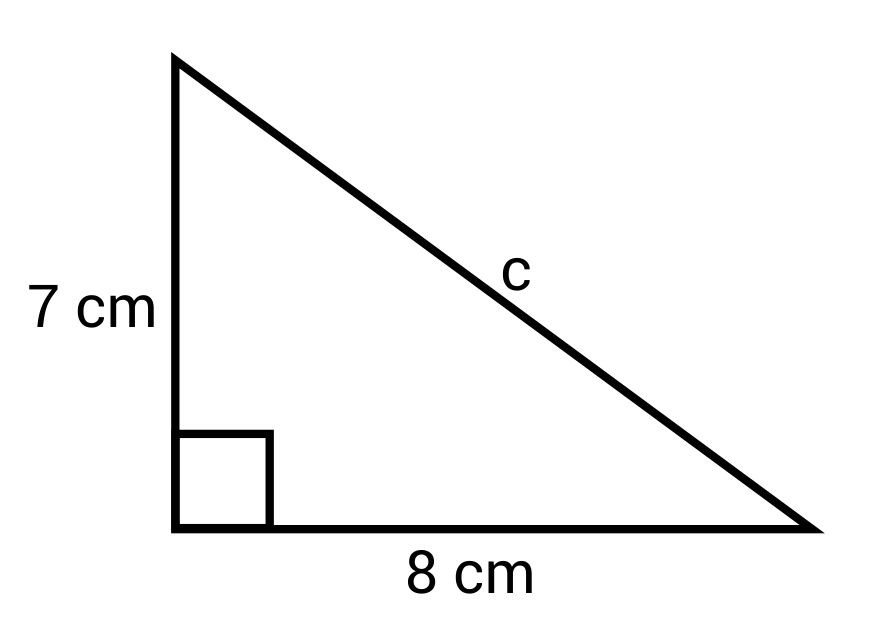
The correct answer is \(\sqrt{113}\) cm. The Pythagorean Theorem states that \(a^2+b^2=c^2\), where a and b are the legs of the right triangle, and c is the hypotenuse. When the values for a and b are plugged into the equation, we have \(7^2+8^2=c^2\), which simplifies to \(49+64=c^2\). This then simplifies to \(113=c^2\). From here, find the square root of both sides of the equation. The square root of \(c^2\) is c, but the square root of 113 is not a nice whole number, so we can leave it as \(\sqrt{113}\). Therefore, \(c=\sqrt{113}\) cm.
Which statement about the right triangle below is incorrect:
The correct answer is the hypotenuse if 4. Choice A is correct because the Pythagorean Theorem can be applied to solve for c. Choice B is correct because the hypotenuse (c) will always be the longest side of a right triangle. Choice D is also correct because a and b are defined as the two legs of a right triangle that come together to form the 90-degree angle. Therefore, only Choice C is incorrect.
Which right triangle lengths show incorrect values for a, b, and c according to the Pythagorean Theorem?
The correct answer is \(a=8, b=9, c=10\). The Pythagorean Theorem can be used to prove that the lengths of answer choice C are incorrect. If 8 is plugged in for a, 9 is plugged in for b, and 10 is plugged in for c, the result is \(8^2+9^2=10^2\). Simplifying each side of the equation shows that the two sides are not equal. 145 does not equal 100. Therefore, triangle C is incorrect.