
Hi, and welcome to this review of hyperbolas!
Not only do hyperbolas have an interesting name, but they’re actually a close relative of the ellipse, even though they look a bit different.
Horizontal Hyperbola Equation
To see how they’re related, let’s look at the equation for a horizontal hyperbola:
It looks almost exactly the same as the ellipse equation, except that instead of addition between the two fractions, we see subtraction.
Now, let’s see what it looks like:
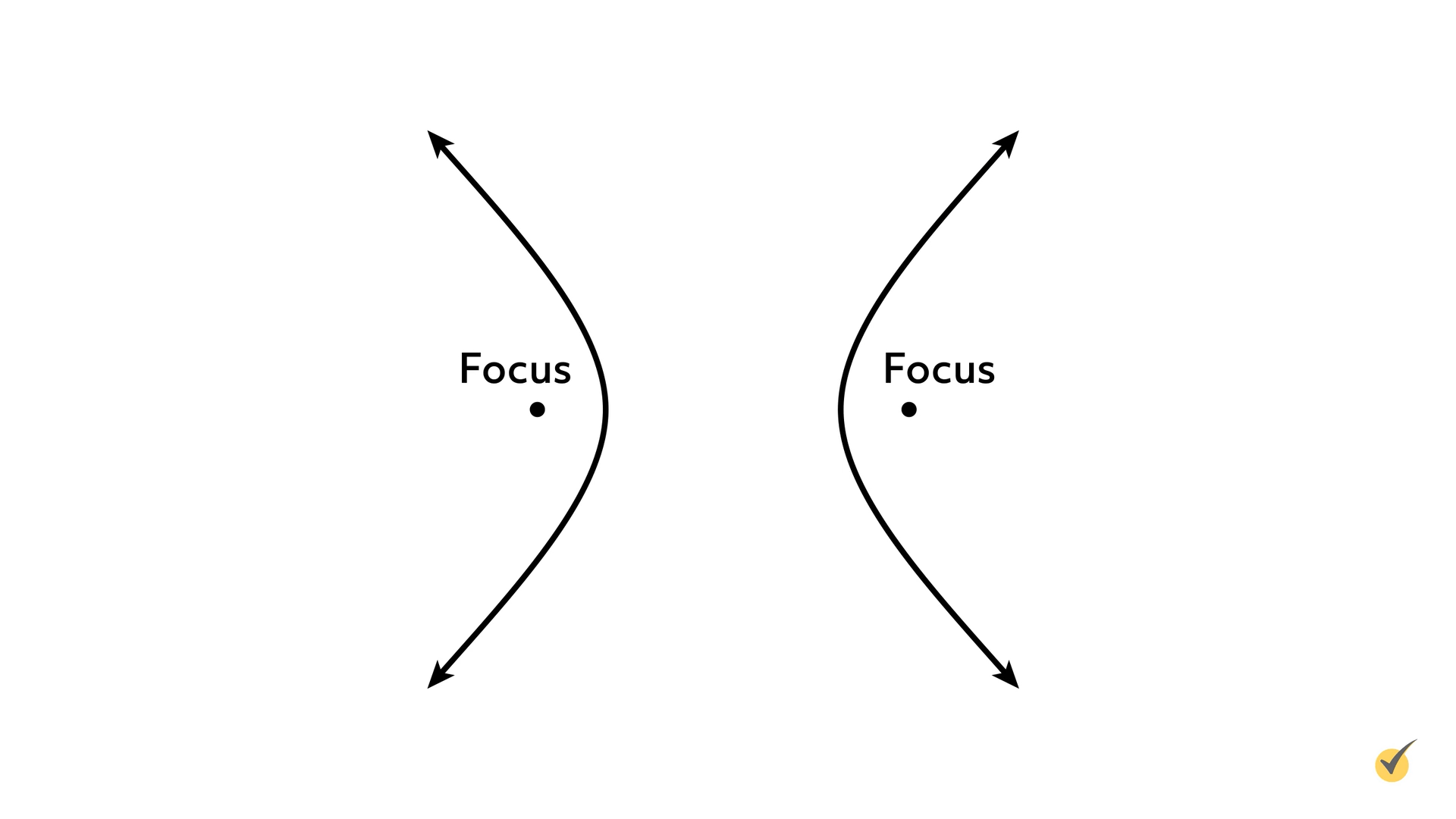
Okay, it definitely doesn’t look much like an ellipse. But it does have two focus points! It also has one of those math-y definitions we all like so much: All the points on the curves of a hyperbola lie such that the difference of the distances from any point to both focus points is a constant.
This means that drawing line segments to any point on the hyperbola will result in the longer one always being the same amount longer than the smaller one. The two line segments will both get longer the farther away from the center of the hyperbola we get, but they get longer at the exact same rate so the difference between them is the same.
Parts of a Hyperbola
There’s a lot more to a hyperbola than its definition and foci though. It has vertices, a center, and asymptotes!
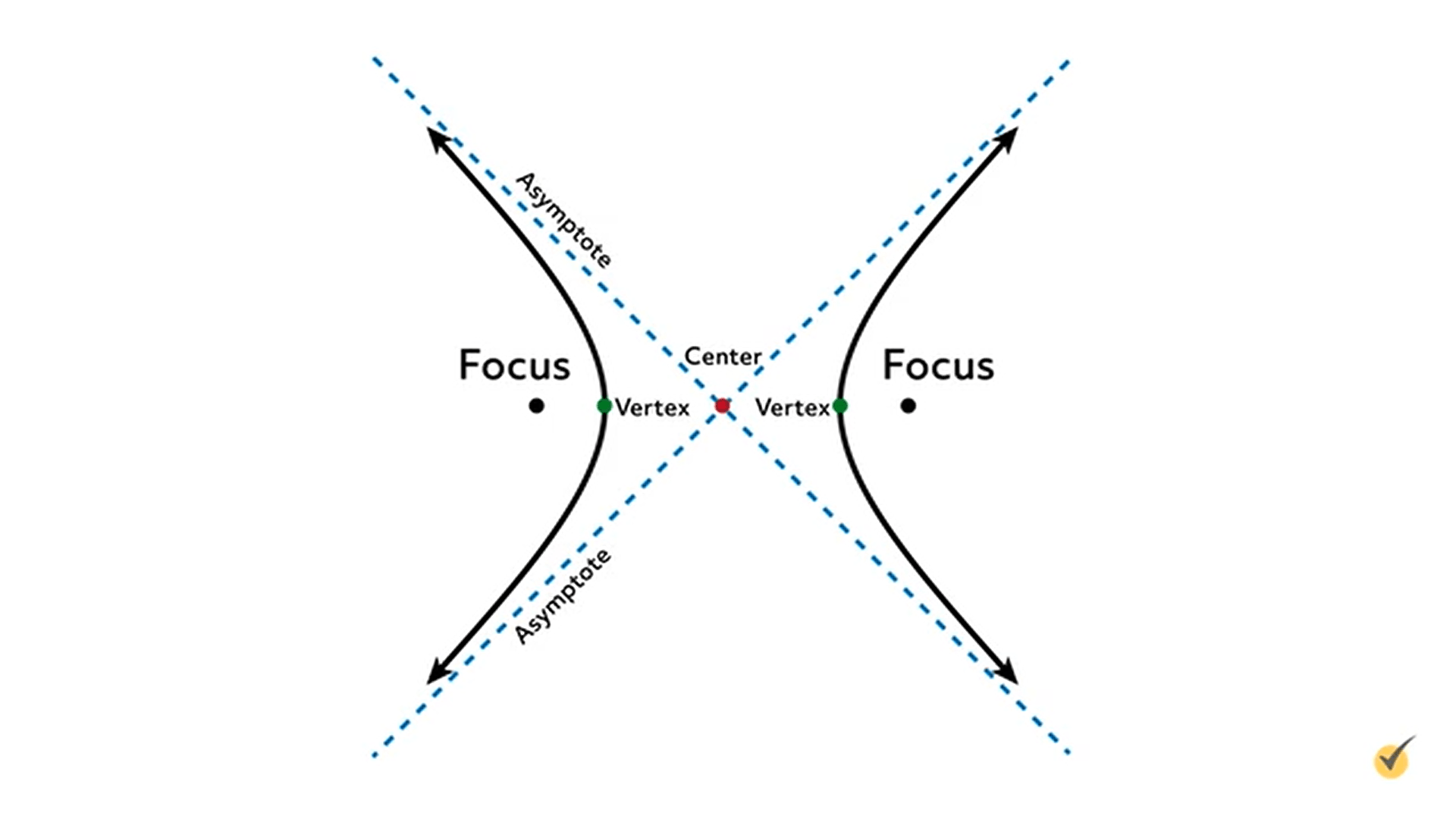
There’s a lot going on here! We can see the two asymptote dashed lines intersect at the center, which, just like in an ellipse or circle, gives us the (\(h\), \(k\)) we need in our equation.
The center is equidistant from the two vertices as well as the two focus points, and all of these points lie on the same horizontal line. That’s why this is a horizontal hyperbola.
The asymptotes serve as guides for our graph of the hyperbola. As the hyperbola stretches out away from the center, each of its curves will get closer and closer to the nearest asymptote but will never touch. We’ll come back to the asymptotes in a minute.
But first, we need to go back to our equation.
Finding a and b
So far we’ve identified how to find \(h\) and \(k\) in this equation by finding the center of the hyperbola. But what about \(a\) and \(b\)? For that, we need to add even more to our drawing:
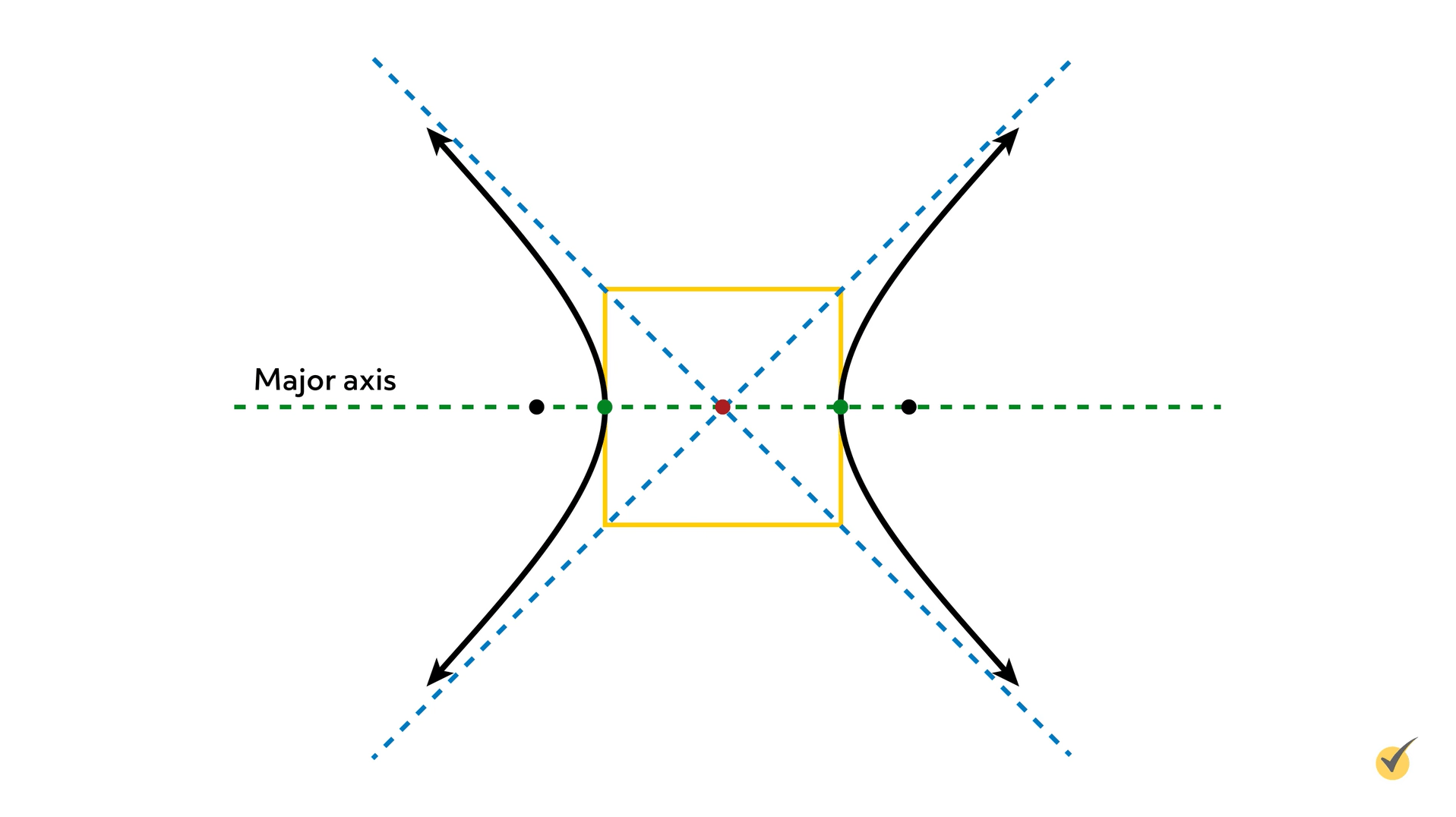
Now we can see the major axis, which has five points on it! The two focus points, shown in black; the two vertex points, shown in green; and the red center point. We can also see a yellow box that intersects the two vertex points at its side midpoints, and also has the asymptotes going directly through its corners. This box helps us find the lengths of \(a\) and \(b\)!
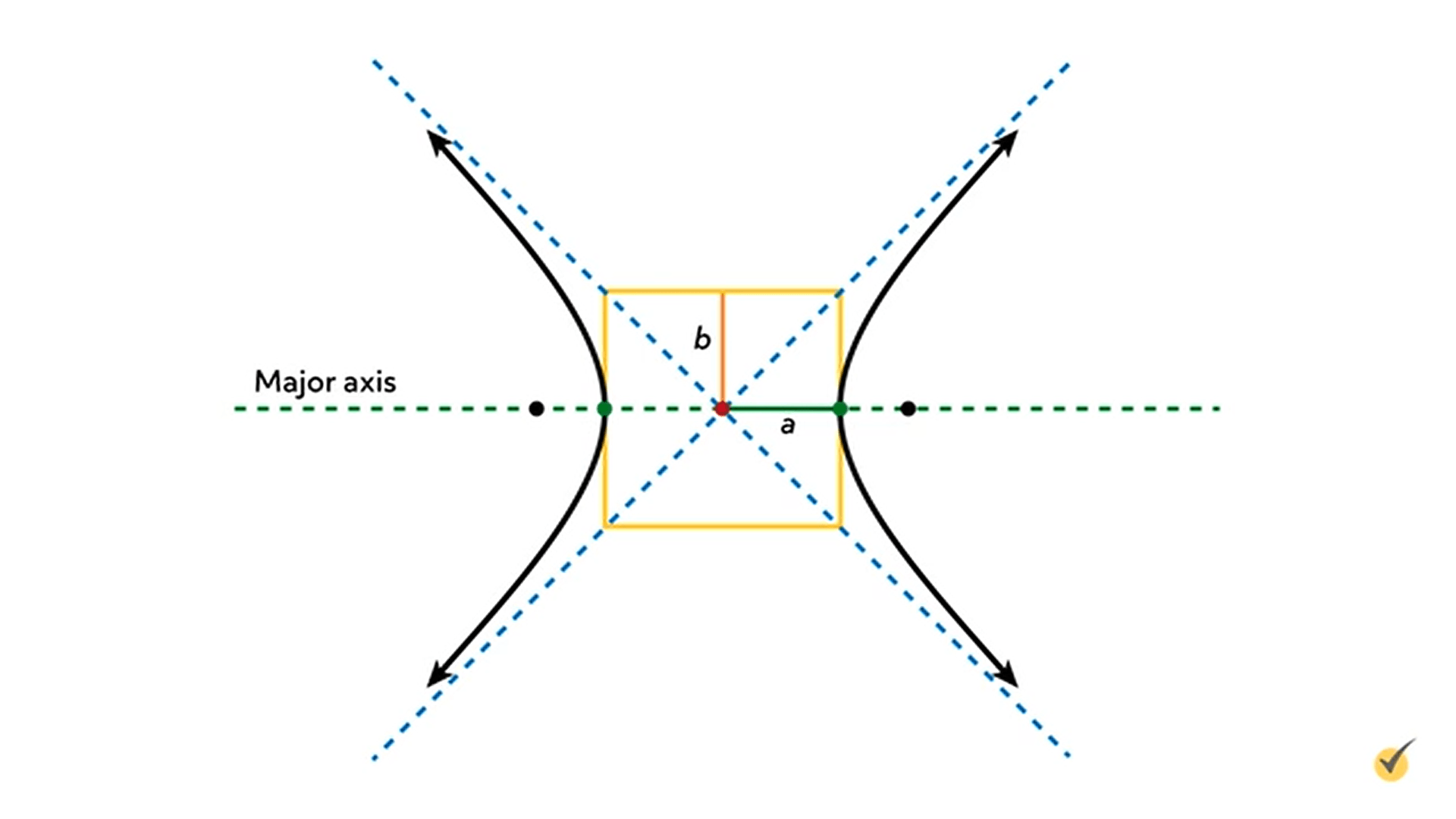
Now we can see our \(a\) and \(b\)! The \(a\) is always on the major axis, which is called the transverse axis.
Asymptote Equations
The major or transverse axis is easy to identify since it has the focus points on it as well as the vertex points. So \(a\) is the distance from the center to either vertex point. And \(b\) is the distance from the center to the top of the box formed by drawing a rectangle that has the asymptotes cutting through its corners.
That accounts for all the variables in our equation. It also allows us to find the equations of our asymptotes. This is easiest when the center of our hyperbola is at the origin, also known as the point (0,0). Here’s the equation for an asymptote when the center is the origin:
You might see it written this way too:
That gives us one of them. Here’s the other:
But what about when the hyperbola is not centered at the origin? Then the formulas look a bit more complicated:
We don’t actually need to find the asymptotes to find the equation of our hyperbola. But there’s actually one more important variable we need to be able to find, and that’s \(c\), which is the distance from the center to the focus points.
Fortunately, we have our old friend the Pythagorean theorem to help us find it from \(a\) and \(b\).
That’s awesome! But why does it work? It turns out that the right triangle we can form by drawing a line segment from either ends of \(b\) and \(a\) has a hypotenuse that’s the same distance as the distance from the center of the hyperbola to either of its focus points.
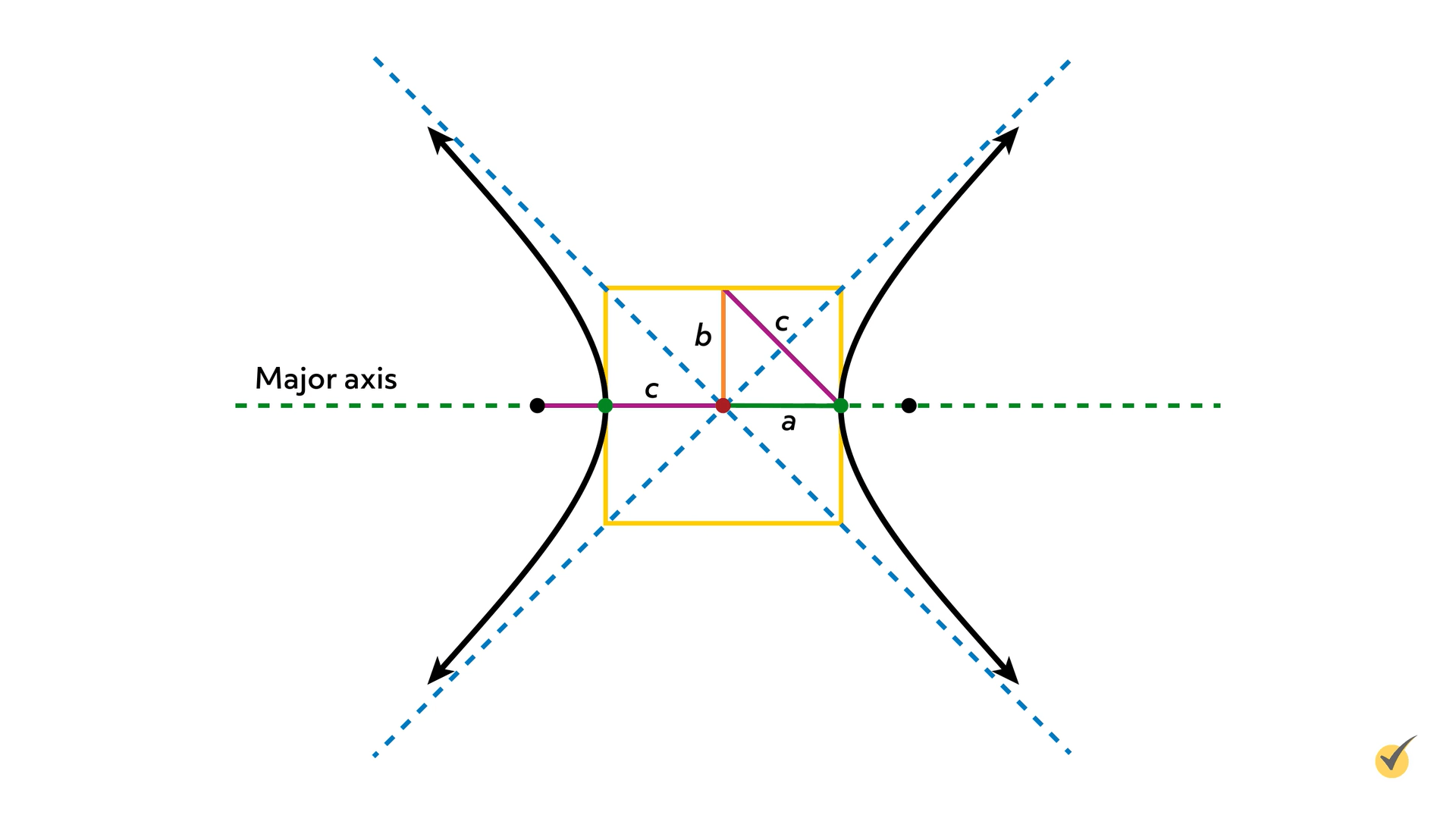
In a math problem, we’re more likely to know the focus points than to know the length of \(b\), so we have to use the Pythagorean theorem to solve for \(b\) instead of for \(c\). If we rearrange the Pythagorean theorem, we can use it this way:
None of this changes too much when our hyperbola is oriented vertically instead of horizontally. Our equation rearranges slightly to:
Notice that the \(y\)-term comes first and is over the \(a^{2}\). That’s because \(a\) is always on the major (or transverse) axis, and with a vertical hyperbola, our major axis is parallel to the \(y\)-axis.
Let’s try a problem that will require us to find the \(h\), \(k\), \(a\), and \(b\) when given focus point and the two vertex points.
What is the equation of a hyperbola that has vertices at (2,5) and (2,-3) and focus points at (2,6) and (2,-4)?
Hint: Sketching the points and then finding the center will help us in finding \(a\) and \(c\), as well as giving us \(h\) and \(k\).
We start with the general equation of a vertical hyperbola that is taller than it is wide. We know to use this one because all the points given are on the same vertical line. Next, we find the center of the hyperbola by finding the midpoint of the two vertex points.
Once we know the center is at the point (2,1), we substitute the \(x\)– and \(y\)-values of the center for \(h\) and \(k\) in our general equation.
To find the value for \(a\), we find the distance between our center that we just found and either of the vertex points, which is a distance of 4 units. To find \(b\), we need to use our focus points to find \(c\) first. Taking the distance from the center to either focus point, we find a distance of 5.
From there, we find that \(b=3\) using the Pythagorean theorem. Now we plug \(a\) into our equation and square it to get our first denominator, which is 16. We do the same thing for \(b\) to find our second denominator is 9. Done!
That’s all there is to it! I hope this review of hyperbolas was helpful! Thanks for watching, and happy studying!