
Right triangle word problem. A ramp with a 30-degree angle from the ground is to be built up to a 2-foot-high platform. What will be the length of the ramp? How far from the platform will it extend to the nearest inch? With problems like these, it’s very helpful to draw a picture.
We have our ramp that makes a 30 degree angle with the ground. Let’s start with that. Here’s the ground. Here’s our 30-degree angle. It’s to be built up to a 2-foot-high platform. Then here we have a platform, and it’s 2 feet high above the ground. There’s a right angle there perpendicular to the ground.
The first question is; what will be the length of the ramp? This is what we’re trying to find. Well before I start to find \(x\), I first want to fill in what this angle is. You might already know that since we have a 30-degree angle and a 90-degree angle that this angle has to be 60 degrees.
But, if you didn’t know that you could find it, because there are 180 degrees in a triangle. If you add 30 to 90 you get 120. 180 minus 120 leaves you with 60 degrees for that third angle. Now that we know it’s a 30-60-90 triangle, we can apply our 30-60-90 rules to finding the length of our ramp.
Our ramp is across from the 90 degree angle, therefore that’s our hypotenuse. The side we know, the leg we know is across from the 30 degree angle, so it’s our shorter leg. The hypotenuse of a 30 60 90 triangle is twice as long as the shorter leg.
Our hypotenuse again, we’re using\(x\) for, equals 2 times the shorter leg which is that 2 foot side. 2 times 2 feet. Which means \(x\) is 4 feet. Therefore, the length of the ramp is 4 feet. We’ve answered the first question. Then they asked; how far from the platform will it extend, how far from the platform will the ramp extend?
Now they’re asking us to find that length. \(y\) is across from our 60 degree angle so that’s our longer leg. The longer leg of a 30-60-90 triangle is the square root of three times the shorter leg. Our longer leg again is \(y\) equals the square root of three times, our shorter leg is still that two foot length.
\(y\) is 2 square roots of 3 feet. They didn’t ask us for the answer in feet they asked to the nearest inch. The first thing I’m going to do is convert 2 square roots of 3 feet into inches by multiplying by 12. \(y\) is 2 square roots of 3 times 12, since there are 12 inches in one foot, which is 24 square roots of 3 inches.
They didn’t ask for it in simplest radical form, so then we’d actually want to calculate what 24 square root three inches is, and it’s about 42 inches. Therefore, how far from the platform will the ramp extend? The ramp will extend about 42 inches from the platform. There we have it.
Frequently Asked Questions
Q
What is a right triangle?
A
A right triangle is a triangle that has a 90° (right) angle.
Ex. 
Q
How do you find the angle of a right triangle?
A
Find the angle of a right triangle given two side lengths by using these formulas (SOH-CAH-TOA):
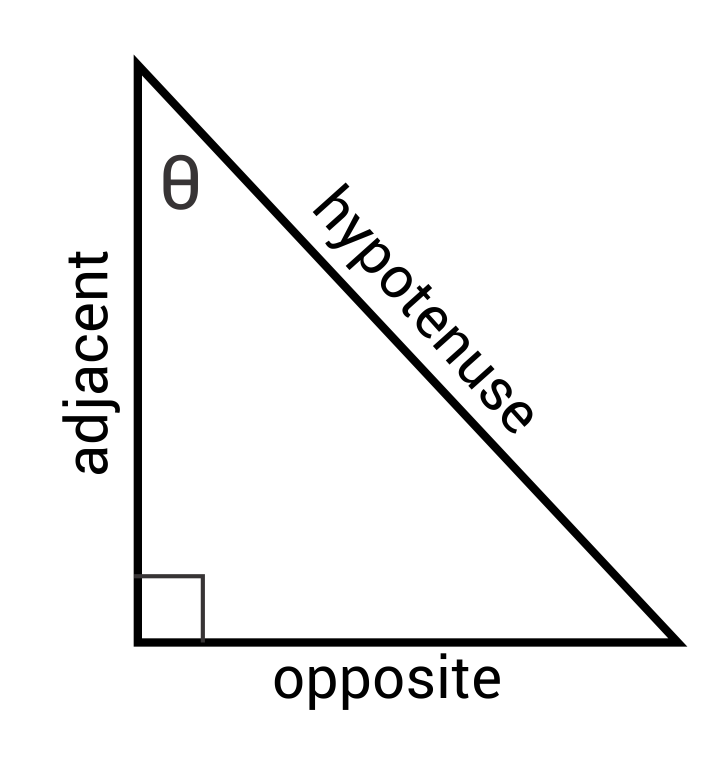
\(sinθ=\frac{opposite}{hypotenuse}\) \(cosθ=\frac{adjacent}{hypotenuse}\) \(tanθ=\frac{opposite}{adjacent}\)
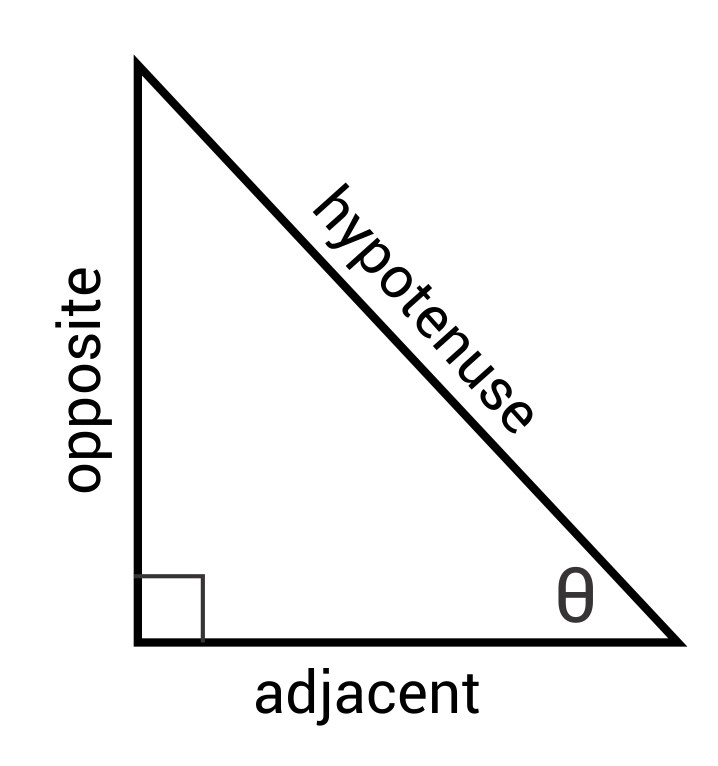
Ex. Find ϴ for this triangle:
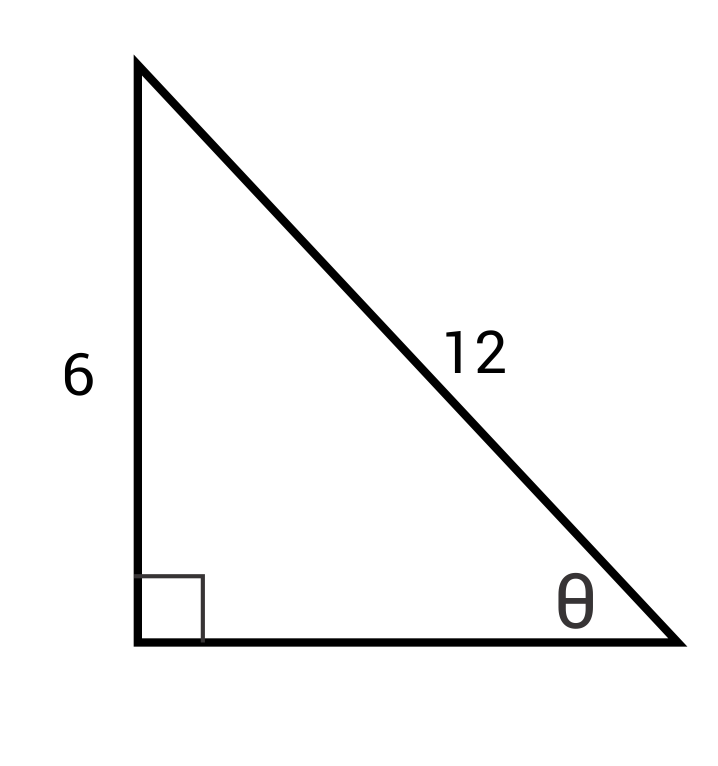
\(sinθ=\frac{6}{12}\)
\(sinθ=\frac{1}{2}\)
\(θ=sin^{-1}(\frac{1}{2})\)
\(θ=30°\)
Q
How do you find the area of a right triangle?
A
Find the area of a right triangle by multiplying its base times its height and dividing by 2.
\(A=\frac{1}{2} bh\)
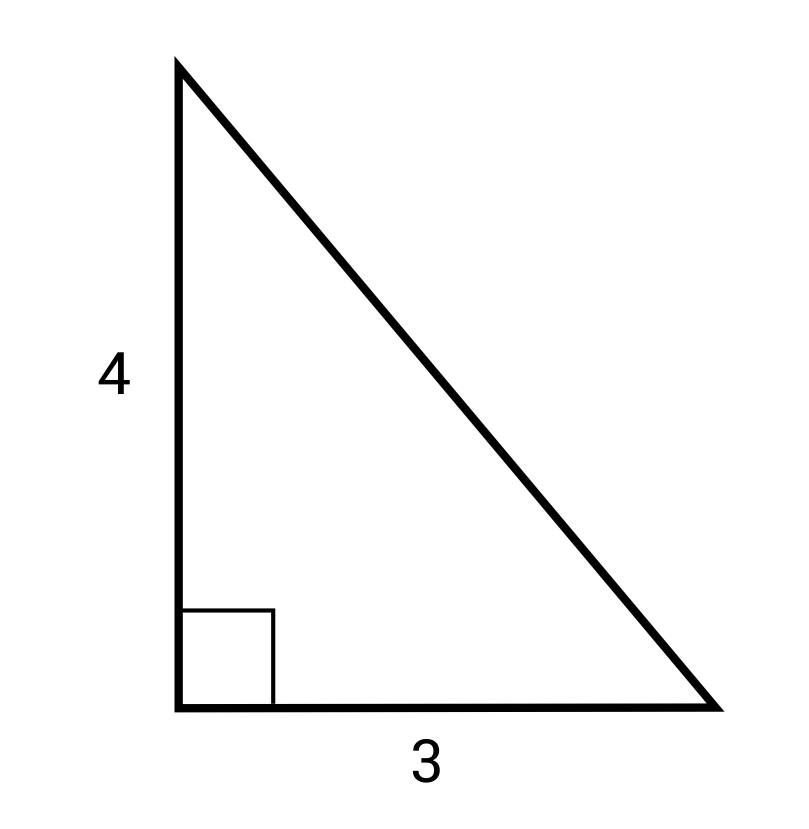
Ex. What is the area of this right triangle?
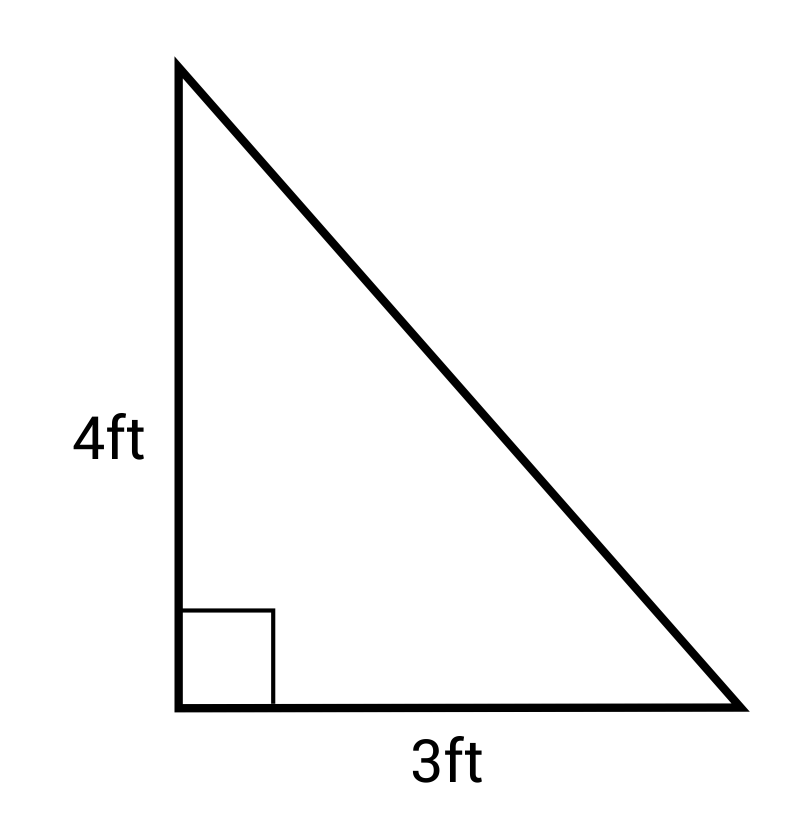
\(A=\frac{1}{2} bh=\frac{1}{2} (3)(4)=6 ft^2\)
Q
How do you find the sides of a right triangle?
A
Find the sides of a triangle using the following formulas (SOH-CAH-TOA):
\(sinθ=\frac{opposite}{hypotenuse}\) \(cosθ=\frac{adjacent}{hypotenuse}\) \(tanθ=\frac{opposite}{adjacent}\)
Ex. Solve for x:
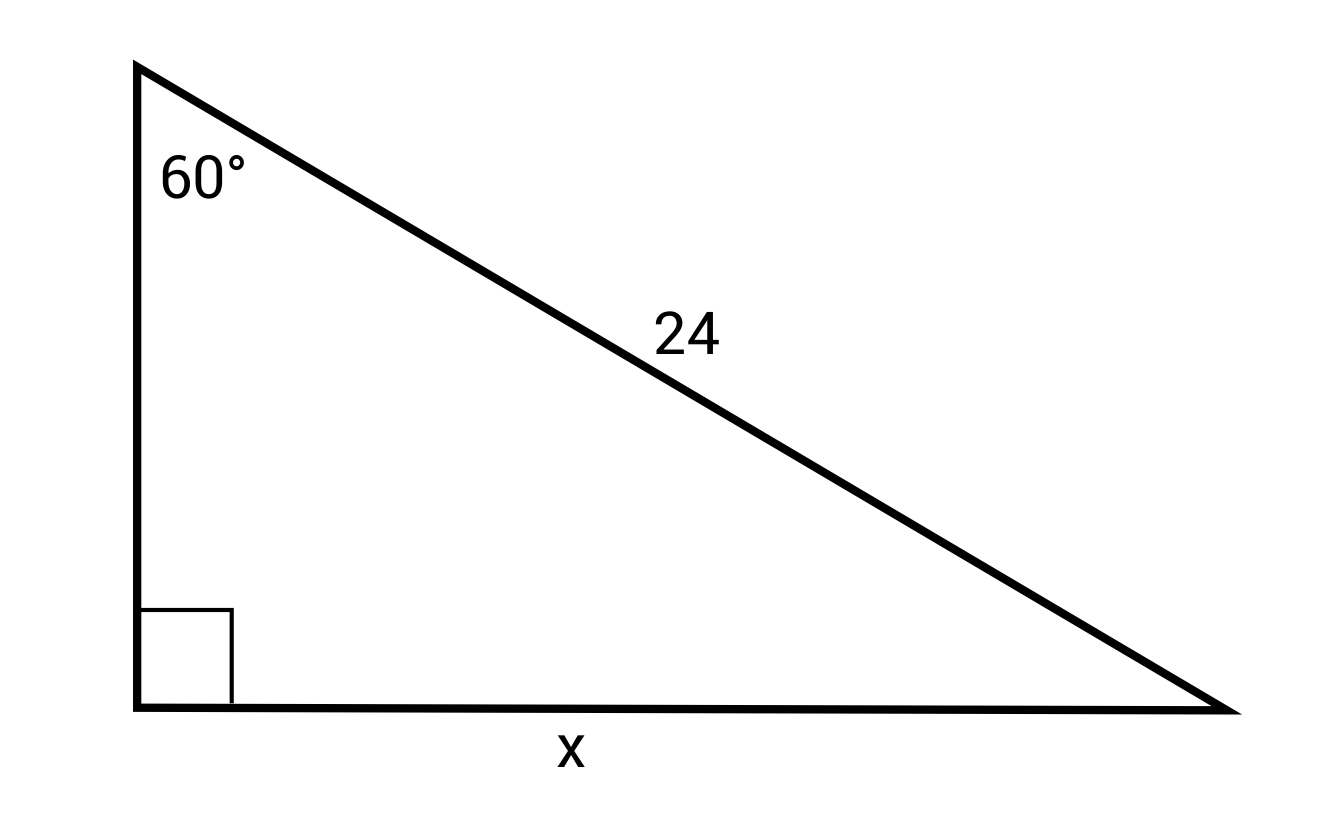
\(sin60°=\frac{x}{24}\)
\(x=24 sin60°≈20.78\)
Q
How do you find the hypotenuse of a right triangle?
A
Find the hypotenuse (c) of a right triangle given the other two side lengths (a and b) by using the Pythagorean Theorem:
\(a^2+b^2=c^2\)
Ex. What is the hypotenuse of this right triangle?
\((4)^2+(3)^2=c^2\)
\(16+9=c^2\)
\(25=c^2\)
\(5=c\)
Q
How do you find the missing side of a right triangle?
A
Find the missing side of a right triangle by using the Pythagorean Theorem: c^2=a^2+b^2, where c is the hypotenuse and a and b are legs of the triangle.
Ex. Find the missing side length.
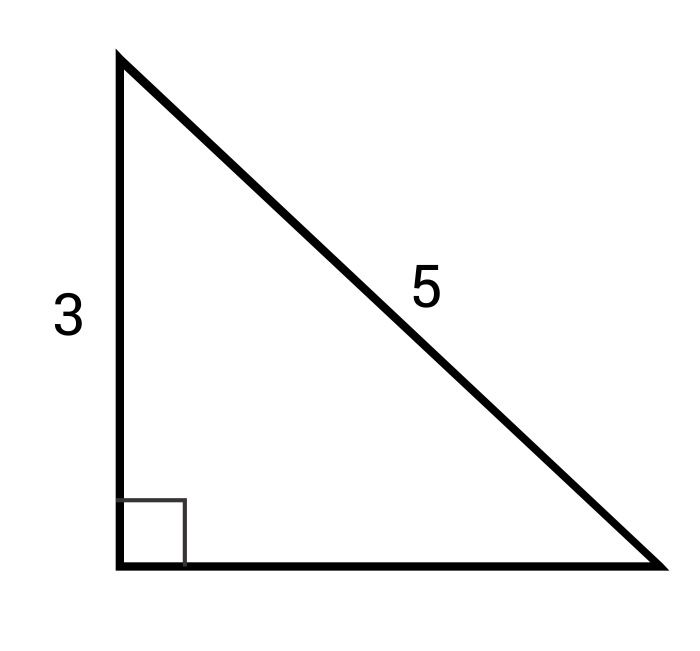
\(c^2=a^2+b^2\)
\(5^2=3^2+b^2\)
\(25=9+b^2\)
\(16=b^2\)
\(4=b\)