
Hello, and welcome to this video about the sum of interior angles of polygons! In this video, we will explore different types of polygons and how to find the sum of their interior angles.
Let’s learn about the sum of interior angles!
What are Polygons?
Polygons are everywhere we look. The board in the classroom is a rectangle, and the floor tiles are squares. The yield road sign is a triangle, and the stop sign is an octagon.
A polygon is a two-dimensional figure that is formed when line segments meet to create a closed shape. We name polygons based on the number of sides. A triangle has 3 sides, a quadrilateral has 4 sides, and an octagon has 8 sides.
Today we want to learn about how to find the sum of interior angles of any polygon. This is a skill we use in our daily life. When laying tile or even choosing a tile, which will always be shaped like a polygon, we will use the measure of the angles to determine how the tiles will fit with each other.
Triangles
We will start with a triangle, since it is the polygon with the least number of sides. To find the sum of the interior angles of this triangle, I am going to rip off all the angles and then put them back together so the vertices meet.
As you can see, when we line up the three angles, they form a straight line, and we know that a straight angle is 180°. Now let’s look at a polygon with four sides, a rectangle, which is a type of quadrilateral, a polygon with four sides. As you can see, I can use a line segment to connect the opposite angles, and this will turn my rectangle into two triangles.
Since I know the sum of the interior angles of one triangle, we will multiply 180 by two to get the sum of the interior angles of a rectangle, 360°, or the sum of the interior angles of any quadrilateral.
Pentagons
A polygon with 5 sides is called a pentagon. As you can see, I was able to create 3 triangles inside the pentagon. To find the sum of the interior angles of the pentagon, we will multiply 180 by 3, which is 540°.
As you can imagine, finding the sum of the interior angles of a polygon using this method of creating triangles can become quite tedious if we are dealing with a polygon with 25 sides.
Patterns
Let us take a closer look and see if we can see a pattern. We will organize the information we have gathered so far into a table.
| Shape | Number of Sides | Sum of interior angles | Pattern |
|---|---|---|---|
| Triangle | 3 | 180° | 1 triangle \(\times \) 180° |
| Quadrilateral | 4 | 360° | 2 triangles \(\times \) 180° |
| Pentagon | 5 | 540° | 3 triangles \(\times \) 180° |
The closer look at the pattern shows that we always multiply two less than the number of sides the polygon has by 180, so we can create a formula, where \(n\) represents the number of the sides of the polygon:
Hexagons
Let’s test our formula:
What is the sum of the interior angles of a hexagon?
We know that a hexagon has 6 sides. Therefore, \((6 – 2)\times 180 = 720°\), which is the sum of the interior angles of a hexagon.
Let us confirm our finding by drawing a hexagon and dividing it into triangles. As you can see, there are 4 triangles and \(4\times 180 = 720\).
Other Problems
Now that we have a formula, we can solve many more types of problems.
Here’s another example:
The sum of the interior angles of a polygon is 1,080°. How many sides does the polygon have?
We can use the formula and substitute what we have \((n-2)\times 180=1,080\). Since \(n\) represents the number of sides, we can use our algebra skills to solve for \(n\). First, we divide both sides by 180, which will result in, \(n-2=6\). Then we add 2 to both sides to get \(n=8\). Therefore, the polygon with interior angles adding to 1,080° is an octagon.
Now that we’ve learned how to find the sum of the interior angles of a polygon, let’s try to find the measure of one angle of a regular polygon. As you recall, a regular polygon is equiangular and equilateral, which means all the angles have the same measure and the sides have the same length. Since the formula, \((n-2)\times 180\), gives us the sum of the interior angles, if we divide by the total by the number of angles, it will give us the measure of one angle. Therefore:
Let’s take a look at an example.
The measure of one interior angle of a regular polygon is 150°. How many sides does the polygon have?
We will start by substituting what we know into the formula, \(\frac{(n-2)180}{n}=150\). We will eliminate the fraction by multiplying both sides by \(n\) to get \((n-2)180=150n\). Simplify using the distributive property, \(180n – 360 = 150n\). Solve for \(n\) by combining like terms, \(30n=360\). Then isolate the variable by dividing both sides by 30 to get \(n=12\). Therefore, the regular polygon, where the measure of one interior angle is 150° has 12 sides, which is called a dodecagon.
Now let’s talk about the exterior angles. When we extend the sides of a polygon, the angle created on the outside is called an exterior angle. As you can see, the exterior angle and the interior angle form a straight angle.
Now, we will consider this regular triangle. This means that the measure of each interior angle is 60°. If the interior angle is 60°, then the exterior angle must be 120°. We can add the measure of the 3 exterior angles for this triangle to find the sum of the exterior angles of a triangle, which is 360°.
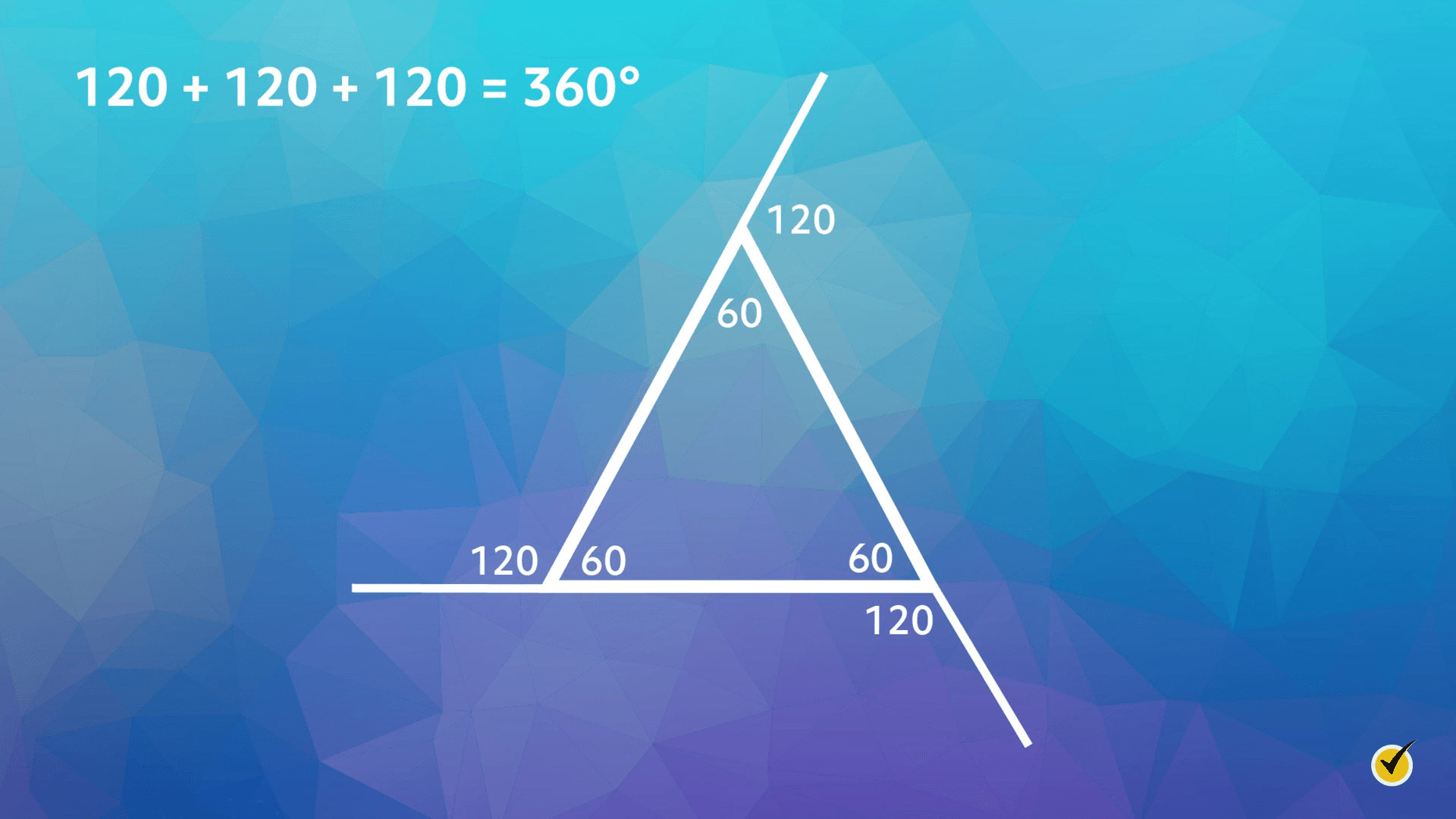
Now let’s take a look at a rectangle. We will do the same thing and extend each side. We know that the interior angles are 90°, which makes the exterior angles also 90°. We will add the exterior angles to find the sum of the exterior angles of a rectangle, which is \(90\times 4=360°\).
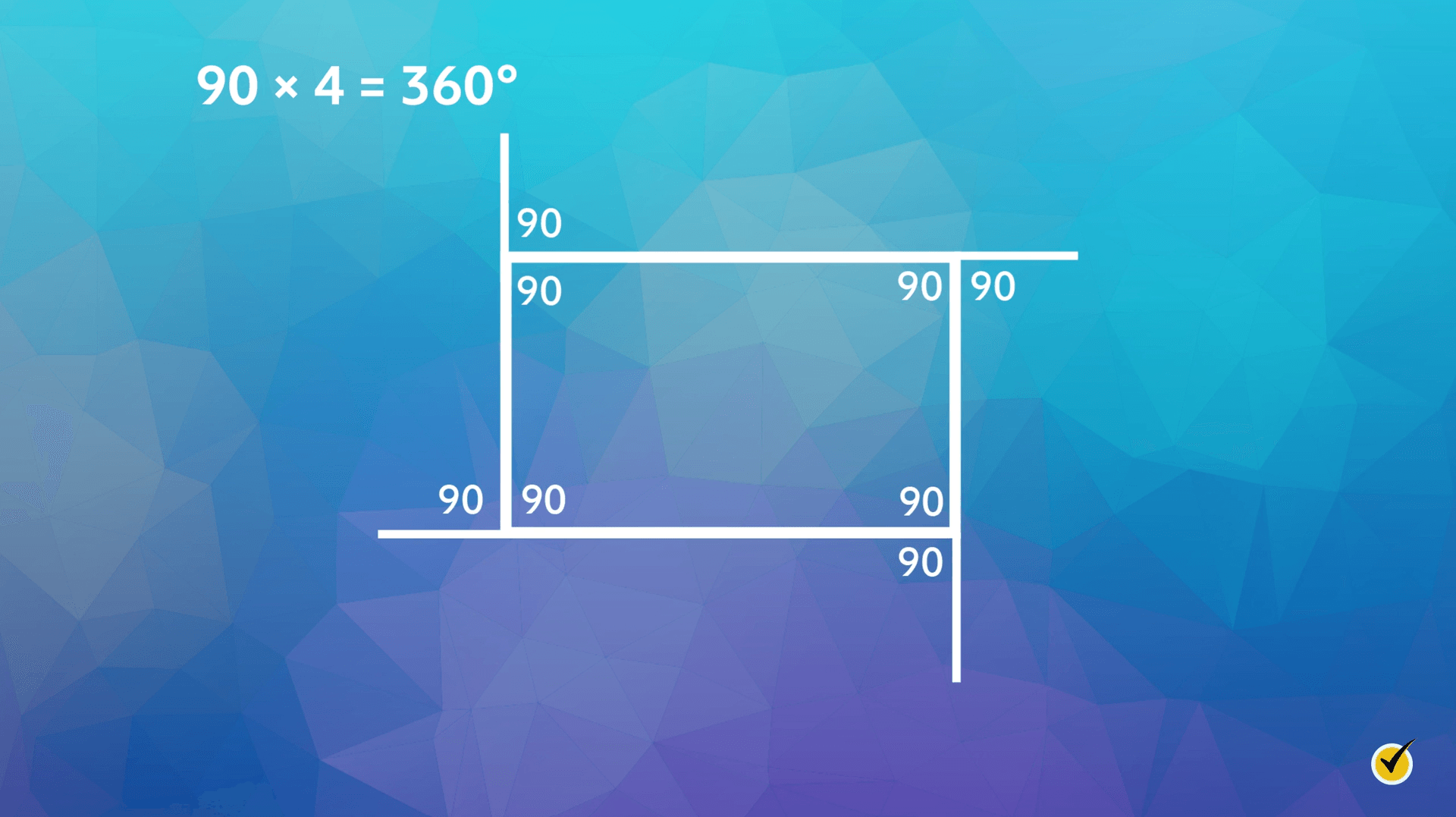
Based on our two experiments, we can conclude that the sum of the exterior angles of any polygon is always 360°. This knowledge can also help us solve problems.
For example, the measure of one exterior angle of a regular polygon is 72°. How many sides does this regular polygon have?
Since this is a regular polygon and we know that the sum of the exterior angles of all polygons is 360°, we can simply create the equation \(\frac{360}{n}=72\). Then we solve for \(n\) to find the number of sides. We will first eliminate the fraction, \(72n=360\). Then divide both sides by 72 to isolate the variable, which gives us that \(n=5\). Therefore, the polygon has 5 sides, which is also called a pentagon.
I hope you enjoyed this video about the sum of the interior angles of polygons. Thanks for watching, and happy studying!
Sum of Interior Angles Practice Questions
What is the sum of interior angles of any nonagon, or nine-sided polygon?
In order to find the sum of the interior angles of a polygon, use the formula \((n-2)\times180\), where \(n\) is the number of sides of the polygon. In this case, the polygon of concern has nine sides, so the sum of interior angles is equal to \((9-2)\times180\), or \(7\times180\), which equals \(1{,}260\) degrees.
What polygon has a sum of interior angles equal to 2,160°?
Remember that the sum of interior angles of a polygon is equal to \((n-2)\times180\). Set this equal to \(2{,}160\), and then solve for \(n\) to determine how many sides the polygon has.
\((n-2)\times180=2{,}160\)
Divide both sides by \(180\).
\((n-2)=\frac{2{,}160}{180}\)
\(n-2=12\)
Finally, add \(2\) to both sides.
\(n=14\)
So fourteen-sided polygons have a sum of interior angles equal to \(2{,}160\)°.
How many degrees are in one interior angle of a regular decagon (ten-sided polygon)?
Since the interior angles of regular polygons are all equal in measure, the measure of one of the angles can be found by dividing the sum of interior angles by \(n\).
\(\frac{(n-2)\times180}{n}\)
The problem states that this polygon has ten sides, so plug \(n=10\) into the formula.
\(\frac{(10-2)\times180}{10}=\frac{8\times180}{10}=144°\)
Each interior angle of a regular decagon has measure equal to \(144°\).
Chalice is designing a playground merry-go-round in the shape of a regular polygon, of which each interior angle is equal to \(135°\). How many sides does the merry-go-round have?
Since the measure of one interior angle of a regular polygon can be found with the formula \(\frac{(n-2)\times180}{n}\), the number of sides can be determined by solving for \(n\). First, set this formula equal to \(135°\).
\(\frac{(n-2)\times180}{n}=135\)
Multiply both sides by \(n\).
\((n-2)\times180=135n\)
Multiply out the left side to get:
\(180n-360=135n\)
Then add \(360\) and subtract \(135n\) from both sides.
\(180n=135n+360\)
\(45n=360\)
Divide both sides by \(45\).
\(n=8\)
The merry-go-round has eight sides.
Reagan is designing some table legs in a wood shop. Each leg is shaped with an equal number of sides such that the exterior angles are all equal to \(24°\). How many sides does each leg have?
The exterior angles of a polygon must add up to \(360°\). Since this problem concerns regular polygons, each angle is equal in measure. Because of this, you can use the formula \(\frac{360}{n}=24°\) to solve for the number of sides.
Multiply both sides by \(n\), then divide both sides by \(24\).
\(360=24n\)
\(\frac{360}{24}=n\)
\(15=n\)
This means the table legs each have \(15\) sides.