Adjacent Angles
Definition:
In geometry, two angles are adjacent if they have a common side and a common vertex. In other words, adjacent angles are directly next to each other and do not overlap.
Adjacent Angles Examples:
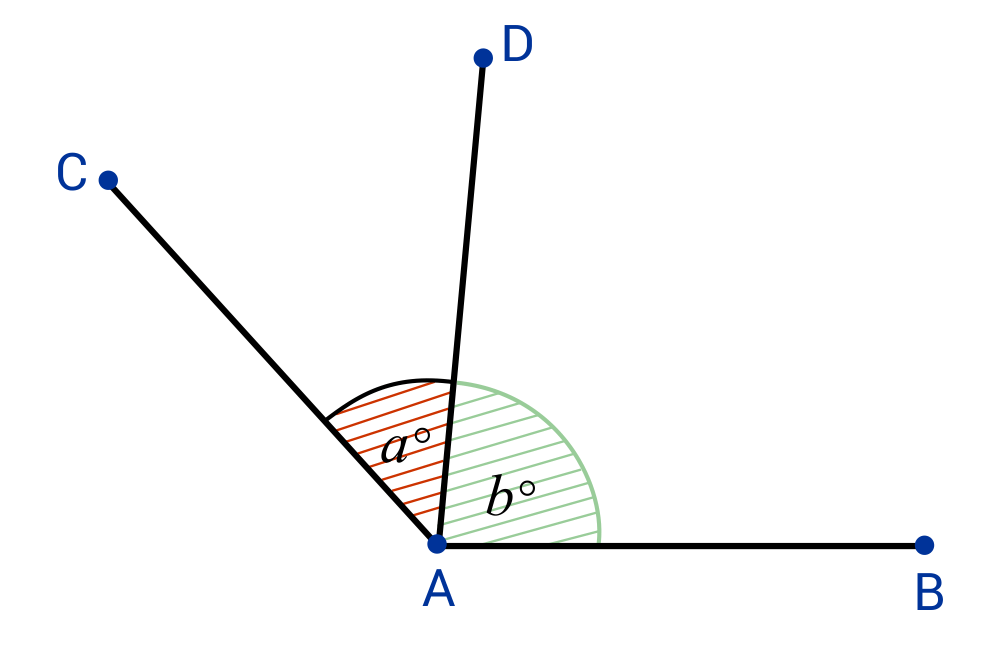
In our first example, ∠a is adjacent to ∠b. They share a common vertex, which is the corner point A. They also share a common side, line AD. ∠a and ∠b are adjoined by line AD, but they do not overlap.
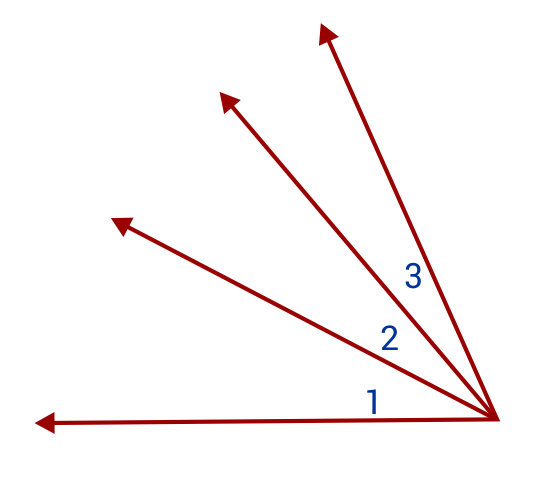
In our second example, we see ∠1, ∠2, and ∠3. We see that ∠1 and ∠2 are adjacent because they have a common vertex and a common side. We see the same thing with ∠2 and ∠3, which also share a vertex and one side. Let’s consider ∠1 and ∠3. Although they share a vertex, they are not adjacent because they do not have a common side.
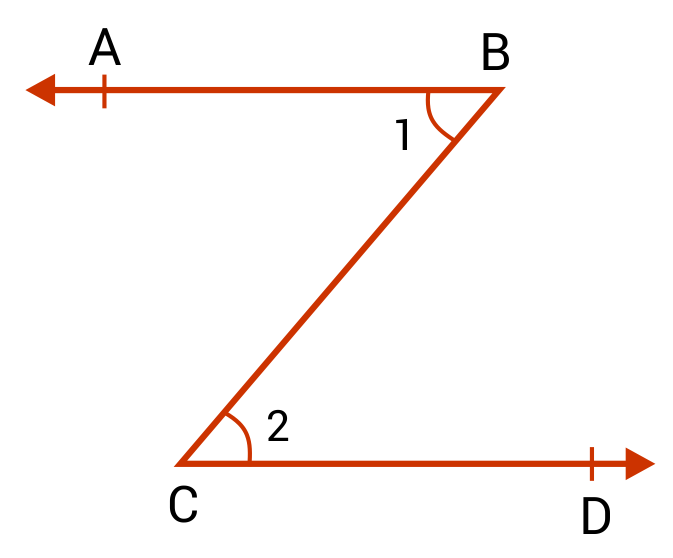In our last example, we see two angles, ∠1 and ∠2. Both angles share one side, line BC. However, these angles are not adjacent because they do not share a vertex.
What are adjacent angles?
Based on our definition and the above examples, we can conclude that all pairs of adjacent angles share two properties: (1) a common vertex and (2) a common side. If they are missing one of these components, then they are not adjacent. We can classify pairs of angles as adjacent or not adjacent by looking for these two properties.
There are many special relationships between pairs of angles. Identifying adjacent angles will help you recognize other angle relationships, such as supplementary and complementary angles.
There are many classifications for types of angles and the different relationships that angles have with each other. One such relationship is adjacency.
The word “adjacent” means “next to,” so it makes sense that two angles are considered adjacent if they are next to each other!
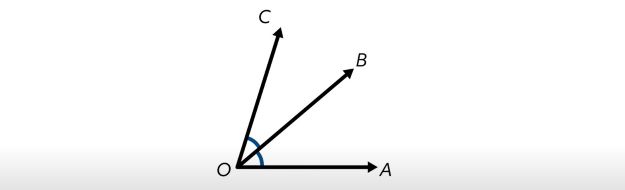
Here, we can see that \(\angle COB\) is next to \(\angle BOA\), making them adjacent. Formally, two requirements must be met for two angles to be considered adjacent. First, the angles must share the same vertex, or corner point. Here, \(O\) is that shared vertex. Second, the two angles must share one common side that lies between them. In this case, that common side is the ray from \(O\) to \(B\).
Angles that overlap cannot be adjacent. For example, angles a and b shown here are not adjacent because they overlap.
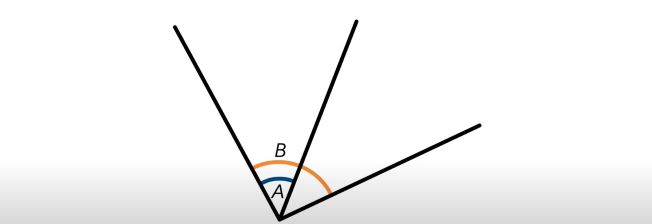
Let’s take a look at some more angles. In this diagram, which pairs of angles are adjacent?
Starting from the left, we can see that angles 1 and 2 share a common vertex and a common side. For this reason, they are adjacent. The pair of angles 2 and 3 also share a common vertex and common side, making them adjacent as well. But what about angles 1 and 3? While these angles still share a common vertex, they have no side in common, so they are not adjacent.
Let’s now consider angle 4. Is it adjacent to any of the other angles? While it does share a common side with angle 3, they do not have the same vertex. For this reason, angles 3 and 4 are not adjacent. Angle 4 is also not adjacent to angles 1 and 2 because it has neither a common vertex nor a common side between them.
Being able to identify adjacent angles by their common vertex and common side will come in handy in future lessons when looking for complementary angles, which are angles that add up to 90°, and for supplementary angles, which are angles adding up to 180°.
I hope that this video was helpful. Thanks for watching, and happy studying!
Adjacent Angle Practice Questions
Which of the following statements is true?
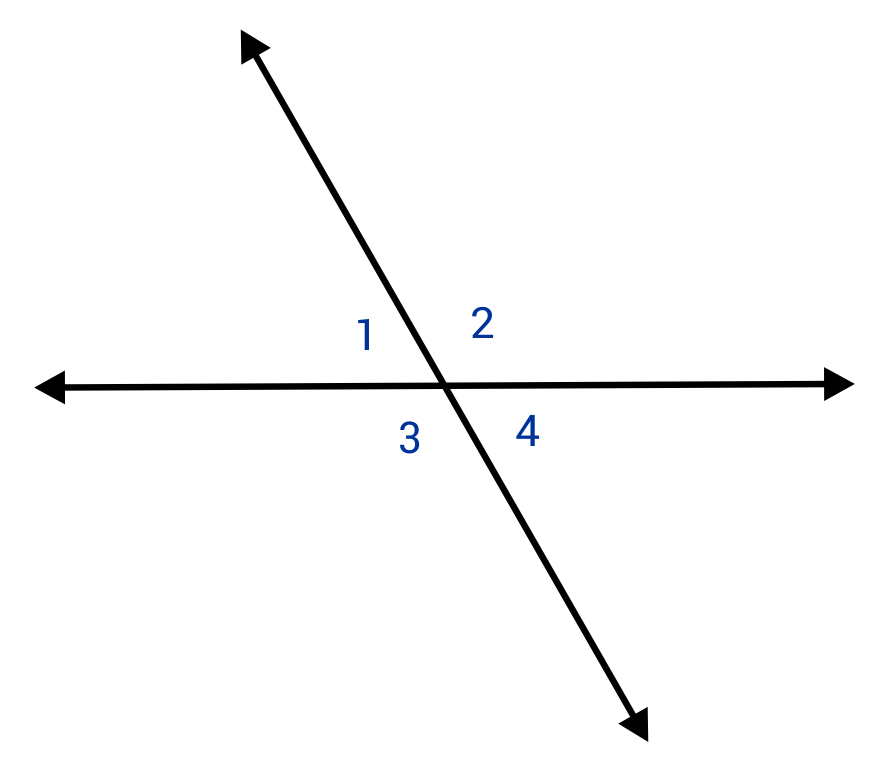
B is correct because ∠3 and ∠4 have a common vertex and side, the two defining characteristics of adjacent angles. A is incorrect because ∠1 and ∠4 do not have a common side. C is incorrect because ∠1 and ∠2 have a common side and vertex. Therefore, they are adjacent. D is incorrect because ∠2 and ∠3 do not have a common side.
Which angles are adjacent?
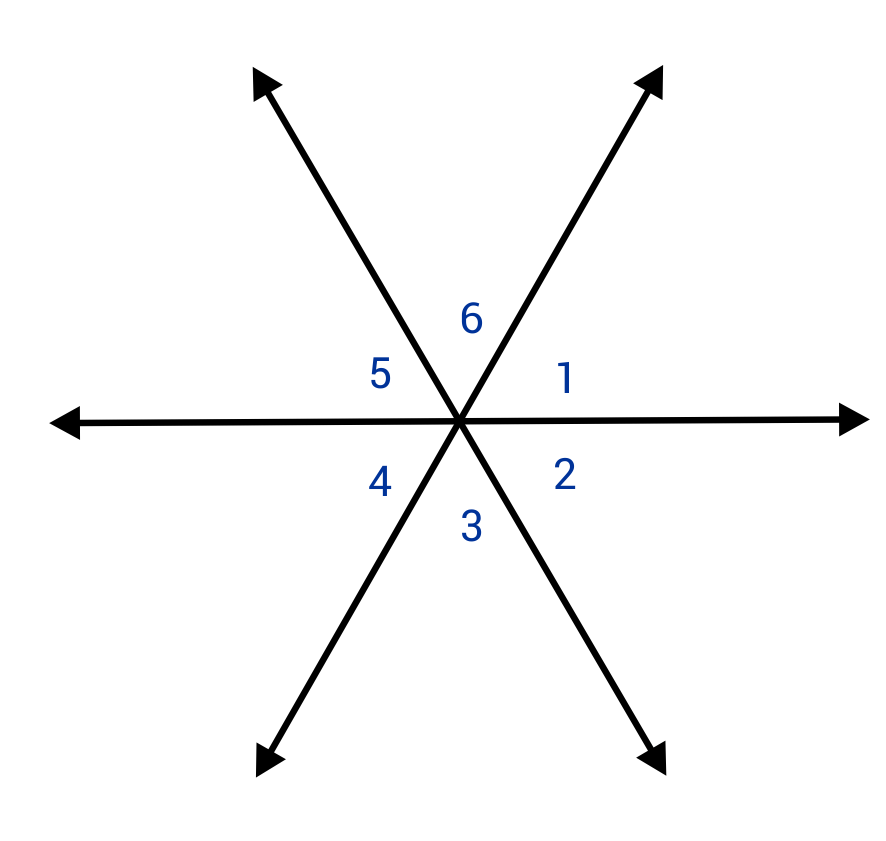
D is the correct answer because ∠2 and ∠3 share one side and a vertex, which are the two necessary components of adjacent angles.
Which angles are not adjacent?
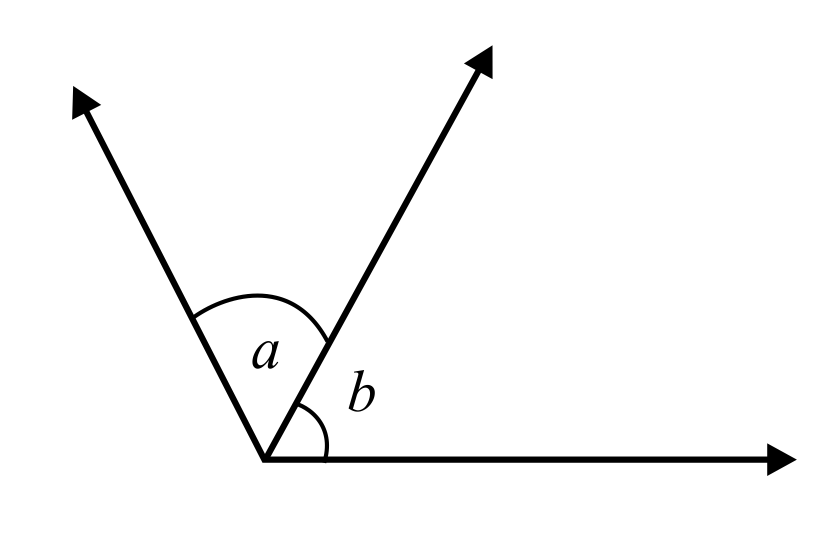
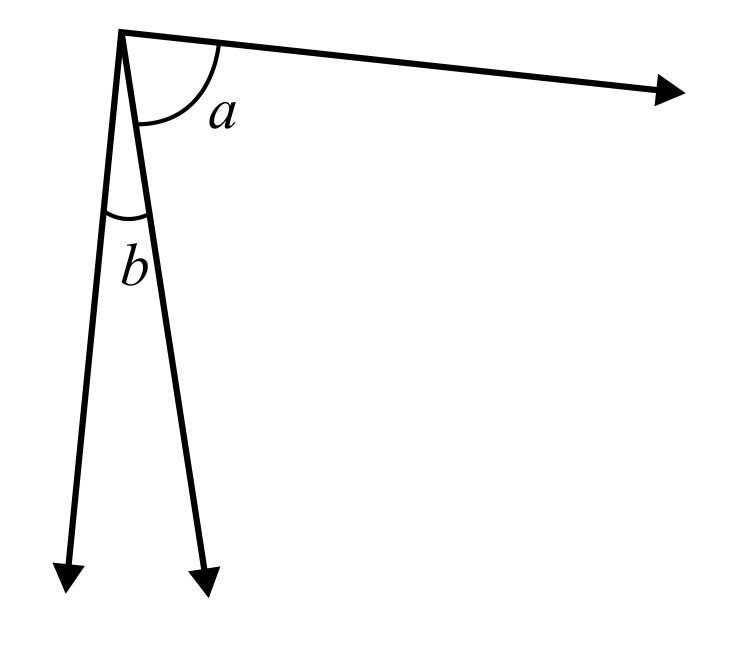
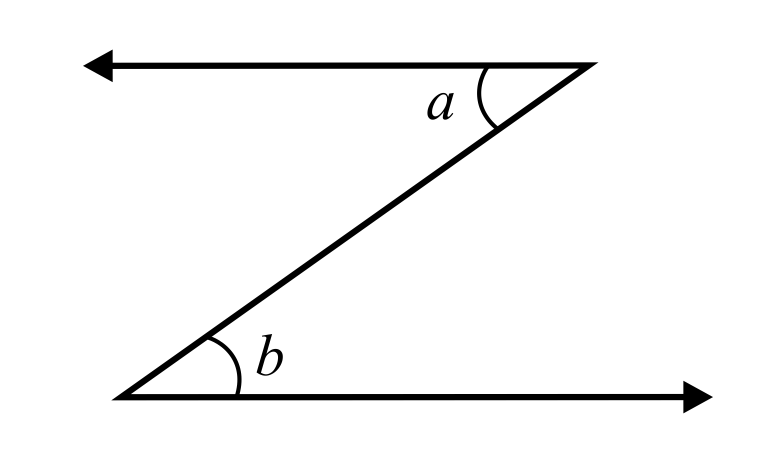
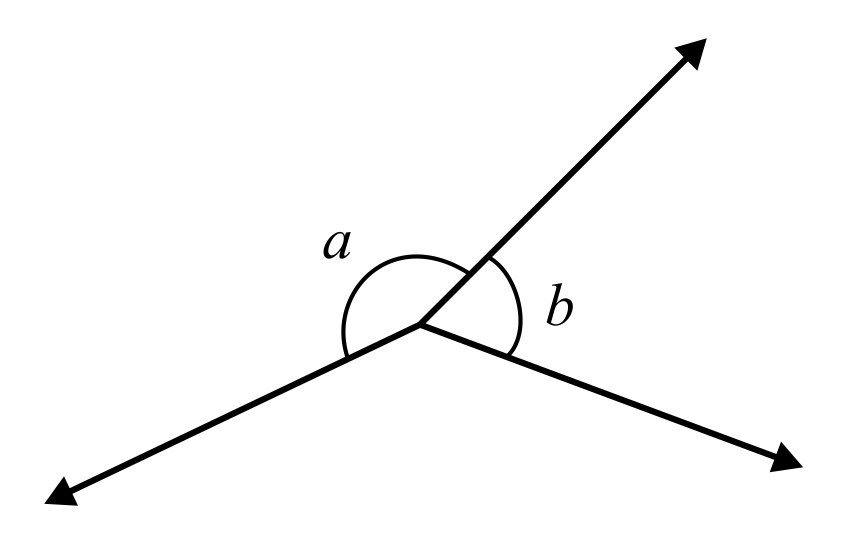
C is the correct answer because ∠a and ∠b because although they share a common side, they have two different vertices. Therefore, they are not adjacent. Choices A, B, and D are incorrect because they all show angle pairs with common sides and a common vertex.
Juan is studying leaf veins and notices adjacent angles in the plant structure. He draws the diagram below and records four pairs of adjacent angles. One of Juan’s adjacent angle pairs is incorrect. Based on the diagram, which pair of angles is not adjacent?
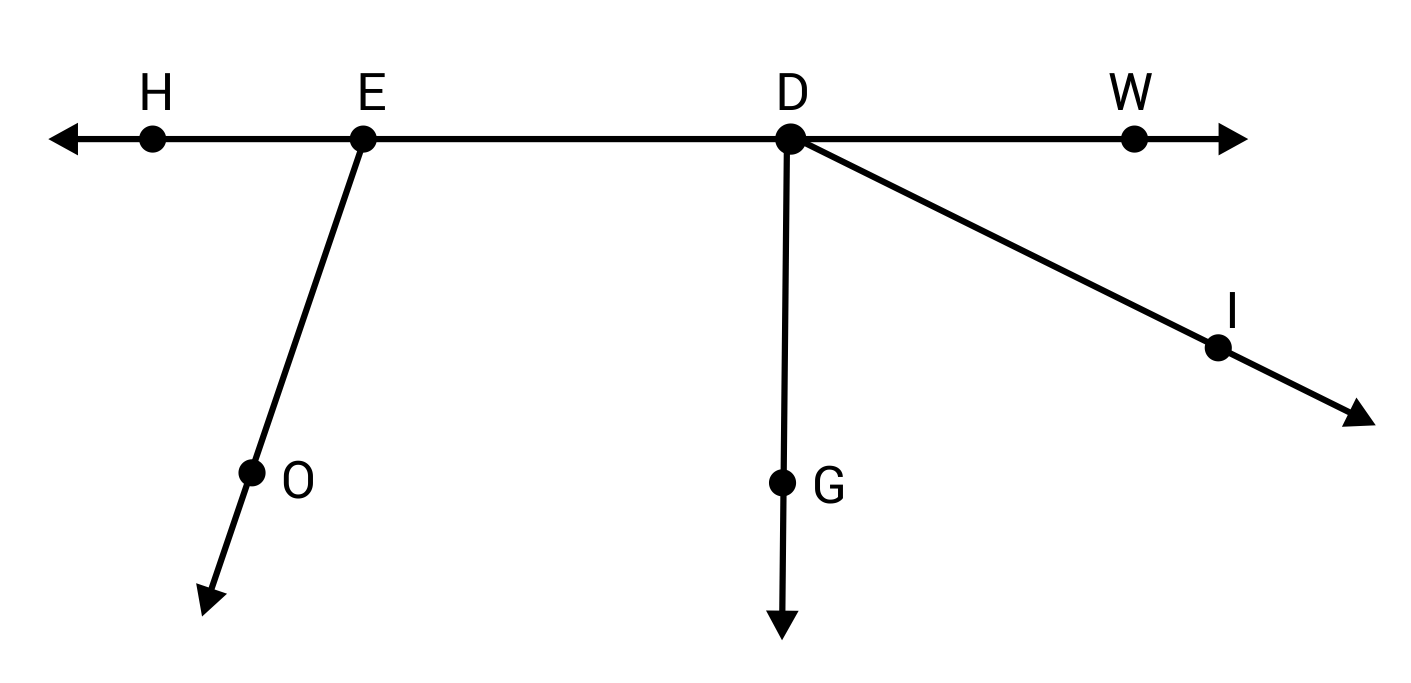
D is the correct answer because ∠DEO and ∠WDI are not adjacent angles. They do not share a side or a vertex. Choices A, B, and C are incorrect because these answer options list angle pairs with common sides and a common vertex.
Keisha and James are looking at a map of city streets and notice a lot of adjacent angles. James draws the image shown to illustrate the angles they find. Keisha points out that ∠AOE and ∠COD are adjacent because they share a vertex and one side. James disagrees. He says that these angles do not have a common side. Who is correct, and why?
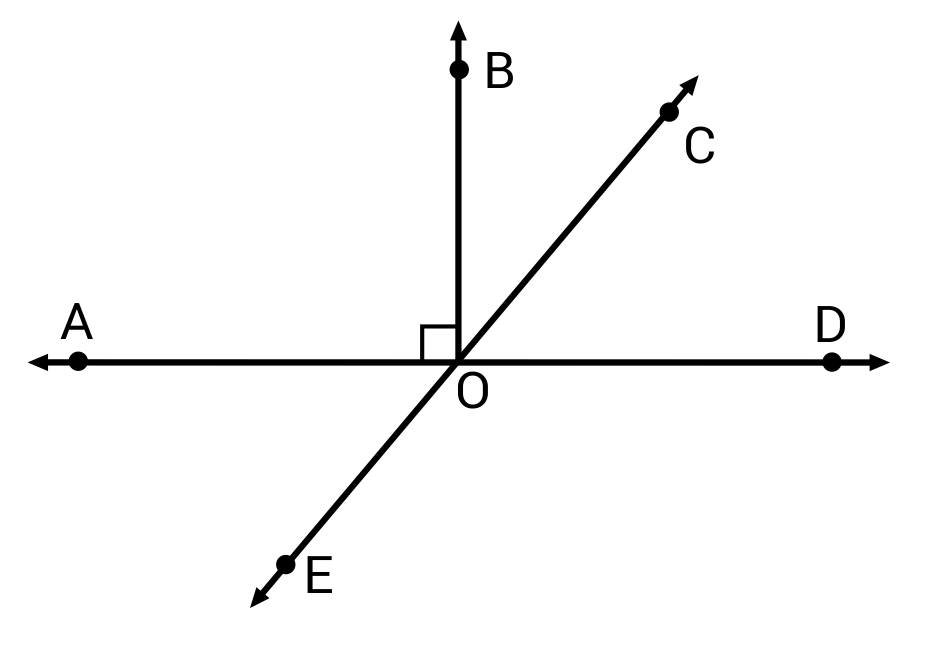
A is the correct answer because ∠AOE and ∠COD share a vertex at point O but they do not share a side. Therefore, James is correct. B is incorrect because line AD is not a line in ∠AOE or ∠COD. C is incorrect because ∠AOE and ∠COD share a vertex at point O. D is incorrect because although Keisha is incorrect, the justification given in this answer option is wrong. ∠AOE is shown on the map.