
Hi, and welcome to this video on finding the area and perimeter of a trapezoid!
What is a Trapezoid?
A trapezoid is a four-sided polygon, or “quadrilateral,” that has at least one set of parallel sides. There are two types of sides in a trapezoid: legs and bases. A trapezoid has two legs and two bases.
We can tell which sides are the bases because they are parallel to each other.
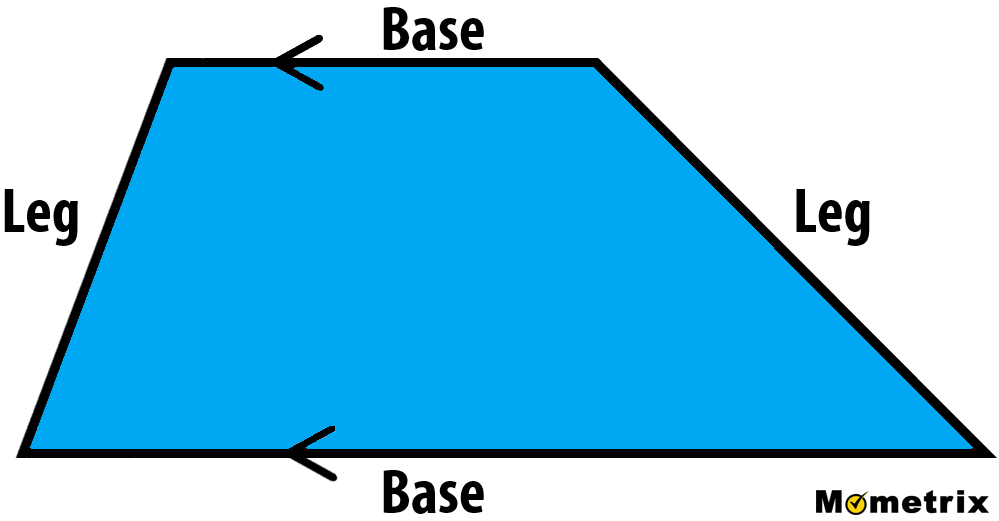
Here, we can see the top and bottom are parallel because of the matching arrows on those sides.
How to Find the Perimeter of a Trapezoid
When we know the lengths of the legs and the lengths of the bases we can find the perimeter of the trapezoid. The perimeter is the distance around an object. For instance, if we wanted to build a fence around a trapezoid-shaped yard, we’d need to know the perimeter of the yard to know how much fencing to buy.
Trapezoid Perimeter Formula
For a trapezoid, the formula for perimeter is \(P=b_1+b_2+l_1+l_2\).
We don’t need to remember this formula though, because just like with every other type of polygon, it’s just a fancy way of saying add all of the sides together!
Let’s go ahead and find the perimeter of this trapezoid:
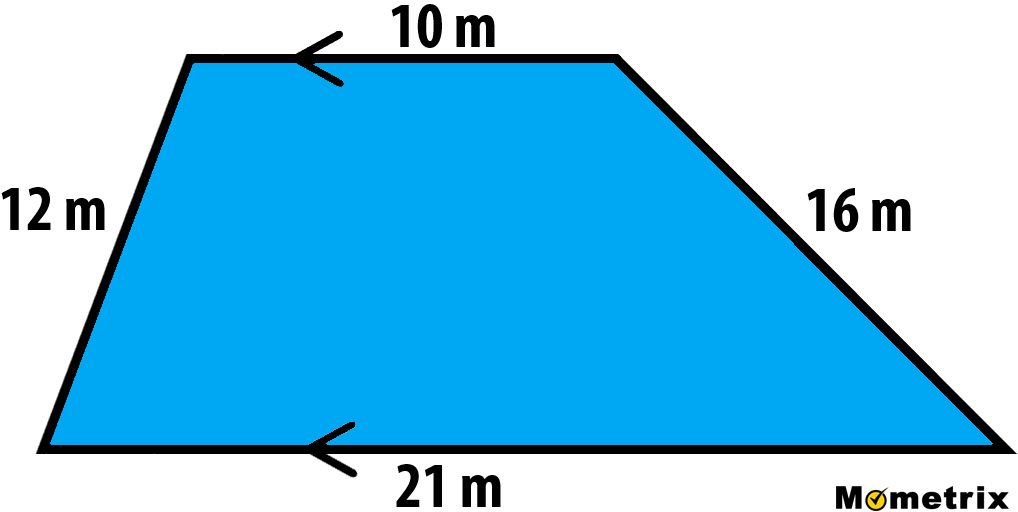
That’s all there is to it! Let’s move on to area.
How to Find the Area of a Trapezoid
Here’s a trapezoid on some graph paper:
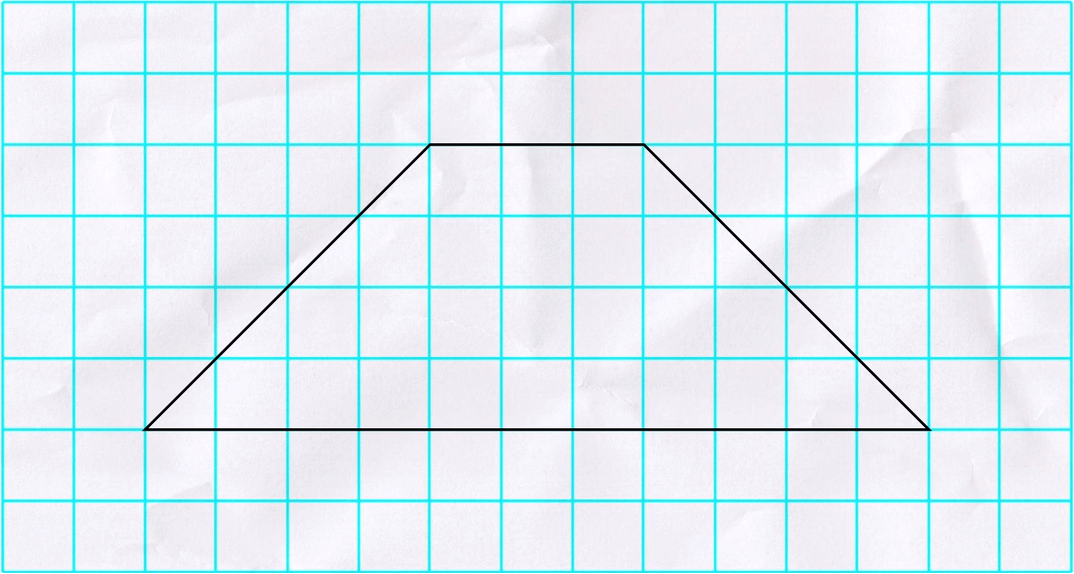
Remember that area is a measure of how many square units will fit inside a shape. How many squares are inside our trapezoid?

There are 24 full squares plus eight half squares, which means the area of the trapezoid is 28 square units. But what if we don’t have graph paper or a conveniently sized trapezoid? That’s why we need a formula!
Trapezoid Area Formula
The formula for finding the area of a trapezoid is \(A=h(\frac{b_1+b_2}{2})\).
Note that dividing the sum of the bases by two is the average of those lengths. Because our sample problem is on a graph, we can see that the top base, which we’ll call base 1, is three units long. Our bottom base, base 2, is 11 units longs. The height of the trapezoid, which is the distance between the bases, is four units:
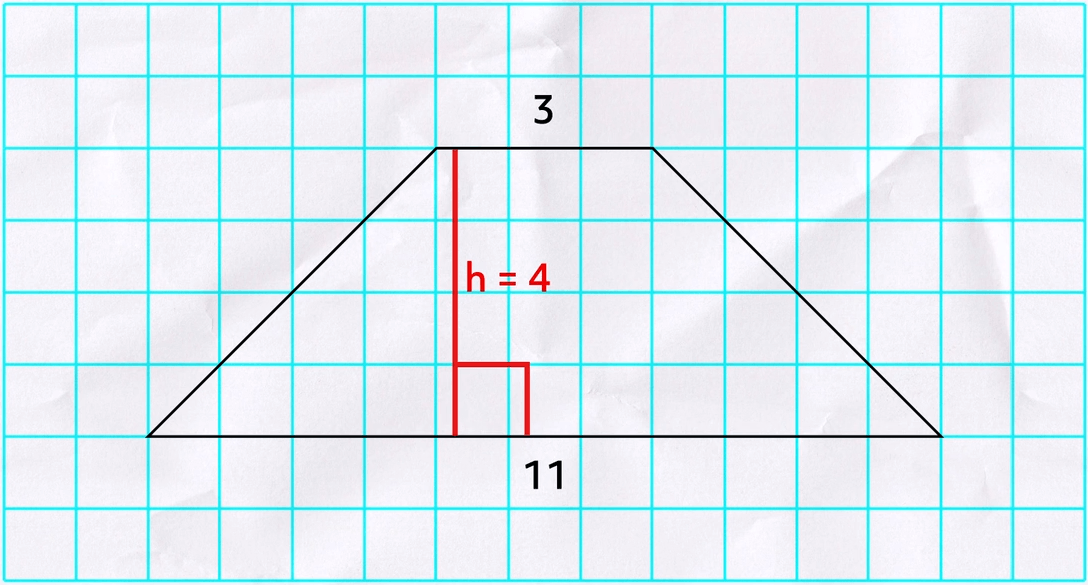
For area, we don’t need the measurements of the two legs, just the two bases and the height, which can also be called the altitude. Since we have all three we can plug them into our formula:
That’s the same answer we got when we counted!
Let’s try another one:
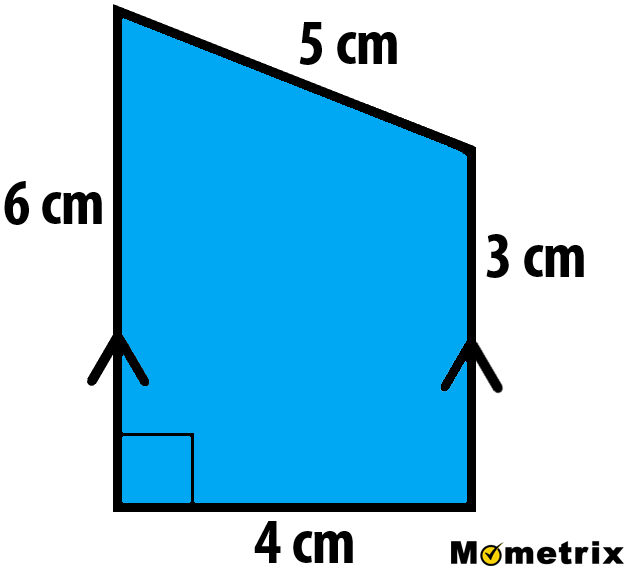
Okay, it looks a bit different than the trapezoid we just did. But we can tell it’s a trapezoid because it has one set of parallel sides. We can use the formula, so now we just need to figure out which numbers go where. The parallel sides are the bases so we can set base one as 6 centimeters and base two as 3 centimeters. There’s no dashed or colored line inside the trapezoid connecting the bases that would clearly be the height, but the bottom side is connecting the bases and is perpendicular to them, as we can tell by the right angle symbol. So 4 centimeters is the height, even though it’s sideways! Let’s plug it all in:
This formula also works to find the area of parallelograms too. That’s because all parallelograms are trapezoids since they have at least one set of parallel sides. In fact, all parallelograms have two sets.
That’s about all there is to finding the perimeter and area of trapezoids.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you find the area of a trapezoid?
A
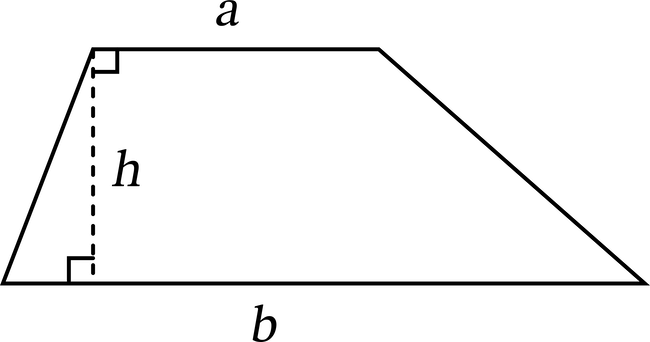
Each of the two parallel sides of a trapezoid is a base. The distance between the bases (measured perpendicular to each) is the height. To find the area of a trapezoid, we multiply the average length of the two bases by the height. In symbols, if the lengths of the bases are \(a\) and \(b\) and the height is \(h\) (see diagram), then the area, \(A\), of the trapezoid is \(A=\frac{(a+b)}{2}h\), which we can also write as \(A=\frac{1}{2}(a+b)h\).
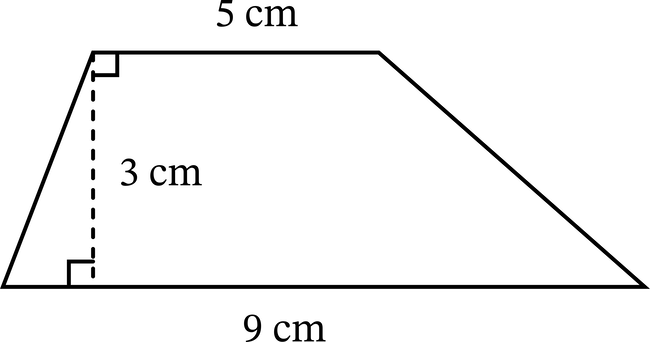
For example, the trapezoid in the diagram with bases of length 5 cm and 9 cm and with height 3 cm has an area of \(A=\frac{5+9}{2}\cdot3=\frac{14}{2}\cdot3=7\cdot3\)\(=21\text{ square centimeters}\), which we may also write as \(21\text{ cm}^2\).
Q
Why does the area formula for a trapezoid work?
A
The area formula for a trapezoid works because it comes from the formula for the area of a parallelogram. The trapezoid below (with solid sides) has bases of length \(a\) and \(b\) and height \(h\). Suppose we make a copy of it, rotate it halfway around, and place it adjoining the original trapezoid so that legs (non-parallel sides) of the same length coincide (the shaded trapezoid with dashed sides). Together these figures form a parallelogram with a base of length \(a+b\) and height \(h\). By the standard formula, the area of this parallelogram is \(\text{area}=\text{base}×\text{height}=(a+b)h\). The area of the original trapezoid is half of this, namely \(\frac{1}{2}(a+b)h\), or, equivalently, \(\frac{(a+b)}{2}h\). This same procedure works for every trapezoid.

Q
What units do you use for the area of a trapezoid?
A
We measure the area of a trapezoid, like all areas, in square units–square feet, square inches, square meters, etc.—which are sometimes written \(\text{ft}^2\), \(\text{in}^2\), \(\text{m}^2\), etc. Usually, we use the square of the unit used to measure the bases and height of the trapezoid. For instance, if we measure the bases and height in centimeters, we usually give the area in square centimeters.
Q
How do you find the perimeter of a trapezoid?
A
The perimeter of a figure is the distance around it. We find the perimeter of a trapezoid by adding up the lengths of its four sides.
Q
How do you find the perimeter of a trapezoid using the Pythagorean theorem?
A
If we do not know the lengths of all four sides of a trapezoid, sometimes we have enough other information to find the lengths of the missing sides using the Pythagorean theorem. For example, in the trapezoid in the diagram, the bases are 2 cm and 9 cm, the height is 4 cm, and the longer base sticks out past the shorter base by 3 cm on the left and 4 cm on the right. This makes sides \(c\) and \(d\) hypotenuses of right triangles with sides whose lengths we know. By the Pythagorean theorem, \(c^2=3^2+4^2=9+16=25\), so \(c=\sqrt{25}=5\text{ cm}\). Similarly, \(d^2=4^2+4^2=16+16=32\), so \(d=\sqrt{32}=\sqrt{16\cdot2}\)\(=\sqrt{16}\cdot \sqrt{2}\)\(=4\sqrt{2}≈5.7\text{ cm}\). Now we can find the perimeter, \(P\), of the trapezoid by adding up the four sides: \(P=9+5+2+4\sqrt{2}\)\(=16+4\sqrt{2}≈16+5.7\)\(=21.7\text{ cm}\). This is one example of finding the perimeter of a trapezoid using the Pythagorean theorem.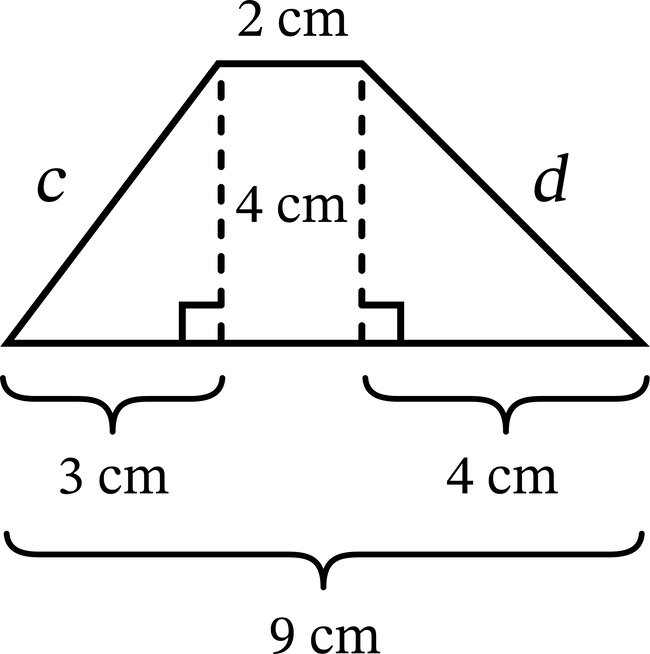
Q
How do you find the area of a trapezoid without the height?
A
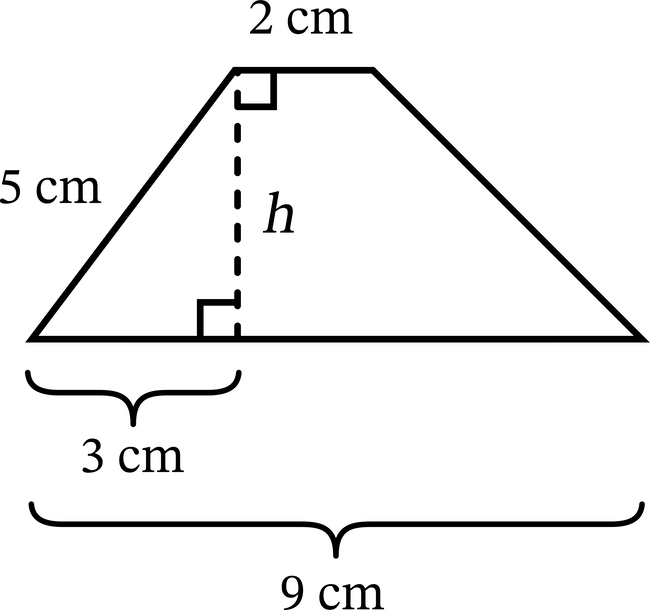
If we do not know the height of a trapezoid, sometimes we have enough other information to find the height using the Pythagorean theorem. For example, in the trapezoid in the diagram, the bases are 2 cm and 9 cm, the longer base sticks out 3 cm past the shorter base on the left, and the left leg (the non-parallel side) is 5 cm. This makes the dashed line a side of a right triangle whose hypotenuse and other side we know. By the Pythagorean theorem, \(h^2+3^2=5^2\) or \(h^2+9=25\). So, \(h^2=16\) and \(h=\sqrt{16}=4\text{ cm}\), which is the height of the trapezoid. Now we can apply the standard formula to find the area of this trapezoid: \(A=\frac{(a+b)}{2}h=\frac{(2+9)}{2}\times4\)\(=\frac{11}{2}\times4=\frac{11}{1}⋅2=22\text{ cm}^2\). This is an example of finding the area of a trapezoid without the height.
Area and Perimeter of a Trapezoid Practice Problems
What is the perimeter of this trapezoid?
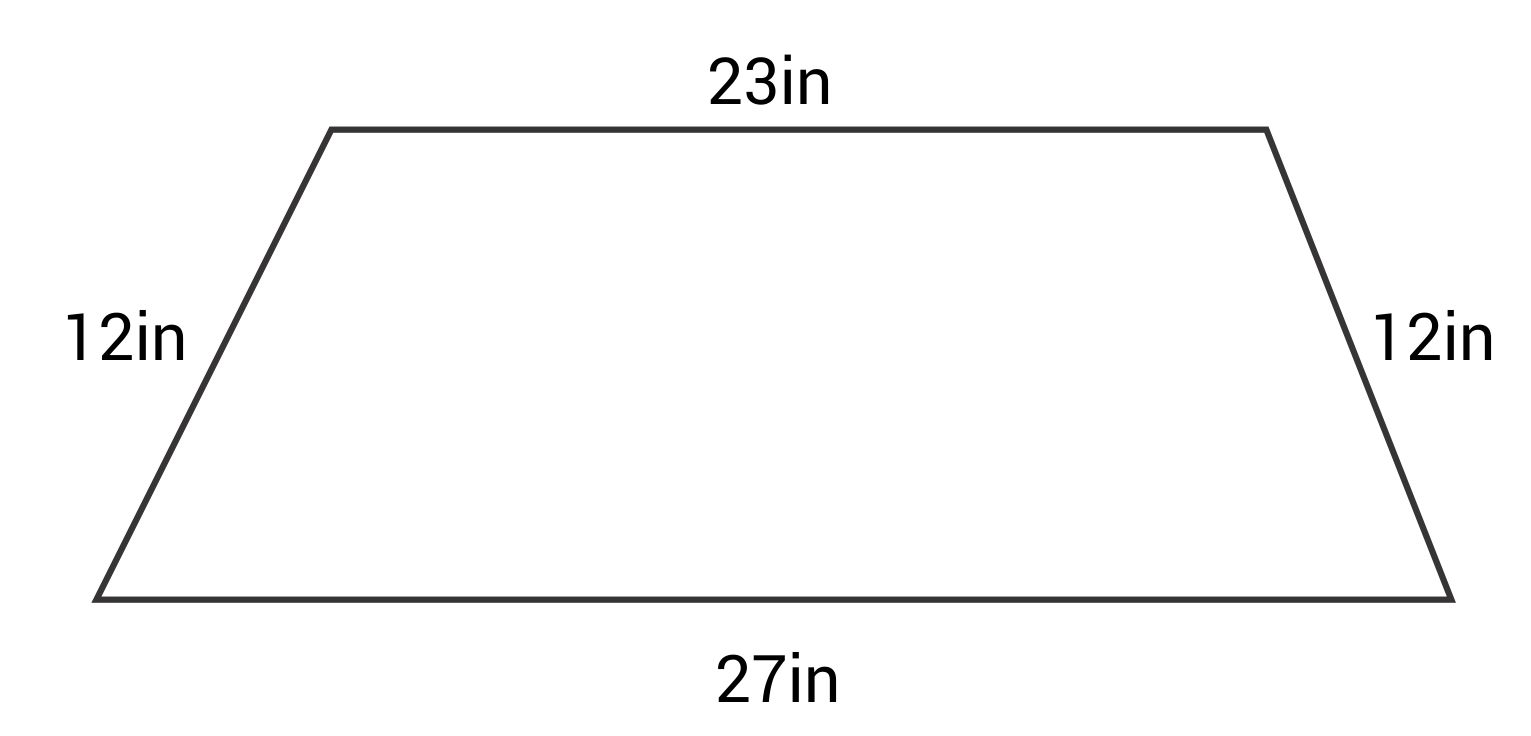
The correct answer is 74 in. To find the perimeter of a trapezoid, add all four side lengths together.
\(P=23+12+27+12=74\text{ in}\)
What is the area of this trapezoid?
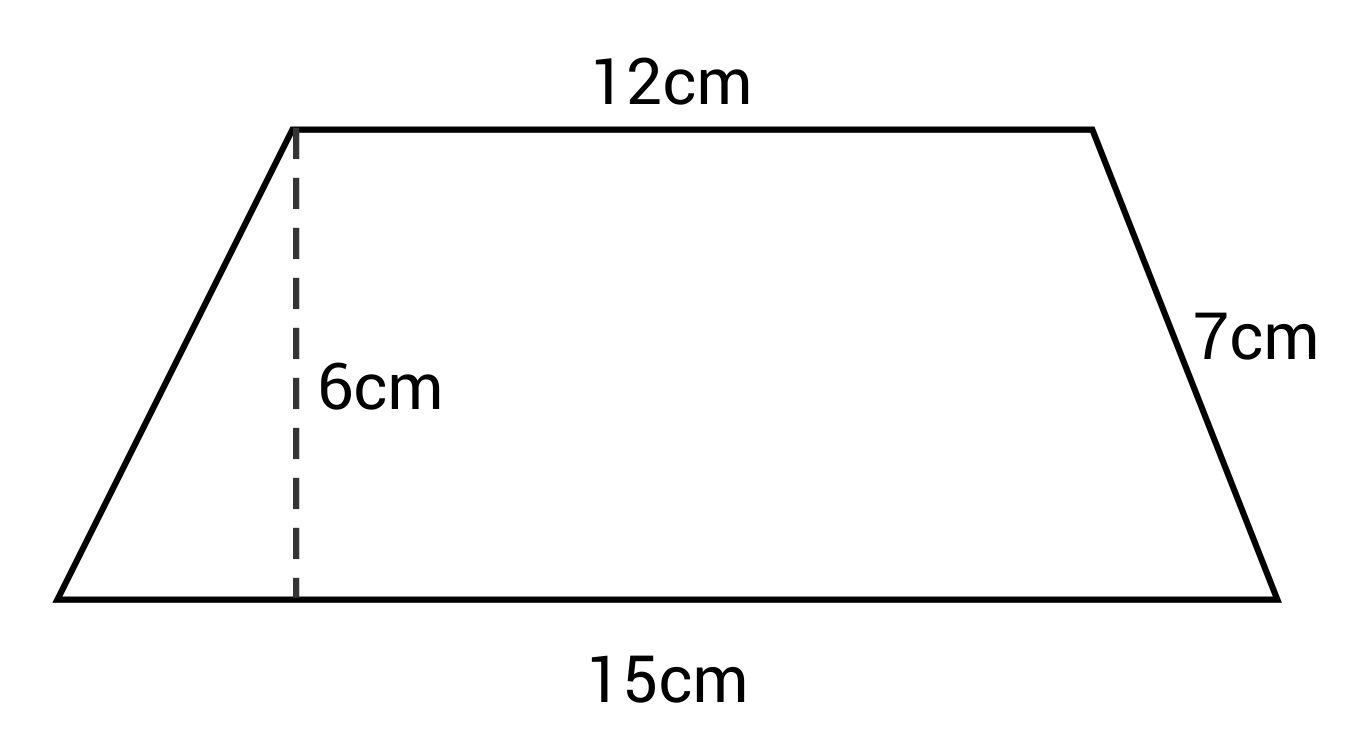
The correct answer is 81 cm2. The formula for area of a trapezoid is:
\(A=\frac{1}{2}(b_1+b_2)h\)
The length base 1 is 12 cm. The length of base 2 is 15 cm. The length of the height is 6 cm.
\(A=\frac{1}{2}(12+15)(6)\)\(=\frac{1}{2}(27)(6)=81\text{ cm}^2\)
What is the perimeter of this trapezoid?
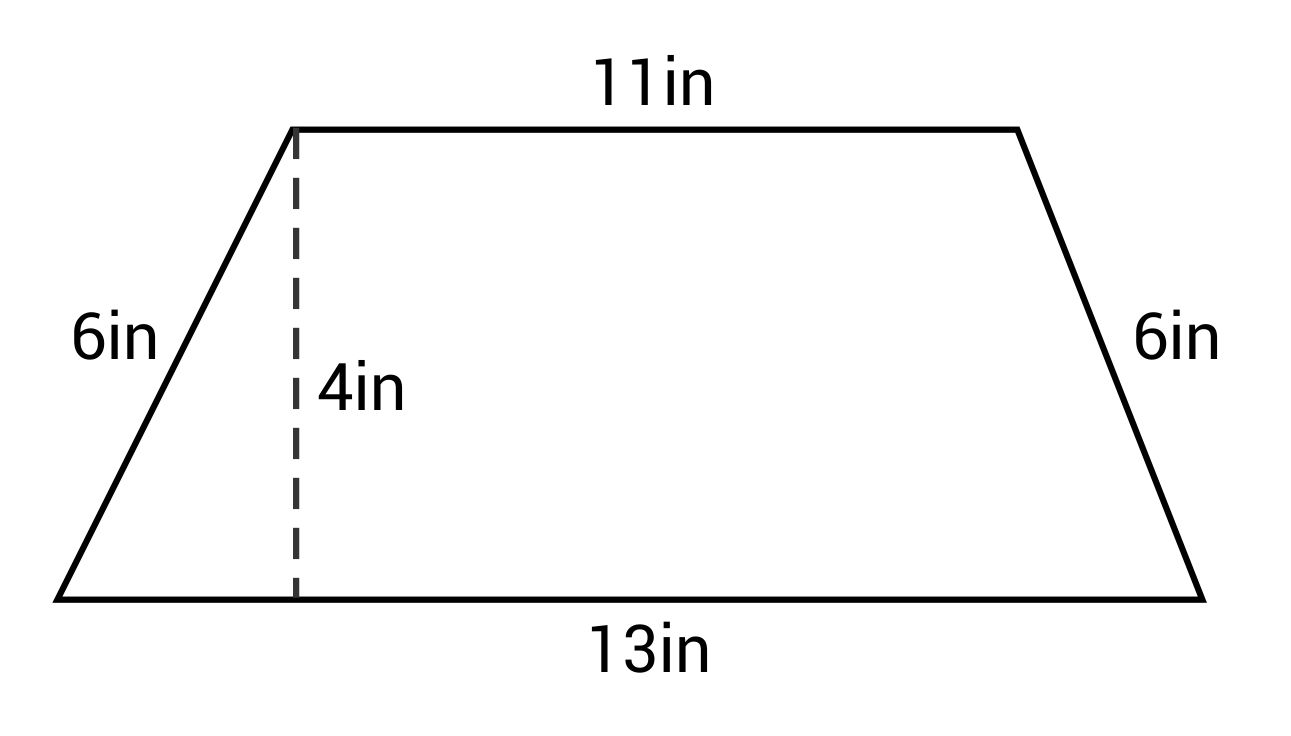
The correct answer is 36 in. Find the perimeter of the trapezoid by adding the lengths of all four sides together.
\(P=11+6+13+6=36\text{ in}\)
What is the area of this trapezoid?
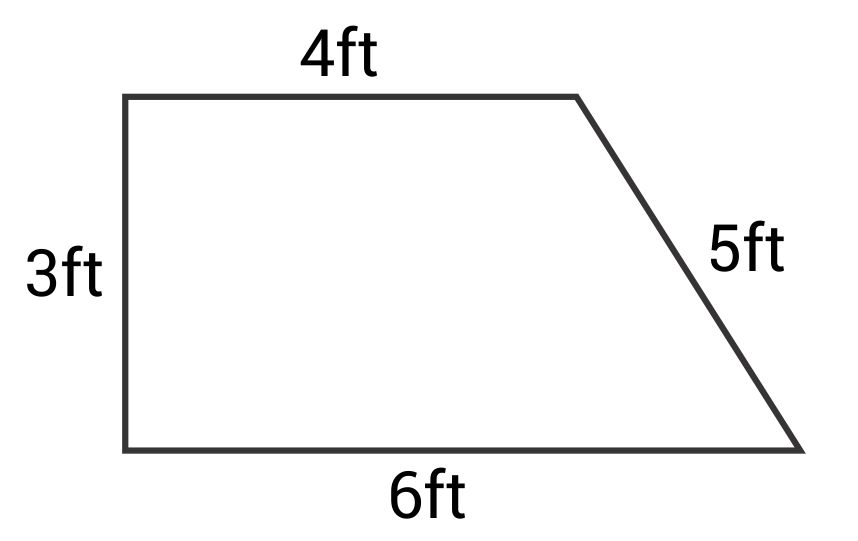
The correct answer is 15 ft2. The formula for area of a trapezoid is:
\(A=\frac{1}{2}(b_1+b_2)h\)
The length of base 1 is 4 ft. The length of base 2 is 6 ft. The length of the height is 3 ft.
\(A=\frac{1}{2}(4+6)(3)=\frac{1}{2}(10)(3)\)\(=15\text{ ft}^2\)
What is the perimeter of this trapezoid?
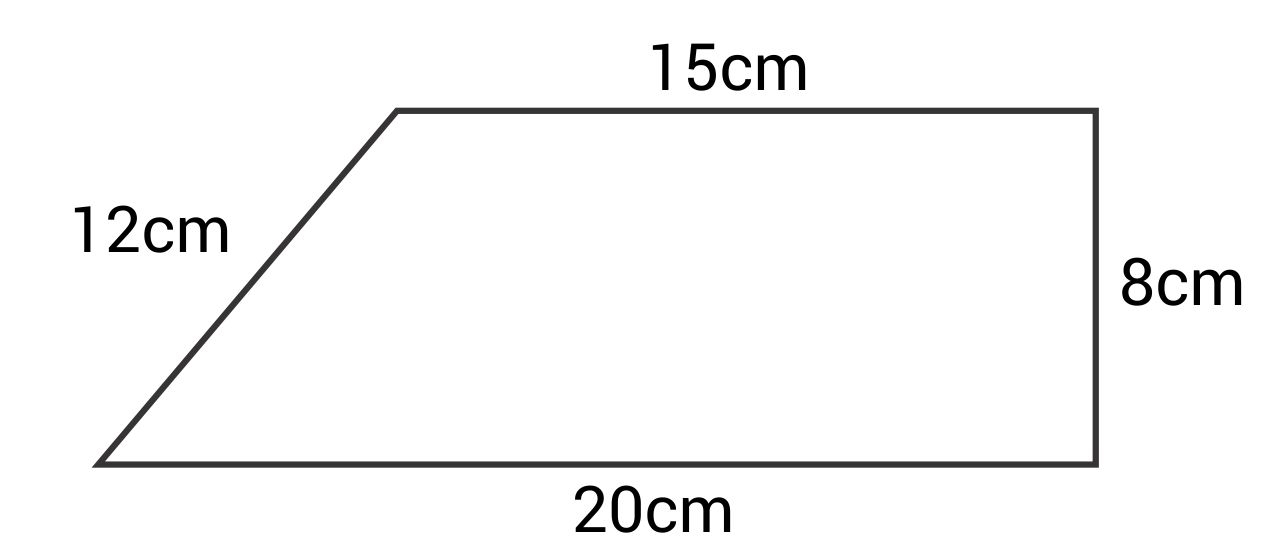
The correct answer is 55 cm. To find the perimeter of a trapezoid, add the lengths of all four sides together.
\(P=15+8+20+12=55\text{ cm}\)