
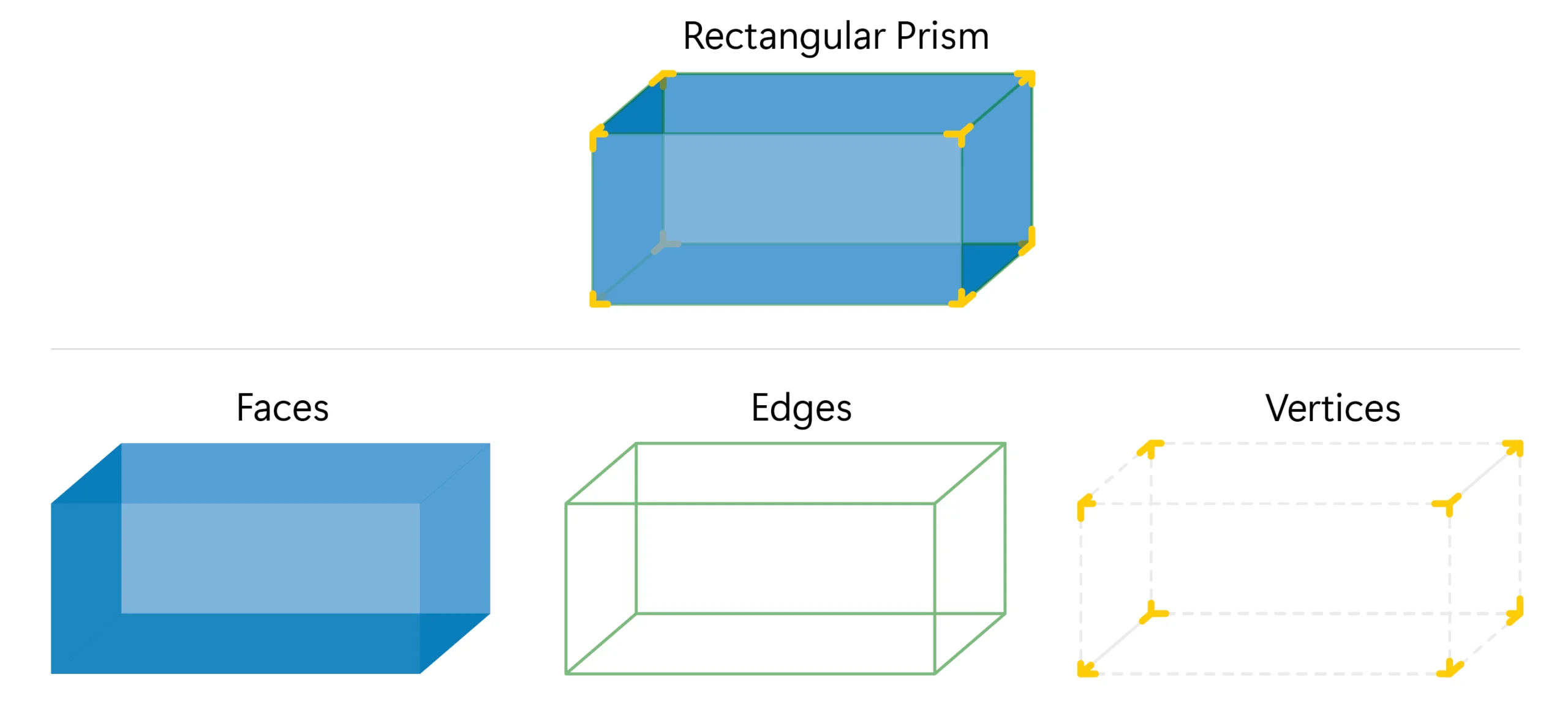
Hello! Today we’re going to examine the most common of 3D figures, the rectangular prism, also known as a rectangular solid. Like with most 3D figures, we can calculate the volume and the surface area by using relatively simple formulas. But before we do that, we need to define a few terms.
A rectangular prism, or rectangular solid, is a six-sided object where each side, also called a face, is a rectangle. It has twelve edges and eight vertices and all of its angles are right angles.
An important measure of a rectangular prism is the volume. The volume of a prism or any other 3D object is a measure of how much space it takes up. We measure this in cubic units, such as cubic inches or cubic centimeters. It’s easy to picture this with a rectangular prism. Imagine that we have a bunch of little cubes that are 1 centimeter tall, 1 centimeter wide, and 1 centimeter long. Each one of these cubes is 1 cubic centimeter, which can also be written like this \(1\text{ cm}^3\). This is our unit of measure. Notice that it is in cubic units. Volume is a 3-dimensional measure so it’s always in cubic units.
Now let’s build a rectangular prism out of the little centimeter cubes. We’ll start with the lowest level and arrange them in a \(5\times 3\) rectangle. At this point, we’ve used 15 cubes to make our shape, and we have successfully created a rectangular prism.
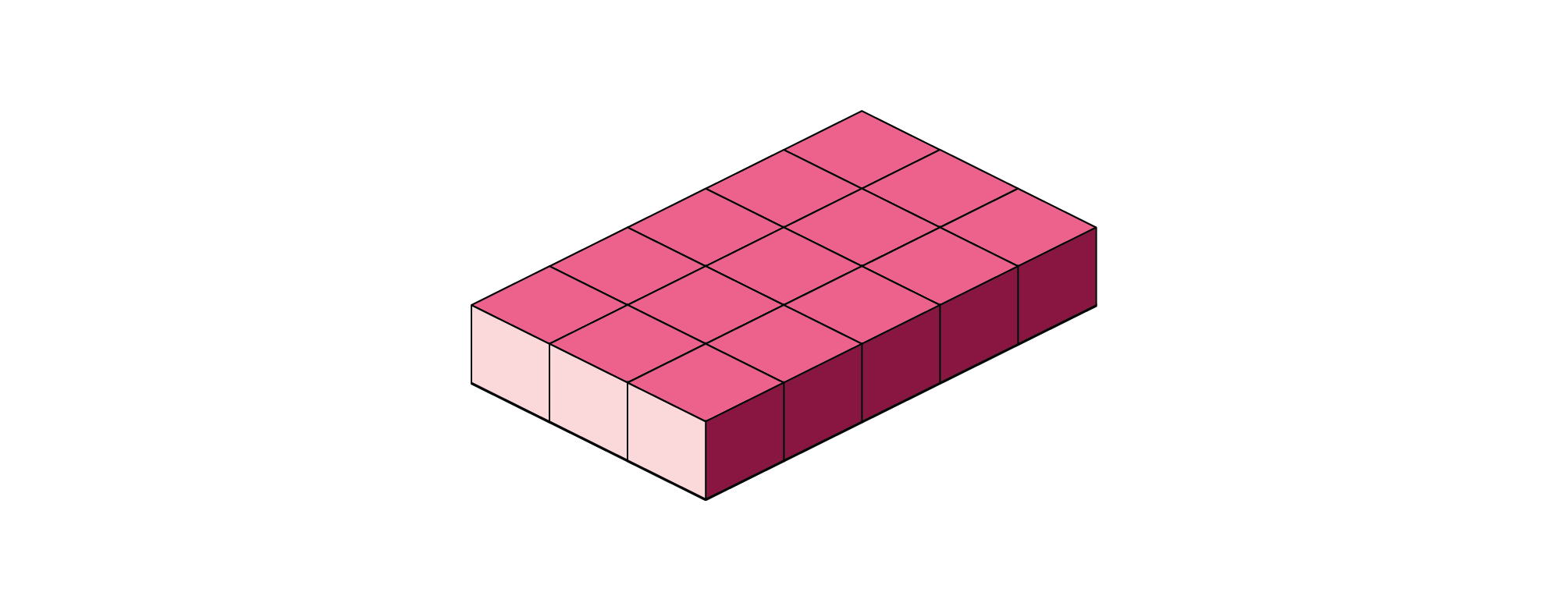
But we can also stack the cubes to make it a little taller. If we place another layer of cubes on top of the first layer, we’ll have a \(5\times{3}\times{2}\) rectangular prism. And since we used 15 more little cubes to make the second layer, we’re up to 30 cubes altogether. So the volume of our prism is \(30\times \text{ cm}^3\).
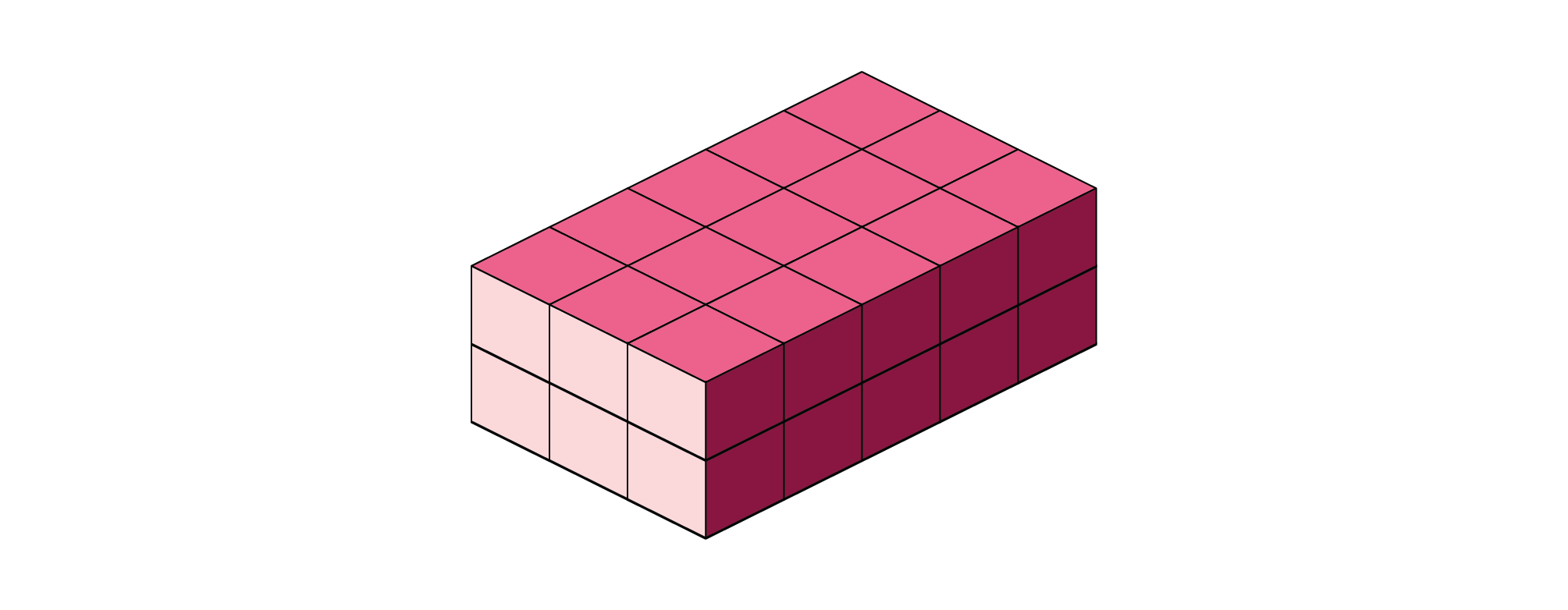
Notice that if we multiply the dimensions of our \(5\times{3}\times{2}\) cube, we get our volume! That’s because the formula for the volume of a rectangular prism is the product of the dimensions:
So in this case, our volume \(V=5\times{3}\times{2}=30\). But let’s not forget our units! Technically our prism measures \(5\text{ cm}\times{3}\text{ cm}\times{2\text{ cm}}. 5\times{3}\times{2}=30\) and \(\text{cm} \times \text{cm} \times \text{cm}=\text{cm}^3\)
An example of a real-world volume problem is if we needed to pour a foundation for a rectangular building – we need to measure the area of each side of the building to find out how much concrete we need to prepare. So if we had to pour a foundation that is \(42.5\text{ m long}\times{20\text{ m wide}}\times{0.4\text{ m deep}}\) (this is height), we can use those dimensions to find the volume of our foundation by plugging that into our formula:
Now let’s work on finding the surface area. Surface area has “area” in the name because it really is a measure of area and therefore is a 2-dimensional measure. Its units are therefore square units, like \(\text{cm}^2\). It’s well-named because we’re literally finding the area of the outer surface of the object. So all we need to do is find the area of each face, or side, of our rectangular prism and then add all the sides together. If we take a look at the prism we built from our little centimeter cubes, we can see the squares on the faces. Each one of these squares is a square centimeter.
We can see three of the six faces from this angle. The top face has 15 squares. The left face has 6, and the right face has 10. If we add those up, we have 31 square centimeters that we can see. But since this is a rectangular prism, we know that the sides we can’t see are the same size as the ones we can. The bottom is the same size as the top. The back left is the same size as the front right, and the back right is the same size as the front left. That means that the area of the sides we can’t see also totals 31 square centimeters. Therefore our total surface area is \(31\text{ cm}^2+31\text{ cm}^2\) for a total of \(62\text{ cm}^2\).
This problem lets us see the square centimeters, but most surface area problems won’t show us the squares. We’ll just know the dimensions of the rectangular prism, like this:
Here we can see our prism is 10 meters long by 5 meters wide by 4 meters high. The corresponding edges on the opposite sides will be the same since this is a rectangular prism. The find the surface area, I can use the surface area formula for rectangular prisms:
This formula will give us the surface area if we plug in our length, width, and height.
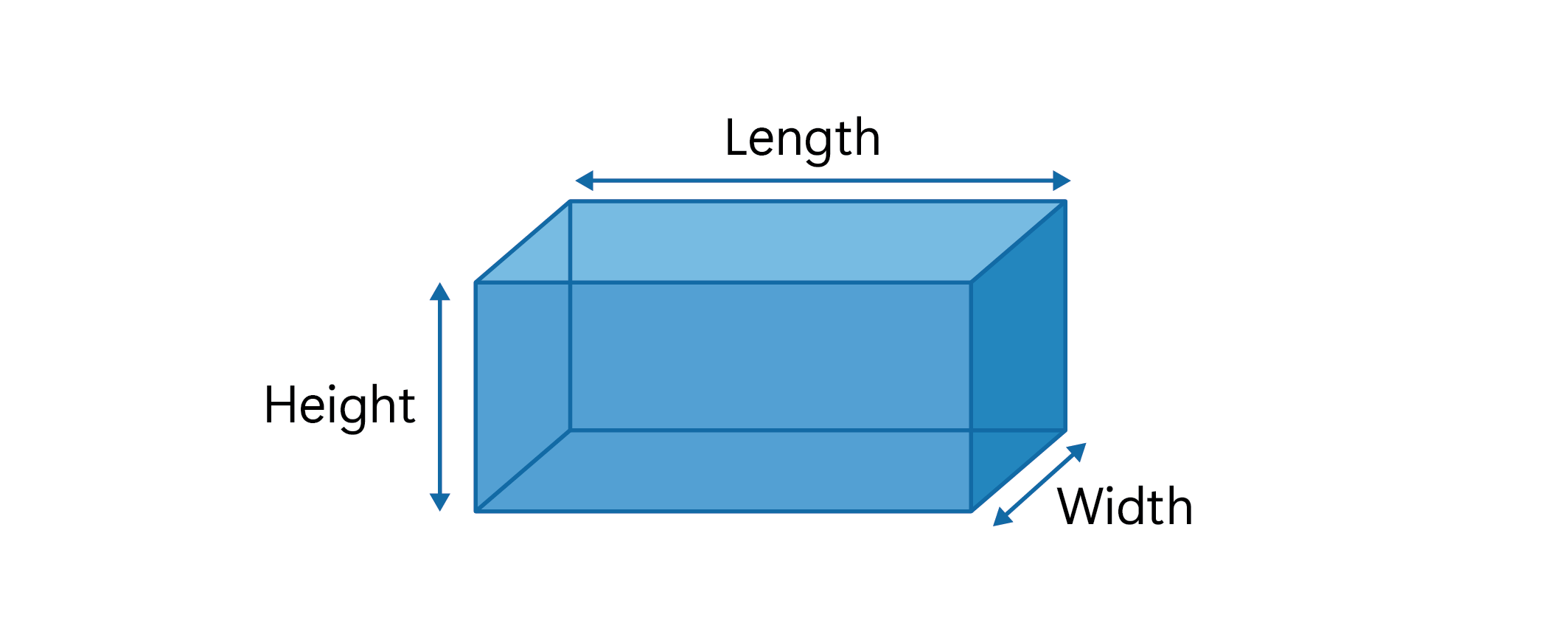
Don’t be confused about which sides are the length, width, and height. Depending on how the prism is oriented on the page, it might appear the 10 m is the length but it really could be the width or the height. It doesn’t matter! But for our purposes, let’s say 10 m is the length, and 5 m is the width, and 4 m is the height. When we substitute all that in it looks like this:
Notice that we left the units in when we substituted. Now when we evaluate each term, we get that the surface area is equal to:
Notice that our units ended up being square units, which is what we need for the surface area. Finally, we just add the terms together to get that our surface area is equal to 220 square meters.
Not too difficult, but it’s worth the time to take a moment to look at what that formula is really doing:
The first term, \(2lw\), is double the length times the width. This is calculating the area of the bottom and the top of the rectangular prism. The 2 is there to double the area of either one of the sides. The middle term, \(2lh\), is double the length times the height. In other words, the front and back sides of the prism. The final term, \(2wh\), is double the width times the height. In other words, the left and right sides of the prism.
So the formula is simply finding the area of all 6 sides of the prism 2 at a time. That means that if we ever forget the formula, we can simply find the area of each side individually and add them all up. It takes a bit longer but it totally works.
I hope this video on the surface area and volume of rectangular prisms was helpful. Thanks for watching, and happy studying!
For more help, check out our rectangular prism calculator!
Volume and Surface Area of a Rectangular Prism Practice Questions
Determine the surface area of the rectangular prism.
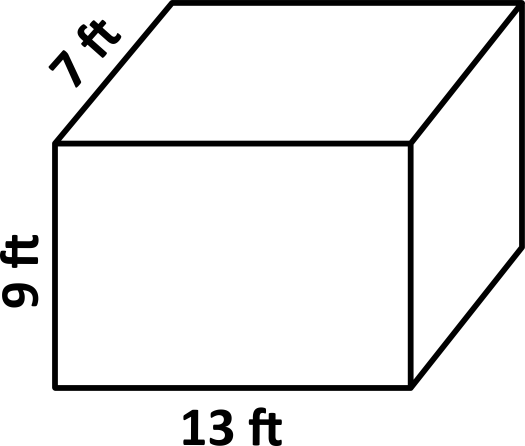
Rectangular prisms have 6 faces. Add the areas of the 6 faces in order to calculate the surface area. This can be done by using the formula:
\(SA=2lw+2lh+2wh\)
Plug in 13 for \(l\), 7 for \(w\), and 9 for \(h\).
\(SA=2(13)(7)+2(13)(9)+2(7)(9)\)\(=182+234+126=542\text{ft}^2\)
Since we are calculating an area measurement, the units are squared.
Calculate the volume of the rectangular prism. Round the answer to the nearest whole number.
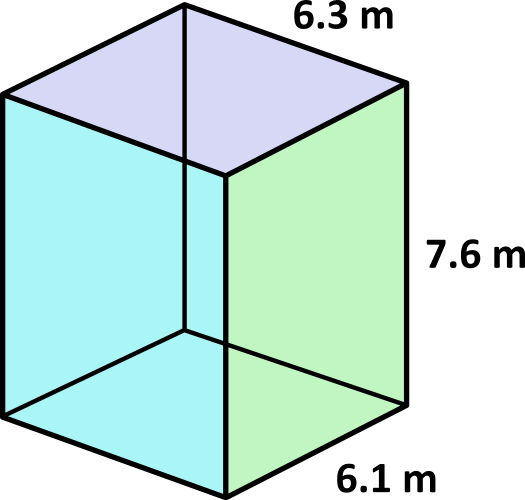
The volume of the rectangular prism is found using the formula \(V=lwh\). When the length, width, and height are multiplied, the formula becomes \(V=6.1\times6.3\times7.6\), which simplifies to 292.068. 292.068 rounded to the nearest whole number is \(292\text{ m}^3\).
Find the volume and surface area of the rectangular prism.
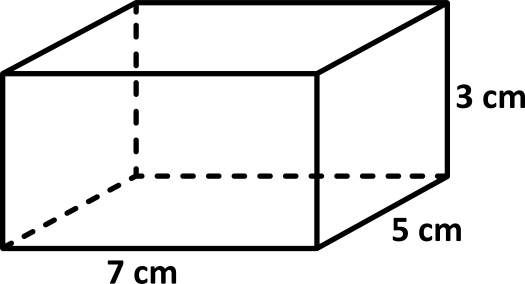
The surface area is calculated using the formula \(SA=2lw+2lh+2wh\).
Plug in 7 for \(l\), 5 for \(w\), and 3 for \(h\).
\(SA=2(7)(5)+2(7)(3)+2(5)(3)\)\(=70+42+30=142\text{ cm}^3\)
The volume is calculated by multiplying the length and width and height: \(V=lwh\). When the three dimensions are multiplied, the formula becomes \(V=7\times5\times3\), which simplifies to \(105\text{ cm}^3\).
Drea works for a company that installs swimming pools. What will the volume of the pool be if Drea fills the pool to the 4 meter mark?

The volume of the pool can be found by multiplying the length, width, and height: \(V=lwh\). If the pool is filled to the 4 meter mark, the formula becomes \(V=31.5\times9\times4\), which simplifies to \(V=1{,}134\text{ m}^3\).
George built a fish tank that connects two tanks with a middle section. This allows fish to swim back and forth between the chambers. How much water can the entire fish tank hold?
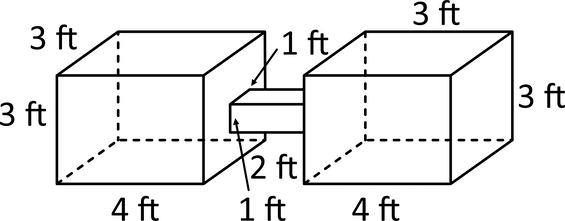
Volume is calculated as \(V=lwh\). The fish tank is made up of three rectangular prisms. Add the volumes of the three prisms.
Left Prism: \(V=lwh\) becomes \(V=4\times3\times3=36\text{ ft}^3\)
Right Prism: \(V=lwh\) becomes \(V=4\times3\times3=36\text{ ft}^3\)
Small Middle Prism: \(V=lwh\) becomes \(V=2\times1\times1=2\text{ ft}^3\)
The sum of the volumes of all three prisms is \(36\text{ ft}^3+36\text{ ft}^3+2\text{ ft}^3=74\text{ ft}^3\).