Where is the center of a triangle? How do you find it? It’s not as easy as finding the center of a circle or a rectangle and for a very good reason—there are as many as four different centers to a triangle, depending on how we try to find it! They are the incenter, centroid, circumcenter, and orthocenter.
Today, we’ll look at how to find each one.
Incenter
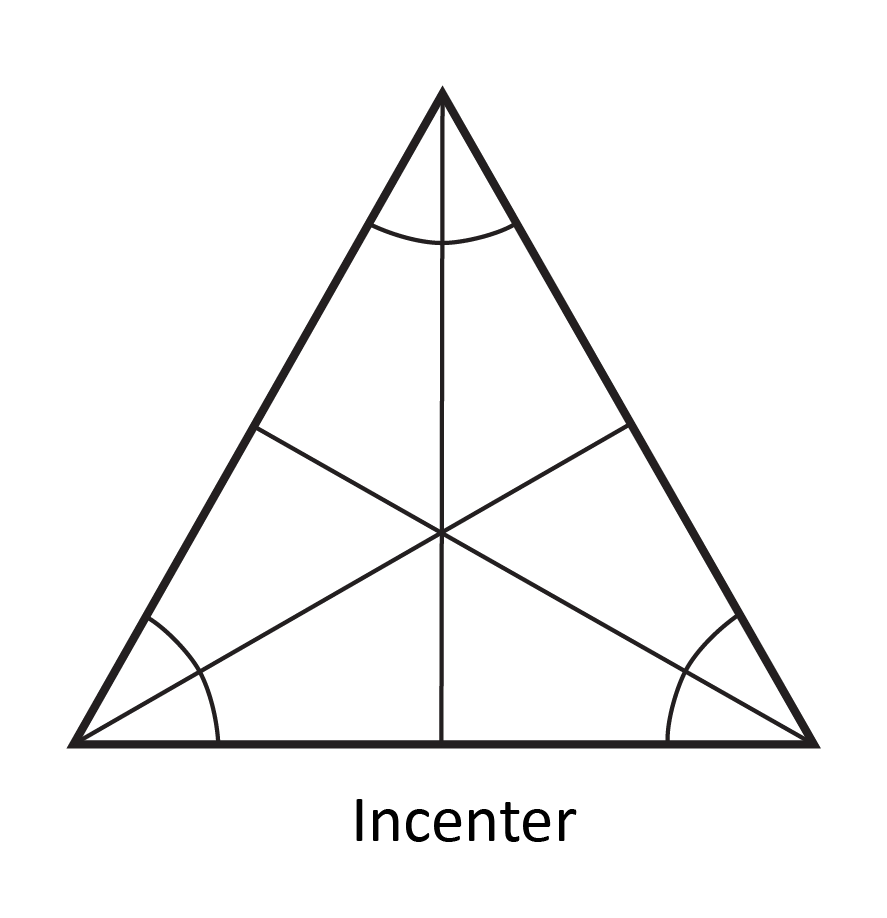
Let’s start with the incenter. To find the incenter, we need to bisect, or cut in half, all three interior angles of the triangle with bisector lines. Let’s take a look at a triangle with the angle measures given.
The angle on the left is 50 degrees, so we’ll draw a line through it such that it’s broken into two 25-degree angles. We’ll do the same for the 60-degree angle on the right, yielding two 30-degree angles and the 70-degree angle on the top, creating two 35-degree angles, like this:
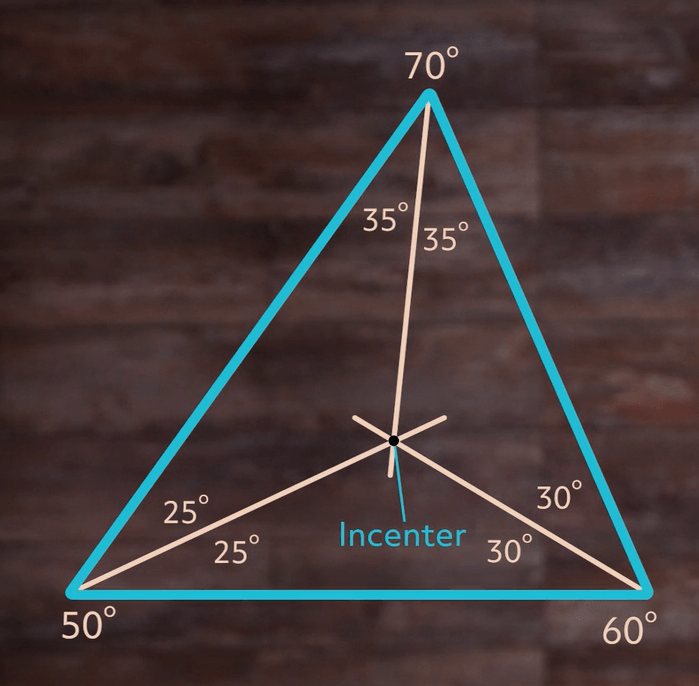
The point where the three angle bisector lines meet is the incenter.
Centroid
But what if we don’t cut the angles in half, but instead draw a line between each vertex and the midpoint of the line segment on the other side of the triangle? Let’s take a look at another triangle but this time we can see the lengths of the sides instead of the angle measures.
Let’s start by drawing a line between the angle on the left in a way that will cut the opposite side in half. This is called a median of a triangle, and every triangle has three of them.
As we can see, the opposite side that measures 10 meters has been split into two five-meter segments by our median.
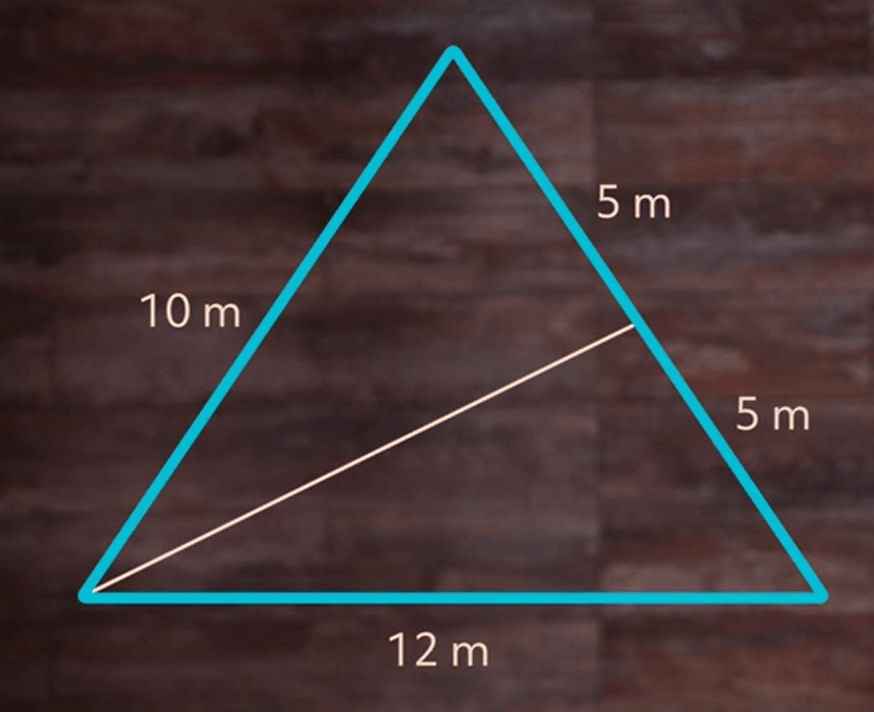
Now we need to draw the other two medians:
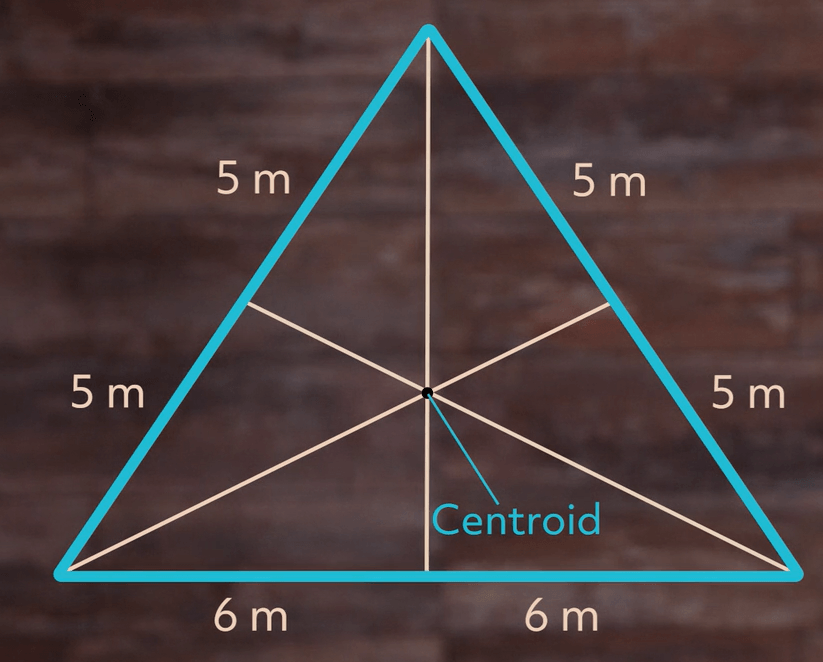
Centroid
Now that we’ve drawn all three medians, we can see where they intersect. This point is the centroid of the triangle and is our second type of triangle center.
Now that we’ve divided the angles in half to find the incenter and the sides in half to find the centroid, what other methods can we devise to find the other two centers? Remember, there’s four!
Let’s try a variation of the last one. We’ll start at the midpoint of each side again, but we’ll draw our lines at a 90-degree angle from the side, like this:
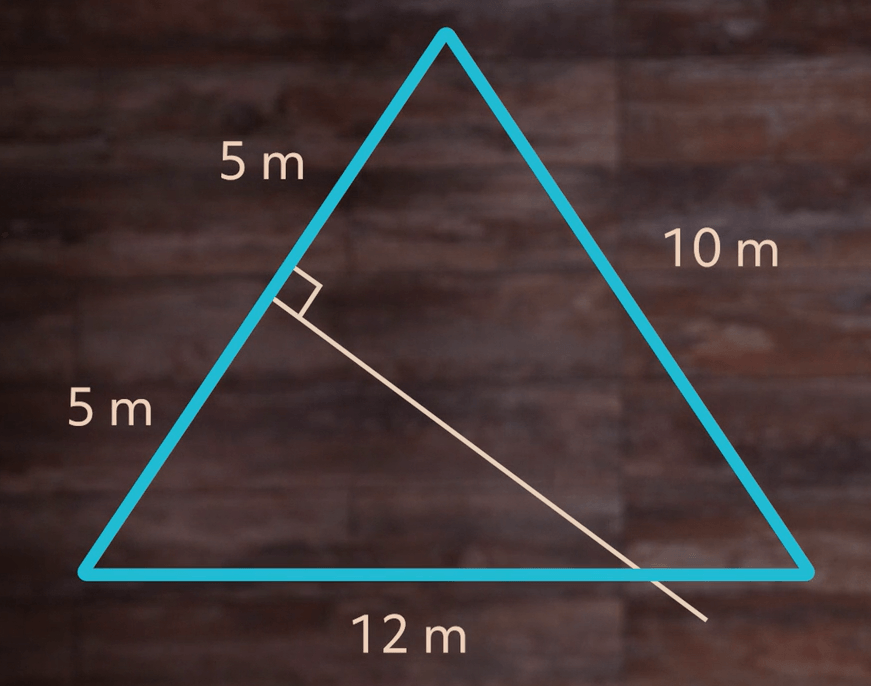
Notice that our line doesn’t end up at an angle, or as we sometimes say, a vertex. It cuts through another side. That’s totally fine! Let’s do the same thing with the other two sides:
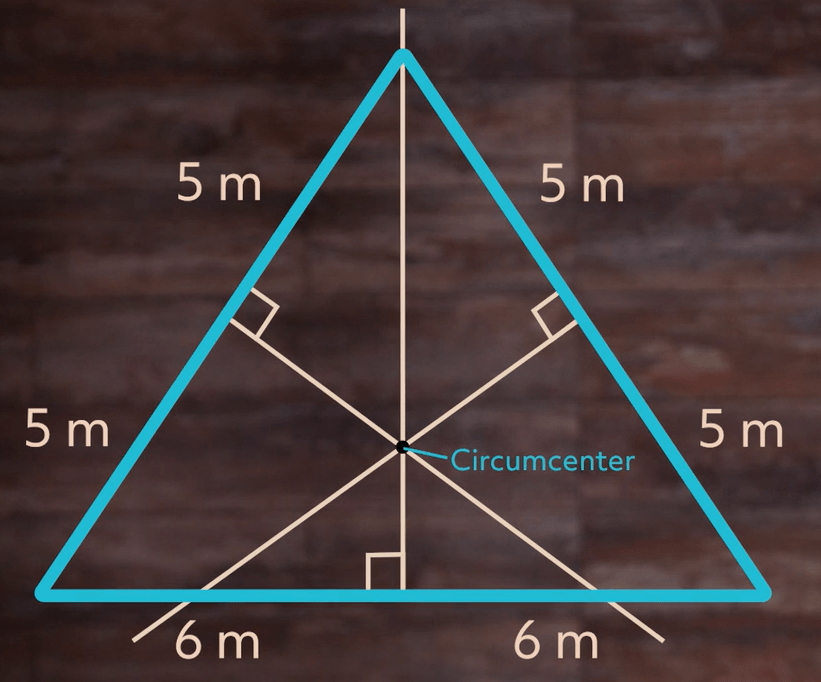
As we can see, all of our sides have perpendicular bisectors and all three of our bisectors meet at a point. This point is called the circumcenter of the triangle.
Orthocenter
Only one center left! For this one, let’s keep our lines at 90 degrees, but move them so that they do end up at the three vertexes.
When we do this, we’re finding the altitudes of a triangle. You might remember altitude because we need it to find the area of a triangle. If we draw the other two we should find that they all meet again at a single point:
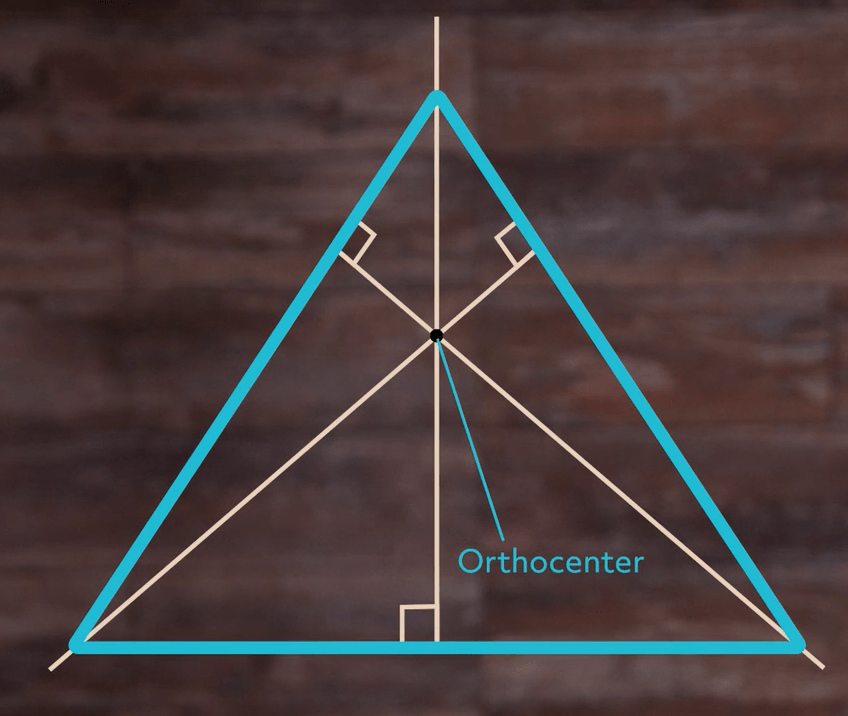
This is our fourth and final triangle center, and it’s called the orthocenter.
So, do you think you can remember them all? Pause this video and try to match up the name of the center with the method for finding it:
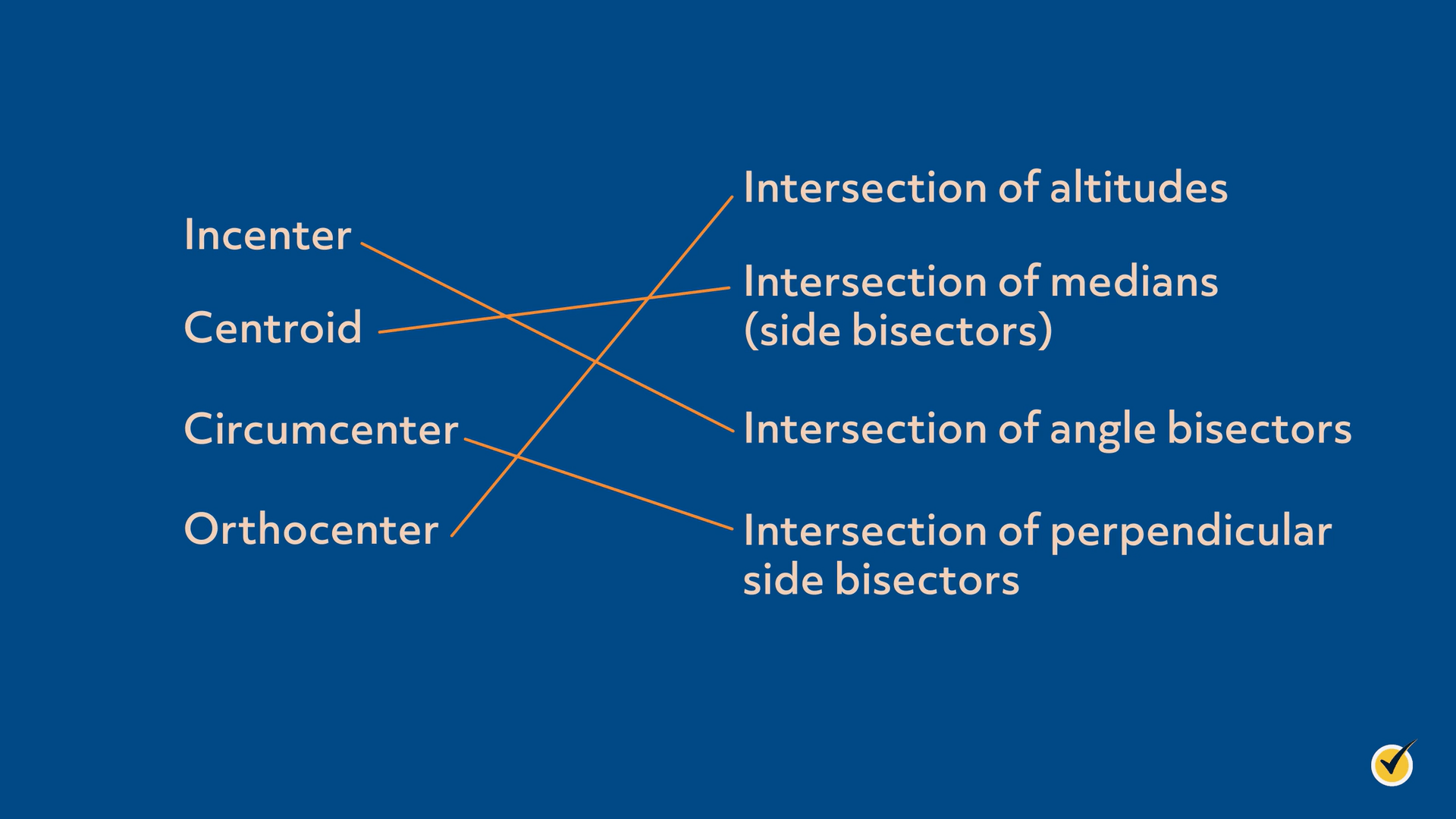
Thanks for watching, and happy studying!
Center of a Triangle Practice Questions
The center of the triangle below has been determined by constructing a line from each vertex to the opposite side in order to form a 90-degree angle with that side. This location is known as the ___________.
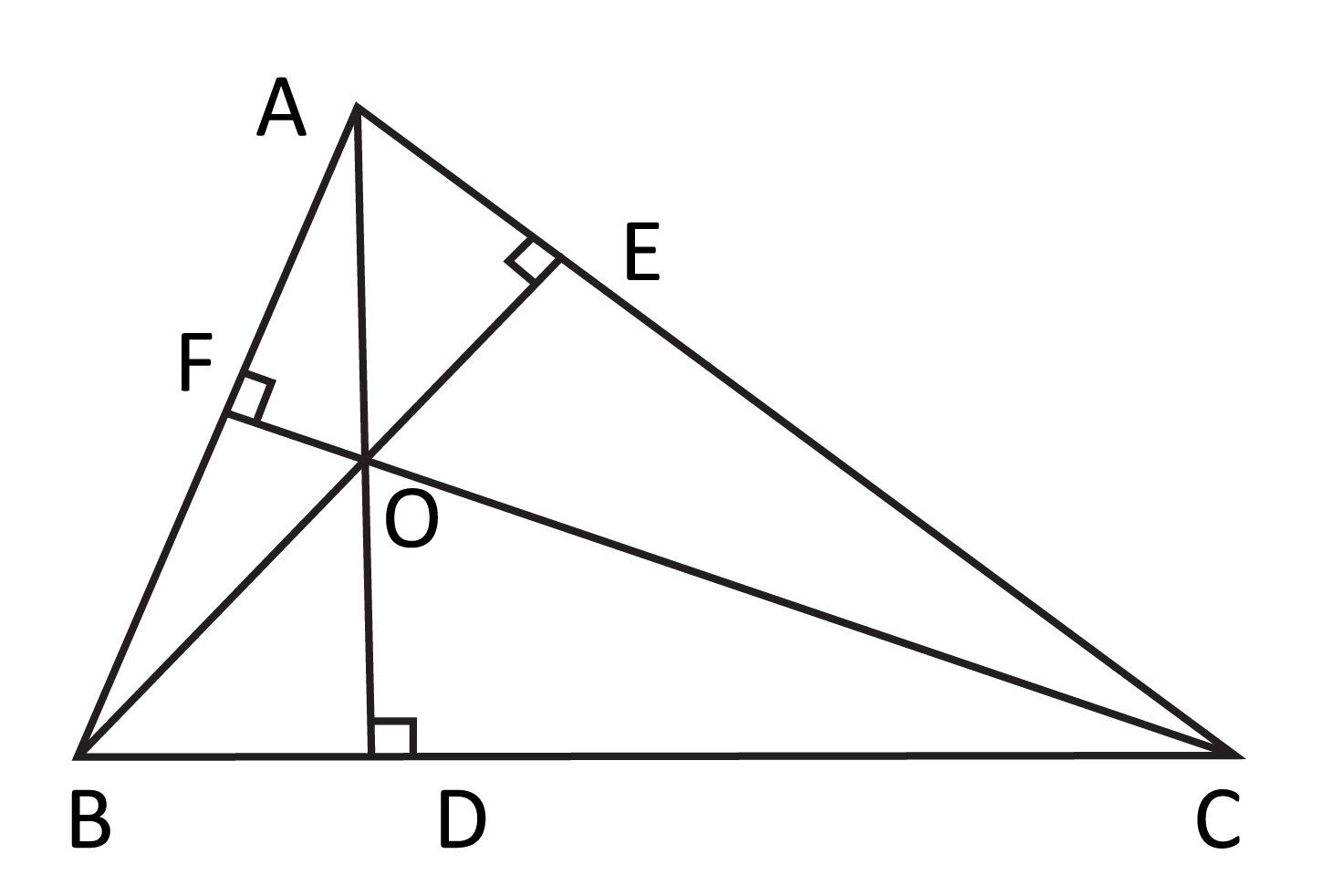
The orthocenter of a triangle is determined by connecting a line from the vertex to the opposite side, so that a 90-degree angle is formed.
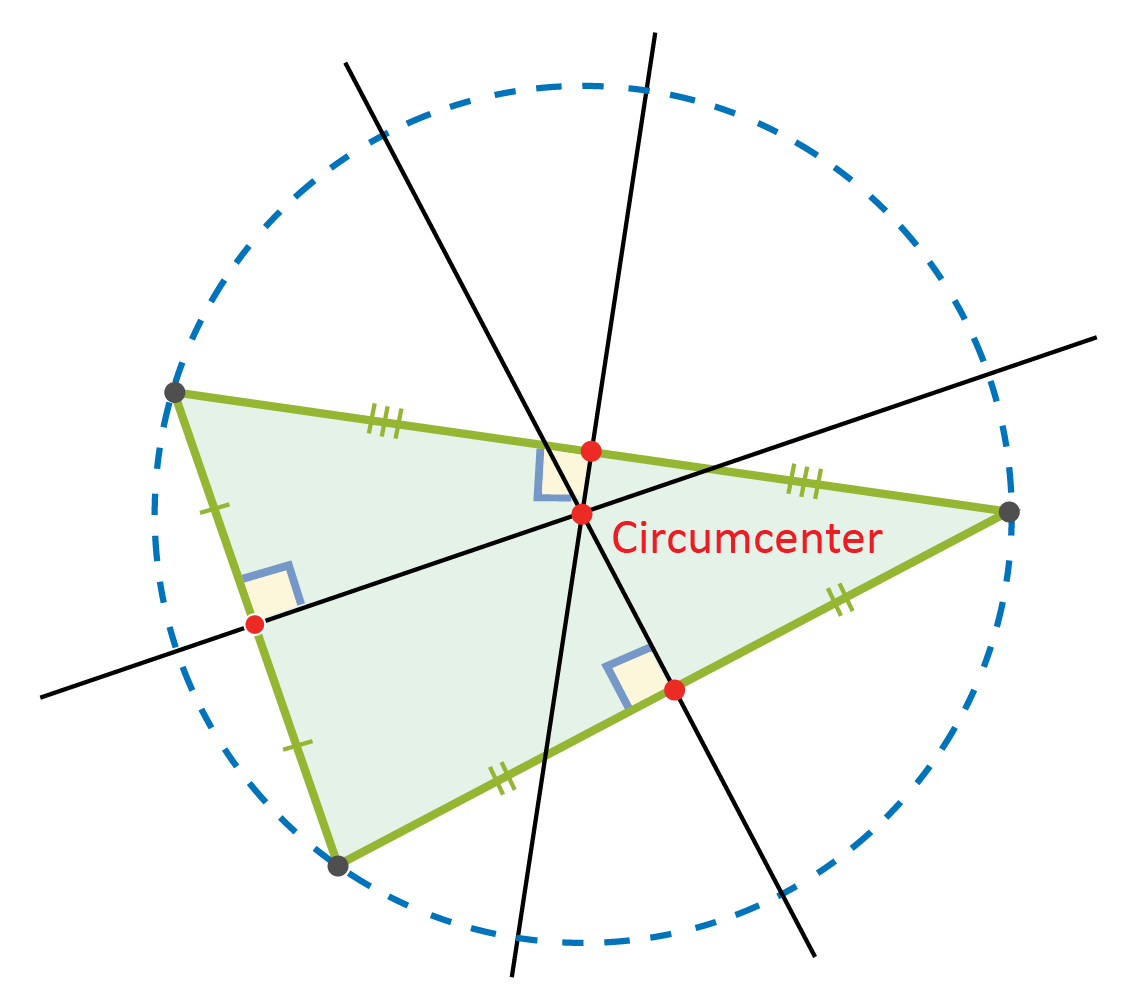
The center of a triangle can be determined by drawing perpendicular bisectors through the midpoint of each side length of a triangle. The center point where all three lines intersect is known as the __________.
The circumcenter of a triangle is located by drawing three perpendicular bisectors from the midpoint of each side length. The intersection point of all three lines is considered the circumcenter.
Determine if the statement is true or false:
The circumcenter is located at the intersection point of three angle bisectors.
The circumcenter is located by creating three perpendicular bisectors. The point where all three lines intersect is the circumcenter.
A city planner is designing a triangular park. She plans to plant an oak tree in the center of the triangle. She decides to calculate the midpoint of each side length by measuring the total distance of each side and then dividing by two. From here, she draws a line from each midpoint to the opposite vertex. The point where all three lines intersect is where she plans to plant the tree.
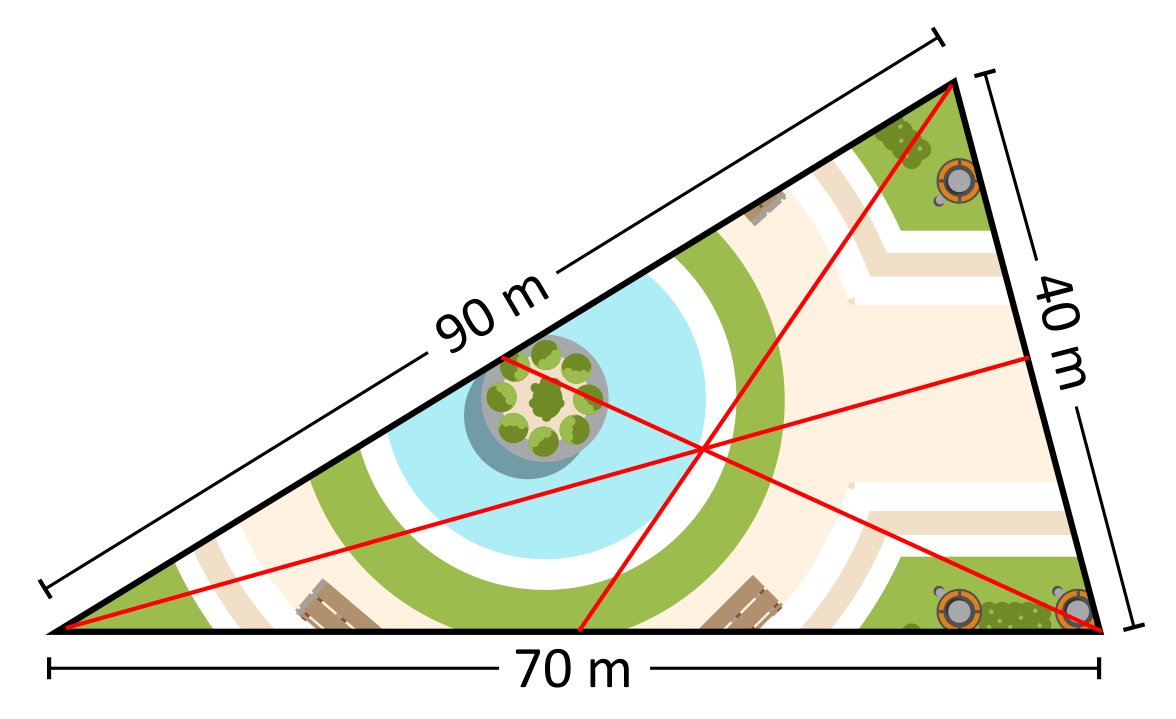
Which method did the city planner use to determine the center of the triangular park?
The centroid is determined by connecting a line from the midpoint of each side length, to the opposite vertex. This is the method that the city planner used to determine where to plant the Oak tree.
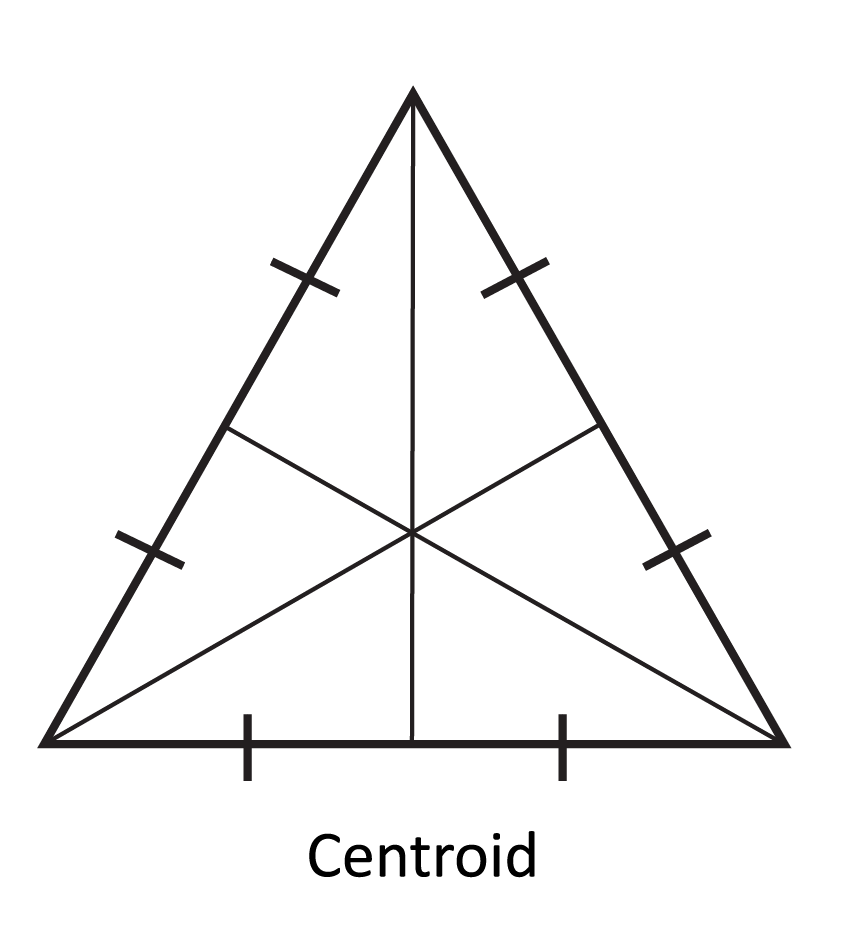
Morgan is building a luxury A-frame cabin in the woods. She wants to determine the “center” of the triangular face of the cabin so that she can fit the pieces of glass in properly. Morgan wants to determine the middle of the triangle by bisecting each interior angle. She plans to create three angle bisectors that extend to the opposite side length of the triangle. Morgan will consider the point where all three lines intersect as the “center” of the triangle.

Which method has Morgan used to determine the center of the triangle?
The incenter of a triangle is found by creating three angle bisectors and then extending these lines to the opposite sides. This is the strategy that Morgan chose in order to find the center of the triangular face of her A-frame cabin.