
Hello! Today we’re going to explore what can happen when a circle and a line or two lines meet.
Let’s start by defining the vocabulary we’ll need.
Secant
A line cutting across a circle that touches two points on the outside of the circle is a secant to the circle.
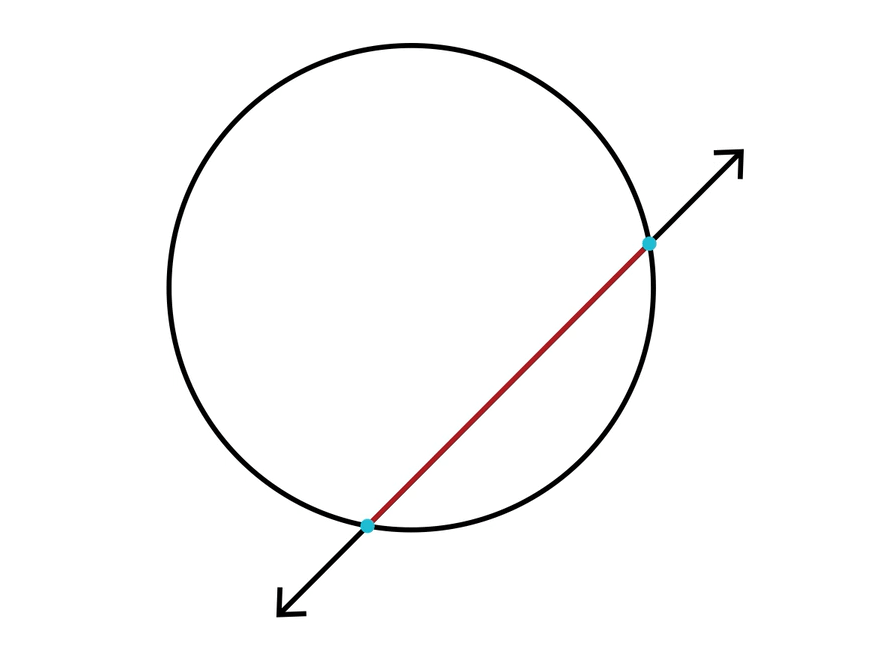
Chord
Here is an example of that. We can see that the line intersects the outside of the circle at two points and creates a line segment between those points, which is highlighted in red. That line segment is called a chord.
Inscribed Angle
We can also have more than one secant to the circle interacting with each other, like this:
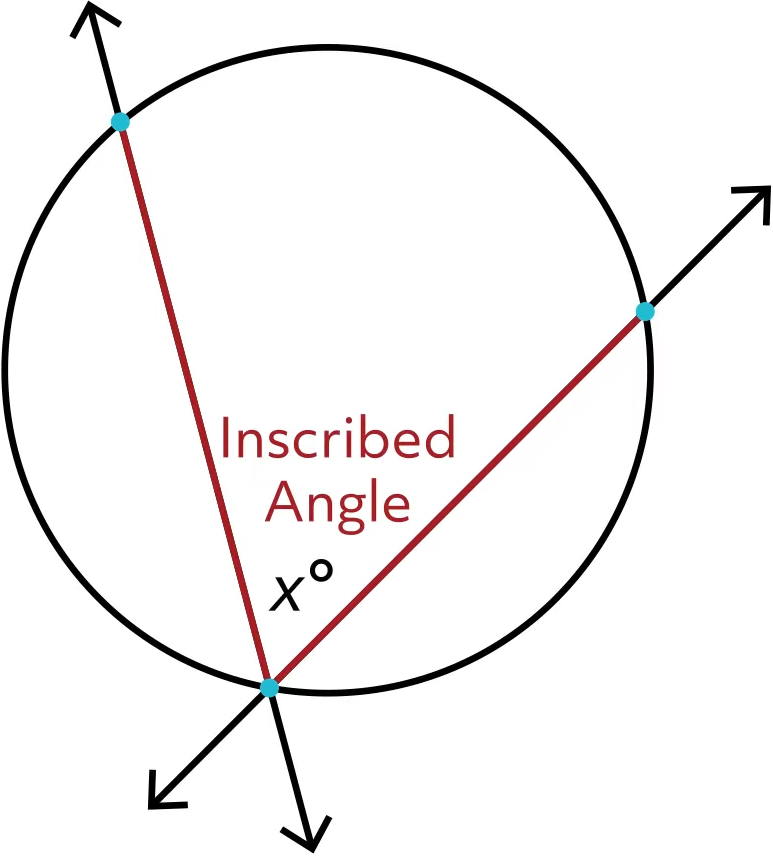
Now our two chords have created an inscribed angle in our circle, which we’ve labeled with an \(x\) and a degree symbol.
Intercepted Arc
Across from the angle is the part of the circle between the points where the chords intersect the circle, highlighted in yellow. This is the intercepted arc. We can find the measure of our inscribed angle \(x\) if we know the length of the intercepted arc in degrees.
Central Angle
The intercepted arc is the same measure as the central angle that uses the same two points as our inscribed angle, but with its vertex at the center of the circle.
The central angle measures 120°, so our intercepted arc also measures 120°. Notice how the central angle is quite a bit “wider” than our inscribed angle. That’s because it is! In fact, it’s exactly twice as wide. That means we can find our inscribed angle by dividing our central angle by two, which means our inscribed angle is \(120^{\circ}\div 2\), or 60°!
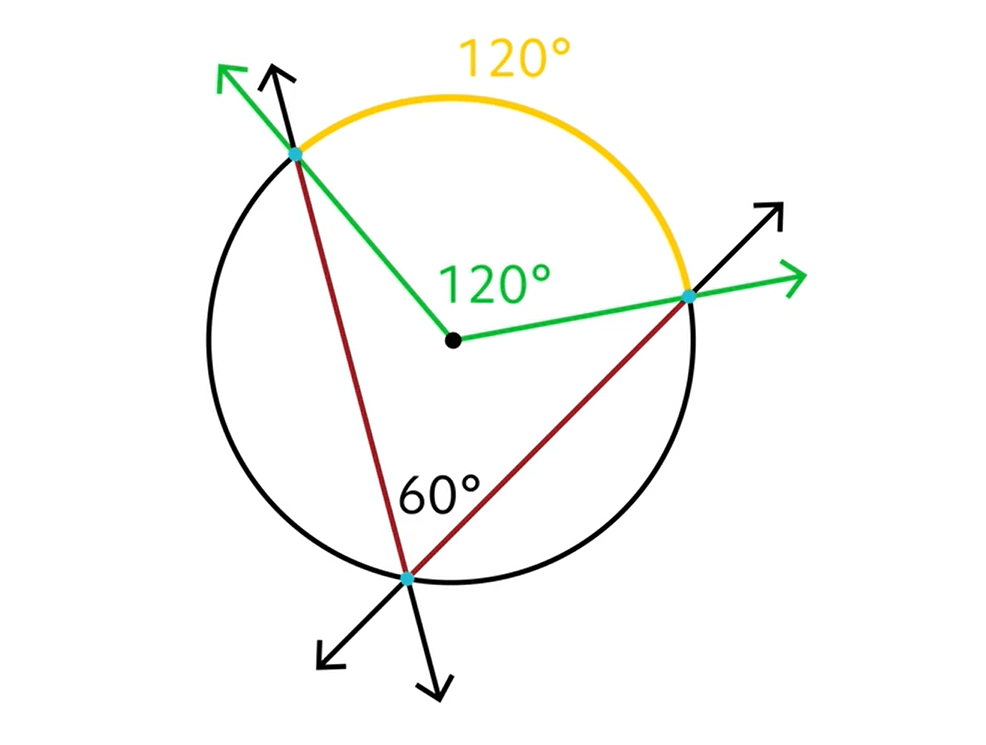
The central angle is always twice as big as the inscribed angle when our inscribed angle has its vertex on the circle itself. This also means we can find the central angle or the intercepted arc easily if we know the measure of the inscribed angle—all we need to do is double the measure of the inscribed angle!
But what if our two secant lines meet at a vertex that is inside or outside the circle instead of directly on it?
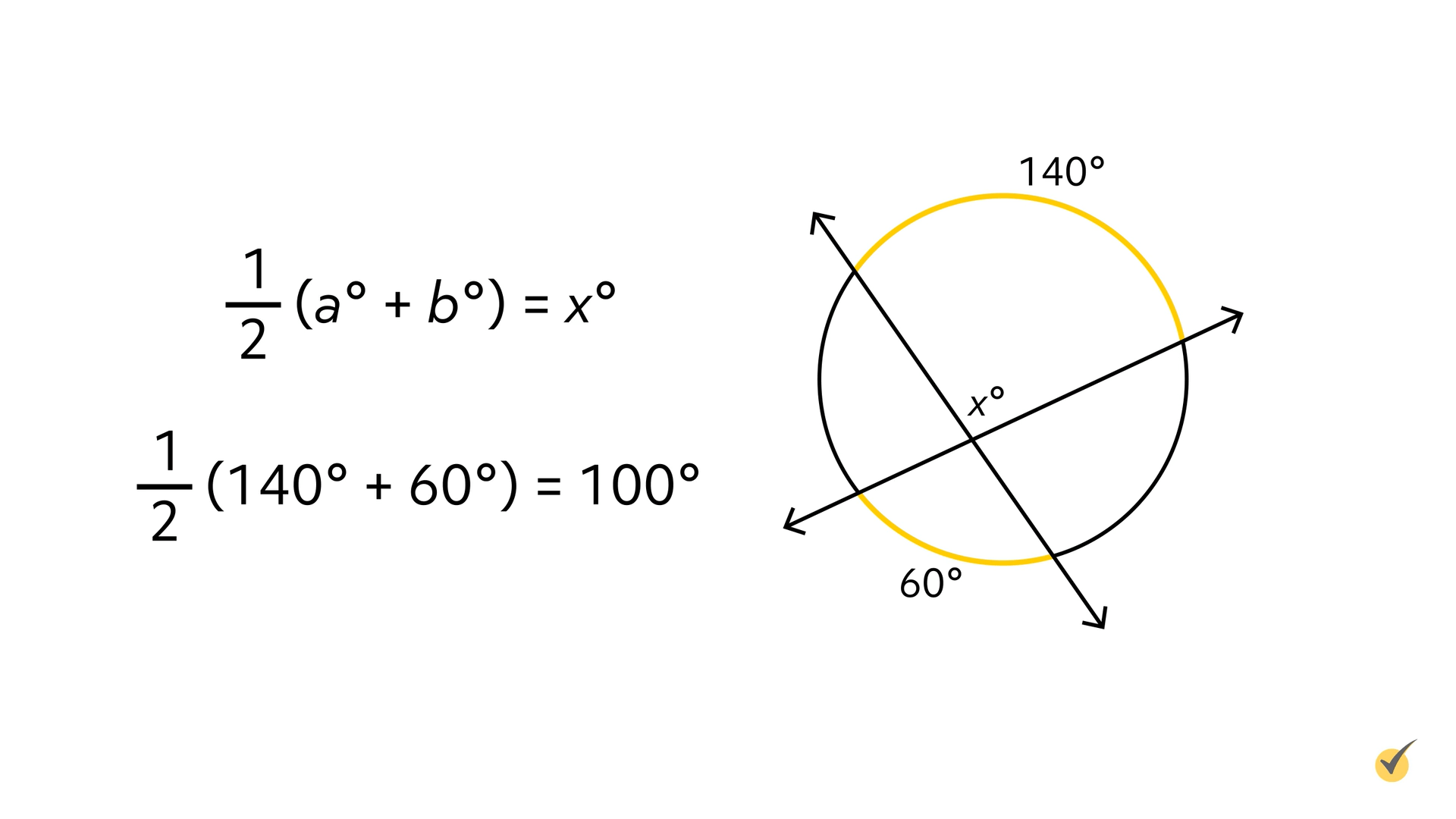
Each one of these has a formula for finding the measure of \(x\) if we know the measure of our intercepted arcs in degrees. Let’s start when our inscribed angle is inside the circle. In this case the measure of the inscribed angle is half of the sum of the measures of the intercepted arcs (in this case, \(a^{\circ}\) and \(b^{\circ}\)).
So if we know that \(a^{\circ}\) measures 140° and \(b^{\circ}\) measures 60°, we simply add them together and take half of that:
\(\frac{1}{2}(140^{\circ}+60^{\circ})=100^{\circ}\)
If our inscribed angle ends up outside the circle, it works similarly, but we need to use subtraction instead of addition before multiplying by \(\frac{1}{2}\).
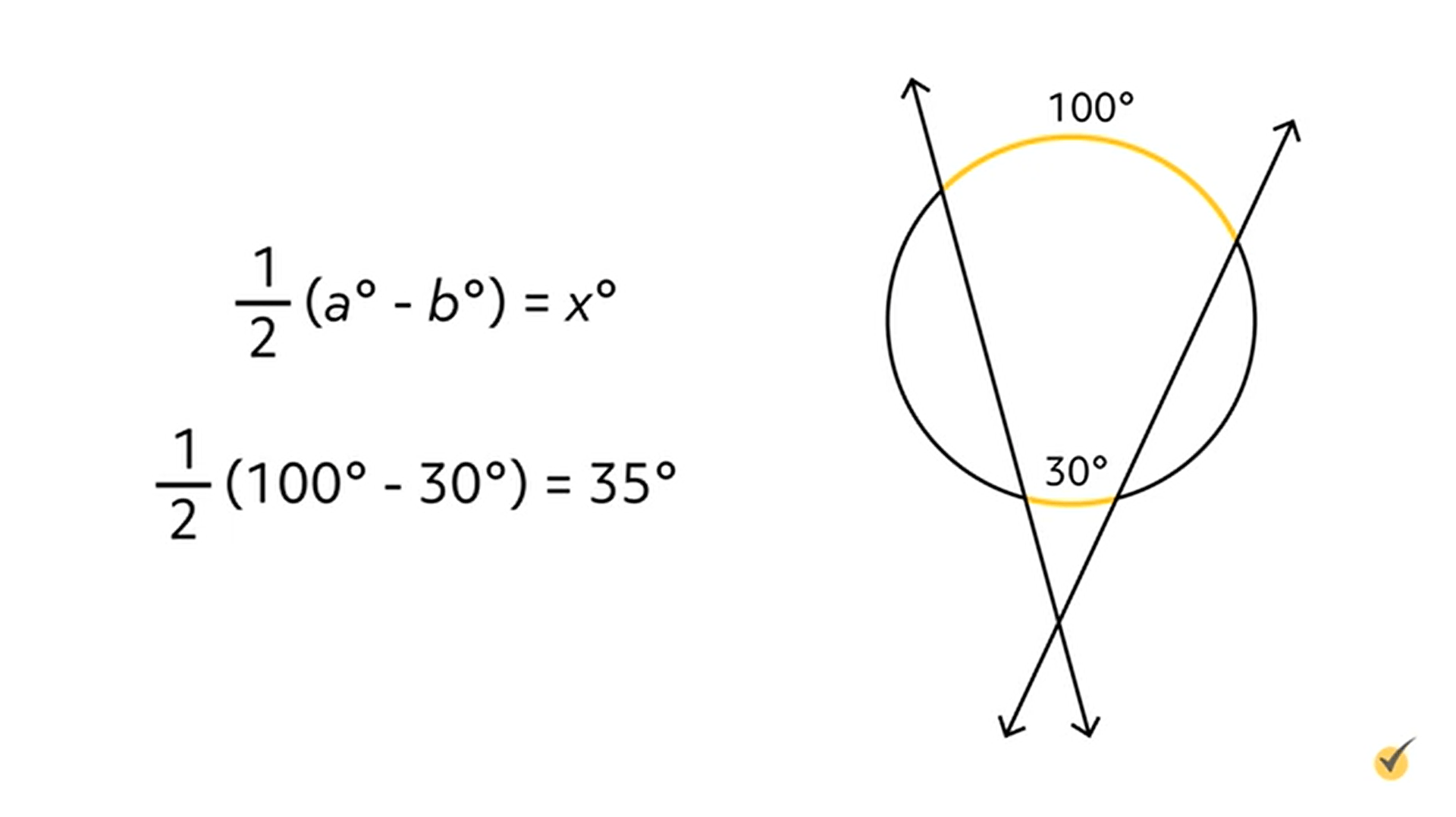
Our secants create two intercepted arcs between them. Here they’re again shown as \(a^{\circ}\) and \(b^{\circ}\).
If we know the measure of the intercepted arcs in degrees, we can plug them in to find the measure of \(x^{\circ}\):
\(\frac{1}{2}(100^{\circ}-30^{\circ})=35^{\circ}\)
We can do a little common sense check to make sure we’re using the right version of this formula. If we accidentally used the addition formula, we would end up with an angle measuring 65°, which appears to be way too big for our little angle. Be careful, though. Problems on the standardized tests are sometimes not drawn to scale – watch for a warning to that effect on any problem you do.
Tangent Lines
When a line and circle interact, sometimes secants aren’t created. If a line passes by a circle and only touches it in one point, it creates what we call a line that is a tangent to the circle. The point where the line and the circle touch is called the point of tangency.
We see the word tangential outside of math sometimes too, describing a topic that is only slightly related to the topic being discussed. Here it means the line that is touching the circle in the slightest way possible – only at one point.
Anyway, looking closely at our diagram, we can see a radius of the circle meeting our tangential line at a 90° angle. For our line to be truly tangent, this must be true. If our line isn’t exactly perpendicular to the radius at the point of tangency it will actually touch the circle twice, though possibly very close together. This would actually create a secant instead of a tangent line. We can see that by zooming in on a circle that shows the angles that are just a few degrees away from 90°:
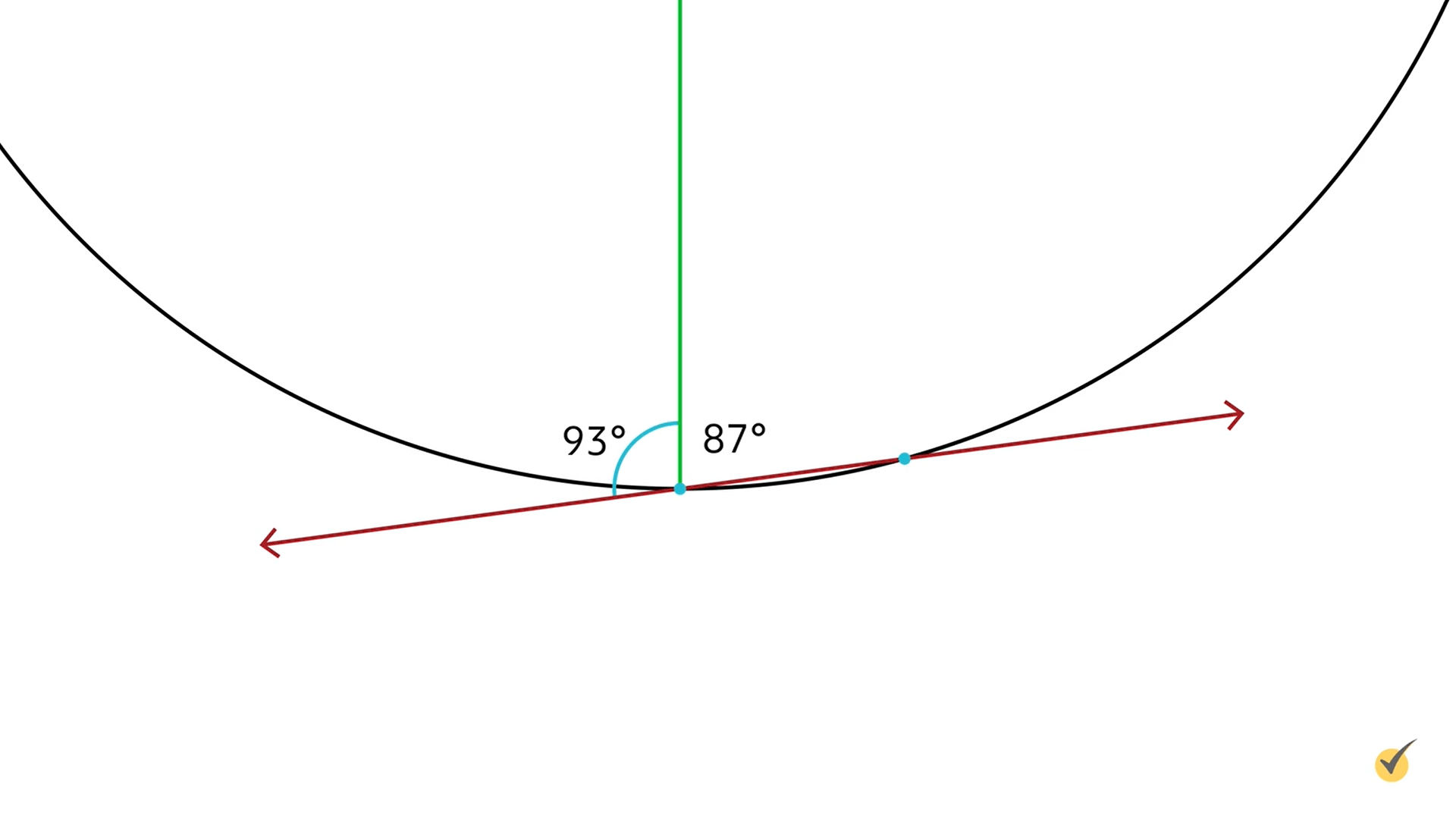
Even if the angle were even closer to 90°, such as 90.1° and 89.9° this would still happen, though it would be really hard to show on a diagram!
I hope this video on secants, chords, and tangents was helpful! Thanks for watching, and happy studying!
Secants, Chords, and Tangent Practice Questions
Match the correct name to each line.
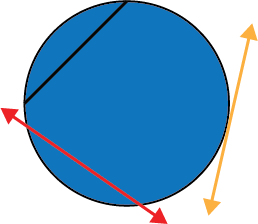
Secant: A line that touches two points on the circumference of the circle.
Chord: A line segment that joins two points on the circumference of the circle.
Tangent: A line that touches the circle’s circumference only once.
What is the value of \(x\)?
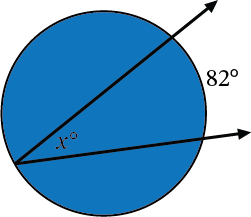
In the figure, \(x\) is the measure of an inscribed angle. An inscribed angle is half of the intercepted arc. In this case, the intercepted arc is \(82°\). Half of \(82°\) is \(41°\). So, the inscribed angle is \(41°\).
What is the measure of the interior angle with a measure of \(x°\)?
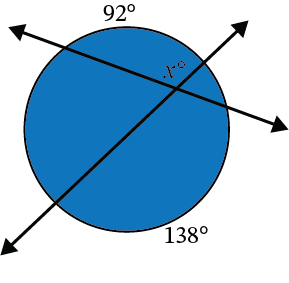
The interior angle, \(x\), can be determined using the formula \(x=\frac{1}{2}(a°+b°)\), where \(a\) and \(b\) are the intercepted arcs.
\(x=\frac{1}{2}(92°+138°)\)
\(x=\frac{1}{2}(230°)\)
\(x=115°\)
A flashlight is shining out into the forest at \(x°\). The corresponding intercepted arcs formed by the shining light are \(21°\) and \(162°\). What is the angle of light being projected from the flashlight?
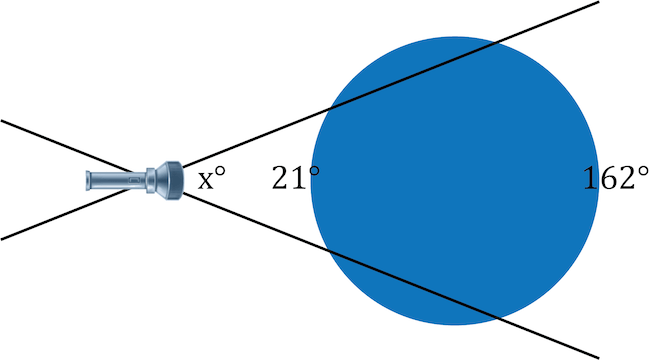
The angle of \(x\) can be determined using the formula \(x=\frac{1}{2}(a°-b°)\) where \(a\) and \(b\) represent the intercepted arcs.
\(x=\frac{1}{2}(162°-21°)\)
\(x=\frac{1}{2}(141°)\)
\(x=70.5°\)
The angle of light shining from the flashlight is \(70.5°\).
You are welding circular earrings to sell at your local farmers market. Each earring is circular with two bars through the circle. You want each earring to look the same, so you want to calculate the exact angle measure of the interior angle. The measure of the two arcs intercepted by the bars are \(72°\) and \(70°\), respectively. What is the measure of angle \(x\)?
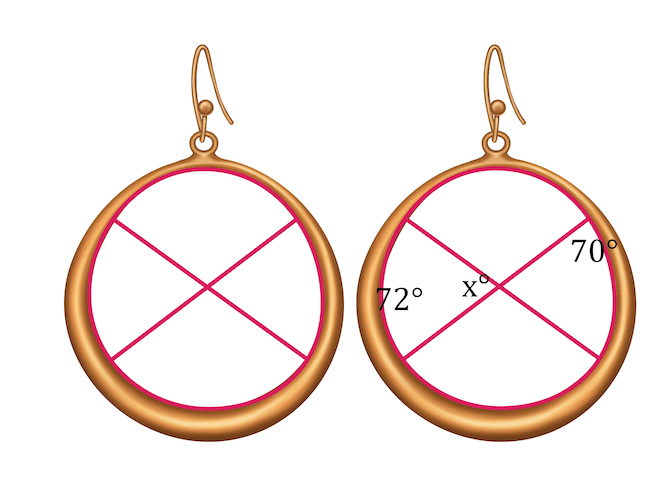
The unknown angle is inside of the circle, so the angle \(x\) can be calculated using the formula \(x=\frac{1}{2}(a°+b°)\), where \(a\) and \(b\) represent the intercepted arcs.
\(x=\frac{1}{2}(72°+70°)\)
\(x=\frac{1}{2}(142°)\)
\(x=71°\)