General Rules for Triangles
Hi, and welcome to this video on the General Rules of Triangles.
Today, we’re going to look at the four most important properties of triangles.
The first property is known as the triangle inequality theorem. It states that no side of a triangle can be longer than the other two sides added together. Let’s look at this triangle.
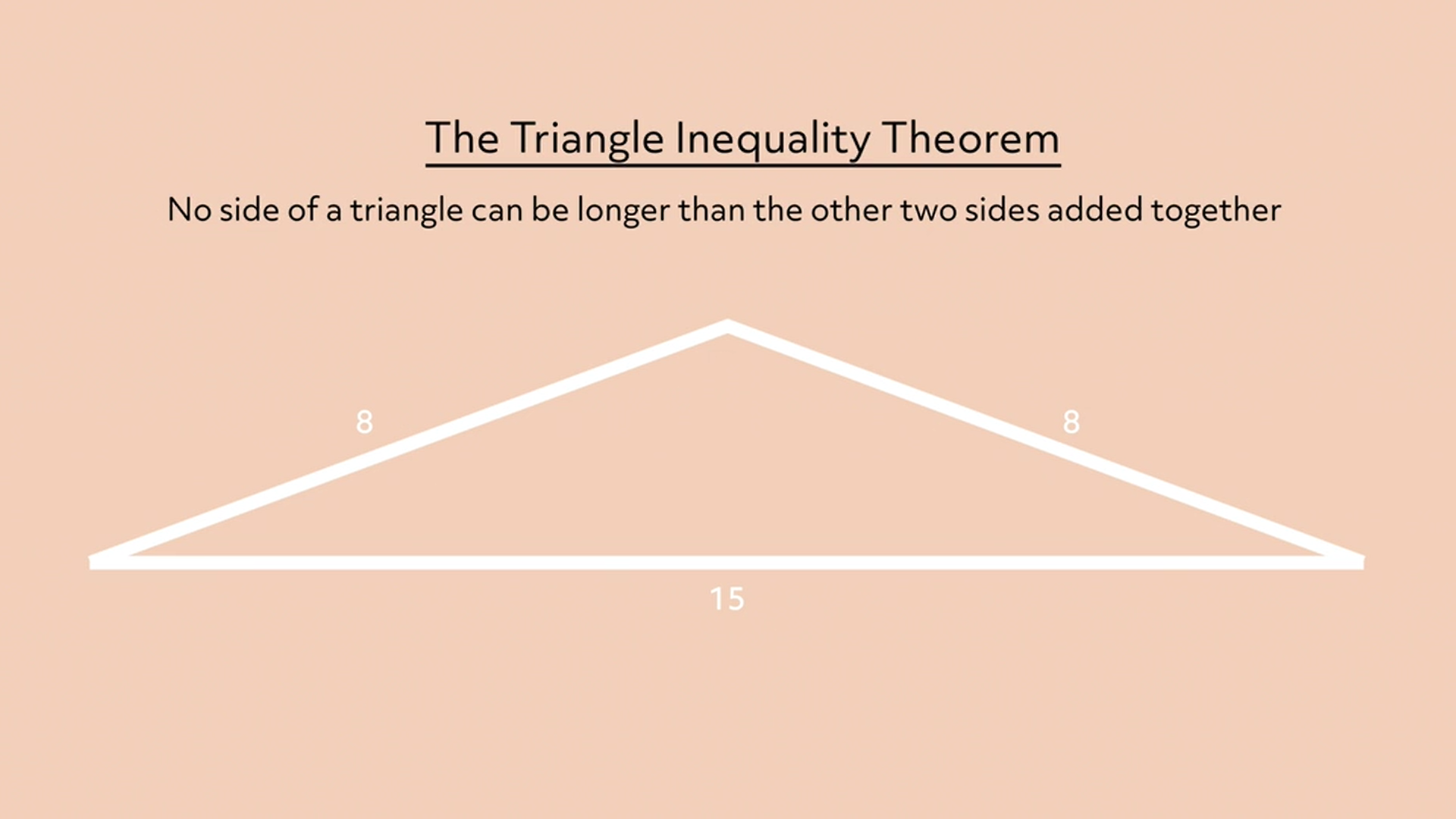
As you can see, one of the sides is a lot longer than each of the other two sides. But when we measure the sides, the length of the smaller sides added together is still longer than the length of the longer side.
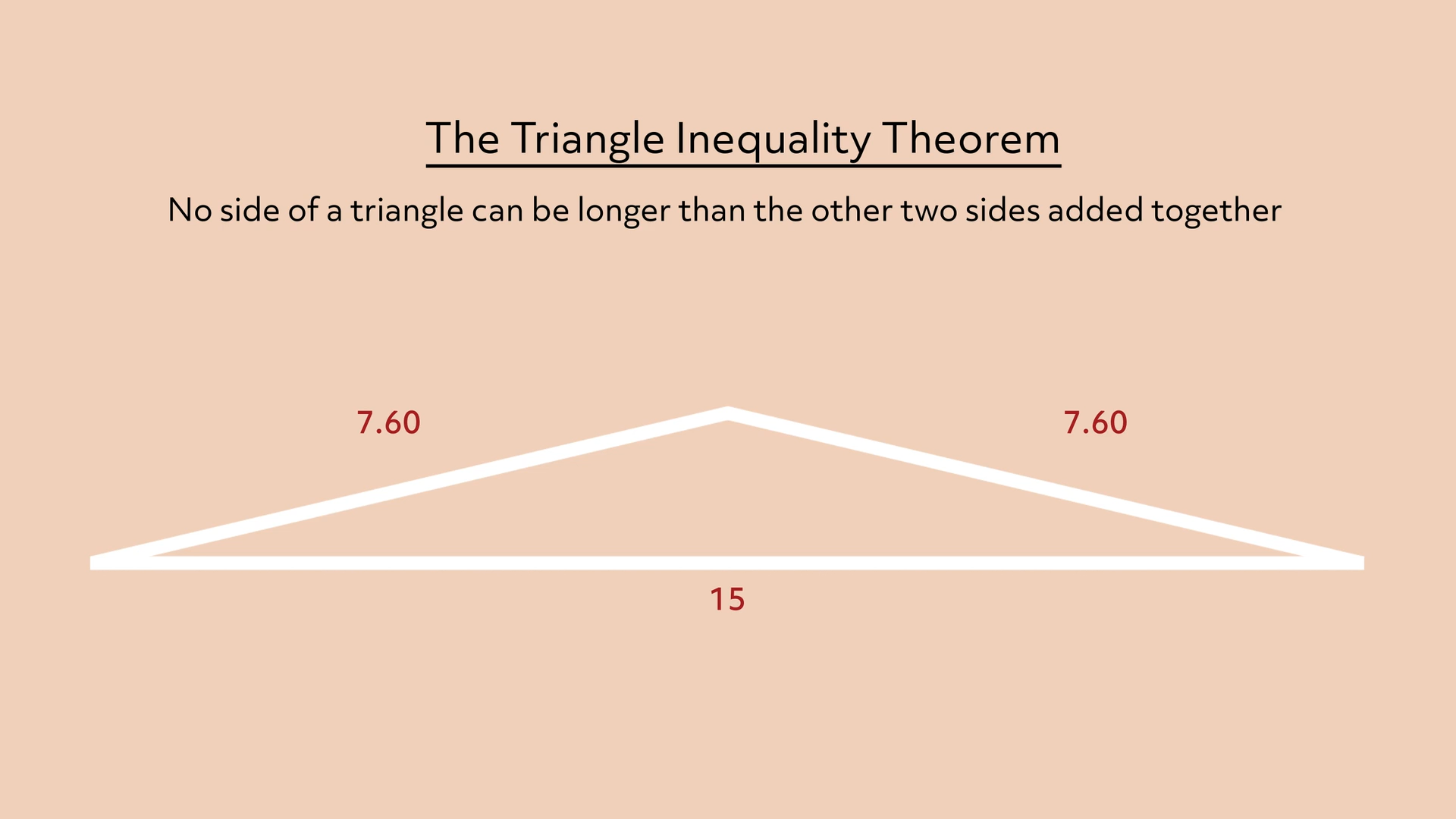
If I pushed the top of this triangle lower, the sides would get a bit shorter but they’d still add up to a little more than 15.
If I flattened them completely so that they’d form a straight line segment they would add up to 15, but then we wouldn’t have a triangle anymore.
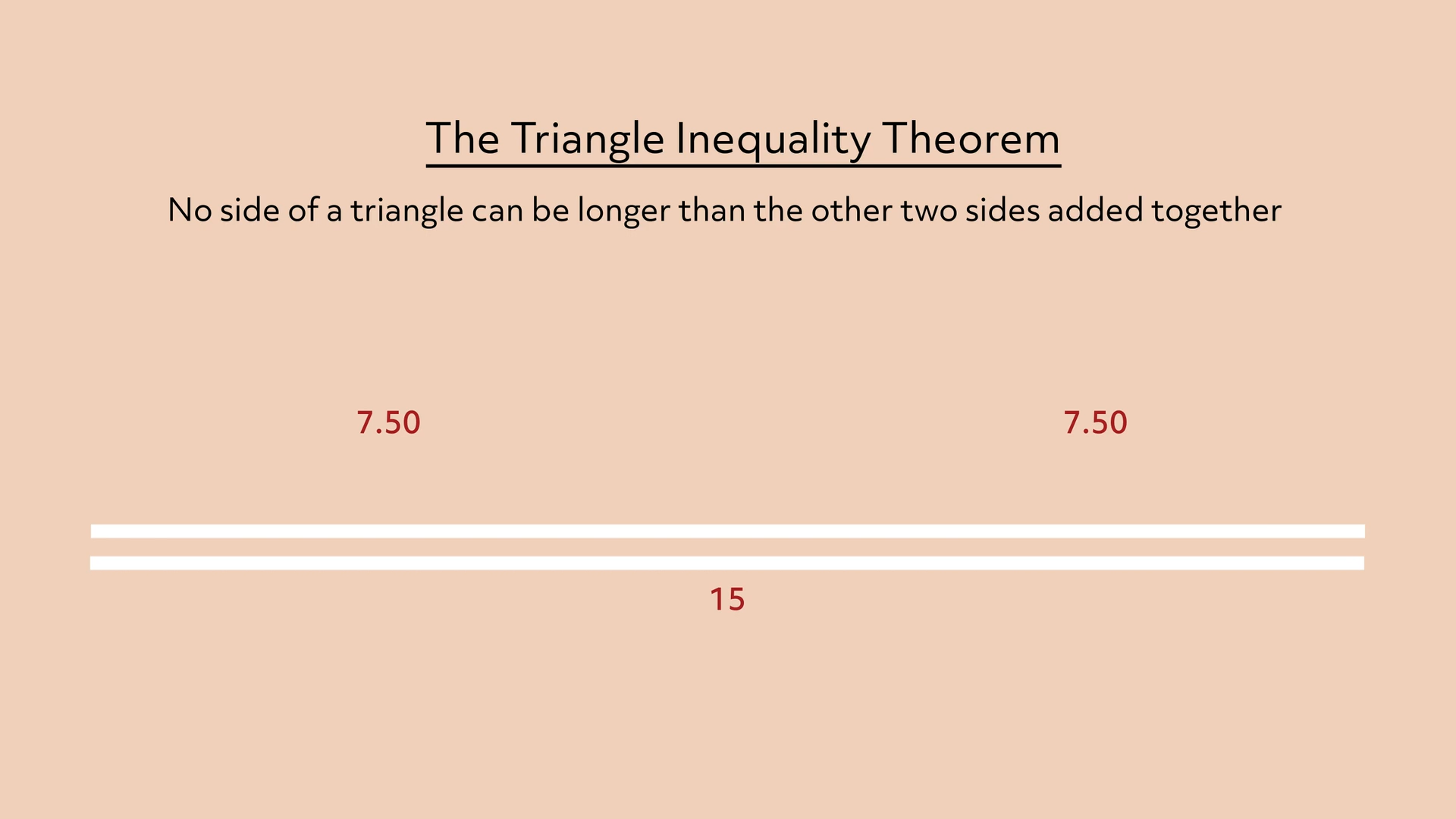
Feel free to try it yourself. Cut a few straight sticks of different lengths and try to arrange them into a triangle with one of the sides longer than the other two combined. There’s just no way to make it connect as a triangle!
For our second property, let’s move from a rule about the sides of a triangle to one about the angles inside the triangle. You probably remember that the angles inside any triangle always add up to 180°. Since that’s true, we can’t have a triangle with two angles that are 90° (a right angle) or more than 90° (an obtuse angle). The reason why is simple – there wouldn’t be any degrees left to make the third angle:
\(90^{\circ}+90^{\circ}+\text{ third angle}=180^{\circ}\)The third angle here would have to be 0°, and an angle with that measure isn’t any angle at all. And it’s even worse if we use obtuse angles:
\(100^{\circ}+95^{\circ}+\text{ third angle}=180^{\circ}\)Here, our third angle would need to be –15°! That’s just not going to work to make a triangle!
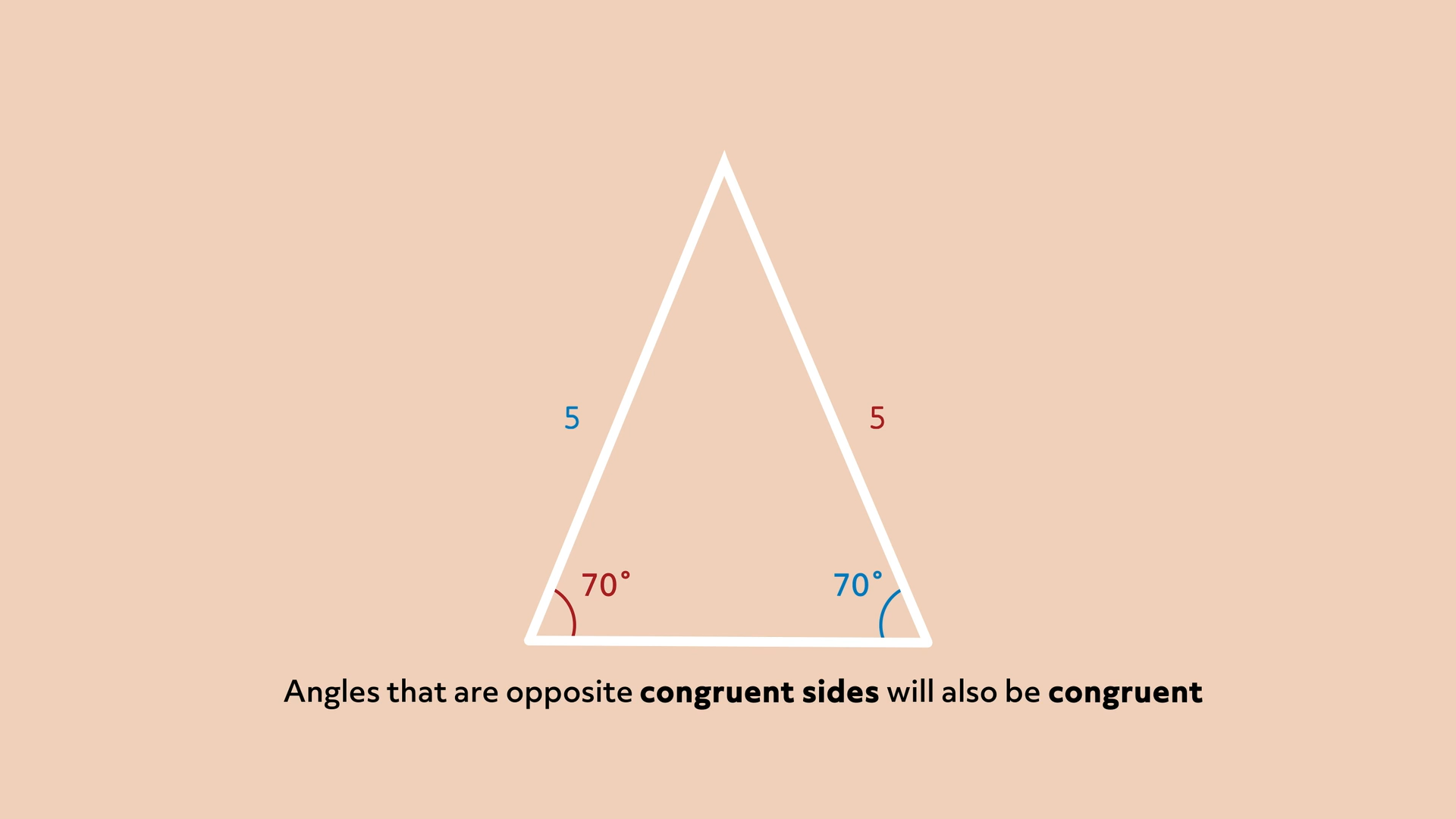
For the third property, we’re going to examine the relationship between the sides of a triangle and their lengths. But first, we need to define the term congruent. Congruent sides of a triangle are sides that are the same length. The length of a side congruent to a side that measures 5 centimeters would be 5 centimeters. The same is true for angles.
In any triangle, if we have two sides that are congruent, then the two angles that are opposite those sides will also be congruent. This is always true no matter how long the two sides are or how tiny or big the angles are. We can see that in this triangle, which is an isosceles triangle.
For our final property, let’s look at this triangle:
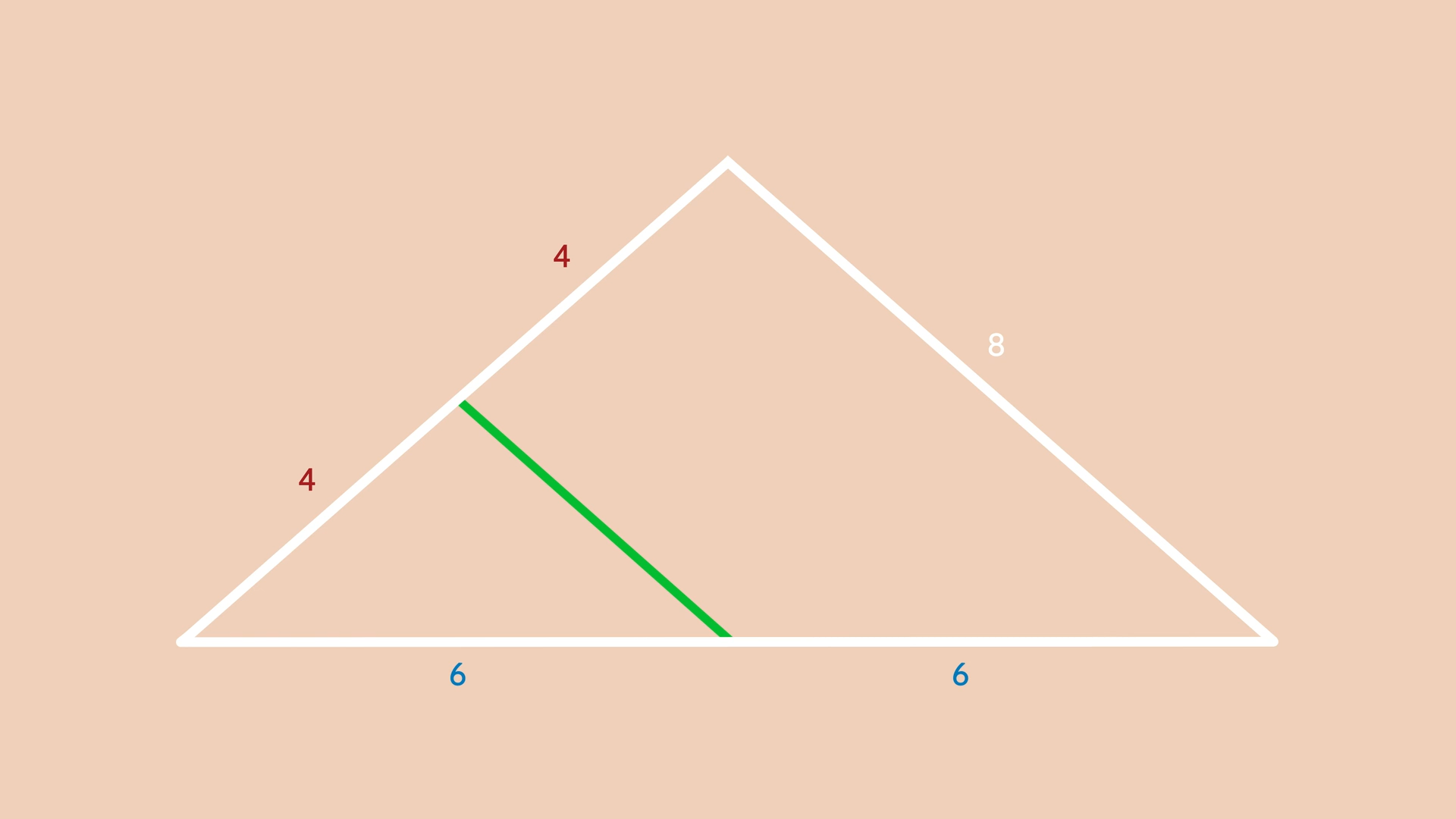
Here, we have a line segment in green that connects the midpoint of one side to the midpoint of another side. Whenever you do this in a triangle, the line segment you created is always half the length of the side you didn’t bisect. Not only that, it’s parallel to that side too!
As you can see, triangles are amazing shapes with all sorts of cool properties.
Thanks for watching, and happy studying!
Triangle Practice Questions
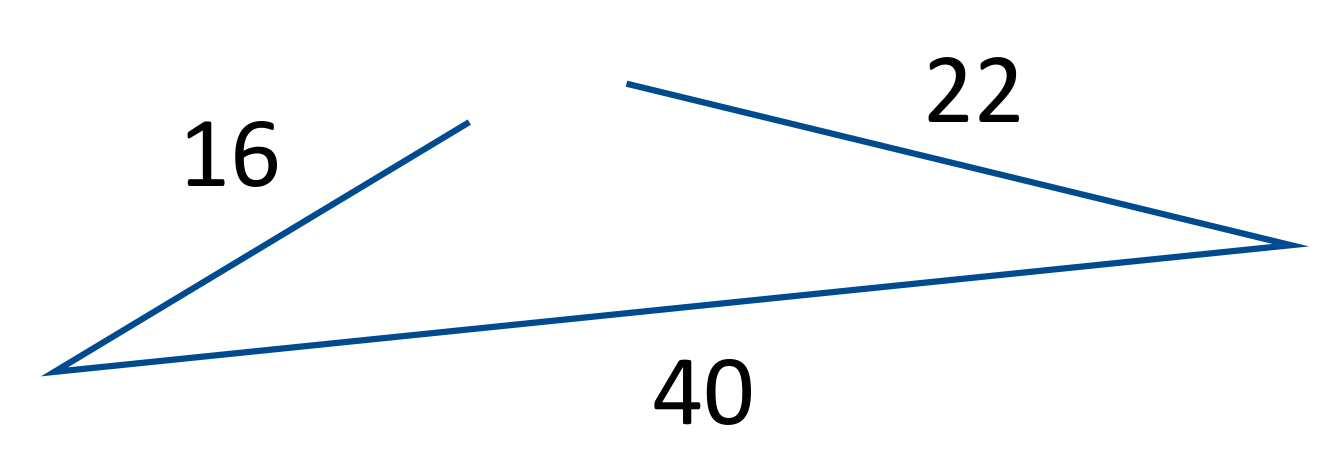
The theorem stating that no side of a triangle can be longer than the other two sides added together is known as the:
Pythagorean Theorem
Equilateral Triangle Theorem
Triangle Inequality Theorem
Congruent Triangle Theorem
A triangle cannot have one side that is longer than the sum of the other two sides. For example, a shape with side lengths 16, 22, and 40 would not connect as a triangle. The two shorter side lengths are not long enough to reach and connect to form a triangle.
The interior angles of a triangle will always have a sum of _________.
180°
150°
90°
360°
The interior angles of a triangle will always add to 180°. This means that a triangle cannot have more than one 90° angle, and no more than one obtuse angle.
The following isosceles triangle shows two congruent side lengths, therefore angle _____ and angle _____ will be congruent.
Angle C and Angle A
Angle C and Angle B
Angle A and Angle B
No angles will be congruent
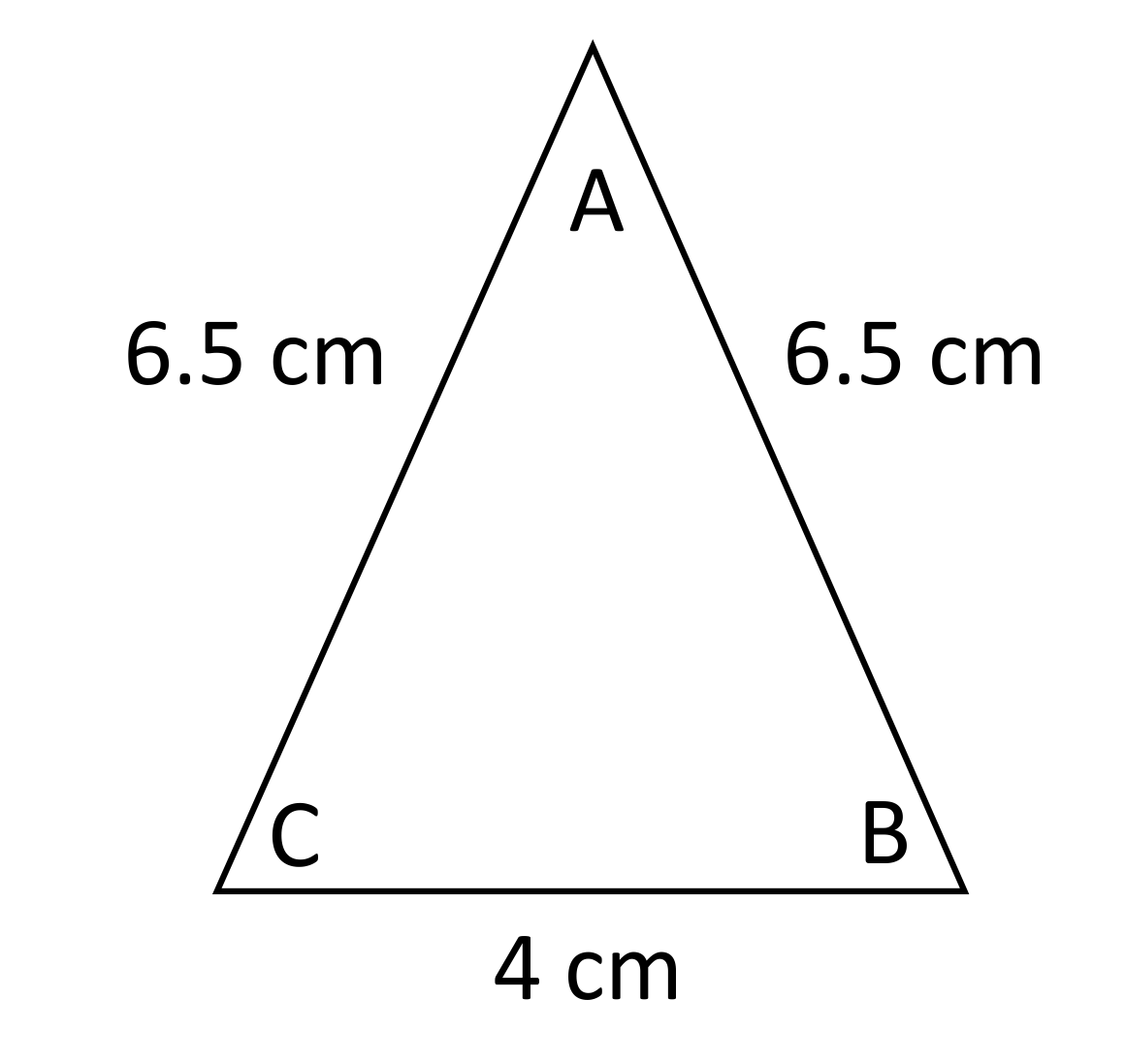
If two sides lengths of a triangle are congruent, then the corresponding angles will also be congruent.
Beth is creating a stone walking path through a triangular green space in her city. She sketches a diagram of the park and labels it triangle ABC. Beth wants the path to start at the midpoint of side AB and end at the midpoint of side BC as drawn below. If this is how the path is designed, what will be true regarding the length of DE compared to AC?
DE will be twice as long as AC.
DE will be congruent to AC.
DE will be exactly one-fourth the length of AC.
DE will be exactly half the length of AC.
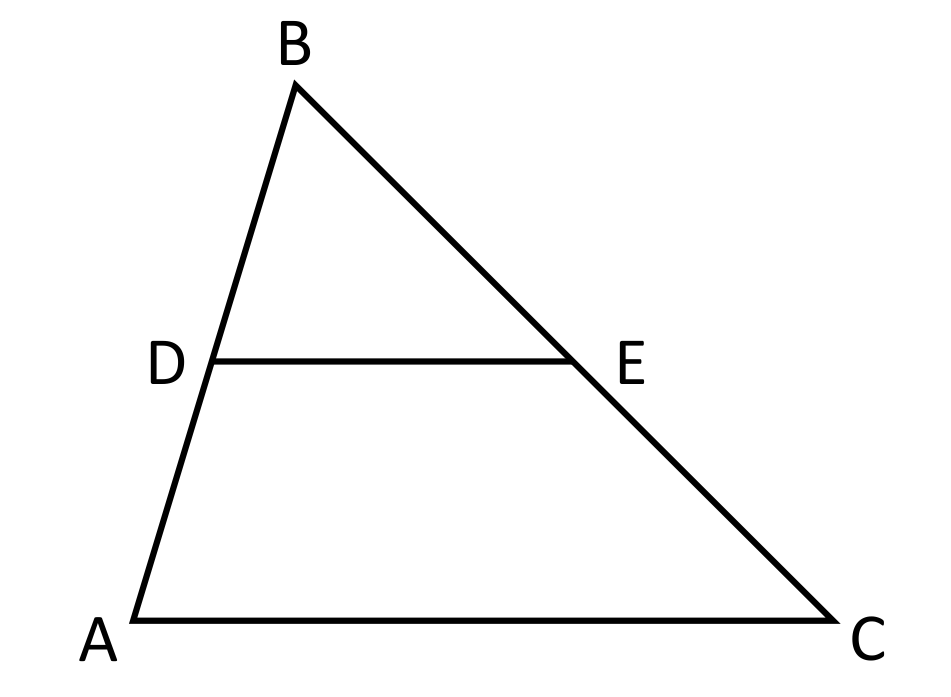
If you connect the midpoint of one side of the triangle to the midpoint of another side, the distance from point to point will be exactly half of the side that you did not bisect. In this example, the distance of DE will be exactly half of AC.
Point A is the midpoint of XY, and point B is the midpoint of YZ. If the distance of AB is half the distance of XZ, determine the value of x.
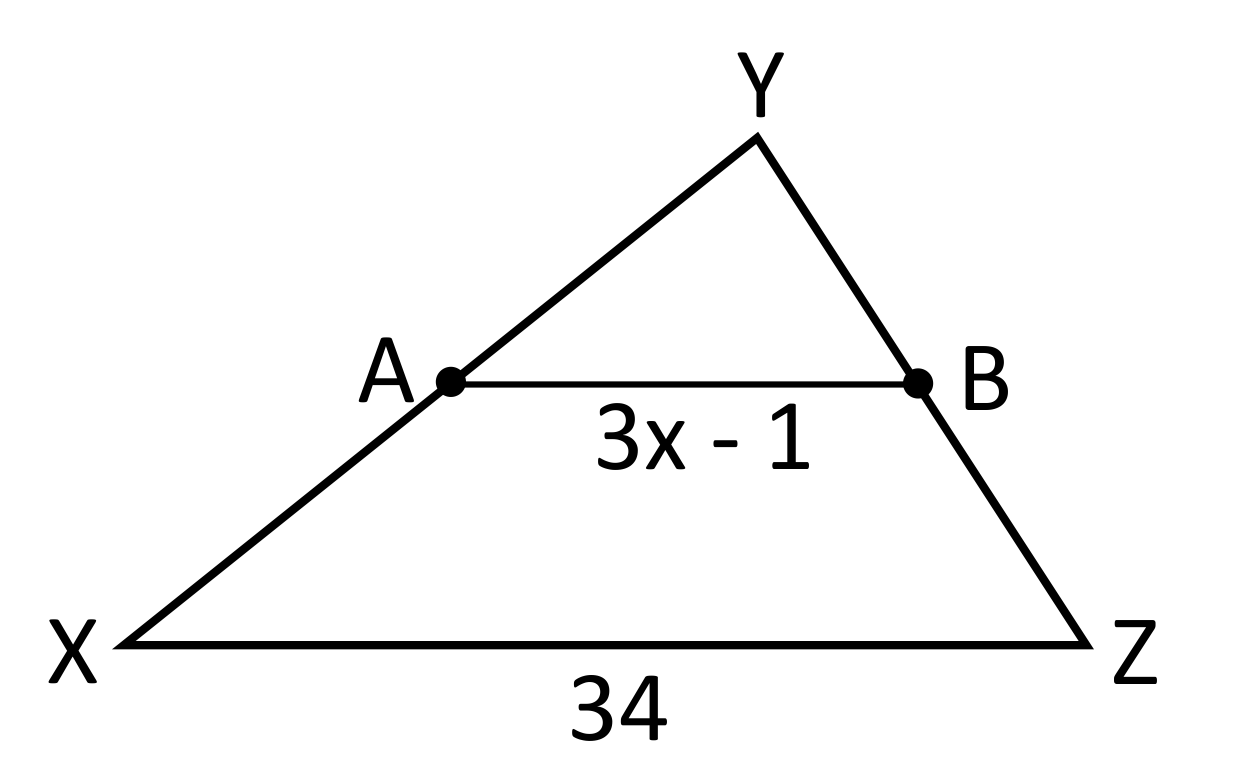
When you connect the midpoint of one side of a triangle to the midpoint of another side of the triangle, the line segment will be exactly half of the side length that was not bisected. In this example, AB is exactly half the distance of XZ. This means that \(3x-1\) is half of \(34\). Half of \(34\) is \(17\), so we can set \(3x-1\) equal to \(17\) and solve for \(x\). \(3x-1=17\) becomes \(3x=18\), and when both sides of the equation are divided by \(3\), the result is \(x=6\).