
A parabola is the distinct shape of a quadratic equation when it is graphed.
In this video, we’ll give you some clues found in quadratic equations that can tell you more about the parabolas they graph.
Symmetry
So, the symmetry of a parabola is due to the squared term in the quadratic equation. However, there is one point on the parabola that does not have a “mirror image.” This point is called the vertex, and is notated by the ordered pair \((h,k)\). The vertex is either the maximum or minimum value of the parabola, depending on which direction the parabola opens.
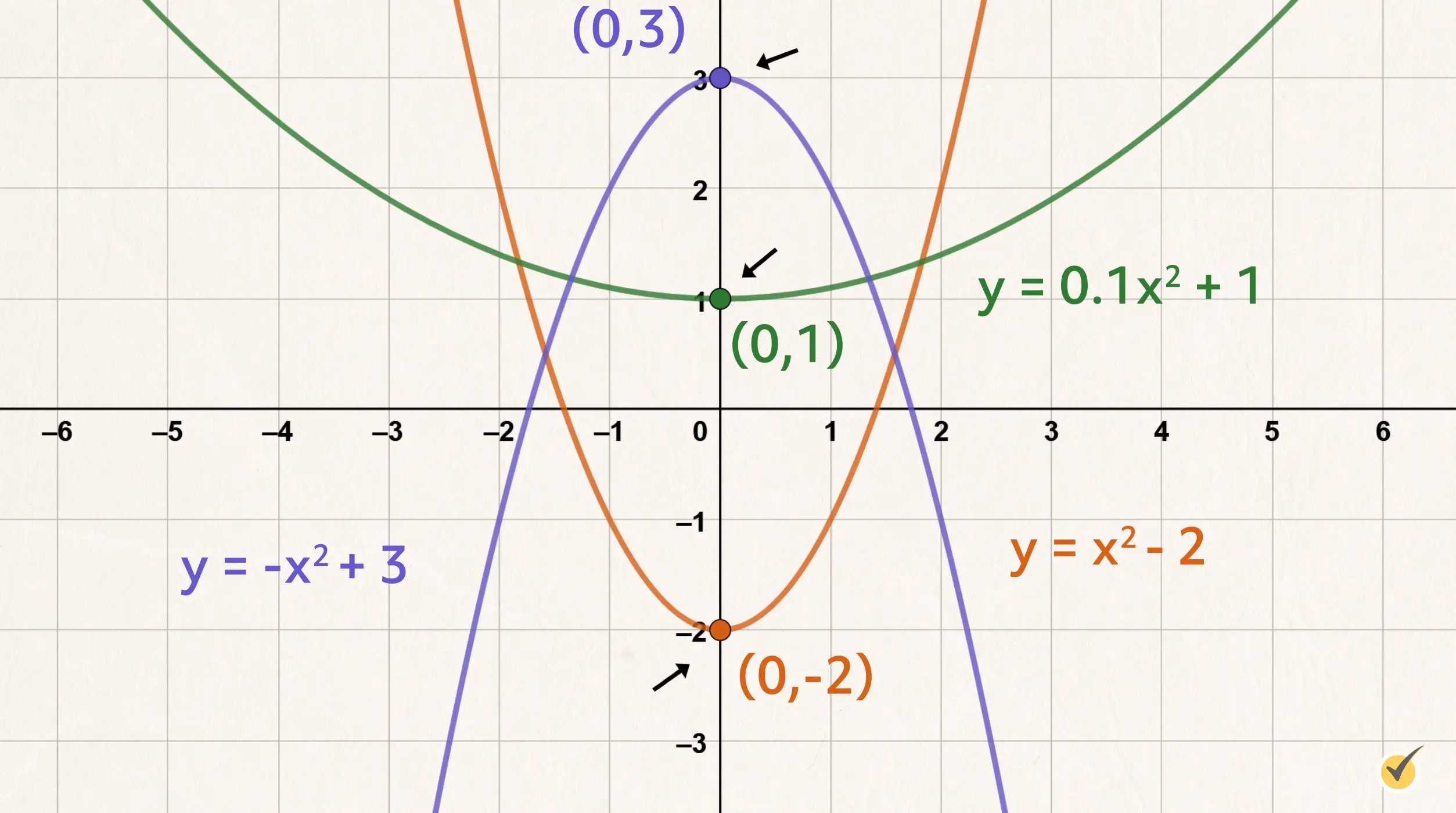
When the \(x\)-variable is squared in a quadratic equation, the parabola will “open” either up or down. Picture the two symmetric branches of the graph extending away from the vertex in the same direction; either up, towards positive infinity on the \(y\)-axis, or down, towards negative infinity on the \(y\)-axis.
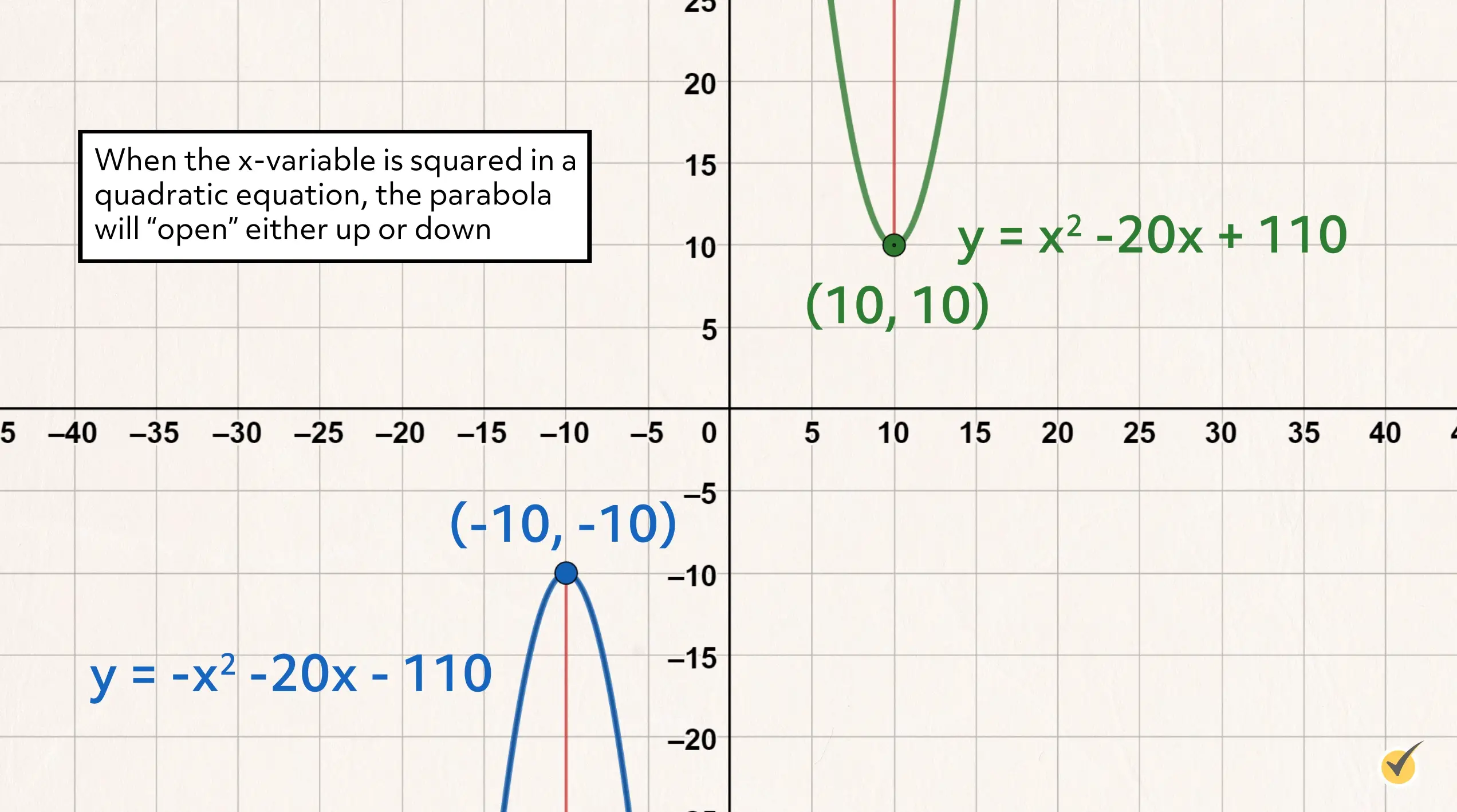
However, when the \(y\)-variable is squared in a quadratic equation, the parabola will “open” either to the right, as both branches extend away from the vertex towards positive infinity on the \(x\)-axis, or to the left, toward negative infinity on the \(x\)-axis.
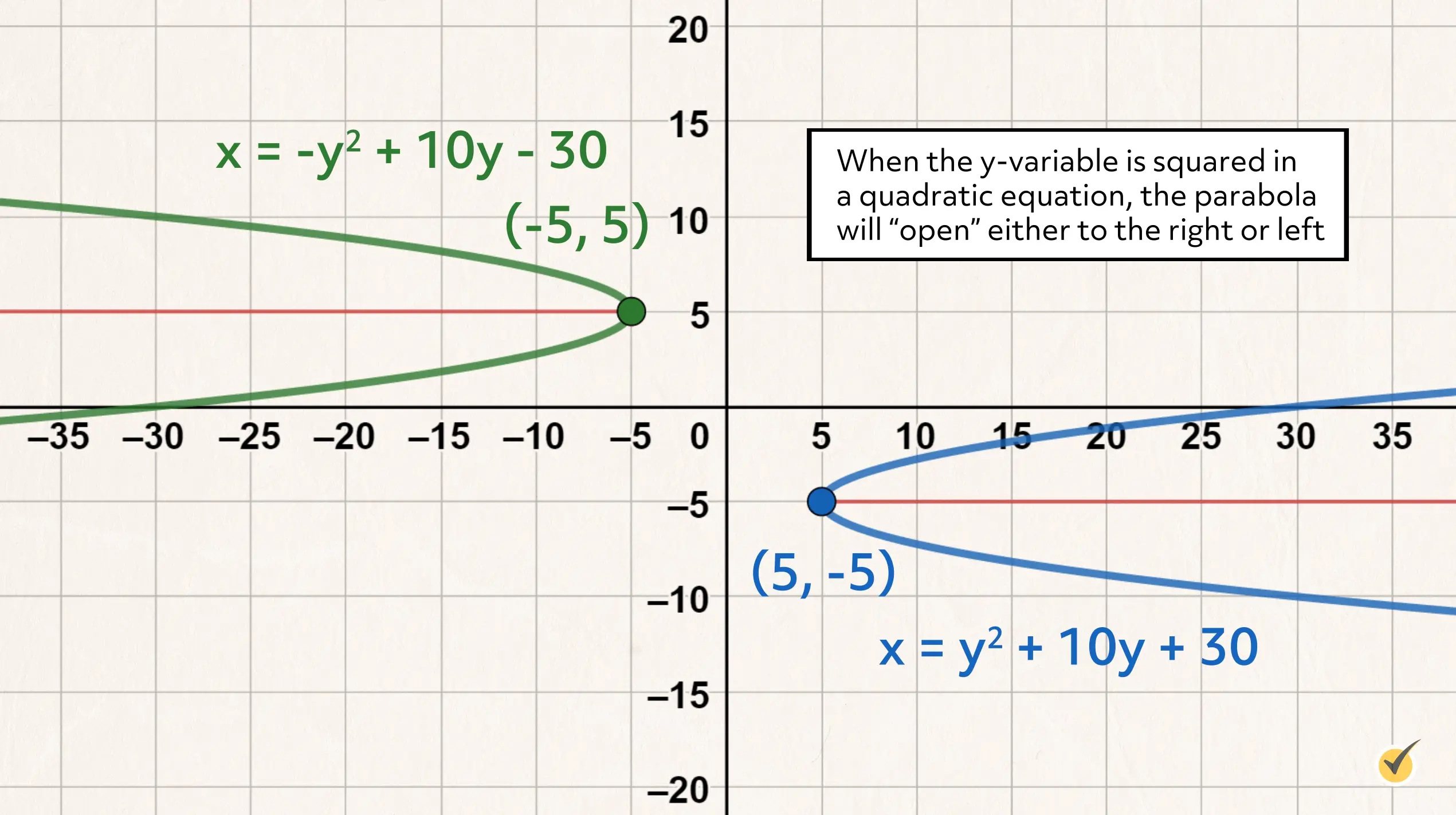
Writing Quadratic Equations
To understand this further, we need to look at how quadratic equations are written. They are written using two basic forms:
- 1. A standard form quadratic equation is written as \(y=ax^2+bx+c\), where \(a\) represents the coefficient of the squared variable, \(b\) is the coefficient of the linear term, and \(c\) represents a constant. Because the \(x\)-variable is squared, this is a quadratic function, which opens either up or down.
A quadratic equation in this form with the \(y\)-variable squared would be written as, \(x=ay^2+by+c\). The parabola graphed from this relation would open either left or right.
- 2. A quadratic that is in vertex form is written as \(y=a(x-h)^2+k\), where \(a\) is the coefficient of a squared binomial which, in this example, contains the \(x\)-variable. The vertex of the parabola is at the ordered pair \((h,k)\). If graphed, this parabola would open either up or down. The equation for a left or right opening parabola in vertex form would be written as \(x=a(y-k)^2+h\).
As you can see, the \(a\)-value is a common element in both forms of the quadratic equation. This value holds the key to which direction the parabola will open.
If the \(a\)-value is positive, equations with the \(x\)-variable squared will graph as parabolas that open UP. Equations with the \(y\)-variable squared will graph as parabolas that open RIGHT.
If the \(a\)-value is negative, equations with the \(x\)-variable squared will graph as parabolas that open DOWN. Equations with the \(y\)-variable squared will graph as parabolas that open LEFT.
Quadratic Equation Examples
To put all of this information together, let’s look at a few examples of quadratic equations:
- 1. \(y=2x^2+3x-6\)
This is a standard form quadratic equation with the \(x\)-variable squared and \(a=2\). Because \(a\gt 0\), the parabola will open “up.”
- 2. \(y=-4(x-3)^2+2\)
This is a vertex form quadratic equation with the \(x\)-variable squared, vertex at the ordered pair \((3,2)\) and \(a=-4\). Because \(a\lt 0\), the parabola will open “down.”
- 3. \(x=3y^2-2y-1\)
This is a standard form quadratic equation with the \(y\)-variable squared and \(a=3\). Because \(a\gt 0\), the parabola will open “right.”
- 4. \(x=-(y-2)^2+1\)
This is a vertex form quadratic with the \(y\)-variable squared, vertex at the ordered pair \((1,2)\), and \(a=-1\). Because \(a\lt 0\), the parabola will open “left.”
Thanks for watching this review of parabolas! I hope it was helpful. See you next time!
Parabola Practice Questions
What is the vertex of the parabola \(y=3(x–4)^2+9\)?
Since the equation of the parabola is in vertex form, \(y=a(x–h)^2+k\), and we know the vertex is \((h,k)\), then the vertex of the parabola is \((4,9)\).
What is the vertex of the parabola \(x=4(y–6)^2–5\)?
The equation of the parabola is given in vertex form, \(x=a(y–k)^2+h\), and the vertex is \((h,k)\). Therefore, the vertex of this parabola is \((-5,6)\).
Which direction does the graph of the parabola \(y=2x^2–5x–3\) open?
The coefficient of the \(x^2\) term determines the direction the parabola opens, in this case, since the coefficient is a positive 2 and the equation of the parabola is in terms of y, then the parabola opens in the upward direction.
Which direction does the graph of the parabola \(x=-y²+y+1\) open?
The equation of the parabola is in terms of x and the coefficient of \(y^2\) is -1, which are the two pieces of information needed to determine which direction the parabola opens. The fact that the equation is in terms of x tells us the parabola is sideways and the -1 tells us it opens to the left.
What is the vertex of the parabola \(y=x^2–2x–5\)?
Since the equation of the parabola is not given in vertex form, we can either graph the equation or change it to vertex form to find the vertex. The graph of the equation shows the vertex is the point located at \((1,-6)\).
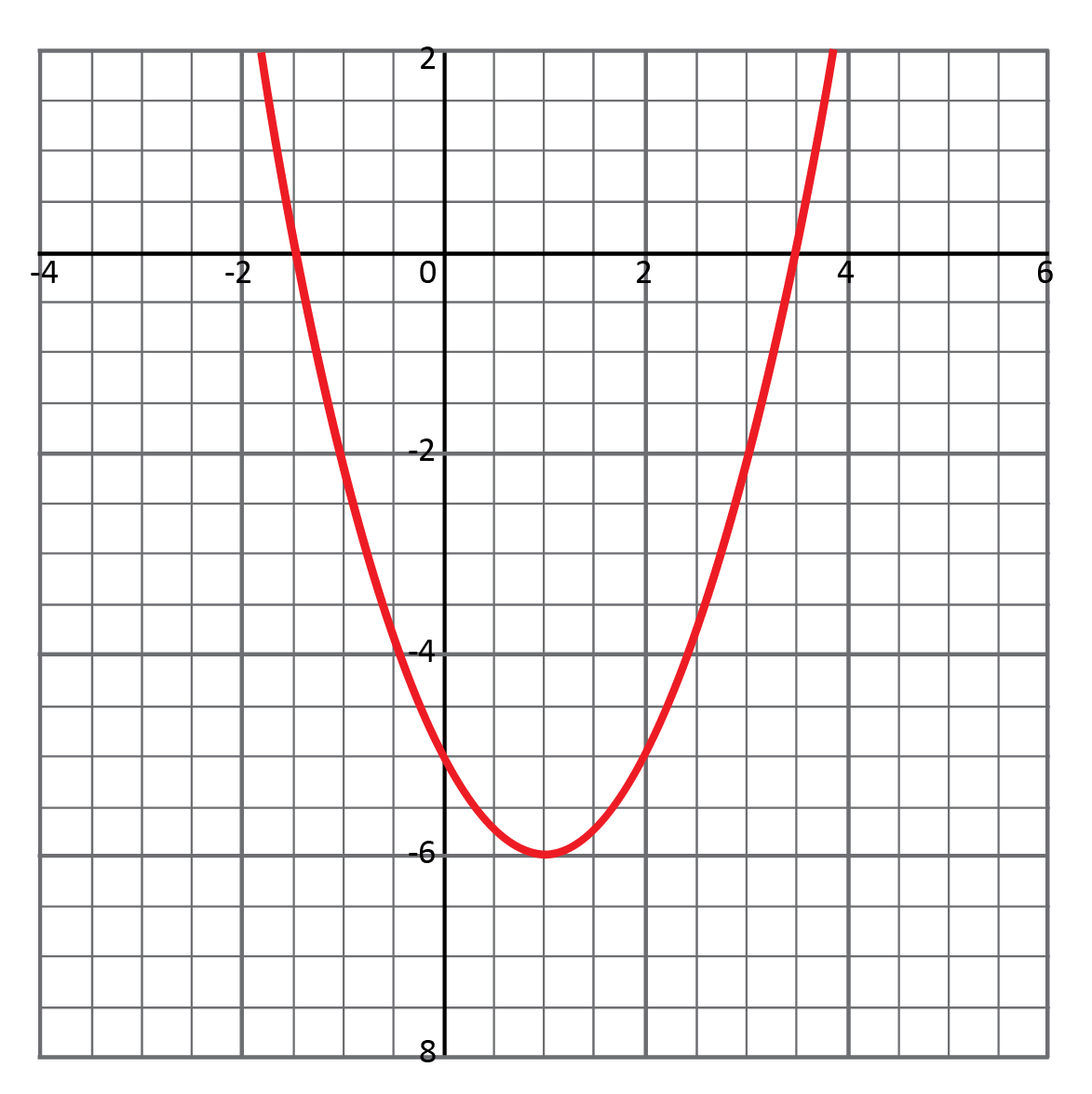
To change the equation into vertex form, we first move the constant to the other side of the equation then ask what coefficient would give us a perfect square? Do not forget, you cannot add something to one side without also adding to the other side. Once we simplify, we can see the equation is now in vertex form and the vertex is \((1,-6)\).
\(y=x^2–2x–5\)
\(y+5+1=x^2–2x+1\)
\(y+6=(x–1)^2\)
\(y=(x–1)^2–6\)
