Hi, and welcome to this video about the domain and range of quadratic functions! In this video, we will explore how the structure of quadratic functions defines their domains and ranges and how to determine the domain and range of a quadratic function.
Let’s get started!
Domain and Range
Before we begin, let’s quickly revisit the terms domain and range.
Domain of a Quadratic Function
The domain of a function is the set of all possible inputs.
Range of a Quadratic Function
The range of a function is the set of all possible outputs.
Structure of a Function
The structure of a function determines its domain and range. Some functions, such as linear functions (e.g., \(f(x)=2x+1\)), have domains and ranges of all real numbers because any number can be input and a unique output can always be produced. On the other hand, functions with restrictions such as fractions or square roots may have limited domains and ranges (e.g., \(f(x)=\frac{1}{2x}\); \(x\neq 0\) because the denominator of a fraction cannot be 0).
Let’s see how the structure of quadratic functions defines and helps us determine their domains and ranges.
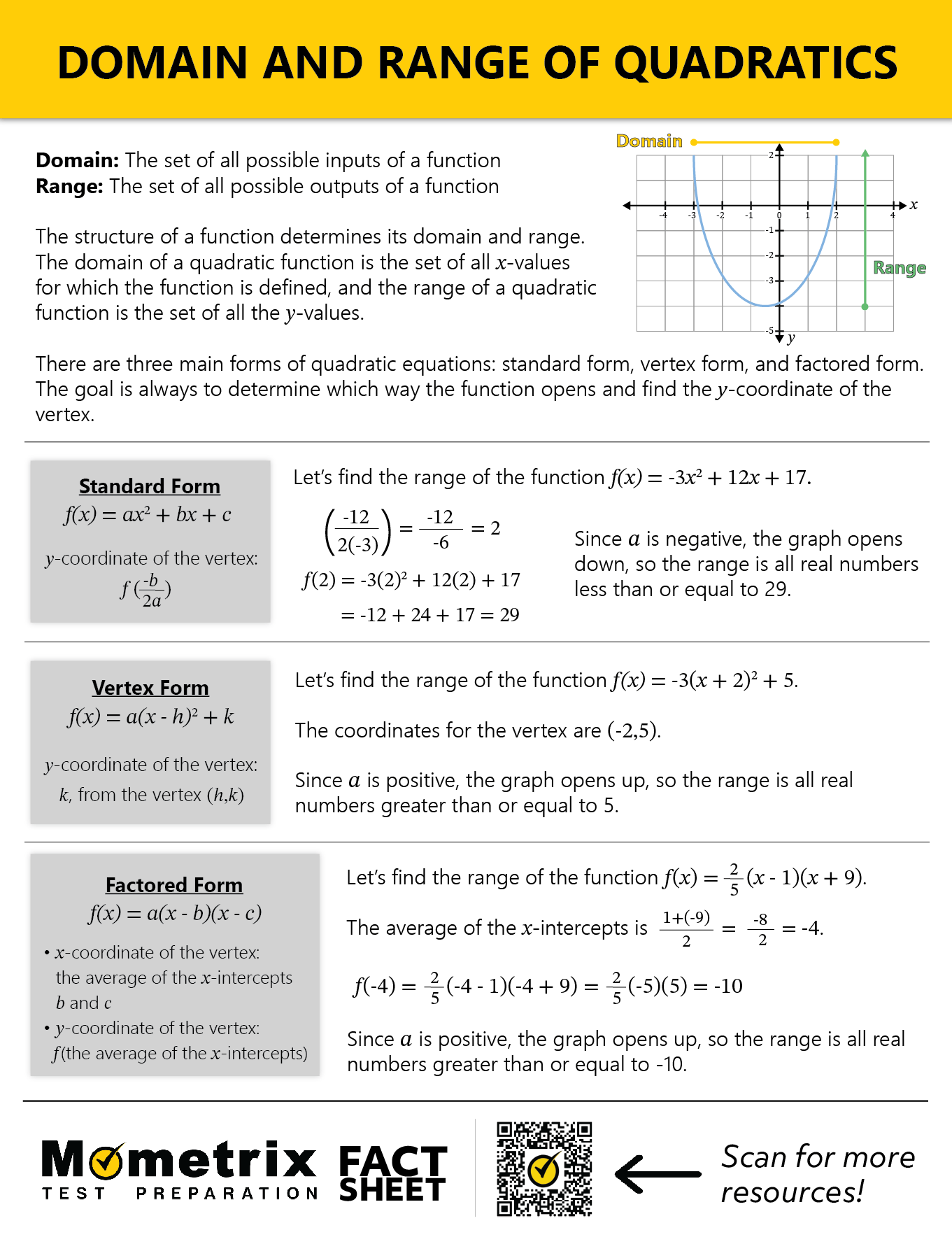
Here’s the graph of \(f(x)=x^{2}\).
Quadratic functions together can be called a family, and this particular function the parent, because this is the most basic quadratic function (i.e., not transformed in any way). We can use this function to begin generalizing domains and ranges of quadratic functions.
To determine the domain and range of any function on a graph, the general idea is to assume that they are both real numbers, then look for places where no values exist.
How to Find the Domain of a Quadratic Function
Let’s talk about domain first. Since domain is about inputs, we are only concerned with what the graph looks like horizontally. To see the domain, let’s move from left-to-right along the \(x\)-axis looking for places where the graph doesn’t exist.
As you can see, there are no places where the graph doesn’t exist horizontally. The domain of this function is all real numbers. In fact, the domain of all quadratic functions is all real numbers!
How to Find the Range of a Quadratic Function
Now for the range. We’ll use a similar approach, but now we are only concerned with what the graph looks like vertically.
As you can see, outputs only exist for \(y\)-values that are greater than or equal to 0. In other words, there are no outputs below the \(x\)-axis. We would say the range is all real numbers greater than or equal to 0.
Let’s generalize our findings with a few more graphs.
The range for this graph is all real numbers greater than or equal to 2.
The range here is all real numbers less than or equal to 5.
The range for this one is all real numbers less than or equal to -2.
And the range for this graph is all real numbers greater than or equal to -3.
As you can see, the turning point, or vertex, is part of what determines the range. The other is the direction the parabola opens. If a quadratic function opens up, then the range is all real numbers greater than or equal to the \(y\)-coordinate of the range. If a quadratic function opens down, then the range is all real numbers less than or equal to the \(y\)-coordinate of the range.
Graphs can be helpful, but we often need algebra to determine the range of quadratic functions. Sometimes, we are only given an equation and other times the graph is not precise enough to be able to accurately read the range.
Using Algebra to Find Domain and Range
So let’s look at finding the domain and range algebraically. There are three main forms of quadratic equations. Our goals here are to determine which way the function opens and find the \(y\)-coordinate of the vertex.
Standard Form
When the quadratic functions are in standard form, they generally look like this:
If \(a\) is positive, the function opens up; if it’s negative, the function opens down. In this form, the \(y\)-coordinate of the vertex is found by evaluating \(f(\frac{-b}{2a})\). For example, consider this function:
\(fx=-2x^2+8x-3\)
So we’re gonna do: \(\frac{-b}{2a}=\frac{-8}{2(-2)}=\frac{-8}{-4}=2\)
Then, we plug this in: \(f(2)=-2(2)^{2}+8(2)-3=-8+16-3=5\)
\(a\) is negative, so the range is all real numbers less than or equal to 5.
Vertex Form
When quadratic equations are in vertex form, they generally look like this:
As with standard form, if \(a\) is positive, the function opens up; if it’s negative, the function opens down. The vertex is given by the coordinates \((h,k)\), so all we need to consider is the \(k\). For example, consider the function \(f(x)=3(x+4)^2-6\). \(a\) is positive and the vertex is at \((-4,-6)\), so the range is all real numbers greater than or equal to \(-6\).
Factored Form
Sometimes quadratic functions are defined using factored form as a way to easily identify their roots. For example:
As with other forms, if \(a\) is positive, the function opens up; if it’s negative, the function opens down. One way to use this form is to multiply the terms to get an equation in standard form, then apply the first method we saw. We can also apply the fact that quadratic functions are symmetric to find the vertex. We know the roots, and therefore, the locations of the \(x\)-intercepts. Horizontally, the vertex is halfway between them.
Once we know the location of the vertex—the \(x\)-coordinate—all we need to do is substitute into the function to find the \(y\)-coordinate. For example, consider the function \(f(x)=-2(x+4)(x-2)\). The \(x\)-intercepts are at \(-4\) and \(+2\), and the vertex is located at \(\frac{-4+2}{2}=-1\) (simply take the “average” of the \(x\)-intercepts). And we’re going to plug that into our original equation, so we have: \(f(-1)=-2(-1+4)(-1-2)=-2(3)(-3)=18\). Since \(a\) is negative, the range of all real numbers is less than or equal to 18.
Review
Ok, let’s do a quick review before we go.
- Domain is the set of input values, while range is the set of output values.
- To determine the domain and range of any function on a graph, the general idea is to assume that they are both real numbers, then look for places where no values exist.
- And finally, when looking at things algebraically, we have three forms of quadratic equations: standard form, vertex form, and factored form.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is the range of a quadratic function?
A
The range of a quadratic function is a list of all the possible \(y\)-values of a quadratic function.
Q
How do you find the domain of a quadratic function?
A
The domain of a quadratic function is always \((-∞,∞)\) because quadratic functions always extend forever in either direction along the \(x\)-axis.
Q
What makes the function quadratic?
A
A function is considered quadratic if it has a degree of 2. In other words, a function is quadratic if it has an \(x^2\)-term.
Q
Can a quadratic function have a range of \((-∞,∞)\)?
A
No, a quadratic function cannot have a range of \((-∞,∞)\). In order for this to happen, the parabola would have to be on its side, like this: 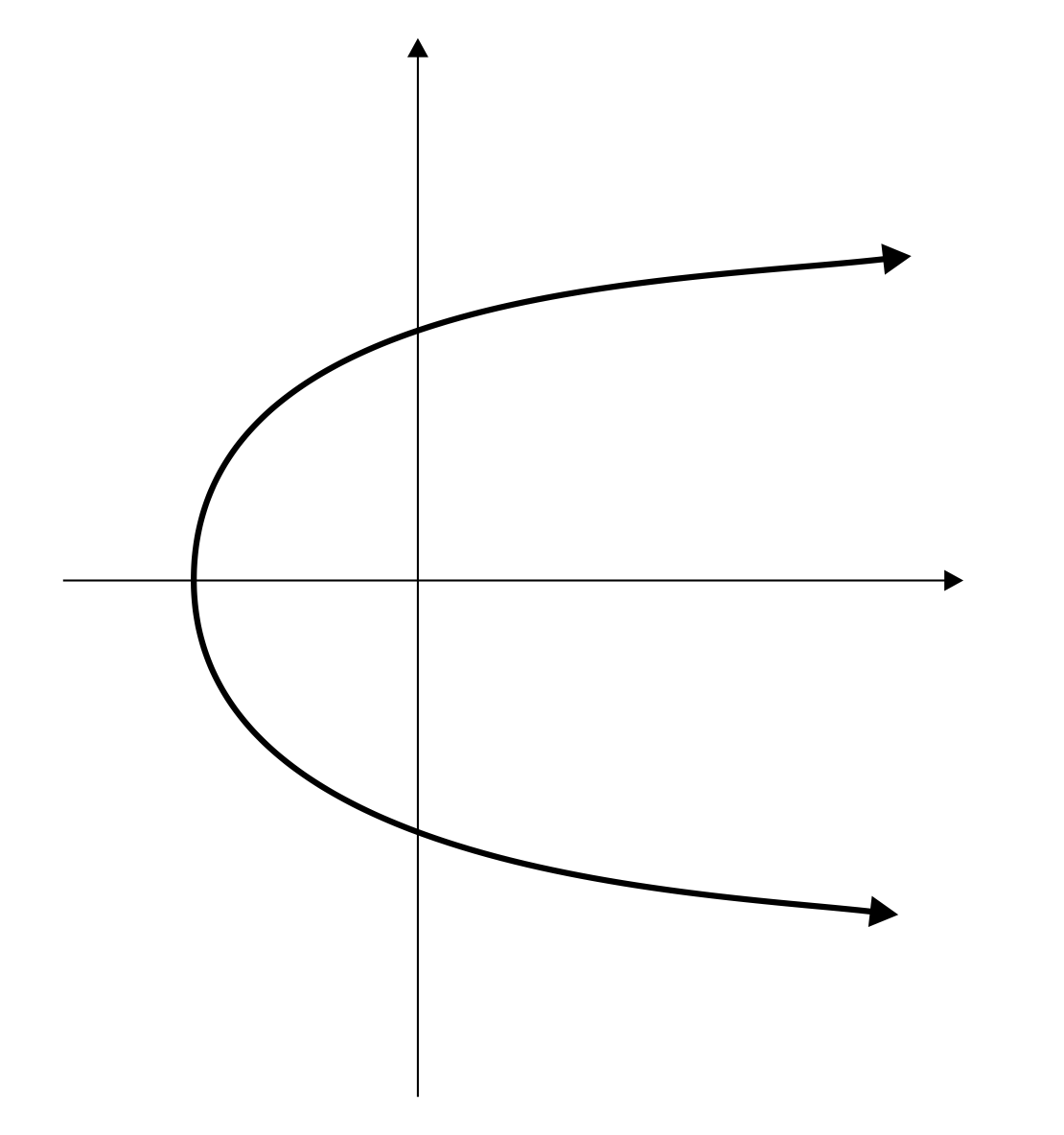
However, if this were to happen, it would not be considered a function because the graph fails the vertical line test.
Q
How do you find the range of a quadratic function?
A
To find the range of a standard quadratic function in the form \(f(x)=ax^2+bx+c\), find the vertex of the parabola and determine if the parabola opens up or down. To find the vertex of a quadratic in this form, use the formula \(x=-\frac{b}{2a}\). This will give you the \(x\)-coordinate of the vertex, and the \(y\)-coordinate can be found by plugging this \(x\)-value into the original equation and solving for \(f(x)\) (or \(y\)). Next, determine if the parabola opens up or down. If the value of \(a\) is positive, then the parabola opens up and the range is \((y\)-coordinate of the vertex, \(∞)\). If the value of \(a\) is negative, then the parabola opens down and the range is \((-∞, y\)-coordinate of the vertex\()\).
Here’s an example: What is the range of \(y=2x^2+4x-5\)?
- Find the \(x\)-coordinate of the vertex: \(x=-\frac{b}{2a}=-\frac{4}{2(2)}=-1\)
- Find the \(y\)-coordinate of the vertex: \(y=2x^2+4x-5=2(-1)^2+4(-1)-5=-7\)
- Determine if the parabola opens up or down: up, because \(a=2\) and 2 is positive
Therefore, the range of \(y=2x^2+4x-5\) is \((-7,∞)\).
Quadratic Function Domain and Range PDF
Domain and Range of Quadratic Functions Practice Questions
Find the domain and range of the equation \(f(x)=3x^2+6x-2\).
The domain of this function is all real numbers because there is no limit on the values that can be plugged in for \(x\). However, there are limits to the output values. To find the possible output values, or the range, two things must be known: 1) if the graph opens up or down, and 2) what the \(y\)-value of the vertex is. This equation is in standard form, and \(a\) is positive, which indicates that the graph opens up. This means the range will be greater than or equal to some value. Here’s how to find that value:
First, evaluate \(f(\frac{-b}{2a})\).
\(f(\frac{-6}{2(3)})\)
\(f(\frac{-6}{6})\)
\(f(-1)\)
Now, plug this back into the original equation.
\(f(x)=3x^2+6x-2\)
\(f(-1)=3(-1)^2+6(-1)-2\)
\(f(-1)=3-6-2\)
\(f(-1)=-5\)
Since \(a\) is positive, we know that the range is all real numbers greater than or equal to -5.
Find the domain and range of the equation \(f(x)=-3x^2+6x-3\).
The domain of this function is all real numbers because there is no limit on the values that can be plugged in for \(x\). However, there are limits to the output values. To find the possible output values, or the range, two things must be known: 1) if the graph opens up or down, and 2) what the \(y\)-value of the vertex is. This equation is in standard form, and \(a\) is negative, which indicates that the graph opens down. This means the range will be less than or equal to some value.
Here’s how to find that value:
First, evaluate \(f(\frac{-b}{2a})\).
\(f(\frac{-6}{2(-3)})\)
\(f(\frac{-6}{-6})\)
\(f(1)\)
Now, plug this back into the original equation.
\(f(x)=-3x^2+6x-3\)
\(f(1)=-3(1)^2+6(1)-3\)
\(f(1)=-3+6-3\)
\(f(1)=0\)
Since \(a\) is negative, the range is all real numbers less than or equal to zero.
Find the domain and range of the equation \(f(x)=2(x+3)^2-8\).
This equation is in vertex form: \(f(x)=a(x-h)^2+k\).
The domain, or values for \(x\), can be any real number, but the range does have restrictions. Not all \(y\)-values will appear on the graph for this equation. To find the range, first find the vertex, which is located at (\(h\), \(k\)). Referring back to the original equation shows that (\(h\), \(k\)) would be \((-3,-8)\). Since \(a\) is positive, the range is all real numbers greater than or equal to -8.
Find the domain and range of the equation \(f(x)=4(x+7)^2+5\).
This equation is in vertex form. The domain, or values for \(x\), can be any real number, but the range does have restrictions. Not all \(y\)-values will appear on the graph for this equation. To find the range, first find the vertex, which is located at (\(h\), \(k\)). Referring back to the original equation shows that (\(h\), \(k\)) would be \((-7,5)\). Since \(a\) is positive, the range is all real numbers greater than or equal to 5.
Find the domain and range of the equation \(y=-4(x+4)(x-6)\).
This equation is in a factored form. The domain is all real numbers because there is no restriction for the value of \(x\), or the input. Because the equation is in a factored form, the \(x\)-intercepts can be identified easily. The equation \(f(x)=-4(x+4)(x-6)\) shows that the \(x\)-intercepts are at -4 and 6. These two values can be averaged in order to find the vertex, or \(y\)-intercept. Average -4 and 6 to get \(\frac{-4+6}{2}\), which simplifies to 1. Now, take this value and plug it into the original equation: \(f(1)=-4(1+4)(1-6)\), which simplifies to 100. In the original equation, \(a\) was negative, so the range is all real numbers less than or equal to 100.