
Hi, and welcome to this video about finding the area of composite shapes made of rectangles and semicircles.
Many geometric shapes have their very own formulas for finding their areas. But other shapes don’t have common names or formulas. Today we’ll find the area for a couple of those shapes. We’ll even create a formula for one of them just for fun and then not use it.
Example #1
Here’s our shape:
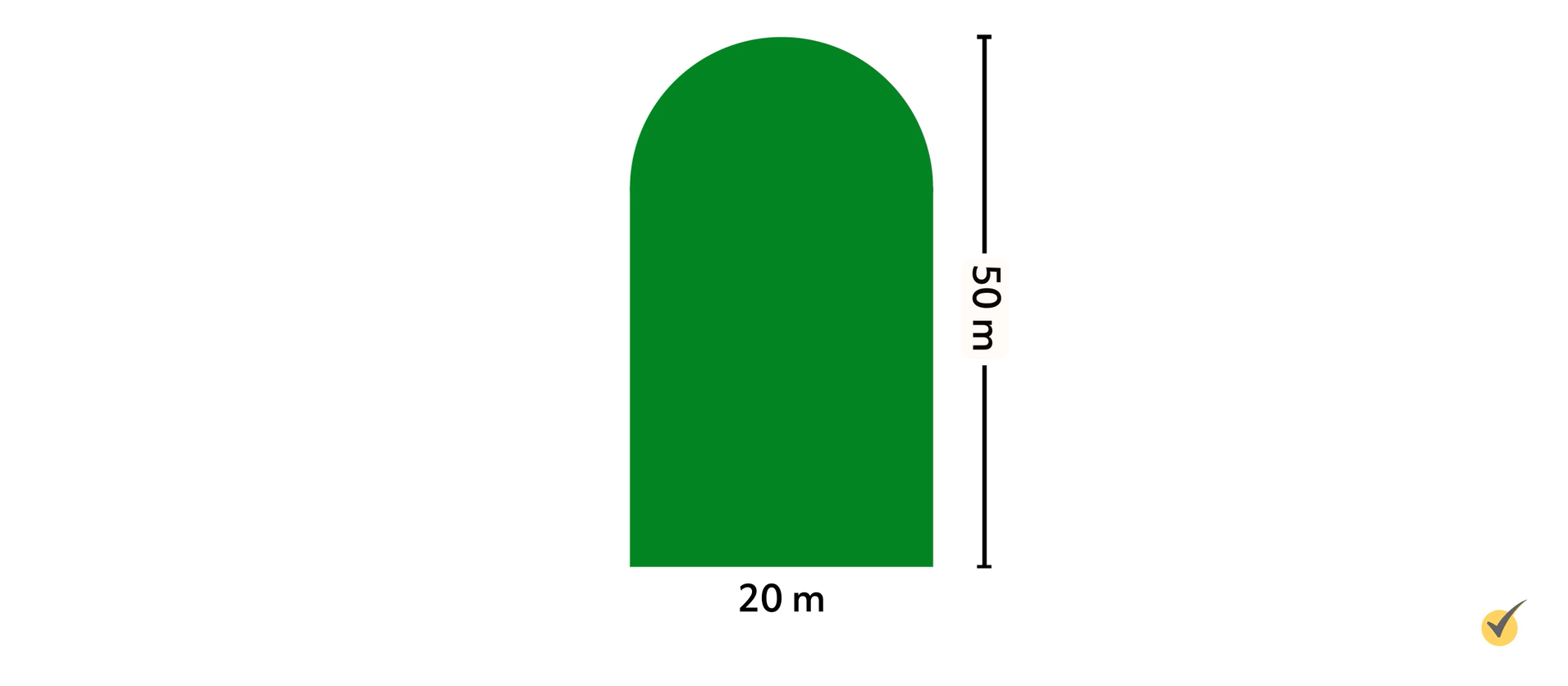
It’s a classic “tombstone” shape. It’s a composite shape, which means it’s made up of two or more simpler shapes. This one is made up of a rectangle and a semicircle, which is half a circle, as we can see here:
To find the area of this shape, we need to find the area of the rectangle at the bottom and the area of the semicircle at the top and then simply add the two together to get our total area. But first we need to review the formulas used to find the areas of rectangles and circles.
In this case, we only have half of a circle, so we need to modify our circle formula a bit. Dividing by 2 will make it the area of a semicircle:
Now we can create the formula for the area of our “tombstone” shape:
It’s just the area of the rectangle plus the area of the semicircle. In truth, we don’t really need the formula. Logic dictates that we’re going to add the pieces of this composite shape to get our total area anyway.
Example #2
Let’s try a problem:
We can see that our shape is \(50\) meters tall and \(20\) meters wide. This is the typical information given for this type of problem. What makes this tricky is that we know the width of the shape, which is the width of the rectangle, but we don’t know the radius of the circle or the length of the rectangle. Uh-oh!
Looking at our diagram, though, we see that we could draw another radius that is horizontal.
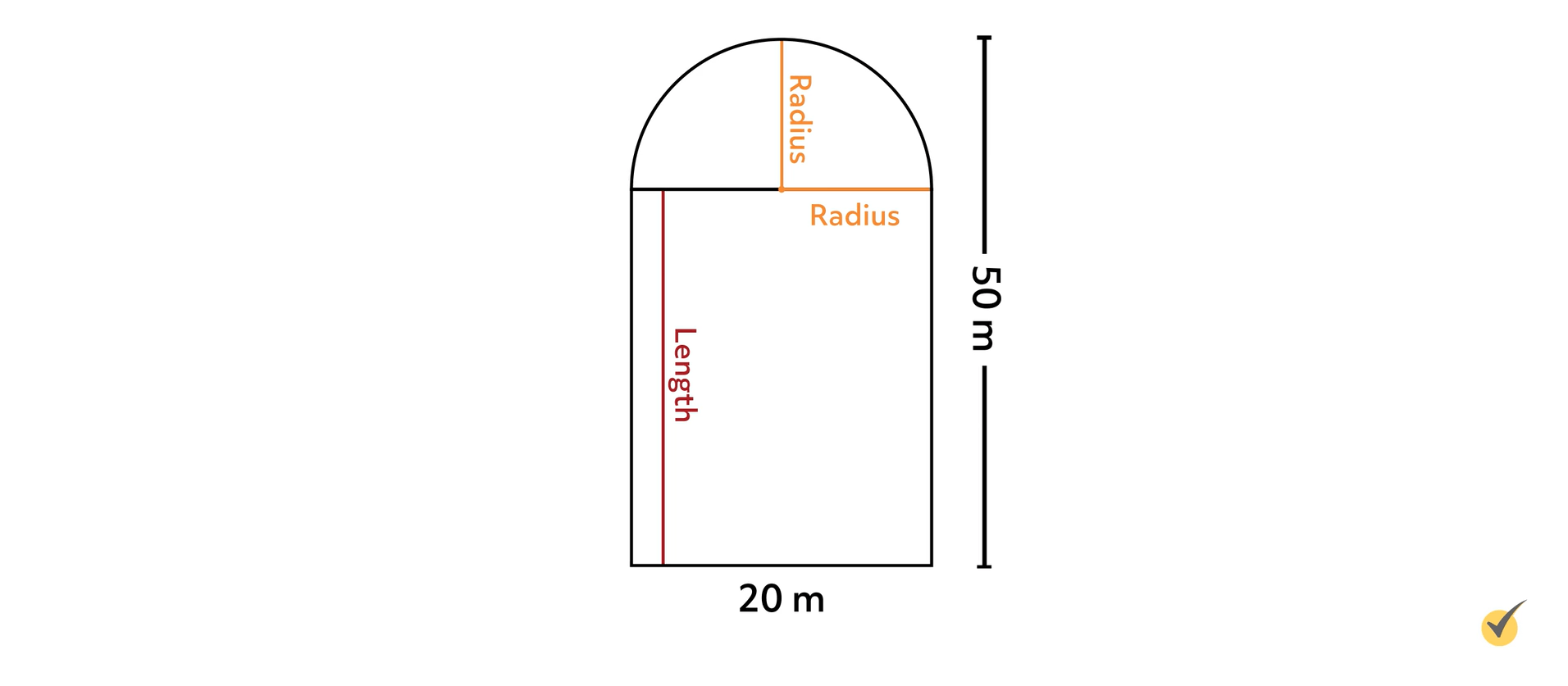
Now we can see that this radius is half the width of our shape! And since we know that the width of our shape is \(20\) meters, we can find the radius by dividing that by \(2\)! So our radius is \(10\) meters!
Now we can not only find the area of the semicircle, but we can also find the length of the rectangle! Since the height of our object is \(50\) meters and the height of the semicircle part, our radius, is \(10\) meters, that means the length of our rectangle is \(50\) meters-\(10\) meters, which is \(40\) meters! Now we have all the information we need:
\(l=40\text{ m}\)
\(w=20\text{ m}\)
Let’s find the area of our semicircle first:
\(A=\frac{π(10 m)^2}{2}\)
\(A=\frac{100π m^2}{2}\)
\(A=50π\text{ m}^2\)
The area of our semicircle is \(50\) pi meters squared. That’s the exact area. We could use \(3.14\) as an approximation for pi and multiply by \(50\) to get an approximate area that could be a bit more useful for a real world problem, but first, let’s find the area of our rectangle.
\(A=(40\text{m})(20\text{m})\)
\(A=800\text{m}^2\)
Now that we know the area of both objects that make up our composite shape, we can add them together to get our total area.
To get a more useful approximate value, we can multiply \(50\) by an approximation of pi using the key on our calculator to get an approximate area of \(157.08\) meters squared.
m^2\)
\(+157.08 m^2\approx{957.08} m^2\)
Notice that we used the “approximately equal to” symbol \(( \approx)\) since our semicircle area is now an approximation.
Example #3
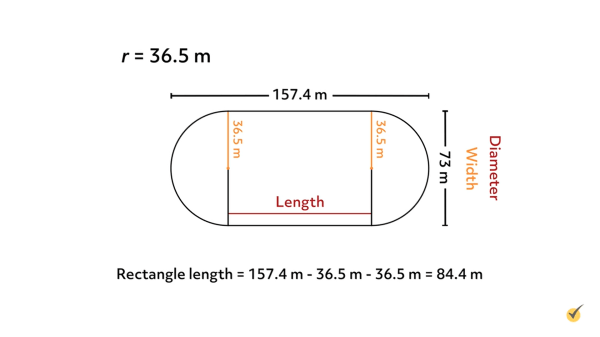
For our next problem, let’s try to find the area for another related shape, the stadium:
It’s not hard to see where it gets its name! It’s shaped like a track and field stadium. For a real world problem, let’s calculate the area of an outdoor track and field stadium.
Just like with our “tombstone”-shaped problem, problems of this type only give two dimensions of our shape – the total width and the total length.
But that’s all the information that we need! As we saw in the last problem, our width is also the diameter of our circle:
That means that we can find the radius by simply dividing our diameter by \(2\). Here the width, or the diameter, is \(73\) meters, so our radius is \(36.5\) meters. That’s one piece of the puzzle completed. Now we just need to find the length of the rectangle.
The total length of our stadium infield is \(157.4\) meters, but we need to subtract the length of each semicircle from that. So we subtract the radius of the left semicircle and the right semicircle:
\(-36.5\text{ meters}=84.4\text{ meters}\)
Now we have all of the information we need to find our total area.
\(l=84.4\text{ m}\)
\(w=73\text{ m}\)
Before we begin calculating, let’s take another look at our stadium. Notice that there are two semicircles. If we removed the rectangle between them and pushed them together, we’d have a complete circle! So to find the area of both semicircle ends at once, we can just use the formula for the area of a whole circle:
\(A=π(36.5\text{ m})^{2}\)
\(A=1,332.25π\text{ m}^2\)
The area of our two semicircles together is \(1,332.25π\text{ m}^2\). Remember, that’s the exact area. We’ll find the approximate total area after we find our rectangle’s area.
\(A=(84.4\text{ m})(73\text{ m})^2\)
\(A=6,161.2\text{ m}^2\)
Now that we know the area of the parts that make up our stadium shape we simply add them together:
\(+1,332.25π\text{ m}^2\)
While exact, this answer wouldn’t be decipherable by most people. So it makes sense to write it as an approximation. We find the approximate area of our two semicircles by multiplying \(1,332.25\) by π on our calculators to find \(4,185.39\text{ m}^2\).
\(+4,185.39\text{ m}^2\approx 10,346.6\text{ m}^2\)
Once again, we use the “approximately equal to” symbol because our semicircle areas are now an approximation.
That’s it for finding the area of composite shapes made of circles and rectangles. Thanks for watching, and happy studying!
Area of Composite Shape Practice Questions
Calculate the area of the compound figure. Use 3.14 for \(\pi\).
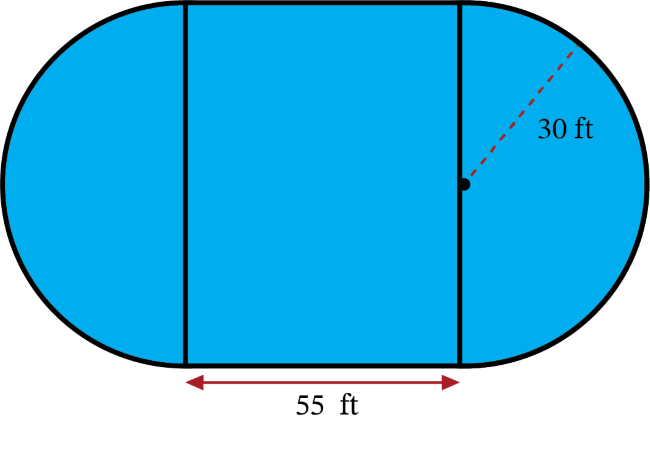
Calculate the area of the rectangle: \(A=l\times w\) becomes \(A=55\text{ ft}\times60\text{ ft}\), which simplifies to \(A=3{,}300\text{ ft}^2\).
Calculate the area of the two semicircles (one circle): \(A=\pi r^2\) becomes \(A=(3.14)(30)^2\), which simplifies to \(A=2{,}826\text{ ft}^2\).
Add the two areas together: \(3{,}300\text{ ft}^2+2{,}826\text{ ft}^2=6{,}126\text{ ft}^2\)
The shape below is made up of a semicircle and a square. The radius of the semicircle is 5 cm. What is the area of the entire figure? Use 3.14 for \(\pi\).
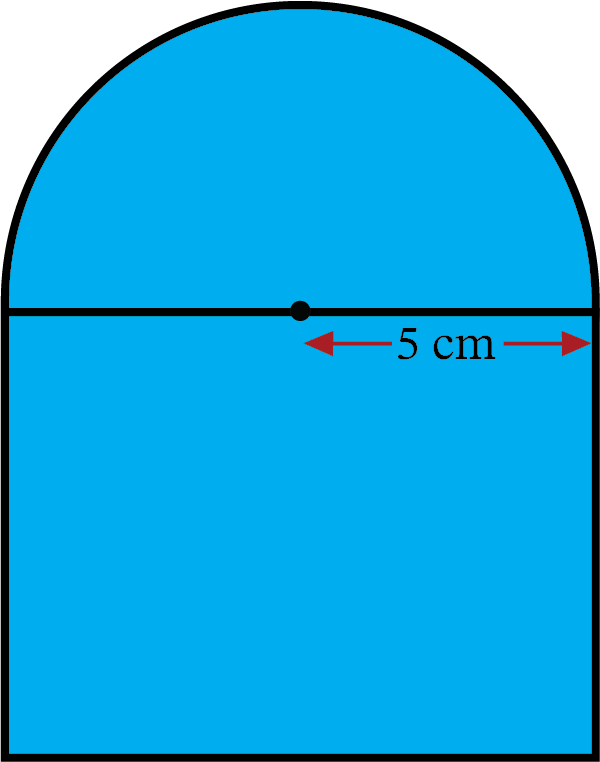
Add the area of the square to the area of the semicircle.
Each side of the square has length \(2\times5\text{ cm}=10\text{ cm}\). The area of the square is \(10\text{ cm} \times\ 10\text{ cm}\), which equals \(100\text{ cm}^2\).
The area of the semicircle is \(\frac{\pi r^2}{2}\). \(\frac{\pi r^2}{2}\) becomes \(\frac{(3.14){(5)}^2}{2}\), which simplifies to \(39.25\text{ cm}^2\).
Add the two areas: \(100\text{ cm}^2+39.25\text{ cm}^2=139.25\text{ cm}^2.\)
Calculate the surface area of the image below. Round your answer to the nearest whole number. Use 3.14 for \(\pi\).
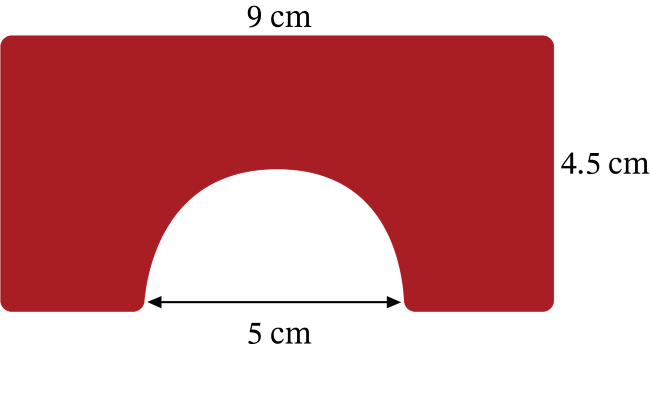
Subtract the area of the semicircle from the area of the rectangle. The area of the rectangle is found using the formula \(A=l\times w\). In this case, \(A=9\times\ 4.5\), which simplifies to \(A=40.5\). The area of the rectangle is \(40.5\text{ cm}^2\).
Now find the area of the semicircle using the formula \(A=\frac{\pi r^2}{2}\). In this case, \(A=\frac{(3.14)({2.5)}^2}{2}\), which simplifies to \(A=9.8125\).
Now subtract this from the rectangle’s area.
\(40.5-9.8125=30.6875\)
Rounded to the nearest whole number, the shape’s area is \(31\text{ cm}^2\).
A landscaper is designing a backyard with a pool for a client. The pool will be surrounded by grass. How much grass will be planted? Use 3.14 for \(\pi\).
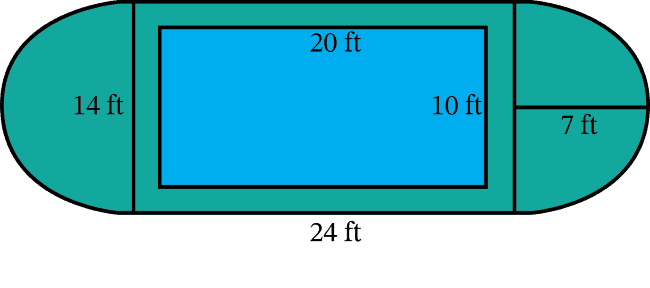
The two semicircles on either end make a circle. Find the area of the circle. Add this to the large green rectangle. Then subtract the blue rectangle.
The area of the circle (two semicircles) is calculated as \(\pi r^2\). \(\pi r^2\) becomes \((3.14)(7)^2\), which simplifies to \(153.86\text{ ft}^2\).
Now calculate the area of the large green rectangle. \(24\text{ ft} \times 14\text{ ft}=336\text{ ft}^2\). Add this to the green circle.
\(153.86\text{ ft}^2+336\text{ ft}^2=489.86\text{ ft}^2\)
Now subtract the blue rectangle from this. The blue rectangle (swimming pool) measures \(20\text{ ft} \times\ 10\text{ ft}=200\text{ ft}^2\).
\(489.86\text{ ft}^2-200\text{ ft}^2=289.86\text{ ft}^2\)
Antonio wants to use chalk to draw a basketball court on his driveway similar to the image. He wants the rectangle to be 18 ft by 6 ft. The semicircle at the top of the rectangle will have a radius of 3 ft. What is the surface area of the yellow region of the court? Use 3.14 for \(\pi\), and round your answer to the nearest whole number.
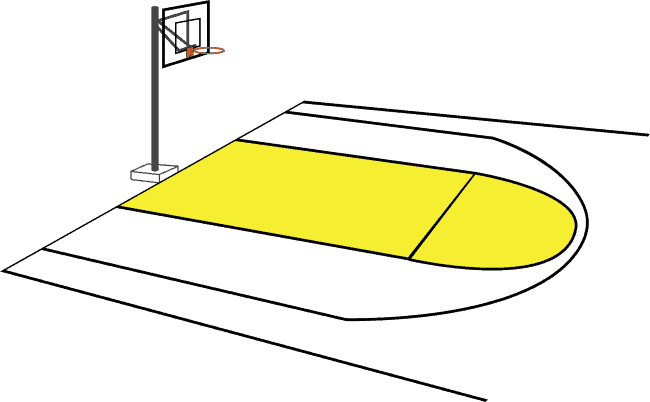
Add the area of the rectangle to the area of the semicircle. The area of the rectangle is found using the formula \(A=l\times w\). The area of the semicircle is found using the formula \(A=\frac{\pi r^2}{2}\).
Rectangle: \(A=l\times w\) becomes \(A=18\times6\), which simplifies to \(A=108\text{ ft}^2\).
Semicircle: \(A=\frac{\pi r^2}{2}\) becomes \(A=\frac{(3.14)(3)^2}{2}\), which simplifies to \(A=14.13\text{ ft}^2\).
Now add the two areas.
\(108\text{ ft}^2+14.13\text{ ft}^2=122.13\text{ ft}^2\)
When \(122.13\text{ ft}^2\) is rounded to the nearest whole number we get \(122\text{ ft}^2\).