
Hello, and welcome to this video about rotation! In this video, we will explore the rotation of a figure about a point. Let’s learn about rotations!
What is Rotation?
Rotations are everywhere you look. The earth is the most common example, rotating about an axis. The wheel on a car or a bicycle rotates about the center bolt. These two examples rotate 360°. There are other forms of rotation that are less than a full 360° rotation, like a character or an object being rotated in a video game.
Rotation in Math
More formally speaking, a rotation is a form of transformation that turns a figure about a point. We call this point the center of rotation. A figure and its rotation maintain the same shape and size but will be facing a different direction. A figure can be rotated clockwise or counterclockwise. Another great example of rotation in real life is a Ferris Wheel where the center hub is the center of rotation.
Angle of Rotation
The measure of the amount a figure is rotated about the center of rotation is called the angle of rotation. The angle of rotation is usually measured in degrees. We specify the degree measure and direction of a rotation. Here is a figure rotated 90° clockwise and counterclockwise about a center point.
Using a Coordinate Grid for Rotations
A great math tool that we use to show rotations is the coordinate grid.
Let’s start by looking at rotating a point about the center \((0,0)\). If you take a coordinate grid and plot a point, then rotate the paper 90° or 180° clockwise or counterclockwise about the origin, you can find the location of the rotated point. Let’s look at a real example. Here, we plotted point A at \((5,6)\) then we rotated the paper 90° clockwise to create point A’, which is at \((6,-5)\).
Here is the same point A at \((5,6)\) rotated 180° counterclockwise about the origin to get \(A’(-5,-6)\).
Let’s take a closer look at the two rotations from our experiment. In our first experiment, when we rotate point \(A (5,6)\) 90° clockwise about the origin to create point \(A’ (6,-5)\), the y-value of point A became the x-value of point A’ and the \(x\)-value of point A became the \(y\)-value of point A’ but with the opposite sign.
In our second experiment, point \(A (5,6)\) is rotated 180° counterclockwise about the origin to create \(A’ (-5,-6)\), where the \(x\)– and \(y\)-values are the same as point A but with opposite signs.
Rotation Rules for the Coordinate Grid
Lucky for us, these experiments have allowed mathematicians to come up with rules for the most common rotations on a coordinate grid, assuming the origin, \((0,0)\), as the center of rotation.
Here are the rotation rules:
- 90° clockwise rotation: \((x,y)\) becomes \((y,-x)\)
- 90° counterclockwise rotation: \((x,y)\) becomes \((-y,x)\)
- 180° clockwise and counterclockwise rotation: \((x,y)\) becomes \((-x,-y)\)
- 270° clockwise rotation: \((x,y)\) becomes \((-y,x)\)
- 270° counterclockwise rotation: \((x,y)\) becomes \((y,-x)\)
As you can see, our two experiments follow these rules.
Rotation Examples
Example #1
Now that we know how to rotate a point, let’s look at rotating a figure on the coordinate grid. To rotate triangle ABC about the origin 90° clockwise we would follow the rule (x,y) → (y,-x), where the y-value of the original point becomes the new \(x\)-value and the \(x\)-value of the original point becomes the new \(y\)-value with the opposite sign. Let’s apply the rule to the vertices to create the new triangle A’B’C’:
- \(A (-4,7)\) becomes \(A’ (7,4)\)
- \(B (-6,1)\) becomes \(B’ (1,6)\)
- \(C (-2,1)\) becomes \(C’ (1,2)\)
Example #2
Let’s take a look at another rotation. Let’s rotate triangle ABC 180° about the origin counterclockwise, although, rotating a figure 180° clockwise and counterclockwise uses the same rule, which is \((x,y)\) becomes \((-x,-y)\), where the coordinates of the vertices of the rotated triangle are the coordinates of the original triangle with the opposite sign. Let’s apply the rule to the vertices to create the new triangle A’B’C’:
- \(A (2,7)\) becomes \(A’ (-2,-7)\)
- \(B (2,1)\) becomes \(B’ (-2,-1)\)
- \(C (6,1)\) becomes \(C’ (-6,-1)\)
Example #3
Here is quadrilateral ABCD. To rotate quadrilateral ABCD 90° counterclockwise about the origin we will use the rule \((x,y)\) becomes \((-y,x)\). Let’s apply the rules to the vertices to create quadrilateral A’B’C’D’:
- \(A (-8,-2)\) becomes \(A’ (2,-8)\)
- \(B (-7,-7)\) becomes \(B’ (7,-7)\)
- \(C (-2,-6)\) becomes \(C’ (6,-2)\)
- \(D (-3,-2)\) becomes \(D’ (2,-3)\)
Example #4
Now I want you to try some practice problems on your own. Kite KLMN is shown on the coordinate grid. The kite has been rotated about the origin to create the kite K’L’M’N’. Can you identify which rotation of kite KLMN created kite K’L’M’N’?
Let’s start by identifying the coordinates of the vertices of kite KLMN and of our rotated kite:
- \(K (-8,3)\) becomes \(K’ (8,-3)\)
- \(L (-5,5)\) becomes \(L’ (5,-5)\)
- \(M (-2,3)\) becomes \(M’ (2,-3)\)
- \(N (-5,-3)\) becomes \(N’ (5,3)\)
A closer look at the coordinates of the vertices shows that the coordinates of K’L’M’N’ are the same as the vertices of the original kite but with the opposite sign. Let’s look at the rules, the only rule where the values of the x and y don’t switch but their sign changes is the 180° rotation.
- 90° clockwise rotation: \((x,y)\) becomes \((y,-x)\)
- 90° counterclockwise rotation: \((x,y)\) becomes \((-y,x)\)
- 180° clockwise and counterclockwise rotation: \((x,y)\) becomes \((-x,-y)\)
- 270° clockwise rotation: \((x,y)\) becomes \((-y,x)\)
- 270° counterclockwise rotation: \((x,y)\) becomes \((y,-x)\)
Therefore, kite KLMN was rotated 180° about the origin to create kite K’L’M’N’.
Example #5
Let’s look at another problem. Pentagon QRSTU is shown on the coordinate grid. Rotate pentagon QRSTU 90° counterclockwise to create pentagon Q’R’S’T’U’.
Let’s start by finding the coordinates of the vertices of our original pentagon. The rule for 90° counterclockwise rotation is \((x,y)\) becomes \((-y,x)\), let’s apply the rule to find the vertices of our new pentagon.
- \(Q (-6,6)\) becomes \(Q’ (-6,-6)\)
- \(R (-4,7)\) becomes \(R’ (-7,-4)\)
- \(S (0,4)\) becomes \(S’ (-4,0)\)
- \(T (-4,1)\) becomes \(T’ (-1,-4)\)
- \(U (-6,2)\) becomes \(U’ (-2,-6)\)
Now let’s plot the points on the coordinate grid and label the vertices.
Example #6
One last practice problem. Trapezoid PQRS, where \(P (-3,-5)\), \(Q (3,-5)\), \(R (5,-2)\), and \(S (-5,-2)\) is rotated 90° clockwise about the origin to create trapezoid P’Q’R’S’. Create both trapezoids on the coordinate grid.
We will start by deciding which rule to use for 90° clockwise rotation about the origin. We are going to use \((x,y)\) becomes \((y,-x)\). Now let’s apply the rule to the coordinates of the vertices of PQRS.
- \(P (-3,-5)\) becomes \(P’ (-5,3)\)
- \(Q (3,-5)\) becomes \(Q’ (-5,-3)\)
- \(R (5,-2)\) becomes \(R’ (-2,-5)\)
- \(S (-5,-2)\) becomes \(S’ (-2,5)\)
Now let’s plot the points and create the trapezoids on the coordinate grid.
I hope that this overview of rotation was helpful! Thanks for watching, and happy studying!
Rotation Practice Questions
On the coordinate plane, point \(A (3,-4)\) is rotated 180° in a counterclockwise direction about the origin to create the rotated point A’. Which of the following is the ordered pair for A’?
Rotating a point that has the coordinates \((x,y)\) 180° about the origin in a counterclockwise or clockwise direction produces a point that has the coordinates \((-x,-y)\). Substituting the coordinates for point A into our formula to find the rotated point, we get:
\(A’\left(-3,-\left(-4\right)\right)=A'(-3,\ 4)\)
The coordinates of the vertices for triangle ABC that can be graphed in the coordinate plane are \(A(-8,-6)\), \(B(-2,-6)\), and \(C(-5,-3)\). The triangle is rotated 90° in a clockwise direction about the origin to produce triangle A’B’C’. Which of the following are the vertices for triangle A’B’C’?
Rotating a point that has the coordinates \((x,y)\) 90° about the origin in a clockwise direction produces a point that has the coordinates \((y,-x)\). Substituting the coordinates for our points into our formula to find the rotated points, we get:
\(A’\left(-6,-\left(-8\right)\right)=A’\left(-6,\ 8\right)\)
\(B’\left(-6,-\left(-2\right)\right)=B’\left(-6,\ 2\right)\)
\(C’\left(-3,-\left(-5\right)\right)=C'(-3,\ 5)\)
Thus, the coordinates for the vertices for triangle A’ B’ C’ are \(A’ (-6,8)\), \(B’ (-6,2)\), and \(C’ (-3,5)\).
The graph of quadrilateral ABCD is shown below.
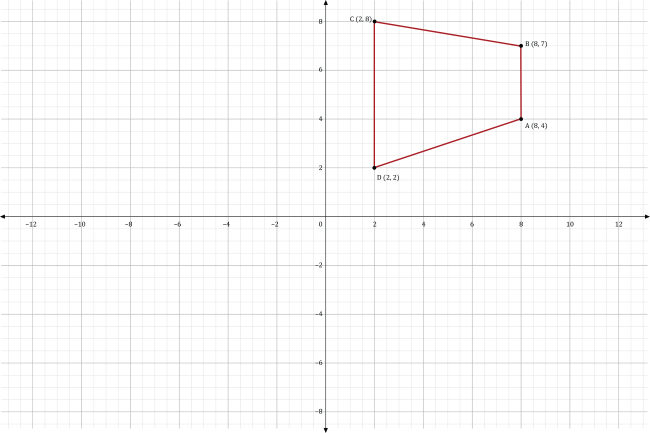
The quadrilateral is rotated 270° in a counterclockwise direction about the origin to produce quadrilateral A’B’C’D’. Which of the following is the graph of quadrilateral A’B’C’D’?
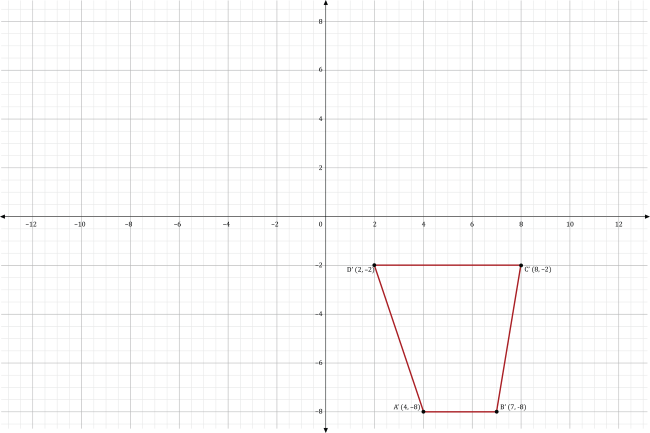
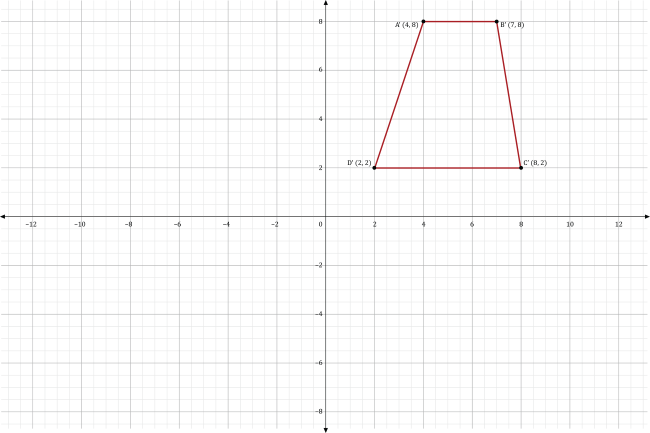
Rotating a point that has the coordinates \((x,y)\) 270° about the origin in a counterclockwise direction produces a point that has the coordinates \((y,-x)\). Substituting the coordinates for the vertices of quadrilateral ABCD into our formula to find the rotated vertices for quadrilateral A’B’C’D’, we get:
\(A’ (4,-8)\) \(B’ (7,-8)\) \(C’ (8,-2)\) \(D’ (2,-2)\)
The graph of the four rotated points is shown in the coordinate plane below.
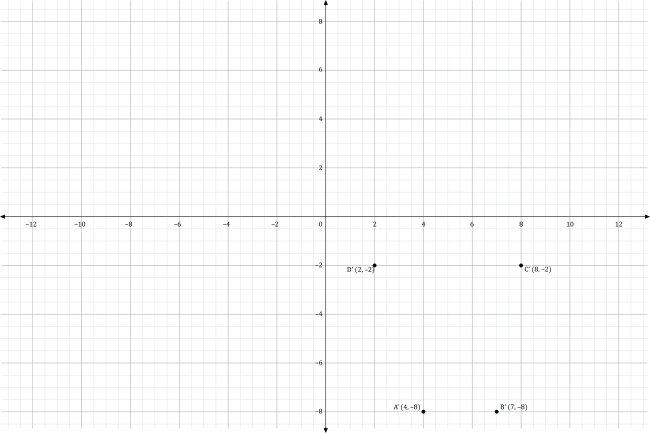
Connecting the vertices consecutively from A’ to D’ with four-line segments, we get the graph of quadrilateral A’B’C’D’ shown below.

A clock is superimposed on the coordinate plane so its center is at the origin of the coordinate plane, as shown below.
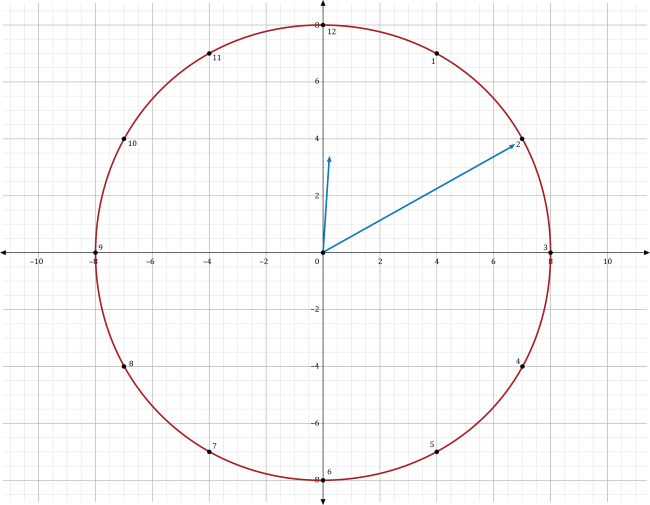
The clock reads 12:10 pm. If the minute hand is rotated 180° about the origin in a clockwise direction, what time will it be?
Rotating a point that has the coordinates \((x,y)\) 180° about the origin in a clockwise or counterclockwise direction, produces a point that has the coordinates \((-x,-y)\). While the end of the minute-hand of the clock does not lie at the point \((7,4)\), the time it represents in minutes does. Substituting the coordinates of this point into our formula to find the rotated point, we get \(\left(-7,-4\right)\).
Rotating the minute-hand of the clock in the direction of the rotated point, we can get a reading of what time it is.
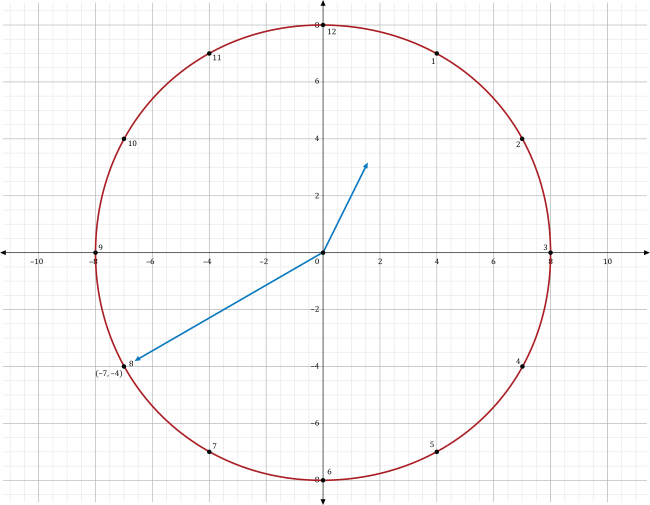
Each numerical value on the clock measures 5 minutes for the minute hand and 1 hour for the hour hand. Since the rotated point lies at the number 8 for the clock, the reading of the minute hand is 40 minutes. Since the rotation is clockwise the hour hand is also rotated clockwise to represent a time that is later than 12:10 pm., the correct time after the rotation of the minute-hand is 12:40 pm.
A water wheel has a diameter of 20 feet. Water from a water trough that is positioned above the water wheel is poured into the paddles of the water wheel to force it to rotate in a clockwise direction. The water in a paddle begins to be released from the water wheel after it makes a 90° rotation. If the water enters the paddle at the point shown on the graph in the coordinate plane below, what are the coordinates of the point where the water is released from the water wheel? The center of the water wheel is at the origin of the coordinate plane.
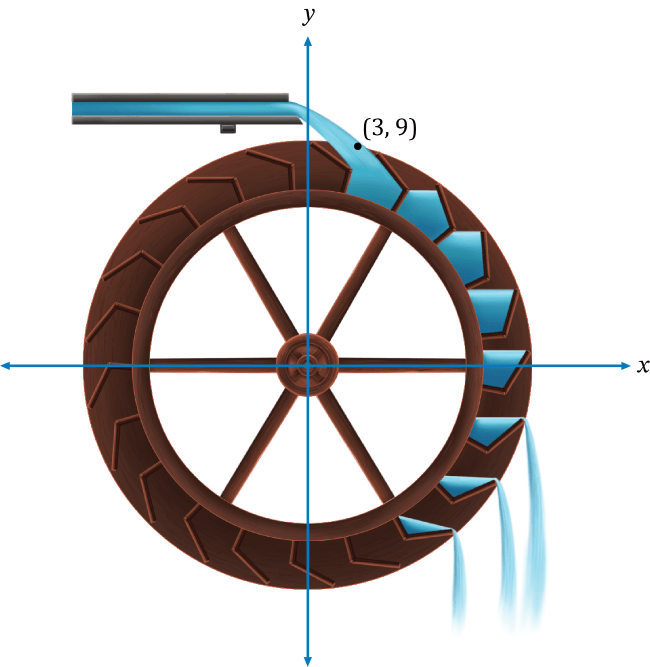
Rotating a point that has the coordinates \((x,y)\) 90° about the origin in a clockwise direction produces a point that has the coordinates \((y,-x)\). Substituting the coordinates for the point where the water enters a paddle into our formula, we get our rotated point of \((9,-3)\). Thus, the coordinates of the point where the water is released from the water wheel are \((9,-3)\).
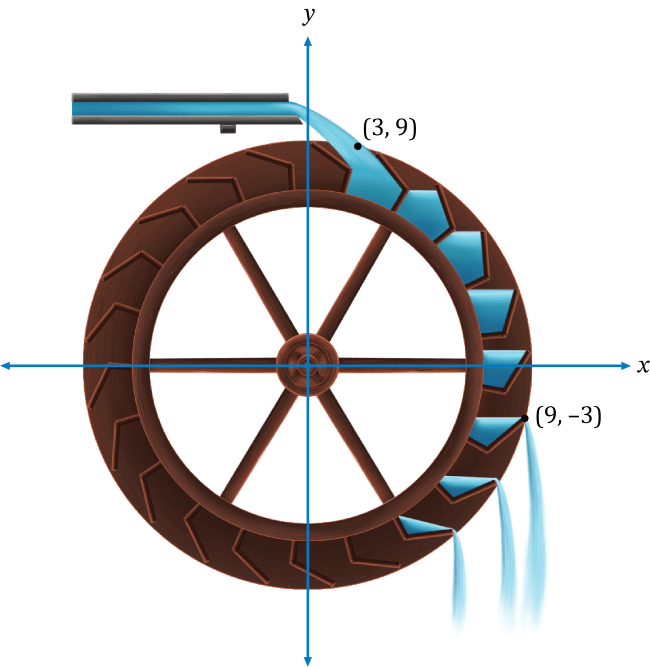
Notice at the rotated point in the coordinate plane, the water from a paddle is beginning to be released from the water wheel.





