
How Many Degrees are in a Triangle?
One of the first things we all learned about triangles is that the sum of the interior angles is 180 degrees.
You might have used this knowledge to find the missing angle in a triangle when you knew the other two, and all was well. But then a seed of doubt or curiosity may have crept in. How do we know that the sum of the angles is always 180? Is there some way that we can definitively prove it? The answer is yes!
To mathematically prove that the angles of a triangle will always add up to 180 degrees, we need to establish some basic facts about angles.
Angles of a Triangle
The first fact we need to review is the definition of a straight angle.
A straight angle is just a straight line, which is where it gets its name.
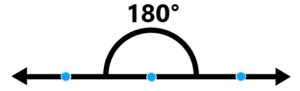
We’ve placed three points on it to represent the three angles of a triangle. The straight angle ABC is a 180-degree angle. This will be important later.
To see our next angles, let’s take two straight angles and have another line cross through them:
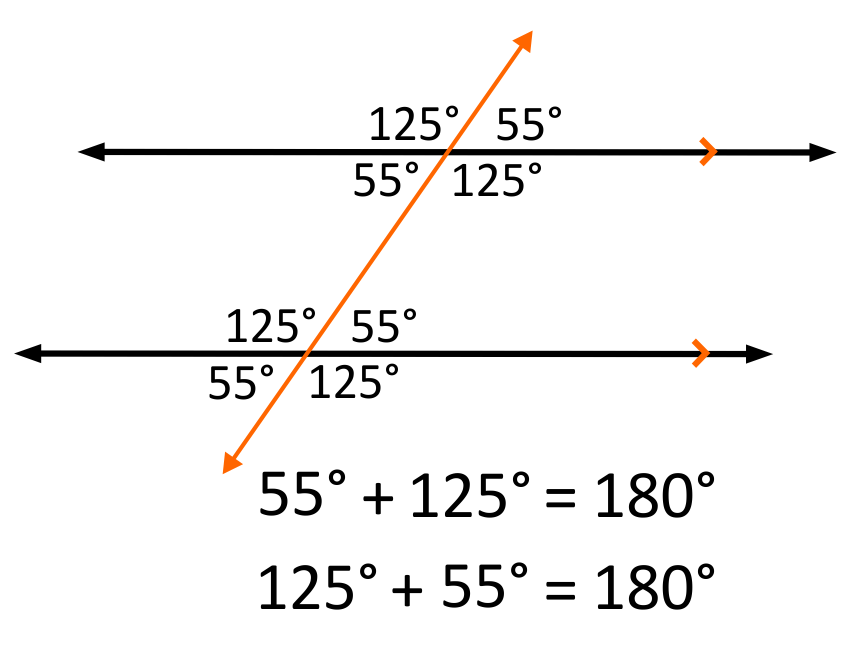
This is what we call a transversal. We can see that there are only two different angle measures when this happens. If we look between the parallel lines, we can see that the two angles on each side of the transversal line add up to 180 degrees.
This is because the transversal line cuts each of the parallel lines into two pieces. Since the straight line is a straight angle, when it’s cut in half its two halves must add up to the original measure. It’s just like if you cut a meter stick at any point, when you put the two pieces of the stick back together they will still add up to one meter.
If we draw one more line cutting across the parallel lines we can make a triangle.
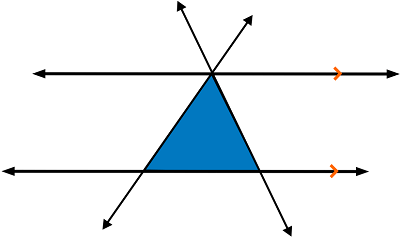
Our top group of angles has been changed from a group of four to a group of six because each of the bigger angles has been cut by the new line.
The group of angles on the bottom left is unchanged and there’s a new group of angles created by the new line crossing the bottom parallel line.
Let’s add some angle labels to all the angles between the parallel lines:
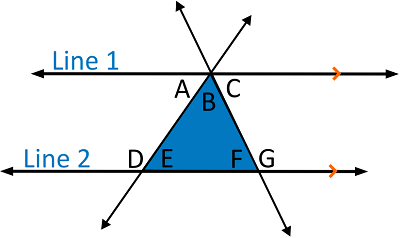
We can see that angles A, B, and C combine to form a straight angle, so that means that their sum must be 180 degrees. Now we can establish that the three angles inside the triangle (B, E & F) also add up to 180.
Angles A and E are congruent angles, which means they have the same measure, because they are alternate interior angles of a transversal with parallel lines.
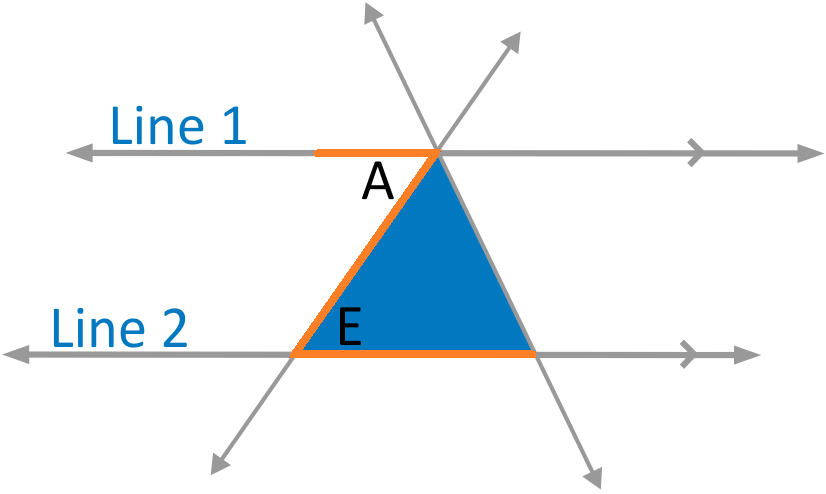
Angle C and Angle F are congruent for the same reason.
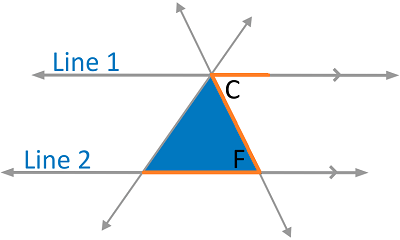
Angle B happens to be congruent with itself. Therefore, the sum of angles A, B, and C must be equal to the sum of the angles B, E, and F. And since the sum of angles A, B, and C is known to be 180, then the sum of angles B, E, and F must also be 180. Here’s a table that lays everything out for us:
| Statement | Reason |
|---|---|
| \(m \angle A+m \angle B+m \angle C=180 ^{\circ}\) | Definition of straight angle |
| \(m \angle A+m \angle E\) | Alternate interior angles of transversal congruent if parallel lines |
| \(m \angle C+m \angle F\) | Alternate interior angles of transversal congruent if parallel lines |
The definition of a straight angle is “The measure of angle A, plus the measure of angle B, plus the measure of angle C, equals 180 degrees.” “The measure of angle A equals the measure of angle E” is true because the two angles are congruent, alternate interior angles. The same applies to angles C and F.
Let’s look at it now with the angle measures in place:
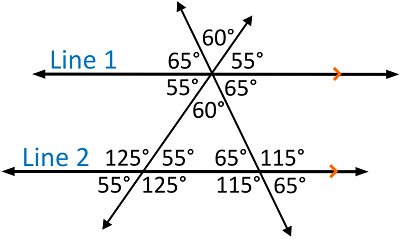
When we look at the three angles underneath Line 1, we can see that they add up to 180 degrees just as we know they must.
And the three angles in the triangle have the same three angle measures. This will always be true. If we rotate the line we added and look at the measures again we’ll see that it still works:
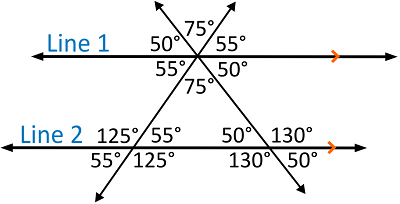
We have 55, 75, and 50 inside the triangle, and 55, 75, and 50 underneath line one. Add these together and you get, surprise, a 180-degree angle.
Review
Okay, before we go, let’s go over a couple of quick review questions!
1. What is the measure of a straight angle?
- 360°
- 180°
- 90°
- 0°
2. If two angles are alternate interior angles of a transversal with parallel lines, this means that the angles are also
- Congruent
- Acute
- Noncongruent
- Parallel
That’s all for this review! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you prove that a triangle is 180 degrees?
A
In a straight angle, such as \(∠A+∠B+∠C\) in the red circle, the three angles form \(180°\). The transversals created by the side lengths of the triangle form angle pairs that are congruent. For example, \(∠A\) and \(∠A\) are congruent because they are alternate interior angles. \(∠B\) and \(∠B\) are also congruent because they are also alternate interior angles. Since \(∠A=∠A\) and \(∠B=∠B\), we know that the interior angles \(∠A+∠B+∠C\) must also equal \(180°\).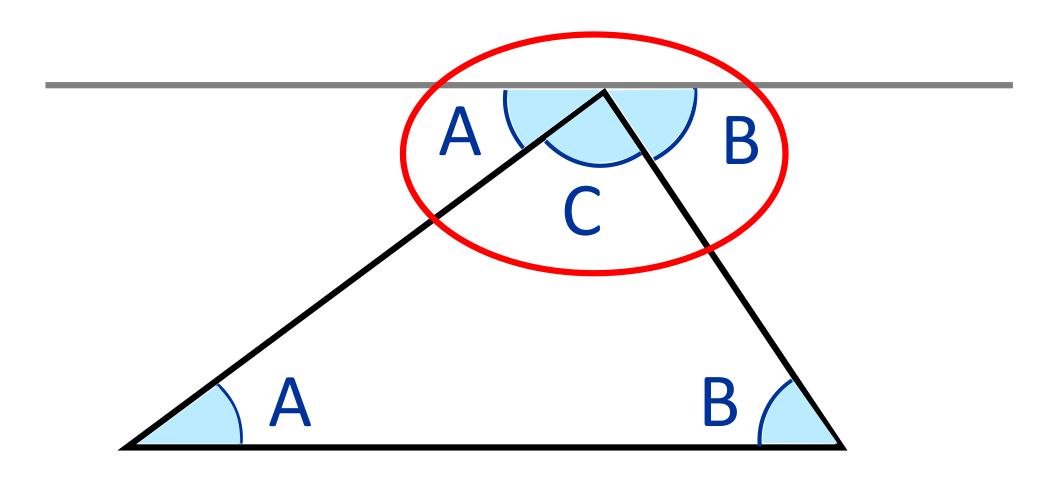
Q
Can a triangle be 180 degrees?
A
An angle that is \(180°\) is considered a straight angle, or essentially a straight line. The interior angles of a triangle need to have a sum of \(180°\), which means that none of the angles can individually be \(180°\).
Q
Why can’t a triangle have an 180-degree angle?
A
The three interior angles of a triangle will always have a sum of \(180°\). A triangle cannot have an individual angle measure of \(180°\), because then the other two angles would not exist \((180°+0°+0°)\). The three angles of a triangle need to combine to \(180°\).
Q
What is the angle sum of a triangle?
A
The angle sum of a triangle will always be equal to \(180°\). The angle sum of a quadrilateral is equal to \(360°\), and a triangle can be created by slicing a quadrilateral in half from corner to corner. Since a triangle is essentially half of a quadrilateral, its angle measures should be half as well. Half of \(360°\) is \(180°\).
For example, the sum of the angles of the quadrilateral below is \(360°\) because it consists of four \(90°\) angles. The pink triangle is half of this, therefore the sum of its angle measures should also be half \((180°)\).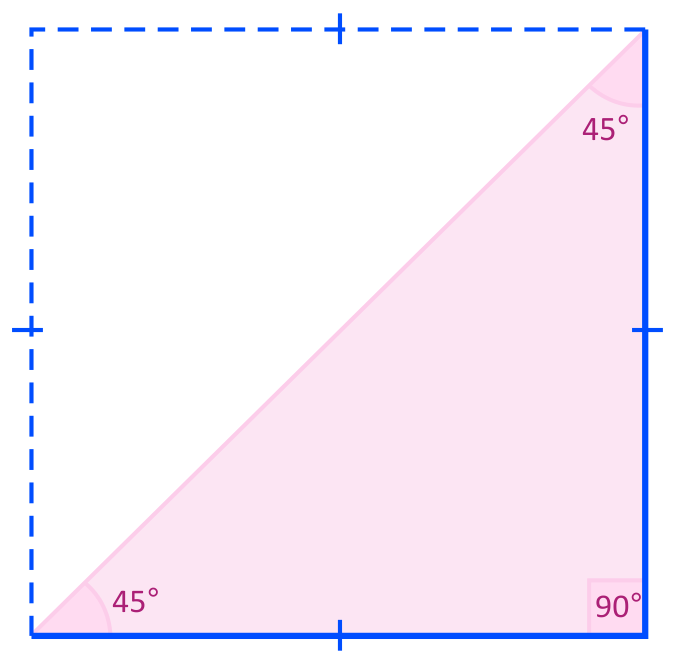
Q
What angle equals 180 degrees?
A
An angle of \(180°\) will always form a straight line. This line is also referred to as a straight angle. One way to prove that a straight angle is \(180°\) is to put two right angles together. Two \(90°\) angles will form a \(180°\) angle, or straight line.