Finding the Volume and Surface Area of a Right Circular Cylinder
Hello, and welcome to this video about cylinders! In this video, we will explore how to find the volume and surface area of any cylinder. Let’s learn about cylinders!
Cylinders are one of the most common three-dimensional shapes that we see around us. Most food and drink cans are shaped like a cylinder. Another quite common item that we see daily that is shaped like a cylinder is a battery. Take a look around you, can you see any cylindrical shapes?
As you can see, all these objects have a circular top and bottom and a curved surface. A cylinder is a three-dimensional figure with two circular bases that are parallel to each other and are joined by a curved surface. The perpendicular distance that connects the bases of the cylinder is the height and the axis is the line that extends through the centers of the circular bases.
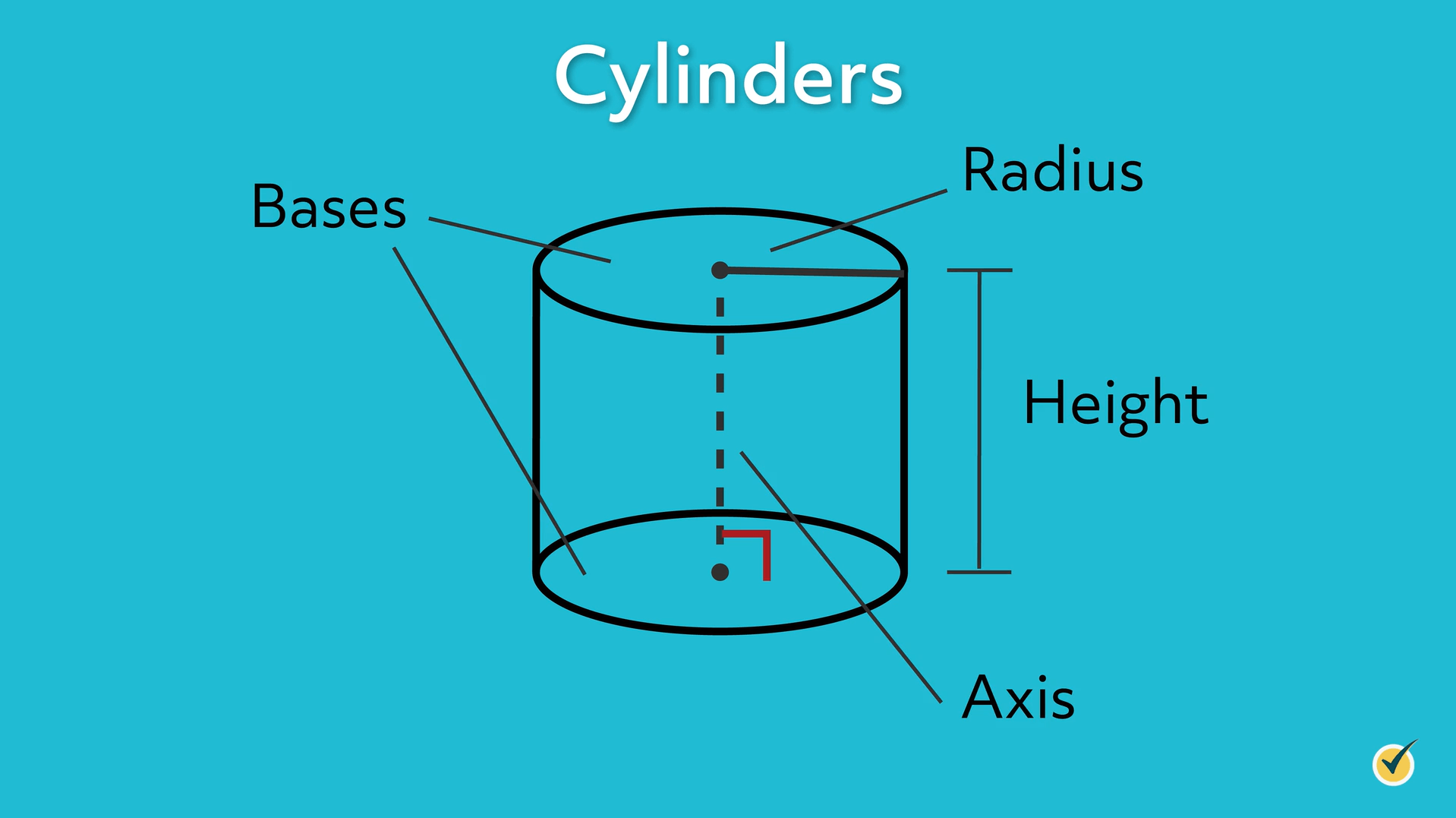
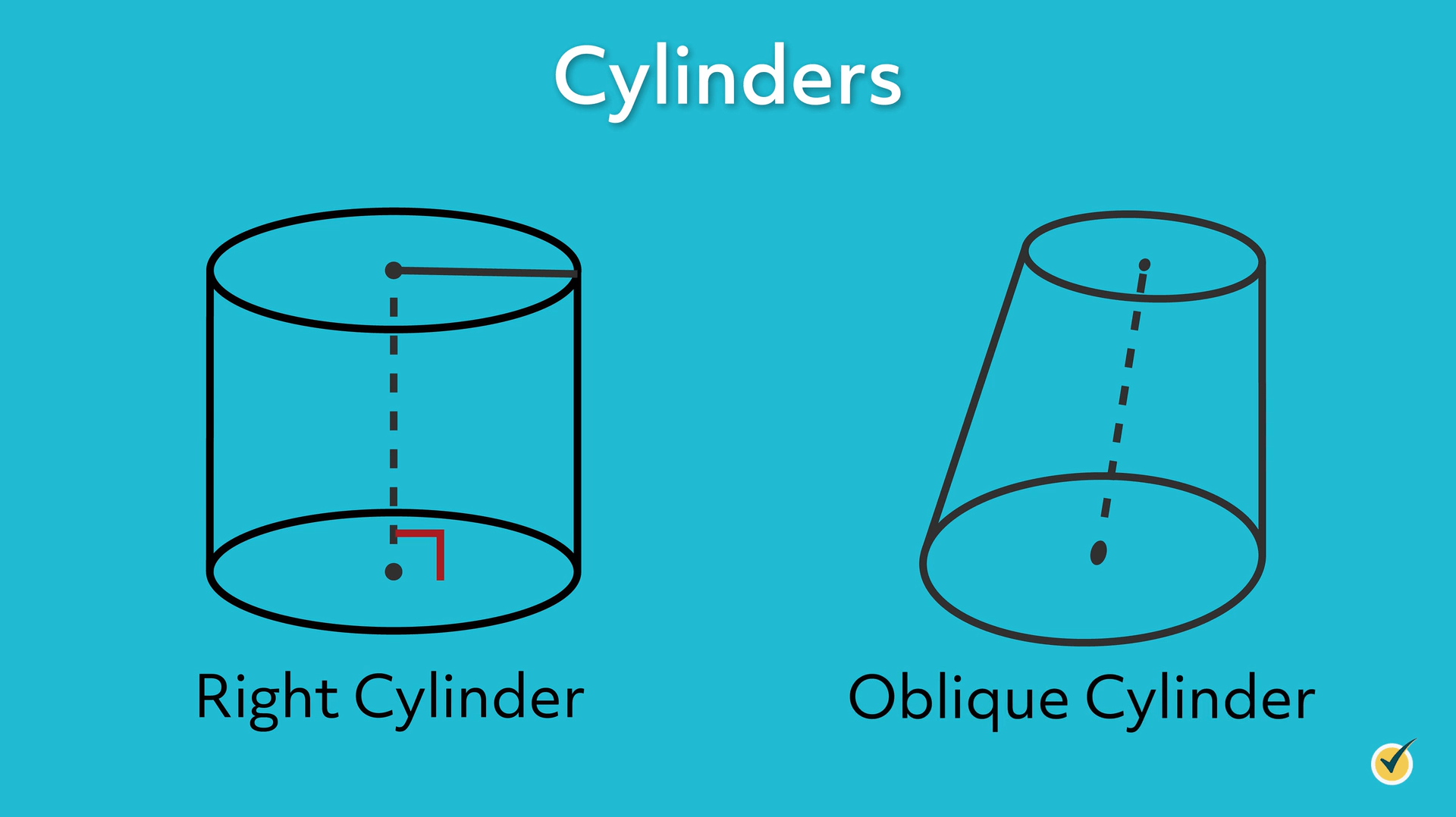
A cylinder where the axis is perpendicular to the bases is called a right cylinder. A cylinder where the axis is not perpendicular to the bases is called an oblique cylinder.
Let us recall what volume and surface area of three-dimensional figures are and how we go about finding them.
The volume of a three-dimensional figure is the amount of liquid it can hold, and it is measured in cubic units.
The surface area of a three-dimensional figure is the total area that the surface of the figure covers and is measured in square units.
The formula for the volume (V) and surface area (SA) of a cylinder are shown. To calculate the volume and surface area of any cylinder, we need the radius and the height of the cylinder. The formula for the area of a circle is \(A=\pi r^{2}\)
It is no surprise that the formula appears in both the volume and surface area formulas for a cylinder since the bases of a cylinder are circles.
Volume of a Cylinder Formula
Very much like other three-dimensional figures, the volume of a cylinder is the area of its circular base multiplied by the height.
\(V=\pi r^{2}h\)
\(SA=2\pi rh+2\pi r^{2}\)
\(h\) = height of cylinder
How to find the Surface Area of a Cylinder
The surface area, as we mentioned before, is the total area that covers the surface of the figure. This might be easier to see if we open the cylinder up and look at its net. The area of the two circular bases is the \(2\pi r^{2}\) part of the surface area formula. Once the cylinder is open, we can see the curved part of the cylinder is really a rectangle and the side lengths of the rectangle are determined by the circumference of the circular base \(2\pi r\) and the height of the cylinder \(h\).
Let’s look at an example:
What is the volume and surface area of a cylinder where the diameter of the base is 18mm and the height of the cylinder is 20mm? (Leave your answer in terms of \(\pi \))
So, to find the volume and surface area, we need the radius and the height of the cylinder. Since the radius is half of the diameter, we can just divide 18 by 2, so the radius of the circular base is just 9 millimeters. Now we can substitute the values into the formula and evaluate.
\(V=\pi r^{2}h=\pi (9\text{ mm})^{2}(20\text{ mm})=1,620\pi \text{ mm}^{3}\)
\(SA=2\pi rh+2\pi r^{2}=2\pi (9)(20)+2\pi (9)^{2}=360\pi +162\pi =522\pi \text{ mm}^{2}\)
Let’s look at another example.
The surface area of a cylinder is 502.4 ft² and the radius of the base is 5 ft. What is the height of the cylinder? (Use 3.14 for \(\pi\))
We will start by substituting the values we know into the surface area formula.
As you can see there is only one unknown, \(h\), so we will use our algebra skills to solve for the unknown.
simplify each term
\(502.4=2(3.14)(5)h+2(3.14)(5)^{2}\)
isolate the term with the variable
\(502.4=31.4h+157\)
combine like terms
\(502.4-157=31.4h+157-157\)
solve for h
\(345.4=31.4h\)
divide both sides by the coefficient to isolate the variable
\(\frac{345.4}{31.4}=\frac{31.4}{31.4}h\)
Therefore, the height of the cylinder is 11 ft.
\(11=h\)
Joan has a water tank at her shop that is 34.8 inches high and the diameter of the circular base is 20.6 inches. She wants to get a label made for the side of the tank with her business logo and needs to calculate the lateral area, which is the surface area without the area of the bases. What is the area of the label? (Use 3.14 for \(\pi\))
Since we only need the lateral area, we can remove the area of the circles from our formula.
\(\text{lateral area }(LA)=2\pi rh\)
Remember, the formula asks for the radius of the base, so we will divide 20.6 by 2 to get 10.3, which is the length of the radius.
\(LA=2\pi rh=2(3.14)(10.3)(34.8)=2,251 \text{ in}^{2}\)
So the area of our label will need to be \(2,251\text{ in}^{2}\).
I hope that this video on volume and surface area of a cylinder was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you calculate the surface area of a cylinder?
A
Calculate the surface area of a cylinder by using the formula \(SA=2πr^2+2πrh\), where r is the radius of the circular base and h is the height of the cylinder.
Ex. Find the surface area of this cylinder.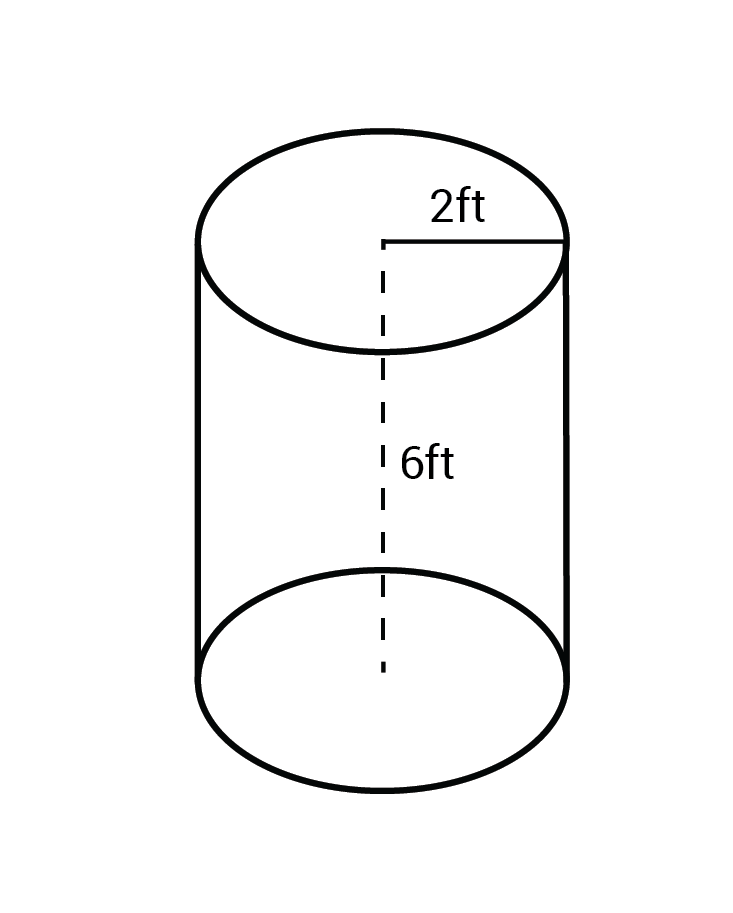
Find the surface area by using the formula \(SA=2πr^2+2πrh\). The radius (r) measures 2 ft and the height (h) measures 6 ft.
\(SA=2π(2\text{ ft})^2+2π(2\text{ ft})(6\text{ ft})\)
\(=8π\text{ ft}^2+24π\text{ ft}^2\)
\(=32π\text{ ft}^2\)
\(≈100.53\text{ ft}^2\)
Q
What is the surface area formula?
A
The general formula for surface area of a prism is \(SA=2B+ph\), where B is the area of the base, p is the perimeter of the base, and h is the height of the prism.
Remember, a cylinder is a special kind of prism with circular bases, so you can substitute \(πr^2\) for B (area of the base) and \(2πr\) for p (perimeter of the base). The formula for surface area of a cylinder is \(SA=2πr^2+2πrh\).
Q
What is the shape of the base of a cylinder?
A
The shape of the base of a cylinder is a circle.
Q
How do you find the volume of a cylinder?
A
The equation that we use in order to find a cylinder’s volume is: \(V=πr^2h\), where the \(r\) stands for the cylinder’s radius and the \(h\) represents the cylinder’s height. We simply plug these values into the volume equation, and we get our desired output!
Ex. Find the volume of a cylinder whose radius is \(5\) inches and has a height of \(2\) inches.
\(V=π×5^2×2\)
\(V=π×25×2\)
\(V=50π\)
\(V≈157.1\text{ in}^3\)
Q
What is the radius of a cylinder?
A
We know that the radius of a circle is half of its diameter, and we know that cylinders have \(2\) (same-sized) circular bases at each end. Hence, the radius of a cylinder is the radius of its circular bases.
What is the radius of this cylinder?
\(r=8\text{ cm}\)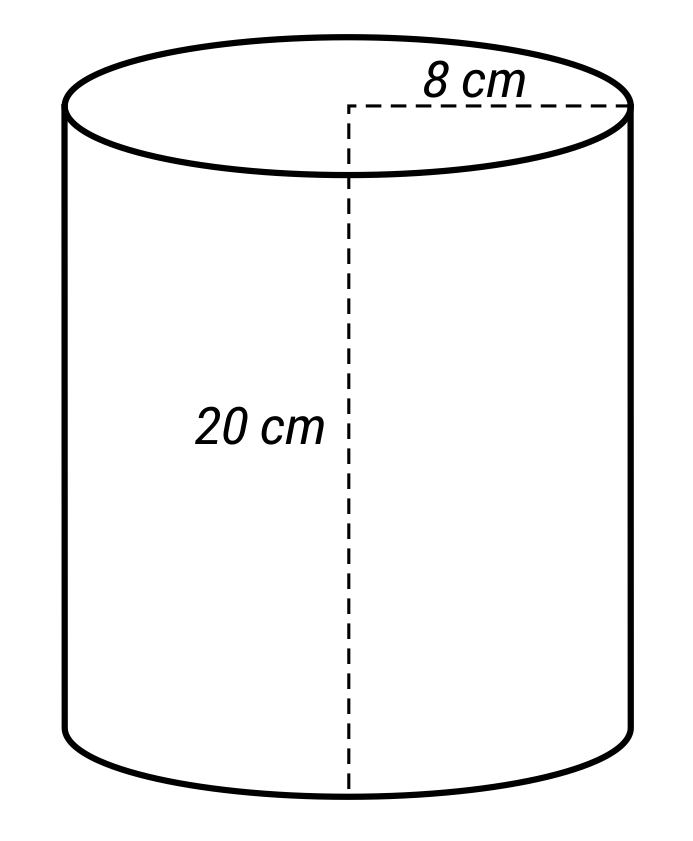
Q
How do you find the radius of a cylinder with just the volume?
A
This is actually a trick question! We know that the volume equation has three “unknowns,” namely: \(V\), \(r\), and \(h\). Right now, we can’t solve an equation like \(V=πr^2h\) without knowing at least two of the three variables. (Note: we can use any combination of two variables in order to find the remaining one. For example, if we wanted to find an unknown radius, we would need to know the volume and the height of that cylinder first; for an unknown height, we’d need the radius and volume; and, of course, for an unknown volume, we’d need the radius and height.)
*In order to find the radius of a cylinder when we’ve been given both the height and the volume, we would simply need to rearrange the volume equation to get the r alone on one side of the ‘equals’ sign. Take a look:
\(V=πr^2h\)
\(\frac{V}{hπ}=r^2\)
\(\sqrt{\frac{V}{hπ}}=r\)
Q
How do you find the height of a cylinder given the volume?
A
Since we can’t solve an equation like \(V=πr^2h\) without knowing at least two of the three variables, this wouldn’t be possible without also knowing the cylinder’s radius. If we have both the radius and the volume, though, we can rewrite the volume equation as: \(\frac{V}{πr^2}=h\).
Ex. Find the height of a cylinder whose volume is \(36π\text{ inches}\) and whose radius is \(3\text{ inches}\).
\(h=\frac{36π}{π×3^2}\)
\(h=\frac{36π}{9π}\)
\(h=4\text{ inches}\)
Q
What is the difference between curved surface area and total surface area?
A
Curved surface area is the area of the middle portion of the cylinder. Total surface area includes the curved surface area and the area of the two circular bases. The equation for total surface area of a cylinder is found by combining the area of Base 1, the curved surface area, and the area of Base 2. Consider…
\(\text{Area of Base }1=πr^2\)
\(\text{Curved Surface Area }=2πrh\)
\(\text{Area of Base 2 }=πr^2\)
\)
Ex. Find (a) the curved surface area and (b) the total surface area of a cylinder with a radius of \(10\) units and a height of \(15\) units.
- \(\text{Curved Surface Area }=2π\times10\times15\)
\(\text{Curved Surface Area }=300π\)
\(\text{Curved Surface Area }\approx 942.5\text{ units}^2\) - \(SA=2π\times10\times(10+15)\)
\(SA=2π\times10\times25\)
\(SA=500π\)
\(SA\approx 1{,}570.8\text{ units}^2\)
Q
What is the formula for curved surface area of a cylinder?
A
The formula for the curved surface area of a cylinder is \(2πrh\). Think of the curved portion of a cylinder as a rectangular sheet that you wrap around the 3D object. It’s essentially a rectangle whose length is the circumference of the circular base that it lines (this is where the \(2πr\) comes from) and whose width is the height of the cylinder (this is where the \(h\) comes from).
Q
What is another name for curved surface area?
A
“Curved surface area” is sometimes referred to as, “lateral area.” Hence, we could write the respective equation as \(L=2πrh\). In the case of an open cylinder (meaning: a cylinder without the two circular bases [Think of an empty paper towel roll!]), the total surface area would actually just be the lateral area.
Volume and Surface Area of a Right Circular Cylinder Practice Questions
Calculate the surface area of the following cylinder.
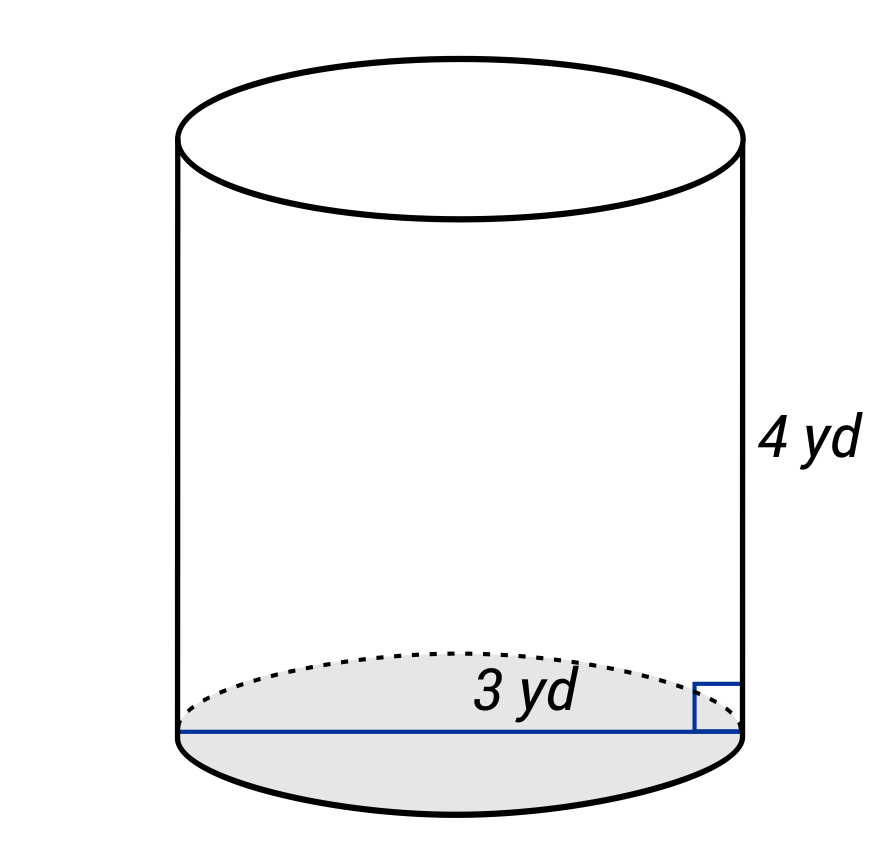
The volume of a cylinder can be calculated using the formula \(SA=2πr^2+2πrh\). A cylinder consists of two circles and one rectangle. The surface area of a circle is found using the formula \(πr^2\),so \(2πr^2\) will allow us to find the surface area of the top and bottom faces of the cylinder. The rectangle that wraps around the cylinder has a height that is 10 cm, and a width that is \(2πr\). Essentially, the width of the rectangle is the circumference of the circle.
When the height (h), radius (r), and an approximation of \(π\) (3.14) are plugged into the formula \(SA=2πr^2+2πrh\), it becomes \(SA=2(3.14)(1.5)^2+2(3.14)(1.5)(4)\). This simplifies to \(SA=14.13+37.68\), which reduces to 51.81. The surface area of the cylinder is 51.81 yd2.
Calculate the volume of the following cylinder.
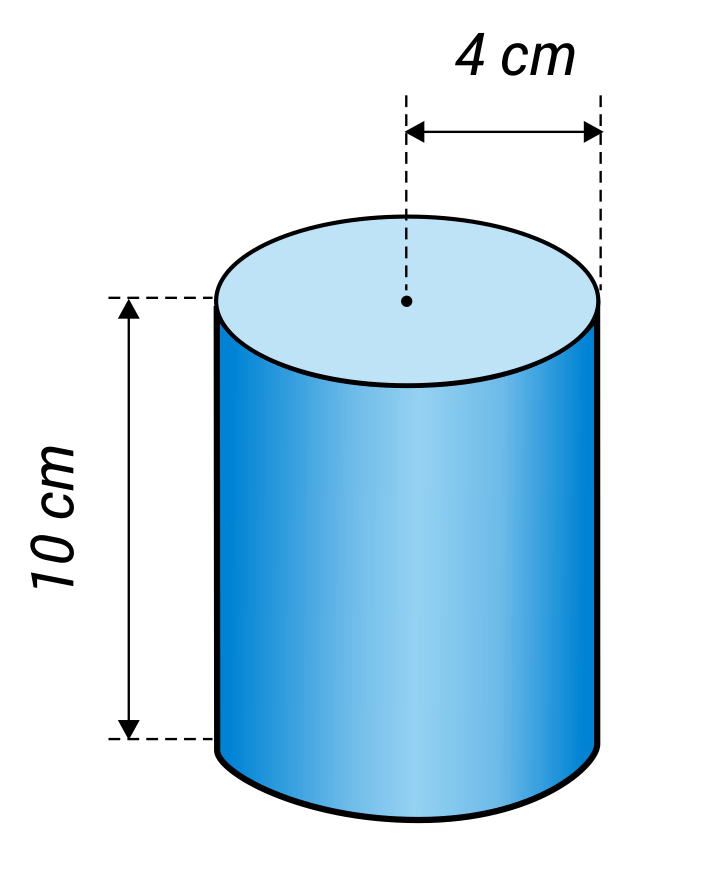
The volume of a cylinder can be calculated using the formula \(V=πr^2(h)\). When determining the volume of a cylinder, you are simply finding the area of the circular base shape and then multiplying this by the height. The radius of the circular base shape in this cylinder is 4 cm, and the height is 10 cm. These two values can be plugged into the formula so that \(V=πr^2(h)\) becomes \(V=π(4)^2(10)\). When the approximation of pi (3.14) is substituted in for the symbol \(π\), the equation simplifies to 502.4. The volume of the cylinder is 502.4 cm3.
A grain silo consists of a cylinder with a dome on top. Farmer Jenkis needs to calculate the volume of grain contained in a silo that has a cylinder height of 50 feet and a cylinder diameter of 10 feet. The dome will remain empty. If the cylindrical portion of the grain silo is completely full, what is the total volume of grain?
Since the dome shape will remain empty, the volume of the grain silo can be calculated using the formula \(V=πr^2h\). The radius of the silo is 5 feet and the height is 50 feet. When these two values are plugged into the formula, along with an approximation for pi (3.14), \(V=πr^2h\) becomes \(V=(3.14)(5)^2(50)\). This simplifies to 3,925. The silo contains 3,925 ft3 of grain.
Max makes candles to sell at his local farmers market. The candles that he makes are cylindrical. He bought a new candle mold, and he needs to figure out how much melted wax it can hold. The cylindrical mold has a height of 10 inches, and a radius of 5 inches. How much melted wax can he pour into the mold if he wants to fill it completely?
To calculate the volume of wax that can be poured into the cylindrical mold, we can use the formula \(V=πr^2(h)\). We know that the height of the cylinder is 10 inches, and the radius is 5 inches. When we plug these into the formula, along with an approximation of π (3.14), \(V=πr^2(h)\) becomes \(V=(3.14)(5)^2(10)\), which simplifies to 785. The candle mold can hold 785 in3 of melted wax.
Julia wants to upcycle three old fruit cans. Each can is 5 inches tall and has a radius of 2 inches. She plans on painting the cans and using them as flower pots. If she only wants to paint the sides of the cylinders and the bottoms, what is the total surface area she will need to paint?
In order to calculate the surface area of the three cans, we can make a few slight adjustments to the formula \(SA=2πr^2+2πrh\). Since Julia is only painting the sides of the cans \((2πrh)\), and the bottoms of the cans \((πr^2)\), we can adjust the formula so that we are adding three circles and three rectangles. The formula \(SA=2πr^2+2πrh\) becomes \(SA=3πr^2+3(2πrh)\). When we plug in 2 for the radius, 5 for the height, and 3.14 as an approximation for π, the formula becomes \(SA=3(3.14)(2)^2+3(2(3.14)(2)(5))\), which simplifies to 226.08. Julia will need to paint a total of 226.08 in2.