
What is an ellipse?
You might describe it as a squashed circle, which would be correct. But, in mathematics, an ellipse has a much more specific definition, which is “a closed curve where the sum of the distances from the two focus points inside the curve to every point on the curve is constant.” An ellipse is not to be confused with an oval, which does not have a lovely mathematical definition like the ellipse does.
Foci of an Ellipse
Let’s take a look at an ellipse so we can see those two focus points, which together we call foci:
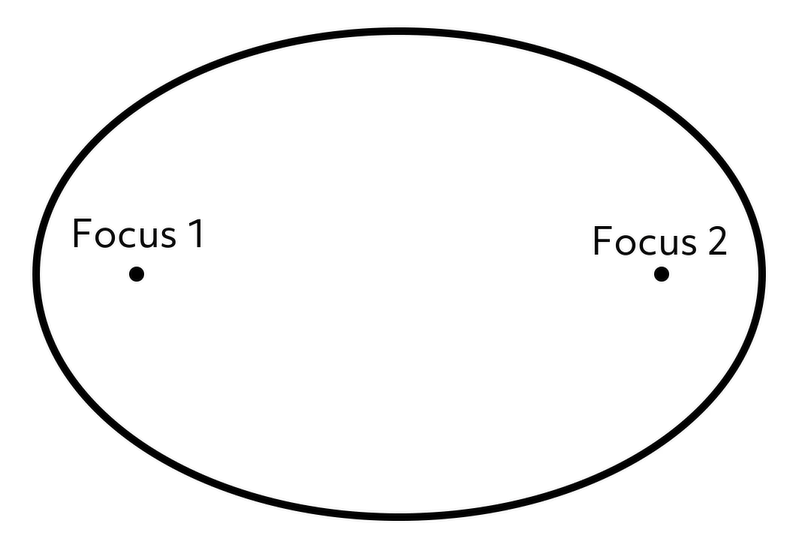
We can illustrate the mathematical definition of an ellipse by showing a point on the ellipse along with connecting lines to the foci:
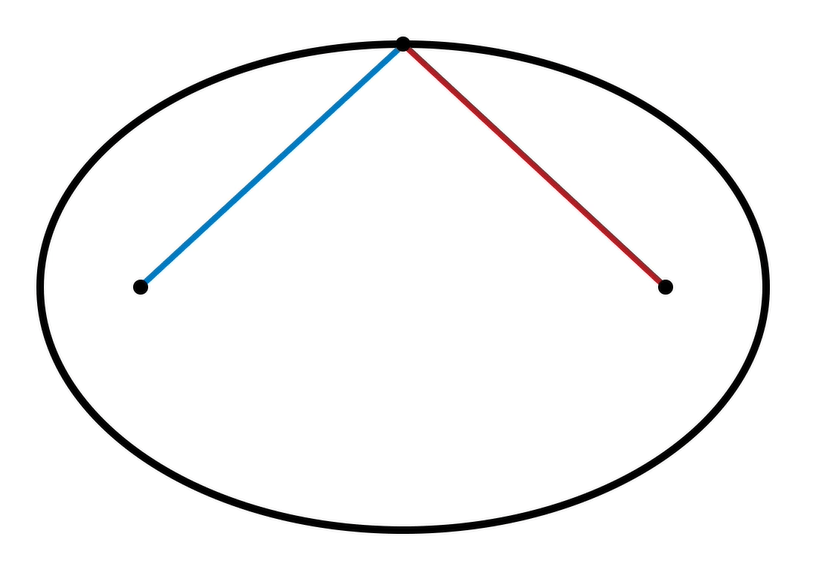
If we measure these two line segments and then add them together, that will be the total length from any point on this ellipse to the two focus points. Depending on where the point is on the ellipse, the blue line will sometimes be shorter and the red line longer, but they’ll always add to the same amount.
Now let’s talk more about those focus points. We find them on the major axis of the ellipse, which is always the longer of the two axes:
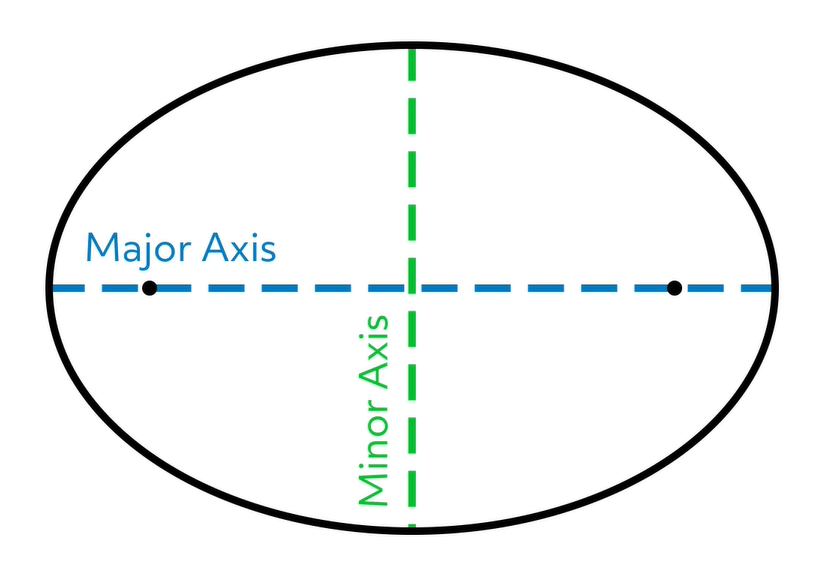
Depending on the ellipse, the foci get closer to or farther from the center! Look at this ellipse that’s not quite as squashed:
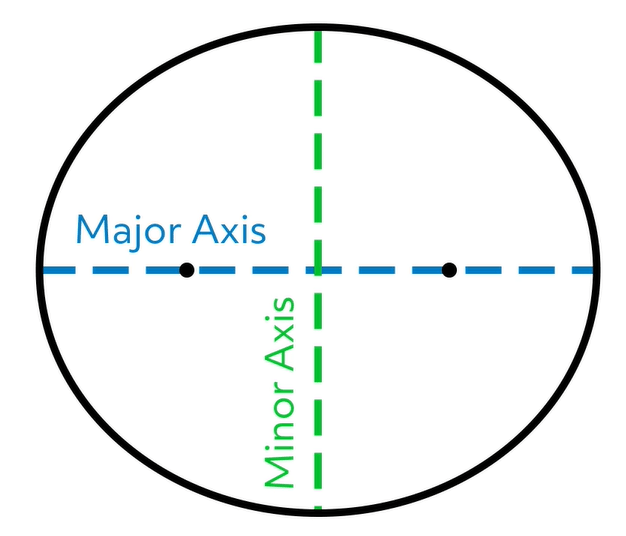
Eccentricity
Notice how the focus points are closer to the center of the ellipse in this one. This is due to something we call eccentricity, which is expressed as a value between 0 and 1. We can calculate the eccentricity by creating a ratio. We measure the distance from either focus point to the center and place that over the distance from that focus point to either end of the minor axis.
When the eccentricity is 0, we have a very special kind of ellipse that we call a circle. When that happens, it means that the two focus points have converged into one point at the center of the ellipse.
At the opposite end of the spectrum is a totally flattened ellipse and those two measures will be the same, resulting in an eccentricity of 1. It also means our “ellipse” will look like a line segment; it’s totally flattened with the foci as the endpoints of the line segment.
Here is the standard form of an equation of an ellipse:
We have a lot of letters to define here. The center of the ellipse is represented by \(h\) and \(k\), which form an ordered pair. The coefficient \(a\) is the length from the center of the ellipse to either end of the ellipse parallel to the \(x\)-axis, and \(b\) is the length from the center to either end of the ellipse parallel to the \(y\)-axis.
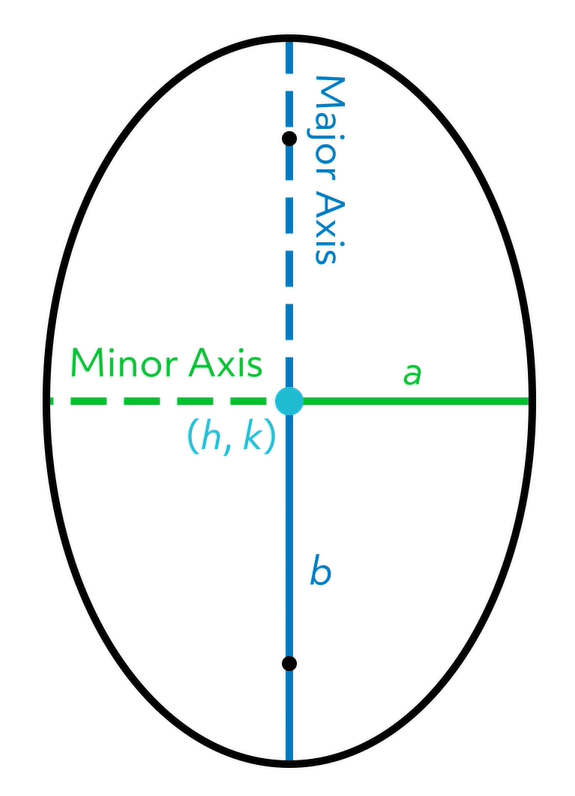
We can see that, in this case, \(b\) is equal to half the length of the major axis, which in this case is the height of the ellipse, and \(a\) is half the minor axis, which is the width. So if we want to create an ellipse with a height of 14 units and a width of 10 units, \(b\) would be equal to half of 14 which is 7, and \(a\) would be equal to half of 10 which is 5.
If we wanted that ellipse to be located with a center at \((-3,2)\), our equation would look like this:
We substituted the \(x-\) and \(y-\) values of our center \((-3,2)\) for \((h,k)\). Notice that since \(h\) is negative, it changes the sign inside the left binomial to a plus sign. This is because subtracting -3 is the same thing as adding 3. Our denominators are just the squared versions of our \(a\) and \(b\). \(a\) is 5, which squares to 25, and \(b\) is 7, which squares to 49.
Practice Problems
Okay, to wrap things up, let’s go through a couple of practice problems. Feel free to pause the video after each question to work it out on your own.
1. What is the equation of an ellipse that has a center at \((6,4)\), has a height of 12, and a width of 8?
We start with the standard form of an equation for an ellipse.
Next, we substitute the \(x-\) and \(y-\)values of the center for \(h\) and \(k\) in our general equation.
Finally, we take half of the width, which is the minor axis, to find our value for \(a\) (half of 8 is 4). We then square it after substituting it into the general equation for our first denominator of 16. We do the same thing for \(b\). Take half of the height (half of 12 is 6) and substitute it in for \(b\), where it is squared to become 36. Done!
2. What is the equation of this ellipse:
This one is a little tougher because we need to find the length of both axes, as well as find the center of the ellipse. We start with the standard form for an equation of an ellipse:
Next, we need to determine how tall and wide our ellipse is. By looking at the diagram, we can see that it is 8 units tall and 6 units wide. We also need to find the center, which we can do by drawing the major and minor axes. Here, we find the center at \((-1,1)\). Now we can substitute the \(x-\) and \(y-\)values of the center for \(h\) and \(k\) in our general equation.
When we substitute the \(h\), we end up with \((x – (-1))^{2}\) , which can be rewritten as \((x+1)^{2}\) because subtracting a negative is the same thing as adding. Finally, we take half of the width, which is the minor axis, to find our value of \(a\) (half of 6 is 3). We then square it after substituting it into the standard form equation for our first denominator of 9. We do the same thing for \(b\). Take half of the height (half of 8, which equals 4) and substitute it in for \(b\), where it is squared to become 16.
That’s all for this review of ellipses. Thanks for watching, and happy studying!
Ellipse Practice Questions
What is the equation of an ellipse that has a center at \((3,1)\), has a height of 8 units, and has a width of 4 units?
Start with the equation of an ellipse in standard form.
\(\frac{{(x-h)}^2\ }{a^2}+\frac{{(y-k)}^2}{b^2}=1\)
Next, substitute the \(x\)– and \(y\)-values of the center point for \(h\) and \(k\) in our general equation:
\(\frac{{(x-3)}^2\ }{a^2}+\frac{{(y-1)}^2}{b^2}=1\)
The value of \(a\) is half the width. Since half of 4 is 2, substitute 2 for \(a\). Square this value after substituting it into the general equation to get a denominator of 4 in the first fraction.
\(\frac{{(x-3)}^2\ }{4}+\frac{{(y-1)}^2}{b^2}=1\)
The value of \(b\) is half the height. Since half of 8 is 4, substitute 4 for \(b\). Square this value after substituting it into the general equation to get a denominator of 16 in the second fraction. Therefore, the equation of this ellipse is:
\(\frac{{(x-3)}^2\ }{4}+\frac{{(y-1)}^2}{16}=1\)
What is the equation of this ellipse?
Start with the equation of an ellipse in standard form.
\(\frac{{(x-h)}^2\ }{a^2}+\frac{{(y-k)}^2}{b^2}=1\)
We need to find the center, which is plotted on the coordinate plane. This center point is located at the origin, \((0,0)\). Substitute the \(x\)– and \(y\)-values of the center point for \(h\) and \(k\) in our general equation. Since \(h=0\), write the first numerator as \(x^2\). Since \(k=0\) as well, write the second numerator as \(y^2\).
\(\frac{x^2\ }{a^2}+\frac{y^2}{b^2}=1\)
Next, determine how tall and wide the ellipse is. By looking at the graph, we can see that it is 20 units tall and 8 units wide. Take half of the width to find the value for \(a\). Since half of 8 is 4, substitute 4 for \(a\). Square this value after substituting it into the general equation to get a denominator of 16 in the first fraction.
\(\frac{x^2\ }{16}+\frac{y^2}{b^2}=1\)
Take half of the height to find the value for \(b\). Since half of 20 is 10, substitute 10 for \(b\). Square this value after substituting it into the general equation to get a denominator of 100 in the second fraction. Therefore, the equation of this ellipse is:
\(\frac{x^2\ }{16}+\frac{y^2}{100}=1\)
What is the equation of an ellipse that has a center at (1,-5), has a height of 6 units, and has a width of 18 units?
Start with the equation of an ellipse in standard form.
\(\frac{{(x-h)}^2\ }{a^2}+\frac{{(y-k)}^2}{b^2}=1\)
Next, substitute the \(x\)– and \(y\)-values of the center point for \(h\) and \(k\) in our general equation. Since subtracting –5 is the same thing as adding 5, write the second numerator as \({(y+5)}^2\).
\(\frac{{(x-1)}^2\ }{a^2}+\frac{{(y+5)}^2}{b^2}=1\)
Then, take half of the width to find the value for \(a\). Since half of 18 is 9, substitute 9 for \(a\). Square this value after substituting it into the general equation to get a denominator of 81 in the first fraction.
\(\frac{{(x-1)}^2\ }{81}+\frac{{(y+5)}^2}{b^2}=1\)
Take half the height to find the value for \(b\). Since half of 6 is 3, substitute 3 for \(b\). Square this value after substituting it into the general equation to get a denominator of 9 in the second fraction. Therefore, the equation of this ellipse is:
\(\frac{{(x-1)}^2\ }{81}+\frac{{(y+5)}^2}{9}=1\)
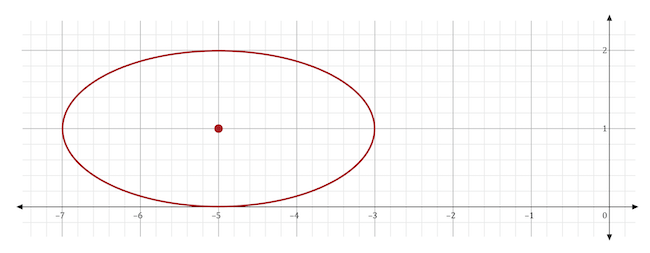
Ralph is installing a window above his front door. A scaled version of the window is graphed on the coordinate plane as the ellipse shown below. What is the equation of this ellipse?
Start with the equation of an ellipse in standard form.
\(\frac{{(x-h)}^2\ }{a^2}+\frac{{(y-k)}^2}{b^2}=1\)
We need to find the center, which is plotted on the coordinate plane. The coordinates of this center point are \((-5,1)\). Substitute the \(x\)– and \(y\)-values of the center point for \(h\) and \(k\) in our general equation. Since subtracting –5 is the same thing as adding 5, write the first numerator as \({(x+5)}^2\). Write the second numerator as \(\left(y-1\right)^2\).
\(\frac{{(x+5)}^2\ }{a^2}+\frac{{(y-1)}^2}{b^2}=1\)
Next, determine the height and width of the ellipse. By looking at the graph, we can see that it is 2 units tall and 4 units wide. Take half of the width to find the value of \(a\). Since half of 4 is 2, substitute 2 for \(a\). Square this value after substituting it into the general equation to get a denominator of 4 in the first fraction.
\(\frac{{(x+5)}^2\ }{4}+\frac{{(y-1)}^2}{b^2}=1\)
Take half the height to find the value for \(b\). Since half of 2 is 1, substitute 1 for \(b\). Square this value after substituting it into the general equation to get a denominator of 1 in the second fraction. Therefore, the equation of the ellipse for Ralph’s window is:
\(\frac{{(x+5)}^2\ }{4}+\frac{{(y-1)}^2}{1}=1\)
Charlotte is installing a swimming pool in her backyard. A scaled version of the pool can be graphed on the coordinate plane as an ellipse. The graph of Charlotte’s swimming pool has its center at \((0,3)\), a width of 14 units, and a height of 10 units. What is the equation of this ellipse?
Start with the equation of an ellipse in standard form.
\(\frac{{(x-h)}^2\ }{a^2}+\frac{{(y-k)}^2}{b^2}=1\)
The coordinates of the center point are \((0,3)\). Substitute the \(x\)– and \(y\)-values of the center point for \(h\) and \(k\) in our general equation. Since \(h=0\), write the first numerator as \(x^2\). Since \(k=3\), write the second numerator as \(\left(y-3\right)^2\).
\(\frac{x^2\ }{a^2}+\frac{{(y-3)}^2}{b^2}=1\)
Take half of the width to find the value for \(a\). Since half of 14 is 7, substitute 7 for \(a\). Square this value after substituting it into the general equation to get a denominator of 49 in the first fraction.
\(\frac{x^2\ }{49}+\frac{{(y-3)}^2}{b^2}=1\)
Finally, take half the height to find the value for \(b\). Since half of 10 is 5, substitute 5 for \(b\). Square this value after substituting it into the general equation to get a denominator of 25 in the second fraction. Therefore, the equation of the ellipse for Charlotte’s swimming pool is:
\(\frac{x^2\ }{49}+\frac{{(y-3)}^2}{25}=1\)

