Diagonals of Parallelograms, Rectangles, and Rhombi
Hi, and welcome to this video on diagonals! Today we’re going to explore the diagonals of parallelograms, rectangles, rhombi, and squares, and see how these shapes relate to each other overall. Let’s get started!
All of the shapes that we are going to look at today are quadrilaterals, meaning they are all four-sided polygons. A polygon is a shape with multiple sides.
Types of Quadrilaterals
Properties of a Parallelogram
A parallelogram is a quadrilateral that has two sets of parallel sides. The blue arrows denote which sides are parallel to each other. The opposite sides of a parallelogram, marked by green tick marks, are congruent, which means they have the same measure.
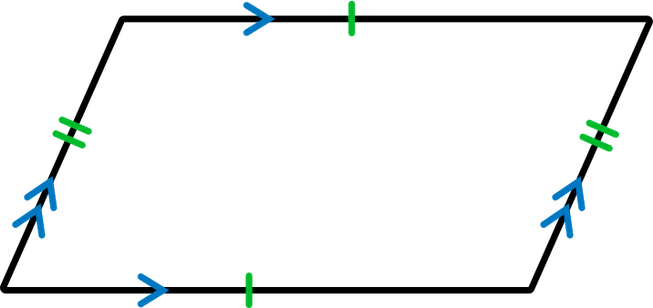
Properties of a Rectangle
A rectangle is a shape we all know well since it appears in the real world so often. But one thing we don’t usually think about is that rectangles are just a special kind of parallelogram. That means that the opposite sides are both parallel and congruent, just like our first parallelogram. What makes a rectangle a special parallelogram is that its interior angles are the same. In fact, they are all right angles, which means they measure 90 degrees.
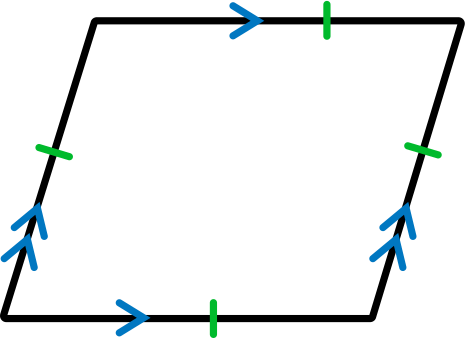
Properties of a Rhombus
Another special parallelogram is a rhombus. It has all the properties of the parallelogram but all of the sides of a rhombus are congruent. Note that the tick marks are all the same, which tells us that all the sides are the same length.
Properties of a Square
Our last special parallelogram is a rectangle and a rhombus at the same time, so it has the right angles of the rectangle and the congruent sides of the rhombus. It’s another shape we all know well: the square!
As you can see, the opposite sides are parallel, all the angles are right angles, and all the sides are congruent.
So let’s recap our quadrilaterals before we start exploring their diagonals:
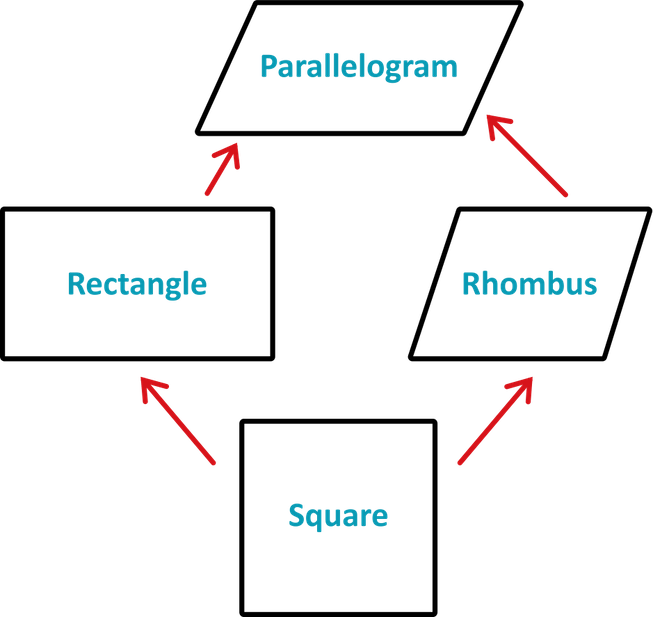
Here, we’ve arranged our quadrilaterals into a sort of “tree”, starting with the square as the trunk. Every square is a rhombus and every rhombus is a parallelogram. Every square is also a rectangle and every rectangle is a parallelogram. That’s how it works going up the tree. But it doesn’t work going down. Not every parallelogram is a rectangle and not every rhombus is a square.
Okay, now let’s explore the diagonals of these four quadrilaterals. A diagonal is a line segment connecting opposite vertices, or corners, of a quadrilateral.
Diagonals of a Parallelogram
Here’s our regular, non-special parallelogram with the diagonals shown:
As you can see, the diagonals of a parallelogram bisect each other. In other words, they cut each other in half. We could add some numbers to illustrate this better…
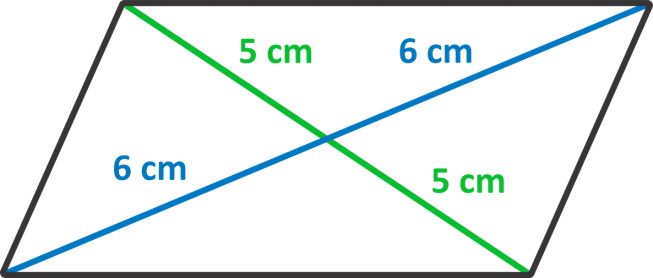
or we could use tick marks to show that the diagonals have been bisected:
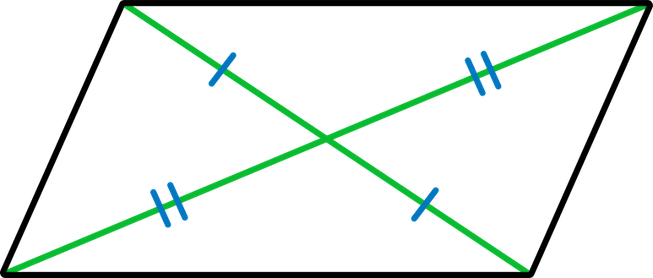
Since the three special quadrilaterals we’re talking about are all parallelograms, they will all have bisecting diagonals.
Diagonals of a Rectangle
Now let’s look at the rectangle. Here’s a rectangle with its diagonals:
The diagonals of a rectangle are congruent, and, again, since a rectangle is a parallelogram, the diagonals bisect each other, making each half the same length:
Each diagonal of a rectangle also divides the rectangle into two congruent right triangles:
This means that, if we wanted to, we could calculate the length of the diagonal using the Pythagorean Theorem.
Diagonals of a Rhombus
Now that we’ve got rectangles figured out, let’s see what happens with another special parallelogram, the rhombus:
Once again, since every rhombus is a parallelogram the diagonals bisect each other. The diagonals are NOT the same size though, so what’s special about this one? Take a look at the angles at which the diagonals intersect. These angles look like they could all be the same, and since there are four angles there it must mean…
That each angle is 90 degrees! This means that the diagonals of a rhombus are perpendicular to each other in addition to bisecting each other.
Diagonals of a Square
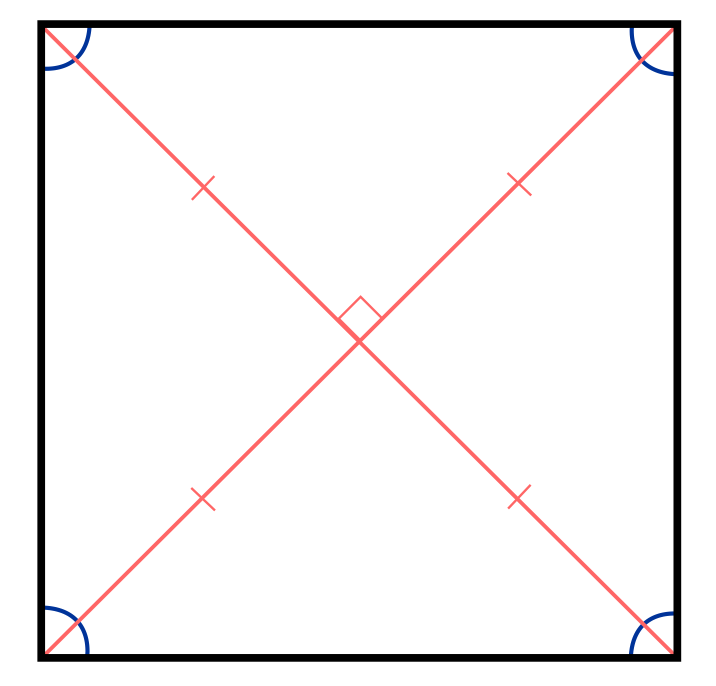
Okay, only one quadrilateral left, the square. Remember, the square is a parallelogram, a rectangle, and a rhombus, so it should have all the properties of those shapes:
- The diagonals will bisect each other.
- The diagonals will be the same length.
- The diagonals will be perpendicular to each other.
Let’s see if we’re right:
We were right! If we look closely, we can also see that the two diagonals cut the square into four congruent isosceles right triangles.
Review
Now that we’ve looked at our four parallelograms and their diagonals, let’s finish with a review to see what all you can remember.
Which of the following statements is false?
- Every rectangle is a parallelogram.
- Every rhombus is a square.
- Every square is a rectangle.
- The diagonals of a parallelogram bisect each other.
- The diagonals of a rhombus intersect at right angles.
- A diagonal of a rectangle divides it into two congruent right triangles.
- The diagonals of a rectangle are the same length.
- A quadrilateral whose diagonals bisect each other, intersect at right angles, and are congruent must be a square.
Thanks for watching, and happy studying!
Practice Questions
Which statement is false, regarding the diagonal lines drawn through a square?
The diagonal lines will be the same length.
Four congruent isosceles right triangles will be formed.
The diagonal lines will bisect each other.
Four scalene triangles will be formed.
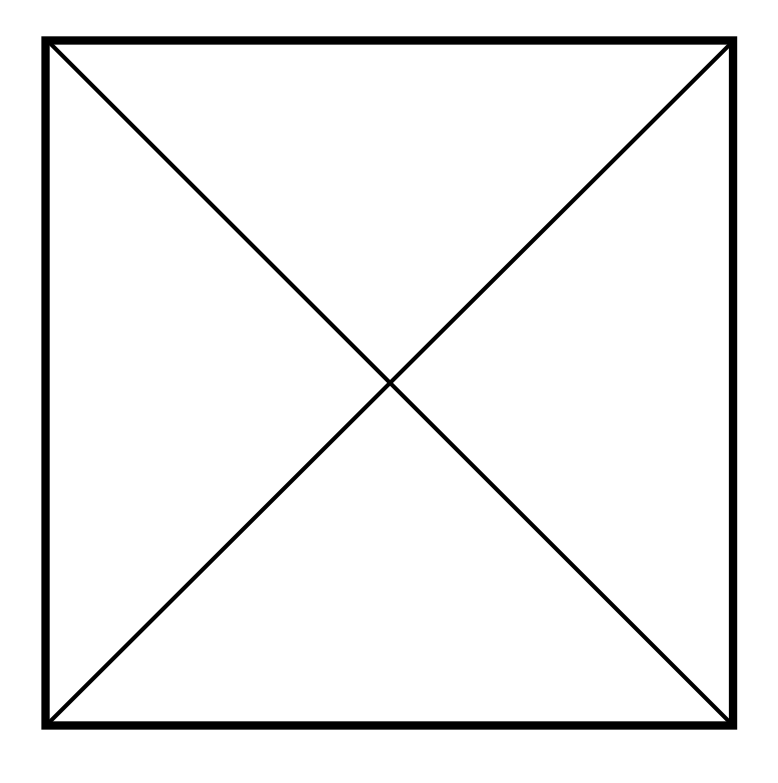
When diagonal lines are drawn through a square, three things will be true: the diagonal lines will bisect each other at their midpoints, the diagonal lines will be the same length, and the diagonal lines will create four congruent triangles that are all right isosceles triangles. Four scalene triangles will not be a result of diagonal lines drawn through a square.
Which statement is correct?
A parallelogram is always a rectangle.
A rectangle is always a square.
A rhombus is always a parallelogram.
A parallelogram is always a rhombus.
It is true that a rhombus is always a parallelogram. A rhombus has four congruent side lengths, with diagonal lines that are perpendicular to each other. Every square is a rhombus, but not every rhombus is square.
Which definition is not accurate for the shape below?
Rectangle
Quadrilateral
Rhombus
Parallelogram
This shape can be classified as a rectangle, quadrilateral, or parallelogram. However, this is not a rhombus. A rhombus has all side lengths congruent.
Sir John Boys’ House is a historical building in Canterbury. The building is now famous for its uniquely slanted red front door. A carpenter wants to document some of the measurements of the door. Which statement will be true about two diagonal lines measured across from corner to corner?
Both of the diagonal lines will be the same length.
The diagonal lines will bisect each other at the midpoint of each line.
The diagonal lines will bisect to form 90 degree angles.
The diagonal lines will create four right triangles.
The diagonal lines of a parallelogram will bisect each other at the midpoint of each line. This means that each line will be cut in half by the other line.
A hail storm has damaged the rectangular shutters on Sean’s house, so he wants to make some repairs. Before he begins the repair job, he wants to make a few measurements. Which statement about the diagonal lines drawn across the windows is incorrect?
The diagonal lines will create four 90 degree angles in the center of the window where they bisect.
Both diagonal lines will be congruent.
The diagonal lines will bisect each other at the midpoint of each line.
Each of the diagonal lines divides the rectangle into two congruent right triangles.
If the window frame was a square or a rhombus, the bisecting diagonals would create four 90 degree angles in the center of the window. However, this particular window frame is a rectangular parallelogram, so the bisecting diagonals will not create 90 degree angles.
