Finding Tangent

Hi, and welcome to this video on tangent! The word tangent has two different meanings in math. In geometry, it is used to denote when an object is touching another object at only one point, like when a line touches a circle at only one point.

We’re not concerned with that one today. Today we’re exploring tangent in trigonometry, where it is one of the “big three” trigonometric functions, along with sine and cosine. Like those two functions, it can be used to find the measure of a side or the measure of an angle in a right triangle. But it’s also a bit different than those two. It has a very different looking graph and a trig “identity” that makes it especially useful. There’s a lot to look at, so let’s get started!

We can use tangent to find the length of the side of a right triangle that is adjacent to an acute angle with a known measure as long as we know the measure of the side opposite that angle. We can also use it to find the opposite side if we know the adjacent side and the angle in question. The thing we don’t need to know to use tangent is the length of the hypotenuse, which is needed when using sine and cosine.

Tangent, which is commonly abbreviated to three letters as T-A-N, is the ratio of the side opposite the angle we know, or want to know, over the side adjacent to that angle. The adjacent side is the one touching the angle that is NOT the hypotenuse, which is the side opposite the right angle. We can write a simple equation for tangent like this:

If you’ve studied trigonometry before you’re probably familiar with SOH-CAH-TOA, which is a way to remember how each of the “big three” trig functions are formed. The third part of it, TOA, helps us remember that Tangent is equal to the length of the Opposite side divided by the length of the Adjacent side.

Tangent Formula
 
\(\text{tan }θ=\frac{\text{opposite}}{\text{adjacent}}=\frac{\text{o}}{\text{a}}\)

Let’s look at an example problem so we can put this all together.

Here, we know an angle and the side adjacent to that angle. We don’t know the length of the hypotenuse or the length of the opposite side, so it’s labeled with an x. This x is what we want to figure out.

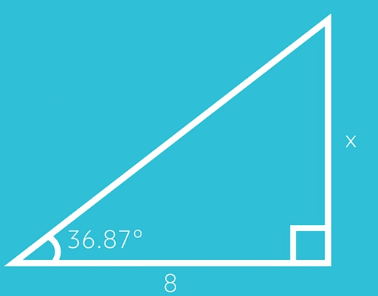
First, let’s take our equation and input our three values:

The tangent of the angle we know, 36.87 degrees, is equal to the length of the opposite side, which we’re trying to find, over the length of the adjacent side, which is eight. From here we can find the tangent of 36.87 degrees on a calculator. We type in 36.87 and hit the TAN key to find that it is equal to 0.75000279, which we can round to 0.750. So now our equation looks like this:

Multiplying both sides by 8 results in 6.000 equals x. So the measure of the opposite side is six!

Now that we know this, we could find the rest of the measures of this triangle. We could find the hypotenuse by using the Pythagorean Theorem or by using sine or cosine, and we could find the third angle by adding the two we know, 36.87 degrees and 90 degrees and subtracting from 180 degrees.

Now, tangent functions, just like sine and cosine functions, are something that we can graph. But you’ll notice that the tangent function looks different from the cosine and sine functions. Those two look like horizontal waves, like this:

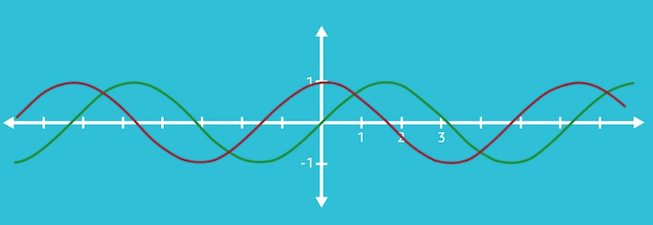
The sine wave is shown in green and the cosine wave is in red. They look the same but are out of phase with each other. The tangent wave, however, does not look like these at all.

Here’s what the Tangent function looks like:

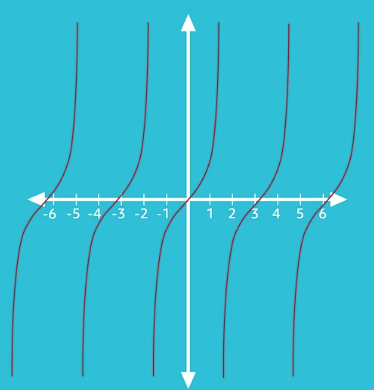
Unlike the basic sine and cosine functions, which have a range of negative one to positive one, the y-values of the tangent function have a range of negative infinity to positive infinity!

There’s something else here that is interesting. Let’s look at where the graph touches the x-axis. It crosses at x = 0 and to the right it crosses again a bit after 3 and a bit more after 6. If we were to zoom in we would see that it crosses at pi and two pi! To the left of the y-axis it crosses at x equals negative pi and x equals negative two pi.

So what’s happening in between the vertical waves? It turns out there are these invisible vertical lines called asymptotes that indicate where the graph has no points. Here’s the same graph with the asymptotes unveiled as dashed blue lines:

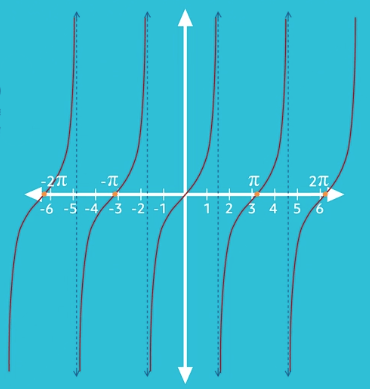
The asymptotes appear when our function y equals tan x is undefined. These asymptotes appear at x equals one half pi, at x equals one and a half pi, and so on. This happens because on one side of the asymptote the graph is approaching positive infinity and on the other side it’s approaching negative infinity, and it can’t be both!

Another way to illustrate this is to look at this tangent identity:

So, not only is tangent equal to opposite over adjacent like we talked about before, it’s also equal to sine over cosine! If we remember the graph of cosine, it has points where it has a y value of zero.

At those points this tangent identity would be trying to divide by zero, which is undefined. Your calculator will probably display “error” if you try it!

This is how you know you’ve found an asymptote. We can also use this tangent identity to solve trigonometric identity puzzles, but we’ll get into those another time.

Okay, before we go, let’s review some of the details:

Tangent is the ratio of the side opposite the angle we know, or want to know, over the side adjacent to that angle, which gives us the equation:

We use tangent to find the length of the side of a right triangle that is adjacent to an acute angle with a known measure as long as we know the measure of the side opposite that angle. When we graph tangent functions, we see that the y-values have a range of negative infinity to positive infinity, with vertical asymptotes indicating where the graph has no points.

I hope this review was helpful! Thanks for watching, and happy studying!

• “Introduction to the 6 Trigonometry Functions – Math Open Reference.” 2011. Mathopenref.com
• “Tangent – Math Open Reference.” n.d.

Tangent Practice Questions