
Trigonometry, which in Greek roughly means “triangle measure,” is a branch of mathematics that studies the relationships between the side lengths and the angles of triangles.
Cosine is one of the “big three” trigonometric functions, along with sine and tangent. Its primary use is finding the length of the side of a right triangle that is adjacent, or connected to, an acute angle with a known measure.
Today, we’re going to dig deeper into what cosine functions are all about and take a look at some problems where you’ll find one.
Let’s get started!
Example Problem #1
Let’s jump right in and give it a try with this example problem.
Cosine, which is commonly abbreviated to three letters as C-O-S, is the ratio of the side adjacent the angle we know, or want to know, over the hypotenuse of the right triangle. Remember that the hypotenuse is the longest side and is always opposite the right angle, which is the largest angle in any right triangle. And a ratio is just a fraction, so we can write it like this:
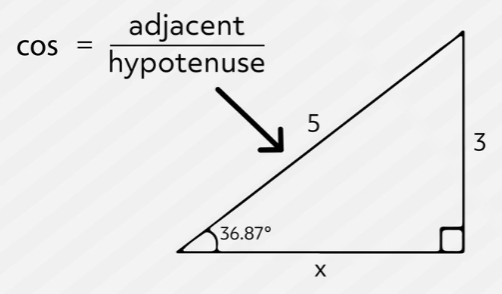
If you’ve studied trigonometry before, you’re probably familiar with “SOHCAHTOA,” which is a way to remember how each of the big three trig functions are formed. The second part of it, CAH, helps us remember that Cosine is equal to the length of the Adjacent side divided by the length of the Hypotenuse.
\(\text{cos }θ=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{\text{a}}{\text{h}}\)
In this problem, we know one angle and two of the sides. The side we don’t know is adjacent to the angle we know, so we need to use cosine to find it. We do so by setting up a simple equation, like this: cosine of 36.87 degrees is equal to x over 5.
The cosine of the angle we know, 36.87 degrees, is equal to the length of the adjacent side, which we’re trying to find, so we use a variable over the length of the hypotenuse, which is 5.
From here, we can find the cosine of 36.87 degrees on a calculator. We type in 36.87 and hit the COS key to find that it is equal to 0.799, which we can round to 0.800. So now our equation looks like this: \(0.8 = \frac{x}{5}\).
Multiplying both sides by 5 results in \(4.000 = x\). So the measure of the adjacent side is 4!
You may have recognized that this is a 3-4-5 special right triangle, since the hypotenuse is 5 and the other two sides measure 3 and 4. We see this special triangle often in standardized tests, so it’s a good idea to try to recognize them when they appear. Note that the sides can also be multiples of 3-4-5, so 6-8-10 or 9-12-15 triangles are also 3-4-5 right triangles.
Example Problem #2
Okay, back to cosine! We can also use cosine to find an angle of a right triangle if we know the length of the adjacent side and the length of the hypotenuse, which is always the side opposite the right angle. Let’s try one of those:
Let’s see what we know. It’s a right triangle, so trigonometry can definitely be used. We’re trying to find an angle, since it’s marked with an x. We know the hypotenuse, which is 13, and we know the side that is adjacent to that angle we want to know. Since we know the adjacent side and the hypotenuse, that means we need to use cosine. Let’s set up our equation: \(\text{cos }θ=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{\text{a}}{\text{h}}\).
So, \(\text{cos }x=\frac{12}{13}\).
In the first problem we did, we took the cosine of an angle and the calculator gave us a number. For this problem, we want to do the opposite. We know the value of the cosine of our angle and want to find the measure of the angle.
So what we need is the ARC COS, which is often labeled as ACOS or, even more commonly, as COS to the negative 1 power, or COS inverse, as you’ll see on most HP calculators. This is the inverse operation of COS. This is accessed by hitting the 2nd key and then the COS key.
Okay, so we type in 12 over 13 and then 2nd and then COS and our calculator displays 22.619, or approximately 22.62 degrees. We’ve found our answer. That answer makes sense when looking at our triangle. It’s important to remember that you should only trust the proportions of the diagram if it is drawn to scale. On standardized tests it will often be indicated if the drawing is not to scale.
Example Problem #3
Cosine functions can also be graphed. Let’s set up a graph of the basic cosine function.
This is a cosine wave. It looks a lot like the more famous sine wave, but it’s phase-shifted by pi over 2 radians. Let’s overlap the cosine and sine functions so we can see the shift:
We can clearly see that they have the same shape. The sine wave in green starts with a \(y\)-value of 0 when \(x\) is 0, while the cosine wave starts with a \(y\)-value of 1. Just like a sine wave, a cosine wave has a maximum \(y\)-value of 1 and it’s minimum \(y\)-value is -1. This is true when the cosine or sine function hasn’t been modified.
We can change the height, or the amplitude, of these functions by multiplying them by a coefficient, like this: \(y = 2 cos x\).
This will simply double the \(y\)-values of our base function \(y = cos x\).
Let’s take a look at this with our original cosine function in red and our height-doubled cosine function in blue.
We can see that our functions have the same frequency, which means that they have the same period, or distance between their peaks. But the two graphs do have a different amplitude. The blue graph is stretched vertically and has \(y\)-values as high as 2 and as low as -2, just as we’d expect.
And that’s all there is to it! As you can see, cosine comes in handy when graphing, solving problems with angles, and determining trigonometric identities. Thanks for watching, and happy studying!
Cosine Practice Questions
What is the length of one leg of an isosceles right triangle where the hypotenuse is 9 cm?
Since we know that an isosceles triangle has two congruent sides and this triangle is a right triangle, we can conclude that the measure of each base angle is 45°. We can set up our equation as \(cos(45) = \frac{x}{9}\). To simplify we find the value of \(cos(45)\) which is 0.7071. We can multiply \(0.7071\times9 = x\); therefore, \(x=6.36\).
Triangle ABC is a right triangle where Angle A is 55° and Angle C is 35°. The length of Side AB is 8.6 cm and the length of Side BC is 12.3 cm. Use cosine to find the length of the hypotenuse. (Round your answer to the nearest whole number.)
Since we know that \(cos(Θ)=\frac{a}{h}\) , we will start filling in the information we have. We can use either \(cos(55°)=\frac{8.6}{h}\) or \(cos(35°)=\frac{12.3}{h}\) and then solve for h, which is the hypotenuse. Therefore, \(h=\frac{12.3}{cos(35°)}\) or \(h=\frac{8.6}{cos(55°)}\), which rounded to the nearest number equals 15 cm.
Triangle PQR is a right triangle. The length of Side PQ is 8 inches, the length of Side QR is 15 inches, and the length of Side PR is 17 inches. What is the measure of Angle R? (Round your answer to the nearest whole number.)
To find the measure of an angle we use arc cosine; therefore, arc cos\((x)=\frac{15}{17}\), where x, is the measure of Angle R. We will solve this by finding the ratio of adjacent to hypotenuse then using the arc cos button on the calculator which will give us approximately 28°, the measure of Angle R.
Johan travels 12 miles north from his house to a forest. When leaving the forest, he takes the wrong turn and travels 13 miles southeast, as shown on the diagram.
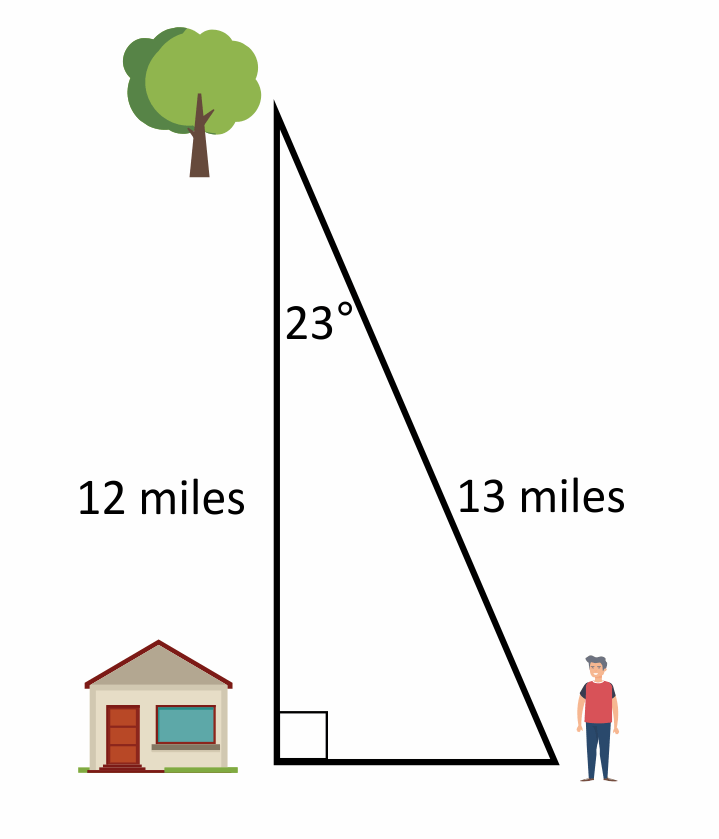
What is Johan’s current distance from his house?
The angle on the diagram where Johan is standing is \(90°-23°=67°\). Therefore, \(cos(67°)=\frac{x}{13}\). We will solve for x by multiplying both sides by 13, which is \(13(0.391)=x\), and \(x=5.1\) miles.
In the right triangle LMN, the length of the hypotenuse LN is 25 meters and measure of Angle L is 20°. What is the approximate length of Side LM?
Since the angle adjacent to Side LM is 20°, we can set up the equation \(cos(20°)=\frac{x}{25}\). We will multiply both sides by 25 to get \(25(0.9397)=x\), and x is approximately 23.5 meters, which is the length of Side LM.