
Hello, and welcome to this video about pyramids! In this video, we will explore different types of pyramids and how to calculate their volume and surface area. Let’s learn about pyramids!
Historical Pyramids
We cannot talk about pyramids without mentioning the most famous pyramids in the world, located in Egypt, and built as a tomb for Egyptian kings. Although pyramids are not quite common, their shape is so striking that it seems it is used to make a statement, perhaps that is the reason the Egyptian kings used it as their tomb. The Louvre Museum in Paris, which is the largest art museum in the world, is also shaped like a pyramid.
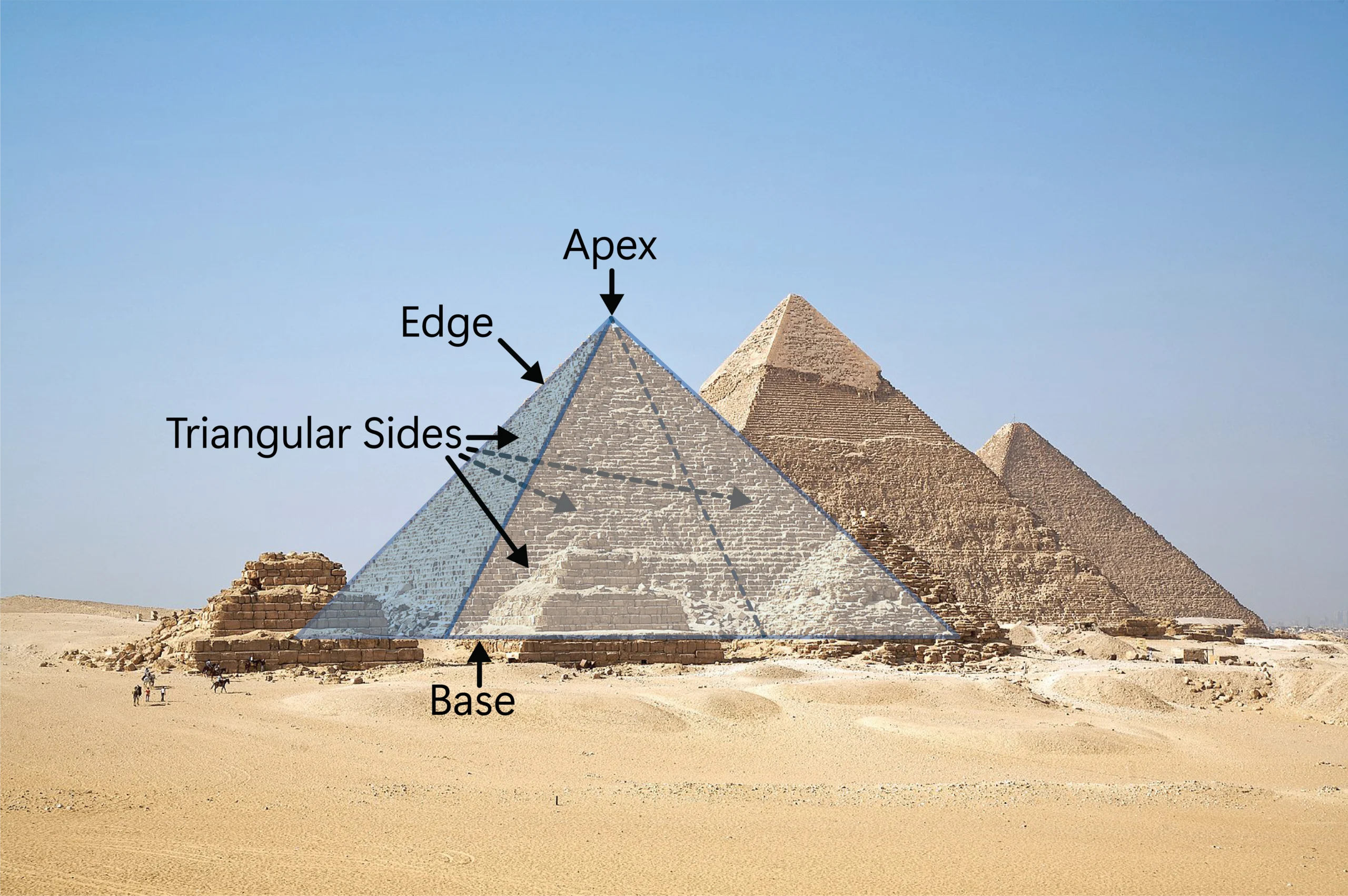
Pyramids in Geometry
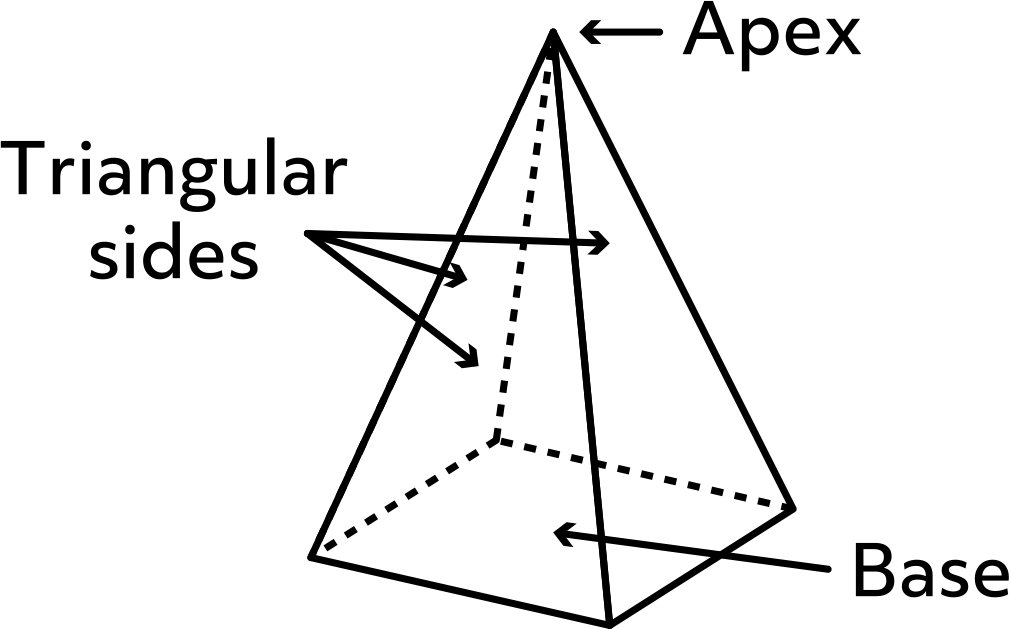
As you can see from the images of the Egyptian Pyramids, a pyramid is a 3-dimensional figure with triangular sides that meet at the edges and at the top to form an apex and it has a polygon as its base.
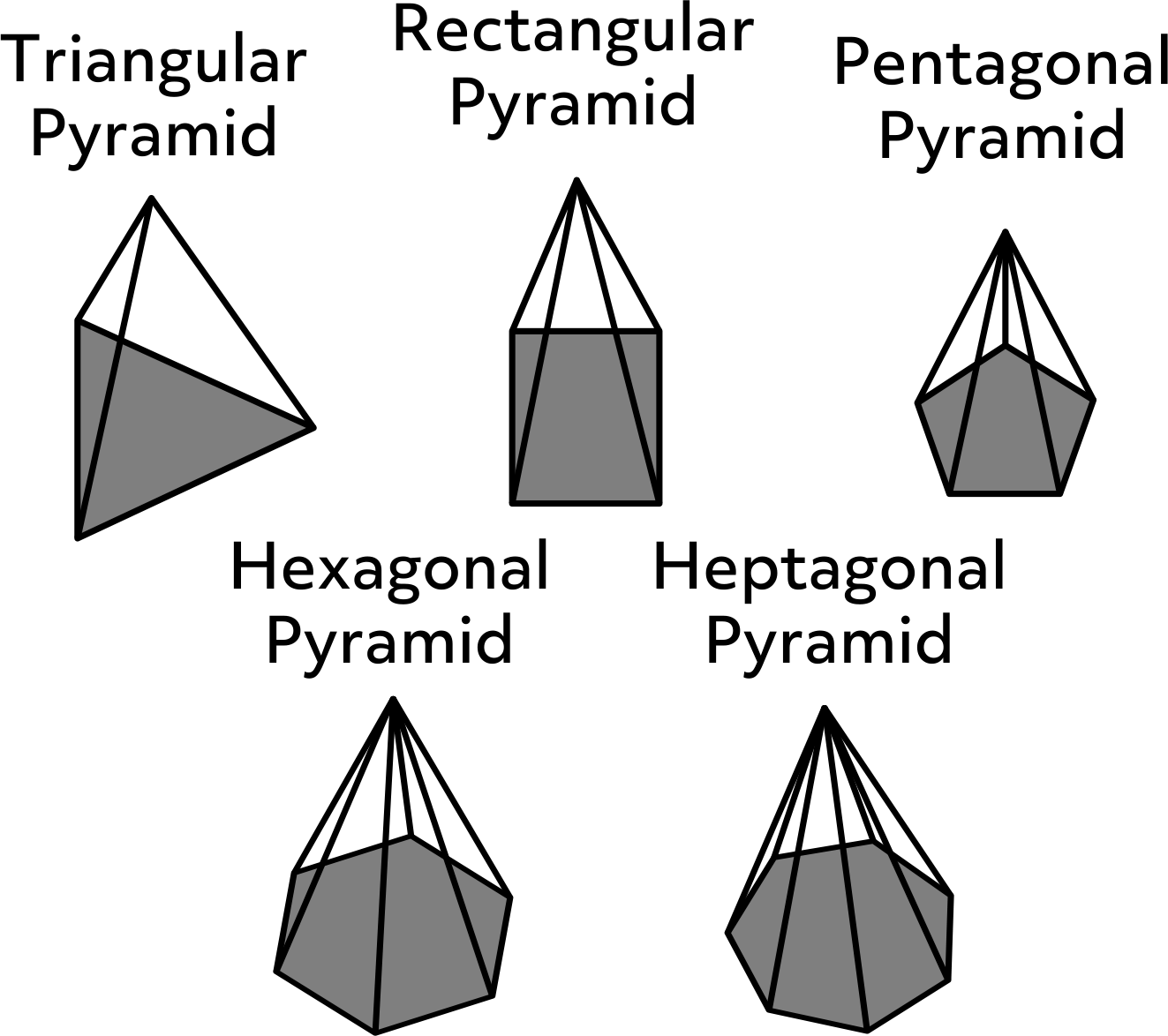
The polygonal base determines the type of pyramid. Here you see the pyramid with a triangle as its base is a triangular pyramid, the pyramid with a rectangle as its base is a rectangular pyramid, and the pyramid with a pentagon as its base is a pentagonal pyramid. We also have hexagonal pyramids and heptagonal pyramids, and so on.
Let’s take a moment and recall what the volume and surface area of a 3-dimensional figure means.
Volume and Surface Area Formula
The volume of a 3-dimensional figure is the measure of how much it can hold, and it is measured in cubic units.
The surface area of a 3-dimensional figure is the measure of the total area that the surface of the figure covers and is measured in square units.
Before we can calculate the volume and surface area of a pyramid, we must know the difference between the height and slant height. The height of a pyramid is the perpendicular length from the apex to the base, and the slant height is the length from the apex to the midpoint of the bottom edge of one of the triangular faces.
Here are the formulas for the volume and surface area of any pyramid.
\(SA=B+\frac{1}{2}ps\)
To calculate the volume and surface area of any pyramid we need B, which represents the area of the base, and p, which represents the perimeter of the base. It is important to note, since the base of a pyramid can be any polygon, we will be using our prior knowledge of finding the area and perimeter of different polygons to calculate the volume and surface area of a pyramid.
\(SA=B+\frac{1}{2}ps\)
\(h\) = height of pyramid
\(p\) = perimeter of base
\(s\) = slant height
Let’s look at an example.
Calculating Surface Area – Example 1
A triangular pyramid has an equilateral triangle as its base with side lengths 6 in and a height of 8 in.
To find the surface area of a pyramid, we use the formula \(SA=B+\frac{1}{2}ps\), where \(B\) is the area of the base, \(p\) is the perimeter of the base, and \(s\) is the slant height. Since the base is a triangle, we will use the formula for the area of a triangle to find \(B\).
\(\text{Area of a triangle}=\frac{1}{2}bh\), where the \(b\) and \(h\) are the base and height of the triangular base. We will draw a perpendicular line to the base, which is the height of the triangular base and it divides the base of the triangle into 2 equal parts. Since the triangle is now turned into 2 right triangles, we can use the Pythagorean theorem to find the height.
So the Pythagorean theorem is:
And then we’re gonna look at our triangle, which says we have:
\(36=h^{2}+9\)
We’ll subtract 9 from both sides. This gives us:
And then we’ll square root both sides. Which gives us:
OR
\(h\approx 5.2\)
Therefore, the area of the base can be found by doing:
\(A=\frac{1}{2}(6)(5.2)\)
\(A\approx 15.6 \text{ in}^{2}\)
The perimeter of the base is equal to all the sides added together, so:
Now to solve for surface area, all we have to do is plug these values in for our variables. So our surface area is equal to:
\(SA=(15.6)+\frac{1}{2}(18)(7)\)
\(SA\approx 78.6 \text{ in}^{2}\)
And all this added together is approximately equal to 78.6 square inches.
Calculating Volume – Example 1
To find the volume of the triangular pyramid, we need the area of the base, \(B\), and the height of the pyramid, which is 8 inches. So let’s plug this in. So:
\(V=\frac{1}{3}(15.6)(8)\)
Now all we have to do is calculate this out, which is equal to approximately 41.6 cubic inches.
Let’s look at another example.
Calculating Volume – Example 2
Here is a pyramid with a square base, with side lengths of 5 centimeters. The height of the pyramid is 11 centimeters. What is the volume of the pyramid?
So our volume formula is:
Before we can calculate the volume of the pyramid, we need to find the area of the base. Since the base is a square, we use the formula for the area of a square, which is \(s^{2}\). So to find our area, we’re gonna use \(s^{2}\) and our side length is 5.
\(A=(5)^{2}\)
\(A=25\text{ cm}^{2}\)
Now we can plug this value into our formula.
\( V=\frac{1}{3}(25)(11)\)
\(V\approx 91.67\text{ cm}^{3}\)
Then if we plug this into a calculator, we’ll get that it’s approximately equal to 91.67 cubic centimeters.
But when would we ever need this in real life? Well, I’m glad you asked! Take a look at this next example and try it on your own.
Calculating Surface Area – Example 2
The roof of a wooden cottage is shaped like a square-based pyramid. The length of the sides of the square base are 22 feet and the height of the triangular face is 14 feet. Peter wants to paint the roof of his wooden cottage and needs to determine how much paint he needs to buy. We will assume 1 pint of paint covers 400 square feet. How much paint does Peter need to buy?
The roof of the cottage does not include the base of the pyramid. Therefore, we only need to find the area of the 4 triangular faces. This is called the lateral area. So the lateral area is equal to the surface area minus the area of the base. So all we need is:
The perimeter of our square is equal to 4 times the side length.
Which we can plug into a calculator to get:
So we will need 616 square feet to be covered.
If 1 pint of paint covers 400 square feet, we need to divide 616 by 400 to figure out how much paint we need. So:
So, Peter will need to buy 2 pints of paint to cover the roof of the cottage because 1 pint won’t be enough and you can’t get 0.54 of a pint. So 2 pints of paint will cover the whole roof.
I hope this video on finding the volume and surface area of a pyramid was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you find the volume of a pyramid?
A
To find the volume of a pyramid, we multiply the area of its base with the height of the pyramid, and divide by \(3\). We express this product with the formula \(V=\frac{1}{3}\times B\times h\), where \(B\) is the area of the base of the pyramid, and \(h\) is its height.
Example: A triangular pyramid has a height of \(9\text{ cm}\), and a base area of \(20\text{ cm}^2\). So its volume is \(\frac{1}{3}\times20\times9=60\text{ cm}^3\).
Q
Why is there a \(\frac{1}{3}\) in the formula for the volume of a pyramid?
A
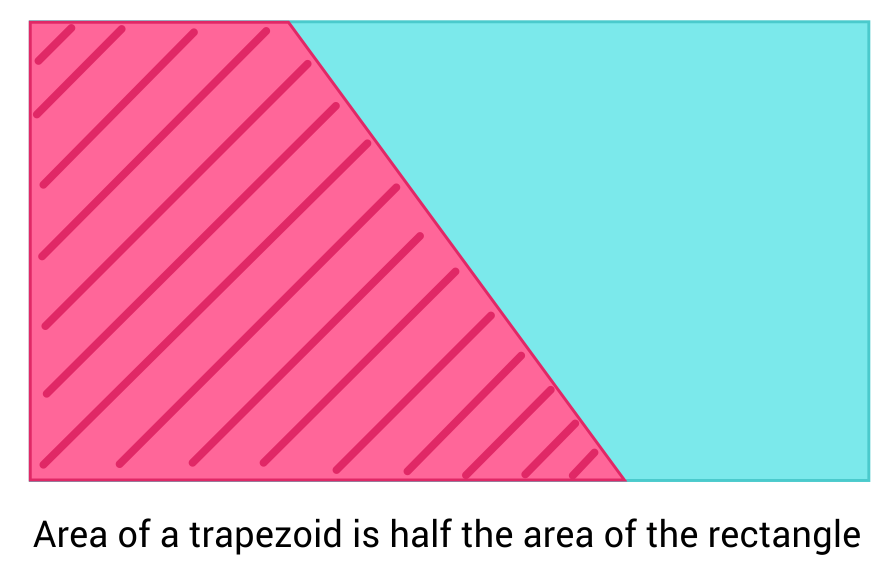
In a similar way to how we derive the area of a trapezoid by cutting a rectangle in half, we can derive the volume of a pyramid by cutting a prism into six small pyramids. We then look at half of the prism, which is then the same height as the pyramid in question, to find that the volume of our pyramid is one-third of the half-prism, or one-third the volume of a prism of the same height.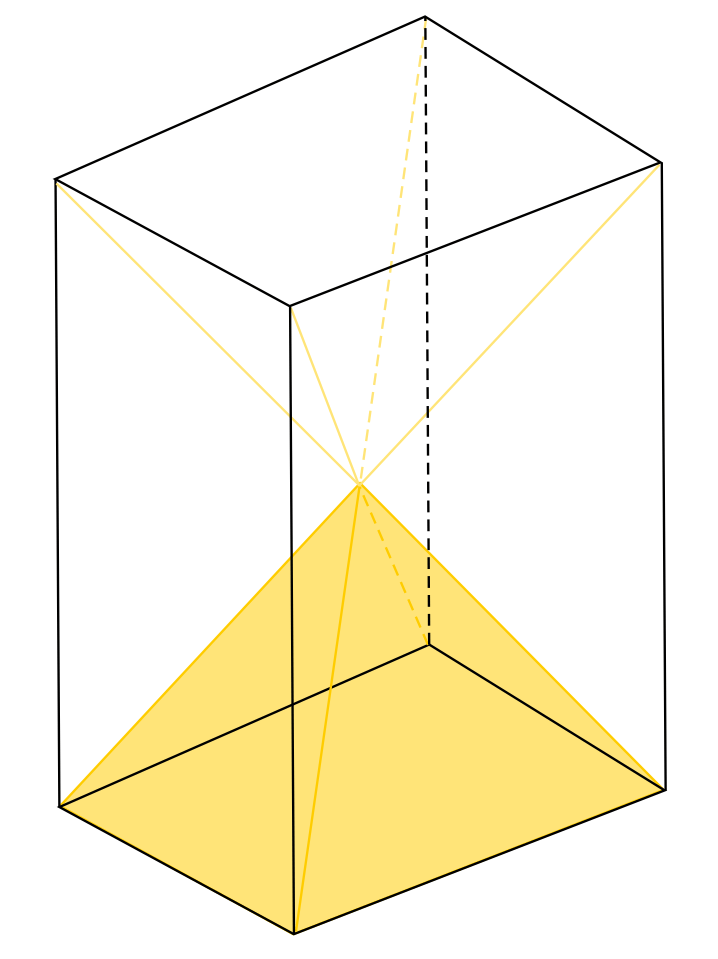
Q
What is the starting formula for volume of a pyramid?
A
The general formula for the volume of a pyramid is \(V=\frac{1}{3}\times B\times h\), where \(B\) is the area of the base of the pyramid, and \(h\) is the height of the pyramid.
Q
What is the volume of a square pyramid?
A
For pyramids whose bases are square, we can find their volume using the formula \(V=\frac{1}{3}\times s^2\times h\), where \(s\) is the length of the sides of the square base.
Example: A square pyramid has height of \(11\text{ cm}\), and base side lengths of \(6\text{ cm}\). Its volume is \(\frac{1}{3}\times6^2\times11=132\text{ cm}^3\).
Q
What is the volume of a triangular pyramid?
A
To find the volume of a pyramid whose base is triangular, use the formula \(V=\frac{1}{3}\times(\frac{1}{2}\times b_{triangle}\times h_{triangle})\times h_{pyramid}\).
The product inside the parentheses is the area of the base, which we multiply by \(\frac{1}{3}\) and the height of the pyramid.
Example: A triangular pyramid has height \(8\text{ cm}\) and its base has the following dimensions: The base area is then \(\frac{1}{2}\times10\times4=20\text{ cm}^2\). The volume of the pyramid is \(V=\frac{1}{3}\times20\times8=53.33\text{ cm}^3\).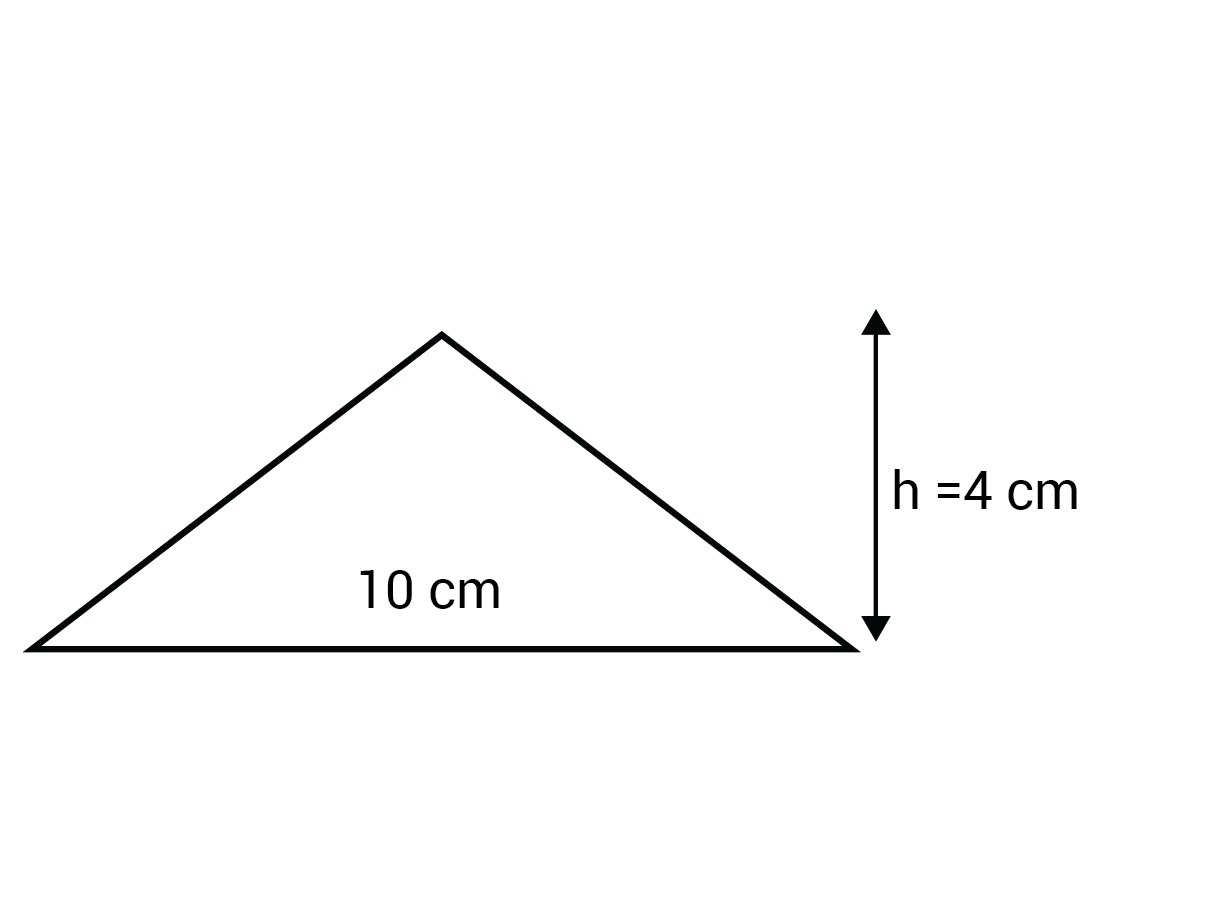
Q
What is the volume of a rectangular pyramid?
A
The formula for volume of a pyramid changes based on the shape of the pyramid’s base. For rectangular pyramids, whose base has length \((l)\) and width \((w)\), \(V=\frac{1}{3}\times l\times w\times h\). Once again, \(h\) represents the height of the pyramid.
Example: A rectangular pyramid has a base with dimensions \(5\times6\text{ cm}\), and height \(12\text{ cm}\). Its volume is \(\frac{1}{3}\times5\times6\times12=120\text{ cm}^3\).
Q
How do you find the volume of a regular pentagonal pyramid?
A
Once again, to determine the volume of a pyramid, we multiply the area of its base with its height and divide by \(3\). For pyramids whose base is a regular pentagon (that is, all five sides are equal in length and all five angles are equal as well), it is important to first determine the area of that pentagon. If you have the length \(s\) of each side of the pentagon, the area can be determined using the formula \(A_{pentagon}=\frac{1}{4}\sqrt{5(5+2\sqrt{5})}\times s^2\).
Those constants can be reduced to approximately \(1.72048\), so then \(A_{pentagon}≈1.72\times s^2\).
This leads us to the formula for the volume of a regular pentagonal pyramid: \(V≈\frac{1}{3}\times(1.72\times s^2)\times h\), where \(h\) is the height of the pyramid.
Q
How do you find the total surface area of a pyramid?
A
To find the total surface area of a pyramid, we need to add up the areas of each side, including the base. For triangular pyramids, there will be three side panels; for square and rectangular pyramids, there will be four; and so on.
Q
What is the formula for surface area of a triangular pyramid?
A
In order to find the total surface area, we will need to add up the areas of the base and the three other sides. \(SA=B+\frac{1}{2}(P\times l)\), where \(B\) is the area of the base of the pyramid, \(P\) is the perimeter of the base, and \(l\) is the slant height of the pyramid. We can find \(B\) by using the formula \(\frac{1}{2}bh\) for area of a triangle. \(P\) can easily be determined by adding up the lengths of the sides of the base triangle. Slant height \(l\) can be found using Pythagorean theorem, where \(l\) is the hypotenuse length.
Q
What is the total surface area of a square pyramid?
A
To find the total surface area of a square pyramid, we sum the area of the base with the area of the four sides. Because the four side panels are identical, we just need to find that area once, and multiply it by four.
\(SA=A_{base}+(4\times A_{side})\)
Example: Find the total surface area of a square pyramid whose base side lengths are \(8\text{ cm}\), and whose height is \(3\text{ cm}\). We begin by calculating the surface area of the base.
\(A_{base}=8\times8=64\times{ cm}^2\)
The area of each of the side panels can be found using the formula for area of a triangle, \(A=\frac{1}{2}bh\). In this case, \(h\) is the slant height, which we can find using Pythagorean’s theorem.
\(A_{side}=\frac{1}{2}\times8\times5=20\text{ cm}^2\)
Then we sum all sides’ areas together to find the surface area:
\(SA=64+4(20)=144\text{ cm}^2\).
Volume and Surface Area of a Pyramid Practice Questions
Calculate the surface area of the following square pyramid.
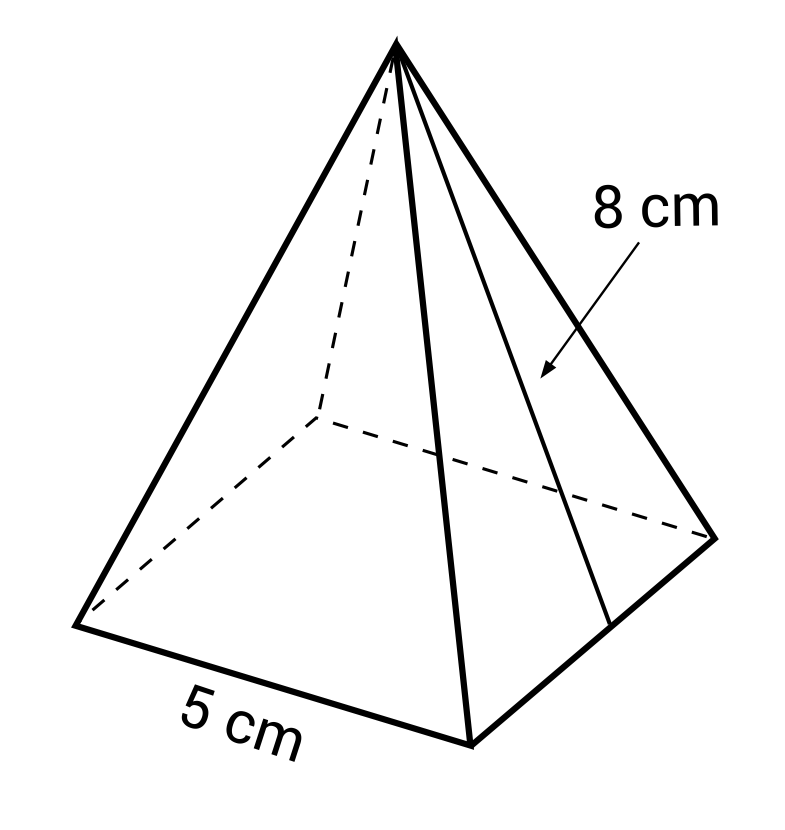
The formula \(SA=B+\frac{1}{2}pl\) can be used to calculate the surface area of a square pyramid.
\(B\) represents the area of the base.
\(p\) represents the perimeter of the base.
\(l\) represents the slant height.
When the appropriate values are plugged into the formula, \(SA=B+\frac{1}{2}pl\) becomes \(SA=25+\frac{1}{2}(20)(8)\) which simplifies to 105 cm2. The surface area of the square pyramid is 105 cm2.
Calculate the surface area of the following equilateral triangular pyramid.
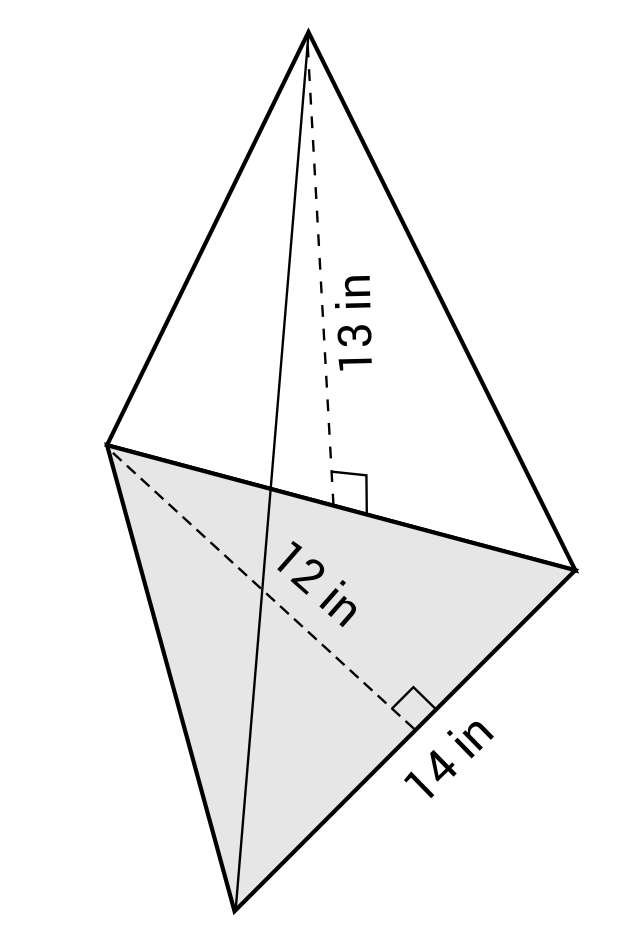
The formula for calculating the surface area of a triangular pyramid is very similar to the formula for a square pyramid. The only difference occurs when determining the area of the base shape. The formula \(SA=B+\frac{1}{2}pl\) will still apply, but B will be calculated by multiplying \(\frac{1}{2}bh\). This can be plugged into the formula for B, which results in the following: \(SA=(\frac{1}{2}bh)+\frac{1}{2}pl\). From here, we can simply plug in all of the appropriate values so that \(SA=(\frac{1}{2}bh)+\frac{1}{2}pl\) becomes \(SA=(\frac{1}{2})(14)(12)+\frac{1}{2}(42)(13)\) which simplifies to \(SA=357\text{ in}^2\). The surface area of the equilateral triangular pyramid is \(357\text{ in}^2\).
Calculate the volume of the pyramid.
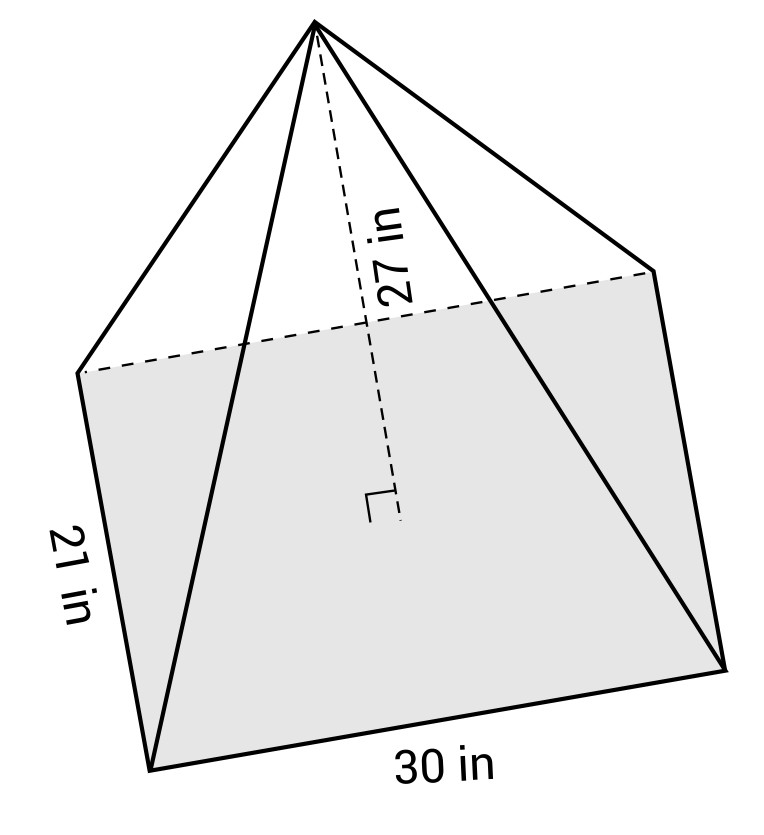
The formula \(V=\frac{1}{3}Bh\) can be used to calculate the volume of a pyramid.
B represents the area of the base shape.
h represents the height of the pyramid (not the slant height). When the appropriate values are plugged into the formula, \(V=\frac{1}{3}Bh\) becomes \(V=\frac{1}{3}(21)(30)(27)\) which simplifies to \(V=5{,}670\). The volume of the pyramid is 5,670 in3.
Leo has a triangular glass pyramid that he is hoping to fill with some beach sand. On his vacation to Florida he collects 6.5 cm3 of sand. The triangle at the base of the glass pyramid has an area of 5 cm2, and the height of the pyramid is 6 cm. If he collects 6.5 cm3 of sand, will the pyramid be large enough to hold all of the sand?

The volume of the triangular based pyramid can be calculated using the formula \(V=\frac{1}{3}Bh\) where B is the area of the base triangle, and h is the height of the pyramid. When B and h are plugged in, \(V=\frac{1}{3}Bh\) becomes \(V=\frac{1}{3}(5)(6)\) which simplifies to \(V=10\). The volume of the pyramid is 10 cm3, which is enough room for the 6.5 cm3 of sand.
Some of Leonardo da Vinci’s first sketches of parachute designs were in the shape of square based pyramids. For a parachute design with rectangular base side lengths of six feet and eight feet, and a height of seven feet, how much air would be captured in the pyramid once it is deployed fully?
The formula \(V=\frac{1}{3}Bh\) can be used to calculate the volume of a pyramid. B represents the area of the base shape, and h represents the height of the pyramid. When the appropriate values are plugged into the formula \(V=\frac{1}{3}Bh\) becomes \(V=\frac{1}{3}(48)(7)\), which simplifies to \(V=112\). The volume of the fully deployed parachute would be 112 ft3.