How to Find the Tangent Line of a Circle
Hi, and welcome to this video on tangent lines!
Today we’re going to explore what can happen when a circle and a line meet, and we’ll start by exploring how these two shapes can interact. The most a line can intersect with a circle is by crossing over it, like this:
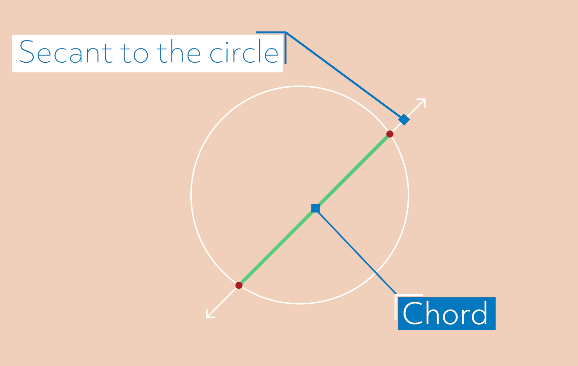
We can see that the line intersects the outside of the circle at two points and creates a line segment between those points that is called a chord. A line that cuts across a circle in this way is called a secant to the circle.
Another scenario would be a line that doesn’t intersect the circle at all, like this:
Even though the arrows on the line represent the line going on forever, it will never intersect with the circle. There really isn’t much to say about this one, but we should be aware that it can happen.
There’s one other thing that can happen with a circle and a line, and it looks like this:
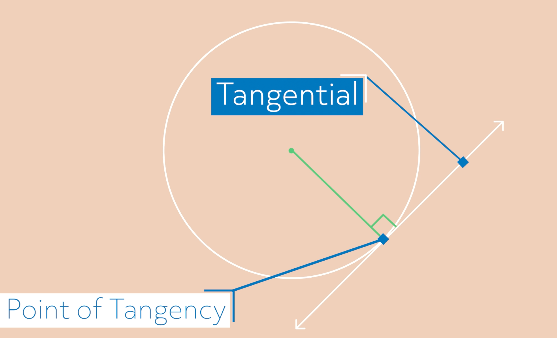
In this case, the line only touches the circle at one point. This line can be described as tangent to the circle, or tangential. The point where the line and the circle touch is called the point of tangency.
Looking closely at our diagram we can see a radius of the circle meeting our tangential line at a 90-degree angle. For our line to be truly tangent this must be true. If our line isn’t exactly perpendicular to the radius at the point of tangency it will actually touch the circle twice, though possibly very close together. We can see that with a close up that shows the angles that are just a few degrees away from 90 degrees:
Even if the angle were even closer to 90 degrees, such as 90.1° and 89.9° this would still happen, though it would be harder to show in a diagram, at least without a microscope.
Now, what if we’re given a circle with a tangent line, and we want to know the slope of the line? If we know the center of the circle and point of tangency then we can figure it out. Let’s take a look:
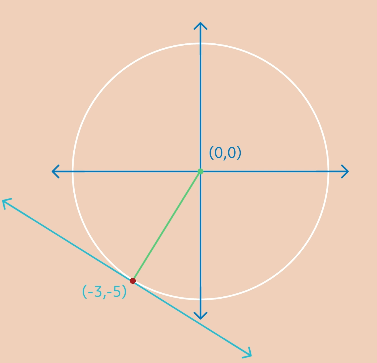
We can see that the center of the circle is at the origin, or the point (0,0), and the point of tangency is at (-3,-5). Since we have two points on the radius we can determine the slope of the radius using the slope formula:
Let’s call the center of the circle point #1 and the point of tangency point #2.
Remember, it doesn’t matter which point we call #1 or #2, just that we need to be consistent with how we substitute once we decide.
So we’ve found the slope of the radius! But that’s not the final answer because we’re trying to find the slope of the tangent line. Since the tangent line is perpendicular to the radius, we can find it by taking the negative reciprocal of the slope of the radius. Finding the negative reciprocal just means that we flip it over and change the sign. So the slope of the tangent line is -3/5.
That’s all there is to it! Thanks for watching, and happy studying!
Tangent Line of a Circle Practice Questions
In the image below, a line crosses over a circle. The line intersects the circle at exactly two points, and creates a red line segment between those two points. What is this red line segment called?
Diameter
Radius
Tangent
Chord
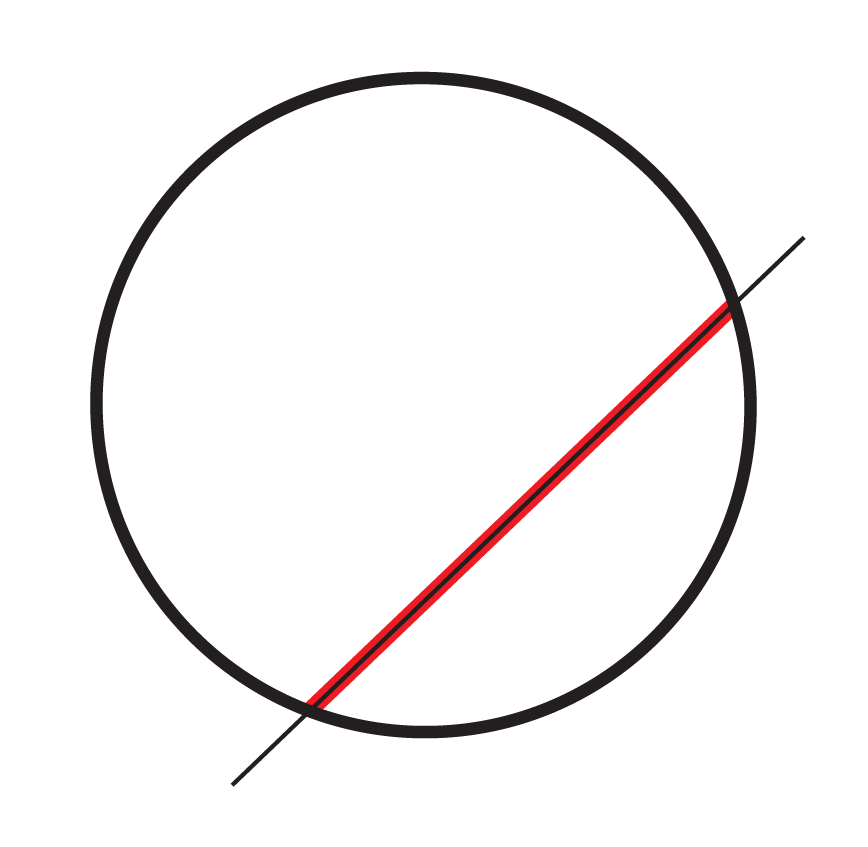
A chord is a line segment that joins two points on the circumference of a circle.
Point A is the center of the circle. Point C represents one point on the circumference of the circle. The blue line represents the radius of the circle. What is the term for the red line?
Chord
Line of tangency
Slope line
Line of radius
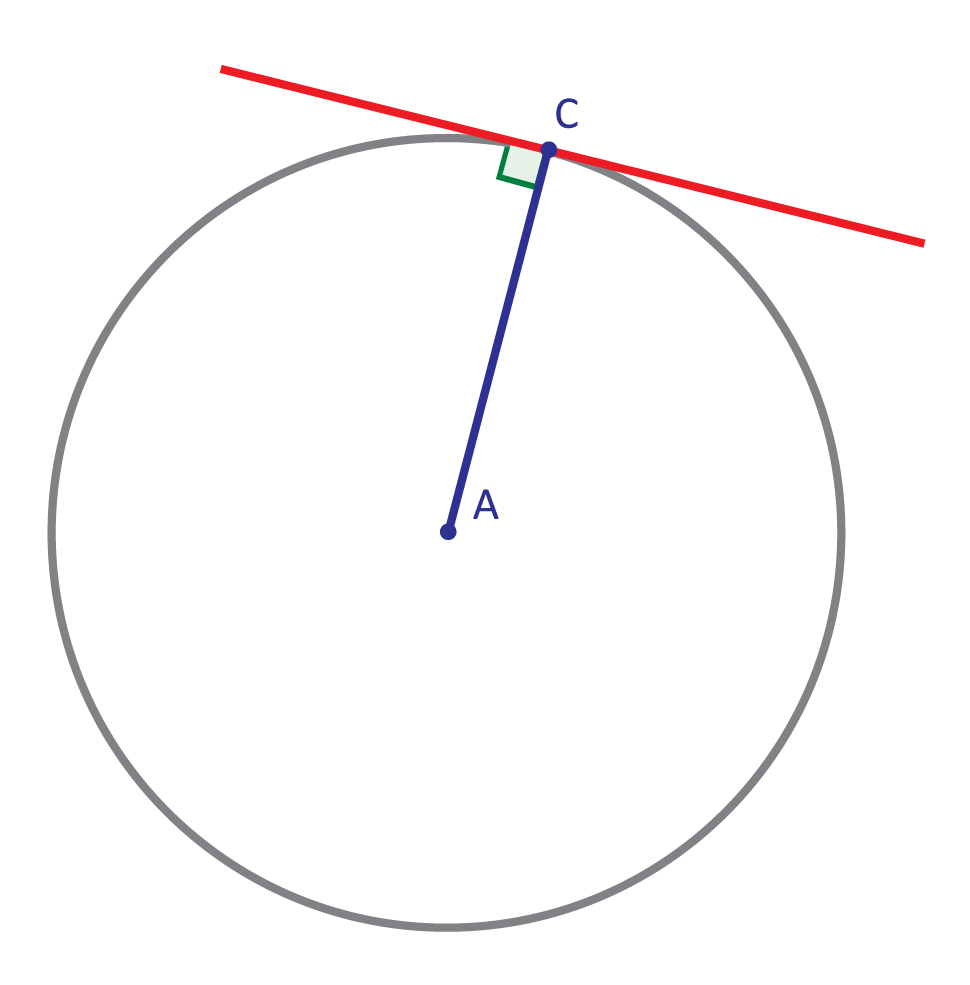
A line that contacts the circumferences of a circle in exactly one location is called a line of tangency.
Find the slope of the tangent line for a circle with a center point of \((0,0)\) and a point on the circumferences \((4,5)\).
The slope of the tangent line is \(-\frac{5}{4}\)
The slope of the tangent line is \(\frac{5}{4}\)
The slope of the tangent line is \(-\frac{4}{5}\)
The slope of the tangent line is \(\frac{4}{5}\)
To find the slope of the tangent line, we first need to find the slope of the radius formed by connecting the center point \((0,0)\) to the point on the circumference \((4,5)\). This can be done using the slope formula:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
The formula now becomes \(m=\frac{5-0}{4-0}\) which simplifies to \(\frac{5}{4}\).
The slope of the radius is \(\frac{5}{4}\). The slope of the tangent line can be determined by finding the negative reciprocal of this. In other words, flip the fraction and change the sign.
The negative reciprocal of \(\frac{5}{4}\) is \(-\frac{4}{5}\).
Find the slope of the tangent line for a circle with a center point of \((0,0)\) and a point on the circumferences \((5,1)\).
The slope of the tangent line is \(-\frac{1}{4}\)
The slope of the tangent line is \(\frac{1}{4}\)
The slope of the tangent line is \(-\frac{5}{1}\)
The slope of the tangent line is \(\frac{1}{5}\)
To find the slope of the tangent line, we first need to find the slope of the radius formed by connecting the center point \((0,0)\) to the point on the circumference \((5,1)\). This can be done using the slope formula:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
The formula now becomes \(m=\frac{1-0}{5-0}\) which simplifies to \(\frac{1}{5}\). The slope of the radius is \(\frac{1}{5}\). The slope of the tangent line can be determined by finding the negative reciprocal of this. In other words, flip the fraction and change the sign.
The negative reciprocal of \(\frac{1}{5}\) is \(-\frac{5}{1}\).
Explain why it is not possible to determine the slope of the tangent line in the example below.
The red line is not long enough to determine the slope of the tangent line.
The red line is not tangential to the circle. A tangent line would cross the circle at exactly one point.
The red line needs to cut through the middle of the circle in order to determine the slope of the tangent line.
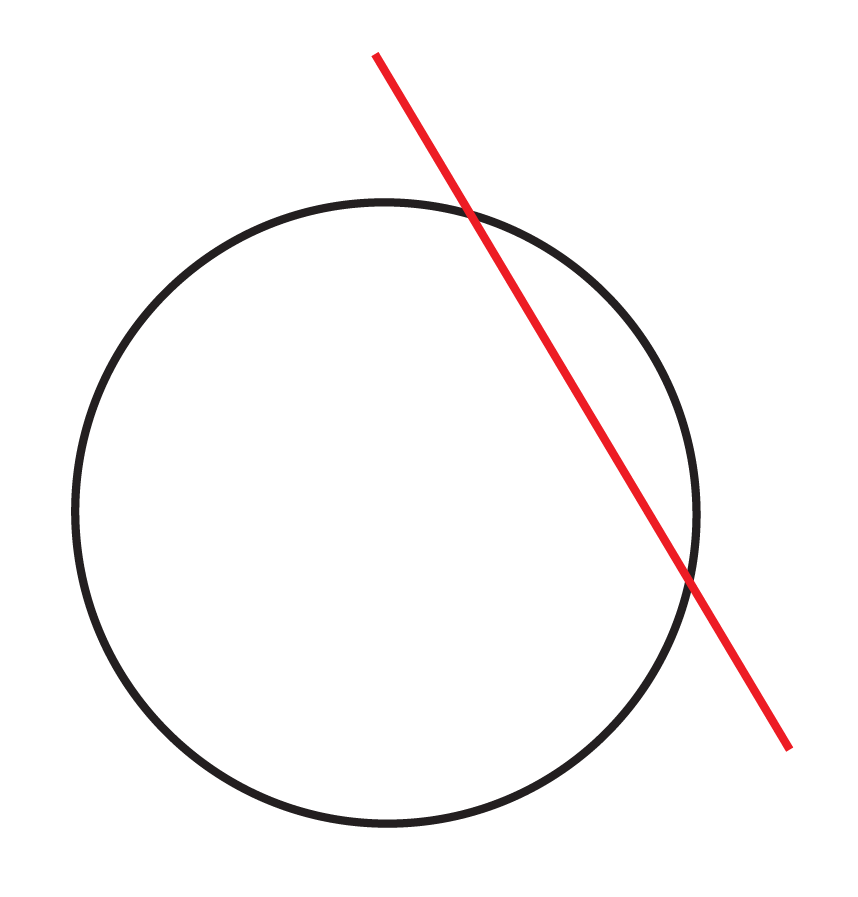
The red line is not tangential to the circle because it intersects the circumference of the circle at more than one exact point. A line that intersects a circle in exactly two points is called a secant.