
Hey, guys! Welcome to this video on finding the slope!
Reviewing the Basics
So, I’m assuming that you already know how to find the slope of a line when given the equation of a line.
We know that the standard form for the equation of a line is \(y=mx + b\), where \(m\) is our slope and \(b\) is our \(y\)-intercept.
We also know that slope is rise over run, or \(y\) over \(x\).
But now, how do we find the slope of a line when only given two points on a graph?
Let’s take a look.
Finding the Slope of a Line
Example #1
So, we have our graph.
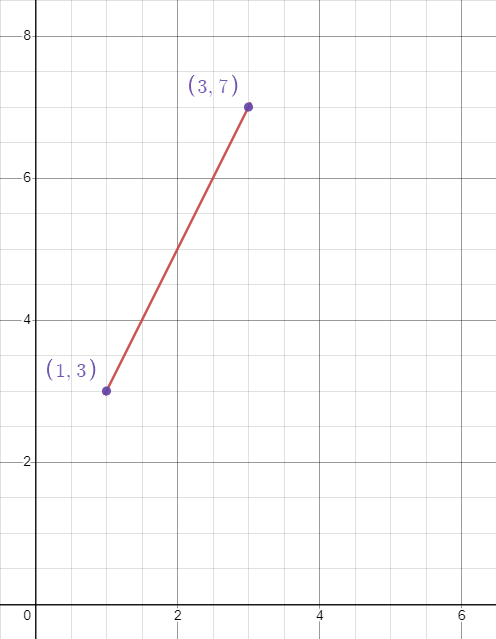
So, we have two points on our line \((1,3)\) and \((3,7)\), but how do we find the slope of the line?
Well, we can do this by dividing the difference of the \(y\)-coordinates of the two points you’ve been given by the difference of the \(x\)-coordinates from the same set of points.
Let me just write out, mathematically, everything that I just said.
So, we find the slope by dividing by the difference between our \(y\)-coordinates. That can be written like this: \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\text{slope}\)
Now, you just need to plug in your \(y\)-values and your \(x\)-values.
Example #2
But here’s another very important thing that many students get confused about, and it’s a great question: Which set of coordinates are my \(x_{1}\) and \(y_{1}\), and which set of coordinates are my \(x_{2}\) and \(y_{2}\)?
The answer is: It doesn’t matter.
However, what you can’t do is assign \(x_{1}\) to the \(x\)-value in a set of coordinates, and \(y_{2}\) to the corresponding \(y\)-values. For example, in our points on the graph above, I couldn’t say that the 1 is my \(x_{1}\) and then the 3 is my \(y_{2}\). If I make 1 \(x_{1}\), then my corresponding \(y\)-value here has to be \(y_{1}\). What doesn’t matter is whether or not I make this set of points my \((x_{1},y_{1})\), or this set of points my \((x_{1},y_{1})\).
So now, let’s pick whichever point we want to be our \((x_{1},y_{1})\) and for this video I’ll just say that \((1,3)\) will be our \((x_{1},y_{1})\), which makes \((3,7)\) our \((x_{2},y_{2})\).
Now, let’s plug in our values:
Since 7 is our \(y_{2}\), we have \(7-y_{1}\), and our \(y_{1}\) is equal to 3. So, \(7-3\). Over the difference between our \(x\)-values, \(x_{2}\), which is 3 minus \(x_{1}\), which is 1.
So we have \(\frac{7-3}{3-1}\). That’s gonna give us \(\frac{4}{2}\), which reduces to be \(\frac{2}{1}\), which is the same thing as 2.
Just to show you guys it doesn’t matter which set of points you make your \((x_{1},y_{1})\), and \((x_{2},y_{2})\), I’ll switch them around.
So let’s make \((1,3)\) \((x_{2},y_{2})\) and \((3,7)\) \((x_{1},y_{1})\).
When we plug them in we get \(\frac{3-7}{1-3}=\frac{-4}{-2}\). When we have a negative divided by a negative you get a positive, so this simply reduces to \(\frac{2}{1}\), or 2.
So, we see that our two answers are the same, and that it does not matter which set of coordinates we assign to be our \((x_{1},y_{1})\), and \((x_{2},y_{2})\).
I hope this video has been helpful to you!
See you next time!
Slope of a Line Practice Questions
In the standard equation of a line, what do the variables m and b represent in \(y=mx+b\)?
The correct answer is m represents slope and b represents the y-intercept. In the equation \(y=mx+b\), x and y represent a coordinate pair \((x, y)\) that is located on the line of the equation. The variable m represents the slope of the line, and b represents the y-intercept, or where the line crosses through the y-axis.
What is the slope of the line below?
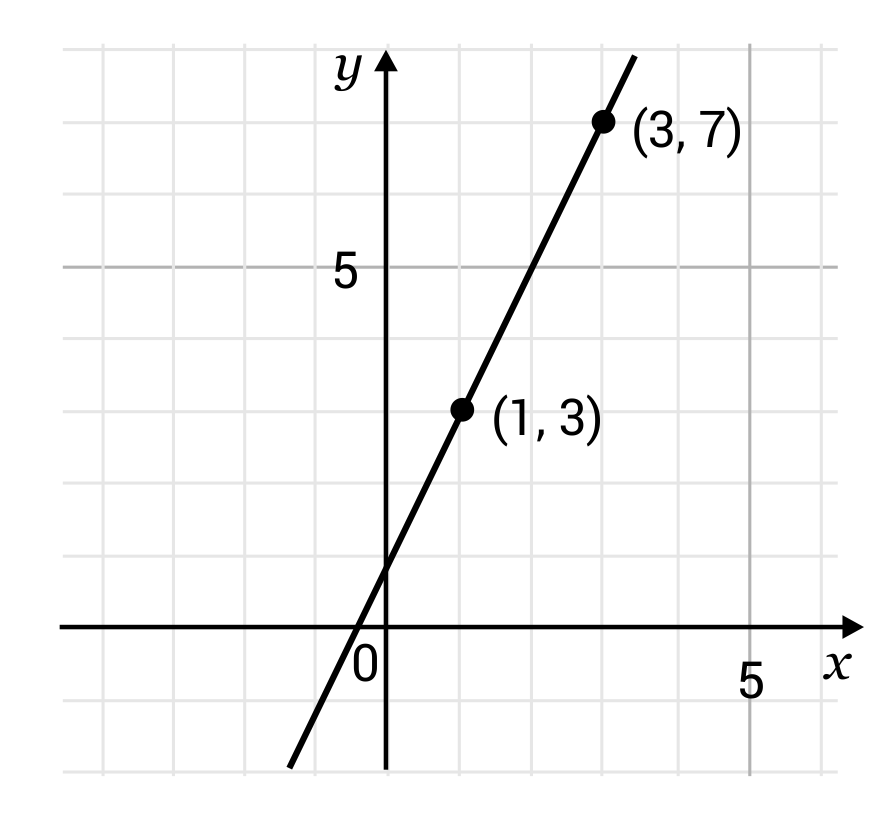
The correct answer is 2. The slope of the graphed line can be found by using the two plotted points \((1, 3)\) and \((3, 7)\). The slope can be calculated by dividing the difference of the y-coordinates by the difference of the x-coordinates. Plug in the x and y coordinates:
\(y-y\) would be \(3-7=-4\)
\(x-x\) would be \(1-3=-2\)
\(\frac{-4}{-2}=2\)
The slope of the line, therefore, is 2.
What is the slope of the line below?
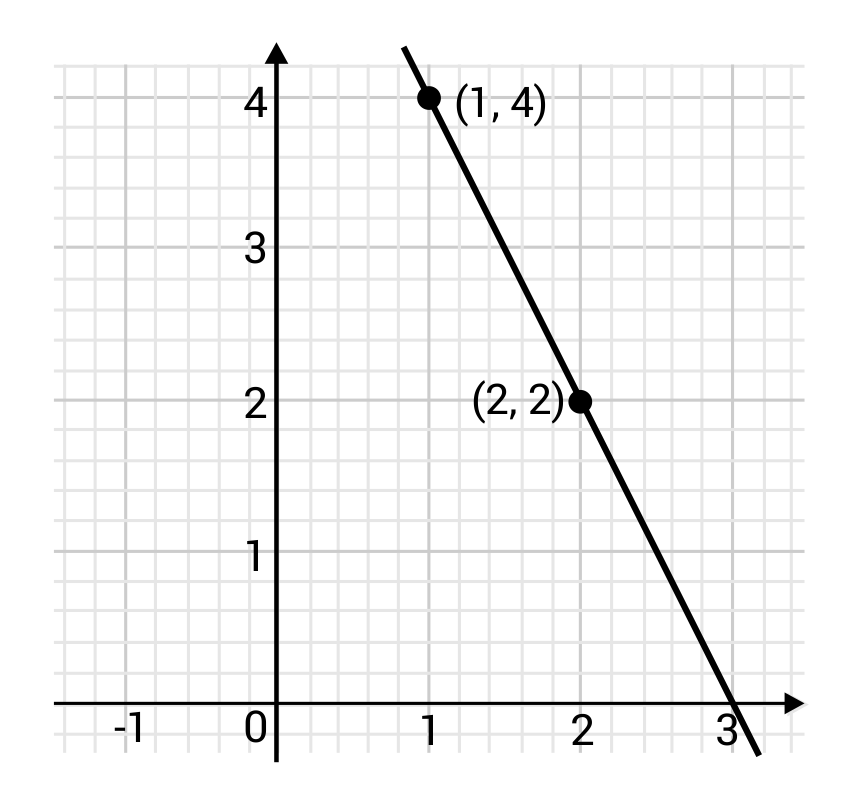
The correct answer is -2. The slope of the graphed line can be found using the two plotted points \((1, 4)\) and \((2, 2)\). Calculate the slope by dividing the difference of the y-coordinates by the difference of the x-coordinates. Plug in the x and y coordinates:
\(y-y\) would be \(4-2=2\)
\(x-x\) would be \(1-2=-1\)
\(\frac{2}{-1}=-2\)
The slope of the line, therefore, is -2.
What is the slope of the line below?
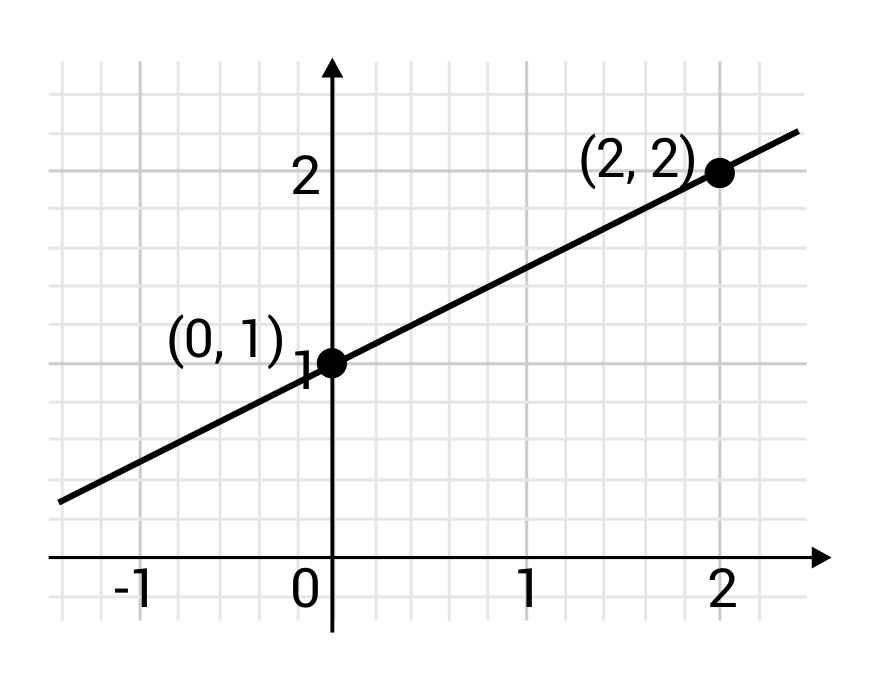
The correct answer is \(\frac{1}{2}\). The slope of the graphed line can be found using the two plotted points \((0, 1)\) and \((2, 2)\). The slope can be calculated by dividing the difference of the y-coordinates by the difference of the x-coordinates. Plug in the x and y coordinates:
\(y-y\) would be \(1-2=-1\)
\(x-x\) would be \(0-2=-2\)
\(\frac{-1}{-2}=\frac{1}{2}\)
The slope of the line, therefore, is \(\frac{1}{2}\).
What is the slope of the line below?
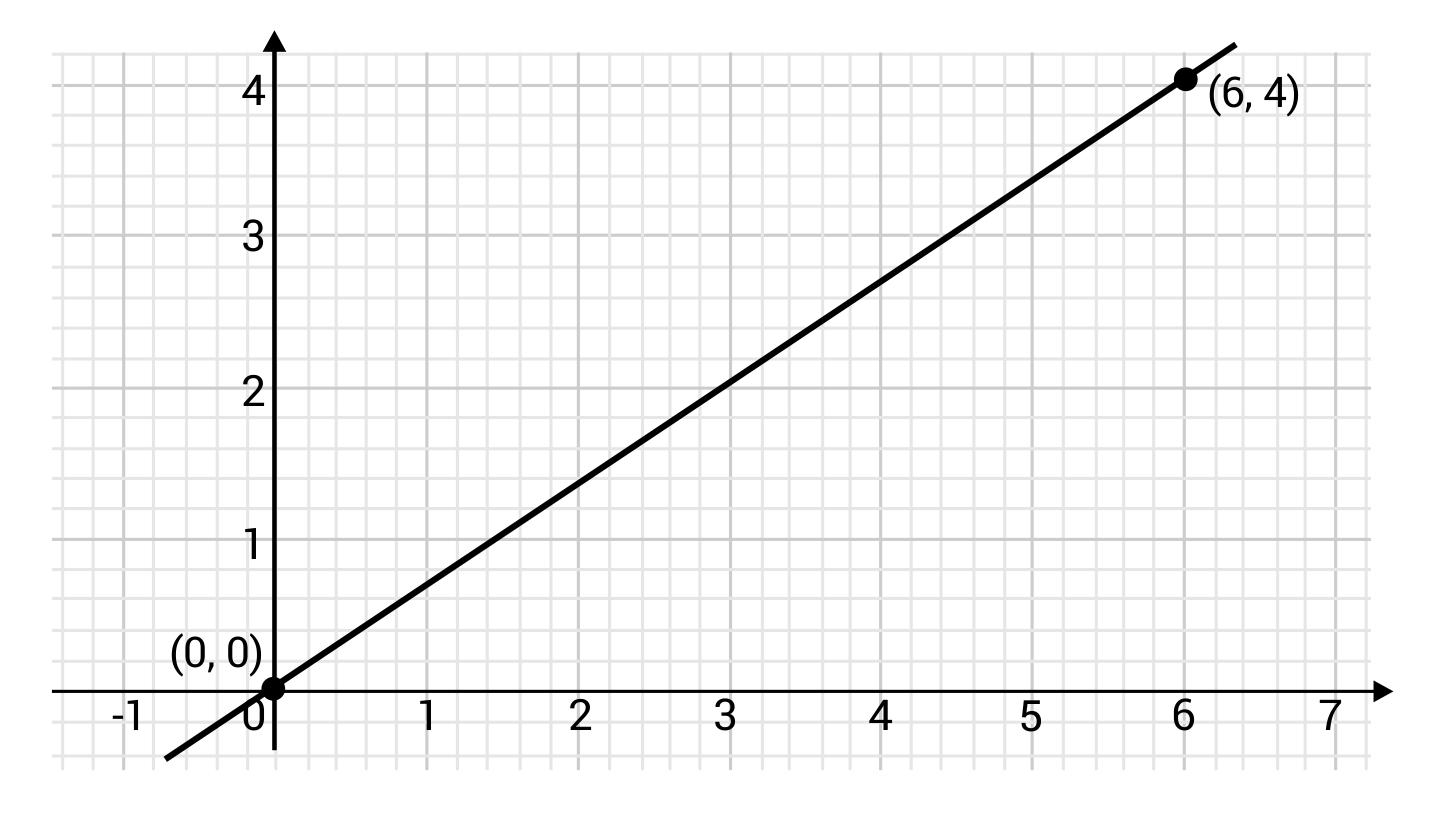
The correct answer is \(\frac{2}{3}\). The slope of the graphed line can be found using the two plotted points \((0,0)\) and \((6,4)\). The slope can be calculated by dividing the difference of the y-coordinates by the difference of the x-coordinates. Plug in the x and y coordinates:
\(y-y\) would be \(0-4=-4\)
\(x-x\) would be \(0-6=-6\)
\(\frac{-4}{-6}=\frac{4}{6}=\frac{2}{3}\)
The slope of the line, therefore, is \(\frac{2}{3}\).
