
Hi, and welcome to this review of linear equation forms! Specifically, we’ll be talking about slope-intercept and point-slope forms. We will also review the terminology and the process of graphing linear equations in these forms. Let’s get started!
A linear equation can be expressed in many different ways, but no matter which form you use, it just represents a straight line.
Standard Form
The standard form of a linear equation is written as: \(Ax +By=C\), where \(A\), \(B\), and \(C\) are constants, and \(x\) and \(y\) represent variables. This form of the equation is very useful for some purposes in math.
For example, a line can be quickly graphed when it is in this form by finding the \(x\)– and \(y\)-intercepts. There are also methods of solving systems of equations that require each equation in the system to be written in this form.
Slope-Intercept Form
Rearranging the standard form equation into slope-intercept form, \(y=mx + b\), reveals other key features of the line, namely, the slope and the \(y\)-intercept. The slope of a line describes the slant, or steepness, and the \(y\)-intercept is the point on the graph where the line crosses the \(y\)-axis.
Notationally, slope is represented by \(m\) and the \(y\)-intercept is represented by \(b\). Because the \(y\)-intercept is an actual point on the coordinate plane, it is represented as an ordered pair, \((0,b)\).
Converting Between Forms
Sometimes you will be asked to rearrange an equation from one form to another. Here’s an example:
Remember, the standard form of a linear equation is \(Ax +By=C\), so this is currently in standard form. If we want to change it to slope-intercept form, we are going to need to rearrange it so that \(y\) is by itself our the left side.
Our first step is to subtract \(2x\) from both sides.
\(3y=12-2x\) is what we have now.
Then, we’re going to divide everything by 3, which gives us \(y=4- \frac{2}{3}x\).
This is almost right, but if we look again at slope-intercept form we see that we need the \(x\)-term to be in front. Thankfully we can think of this as \(4+(- \frac{2}{3}x)\) and use the commutative property of addition to swap their places. This gives us:
\(y=-\frac{2}{3}x+4\)
The resulting equation is more informative about the line than the original equation in standard form. The coefficient of \(x\), \(-\frac{2}{3}\), is the slope. A negative slope tells us that the line slants downward, from left to right. The \(y\)-intercept of 4 tells us that the line crosses the \(y\)-axis at the point \((0,4)\).
Slope Example Problems
Now that we have seen how to convert a standard form equation into slope-intercept form, let’s practice recognizing the key features of slope and the \(y\)-intercept with a few examples.
For these examples, we want to name the slope, describe the slant of the line, and name the \(y\)-intercept as an ordered pair.
Example #1
The slope of this equation is \(m=2\), the coefficient of the \(x\)-variable. A positive slope indicates that the line slants upward from left to right. The \(y\)-intercept is \(b=3\), which indicates that the line crosses the \(y\)-axis at the point, \((0,3)\).
Example #2
Let’s try another one:
The slope of this equation is \(m=\frac{3}{5}\). Because the slope is positive, the line slants upward from left to right. The \(y\)-intercept is \(b=-\frac{2}{3}\), which indicates that the line crosses the \(y\)-axis at the point, \((0,-\frac{2}{3})\).
Example #3
Let’s try one more:
The slope is \(m=-5\). Negative slope means that the line slants downward from left to right; the line crosses the \(y\)-axis at the point \((0,-2)\).
Graphing from the Y-Intercept
As you can imagine, knowing where the line crosses the \(y\)-axis and the slope of the line will make the line very easy to graph. Now, let’s take a look at how slope provides you with instructions to graph from the \(y\)-intercept.
Any value of slope can be looked at as a fraction, where the numerator indicates where to move along the \(y\)-axis, and the denominator indicates where to move along the \(x\)-axis.
Movement along the \(y\)-axis is typically referred to as the “rise.” A positive rise value would instruct a move up the \(y\)-axis, while a negative rise would indicate a move down the \(y\)-axis. Likewise, a positive run value would mean a shift to the right, and a negative run would mean a shift to the left.
Rise and Run Examples
Here are a few examples to practice identifying the rise and run indicated by a given slope:
Example #1
This slope is not written as a fraction, but any whole number can be rewritten as a fraction over 1:
The numerator, 5, is the rise. Positive value means UP, 5. The denominator is the run. Positive value means RIGHT, 1.
Example #2
Let’s try another one.
When you have a negative slope, you can consider either the numerator or the denominator to be negative, not both! For this example, let’s consider the numerator, the rise, to be the negative value.
Negative value means DOWN, 2. The denominator, 3, is the run. Positive value means RIGHT, 3.
Example #3
Here’s one last example:
First, we need to rewrite the whole number as a fraction: \(m=-\frac{3}{1}\). Let the numerator be the negative value. Rise is -3, DOWN, 3. Run is 1, RIGHT, 1.
Graphing Examples
Now onto some graphing. People sometimes find it helpful to use the notation of slope-intercept form to get started. “Begin” at \(b\), and “Move” according to \(m\).
Example #1
Let’s graph the linear equation in slope-intercept form:
Step 1: Begin at \(b\)
Plot the \(y\)-intercept, \((0,-2)\), 1st point.
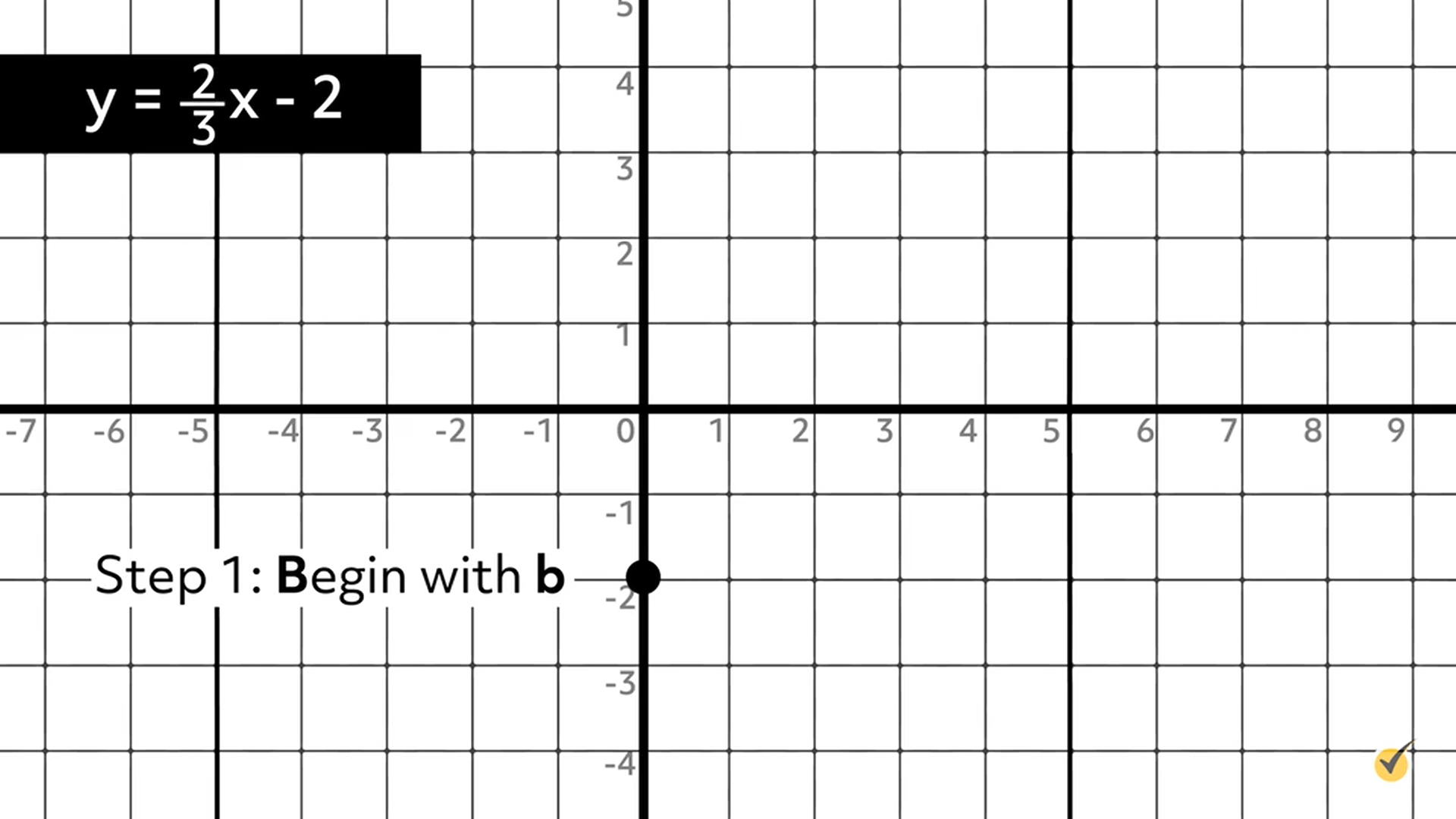
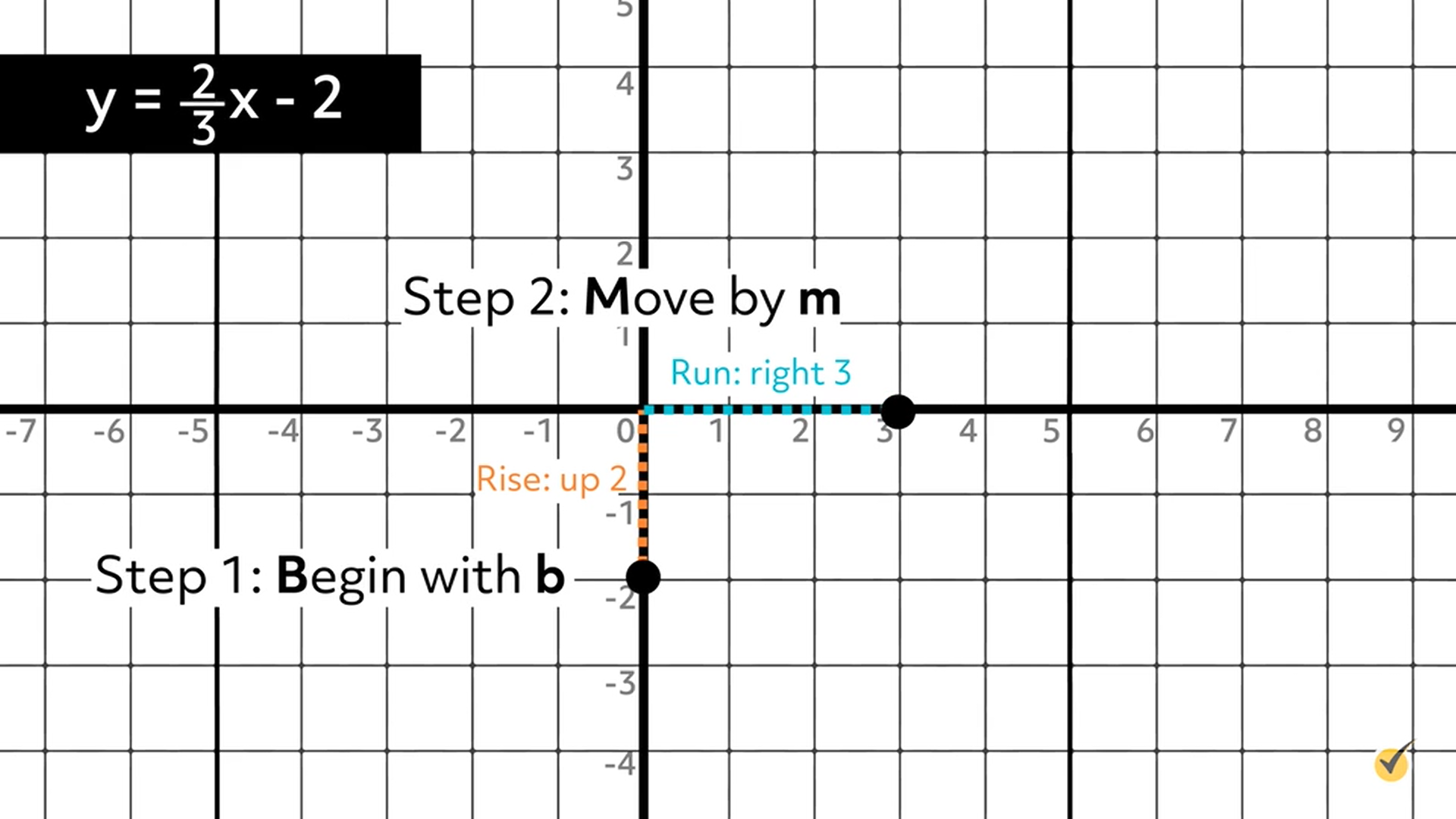
Step 2: Move by \(m=\frac{2}{3}\)
Rise equals UP, 2.
Run equals RIGHT, 3.
Plot the 2nd point at \((3,0)\).
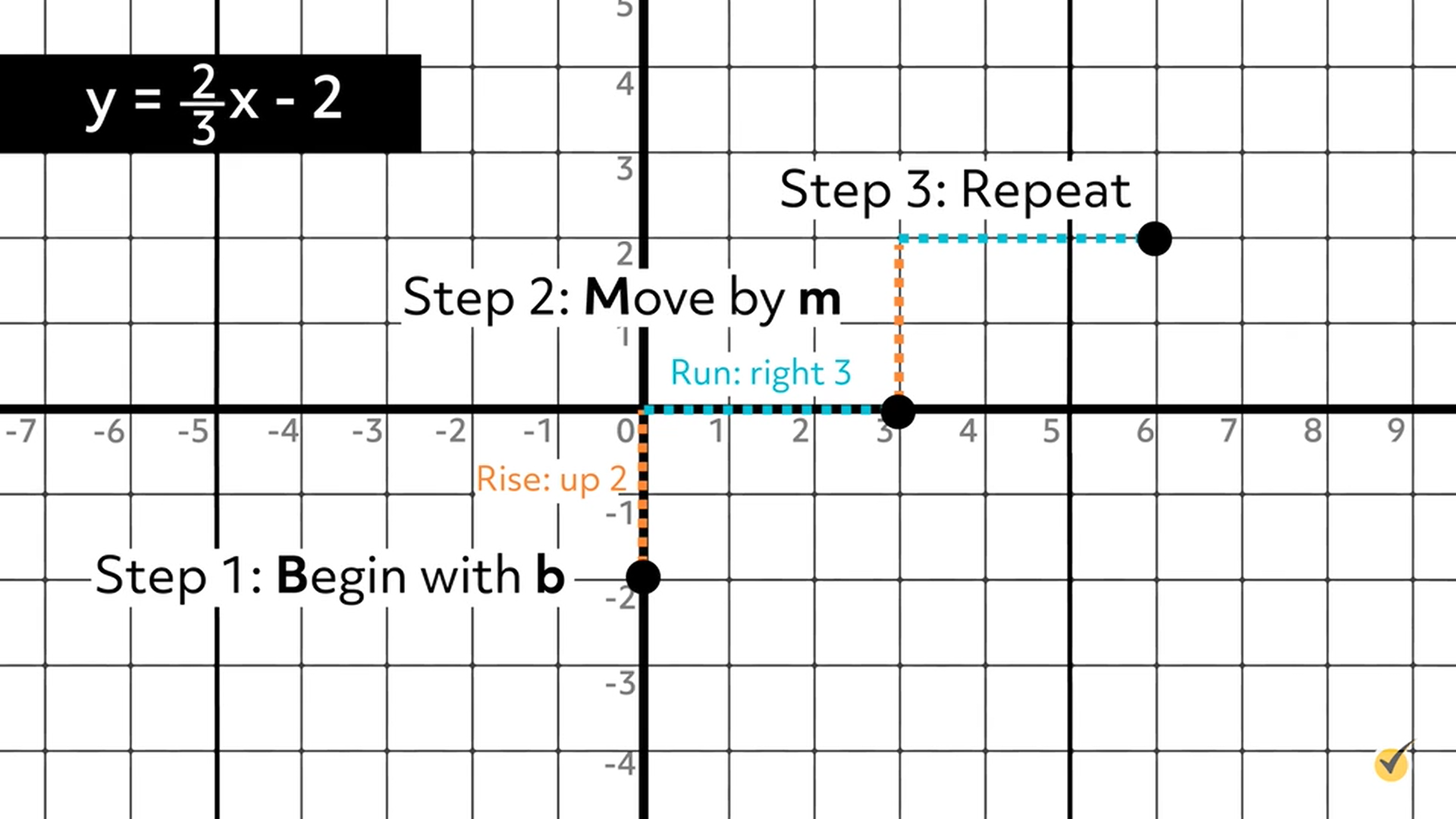
Step 3: Repeat.
Rise equals UP, 2
Run equals RIGHT, 3
Plot the 3rd point at \((6,2)\).
Step 4: Draw a straight line through the three points.
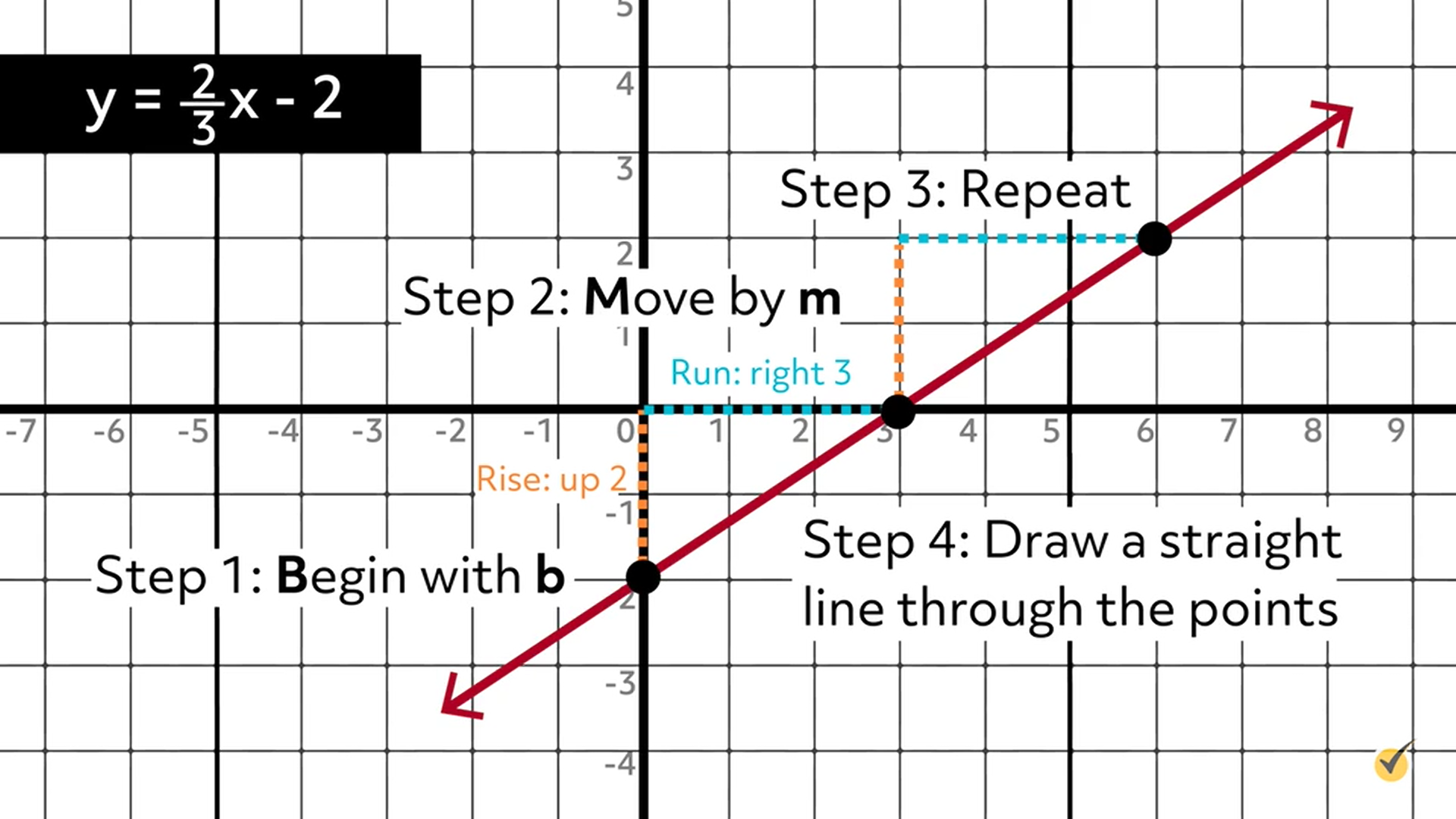
Got the hang of it? Let’s try one more:
Example #2
Step 1: Begin at \(b\),
Plot the \(y\)-intercept, \((0,-3)\), 1st point.
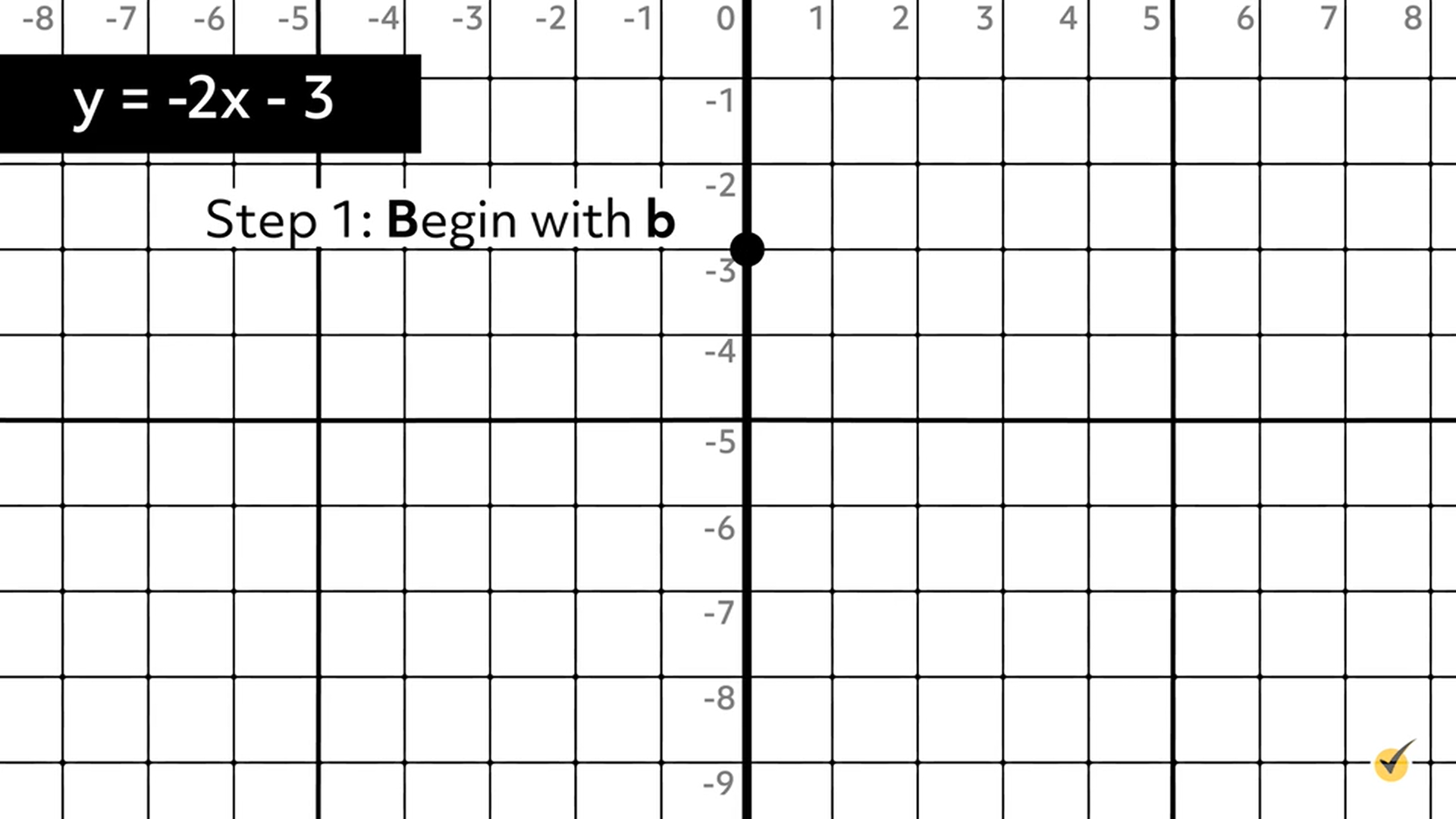
Step 2: Move by \(m=-\frac{2}{1}\). (Let the rise be negative!)
Rise equals DOWN, 2
Run equals RIGHT, 1
Plot the 2nd point at \((1, -5)\).
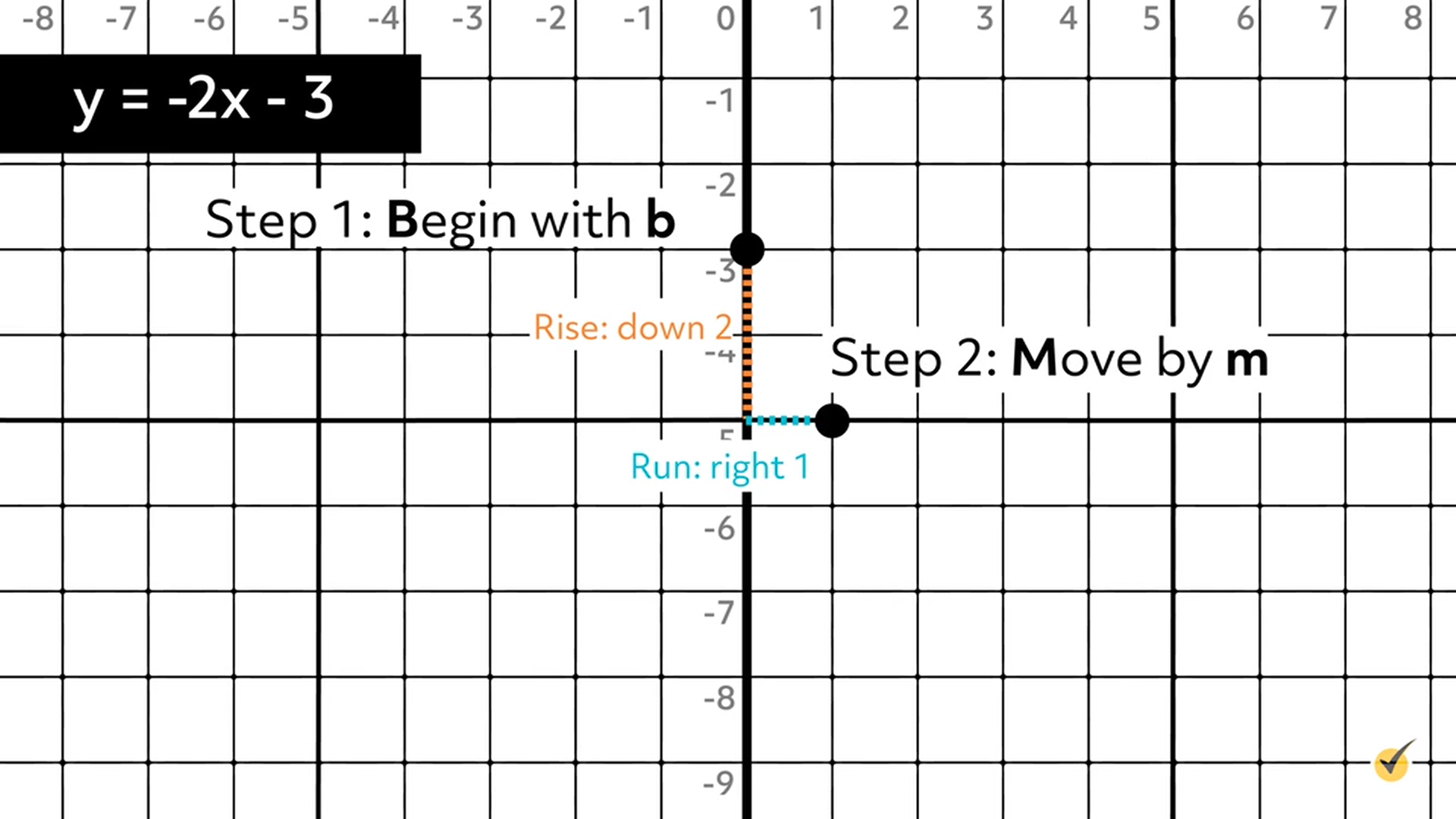
Step 3: Repeat.
Rise equals DOWN, 2
Run equals RIGHT, 1
Plot the 3rd point at \((2, -7)\).
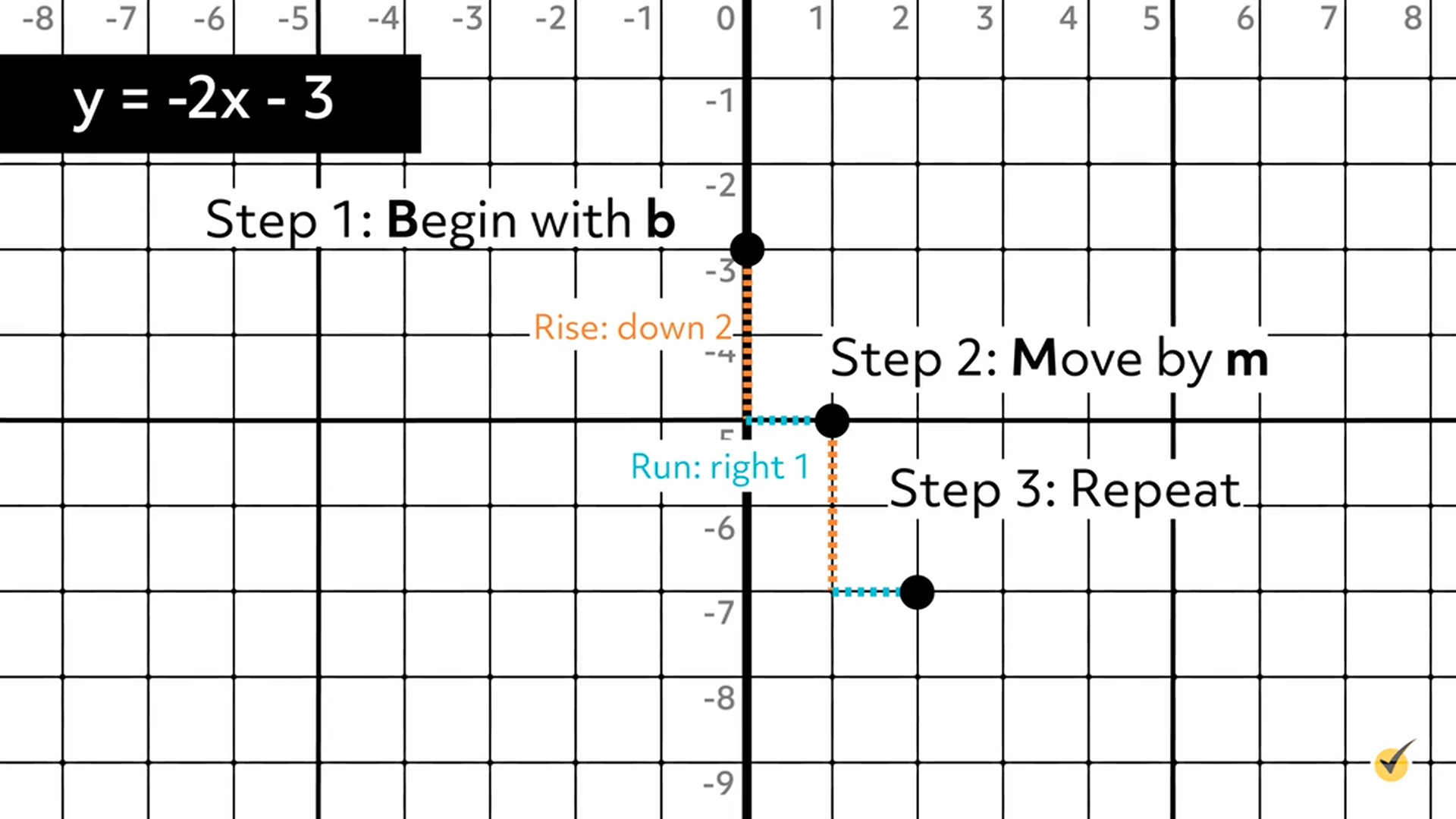
Step 4: Draw a straight line through the three points.
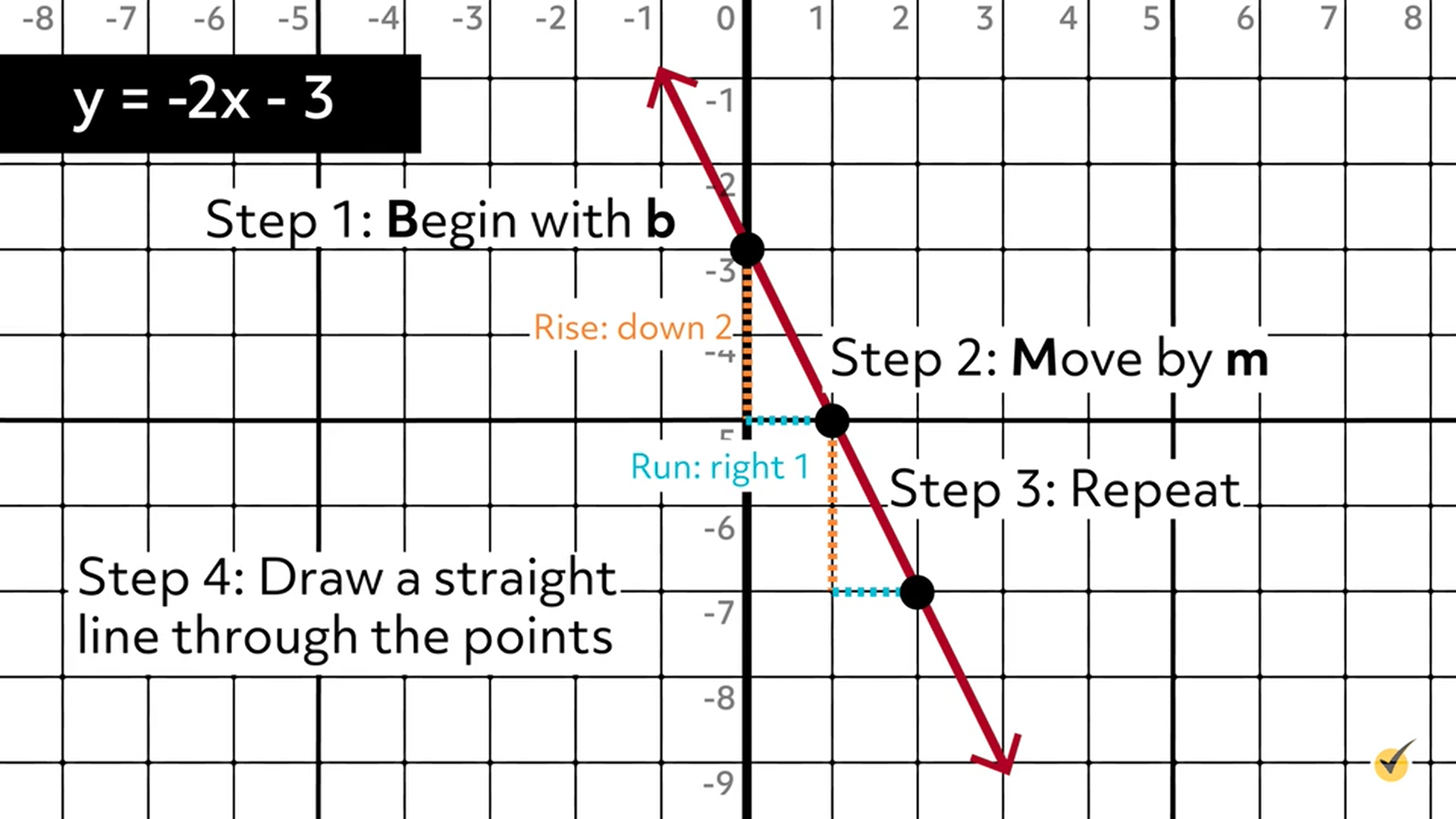
Note the slant downward, from left to right, due to the negative slope in this equation.
Point-Slope Form
Now that we have had some review of the key features of linear equations, we have the tools to explore the point-slope form. This form is of special use if we know one point that is on the line, and the slope. The general form of this arrangement is \(y-y_{1}=m(x-x_{1})\), where \(m=\text{slope}\) and \((x_{1},y_{1})\) is another point that is known on the line.
Using this template, let’s practice identifying the slope and the point from the following examples of point-slope form:
Example #1
This is a straightforward example. First, identify the slope as the coefficient outside the parentheses, \(m=3\). When naming the point on the line, note that in the general form the \(x\)-coordinate is being subtracted from \(x\), and the \(y\)-coordinate is being subtracted from \(y\), so the ordered pair of the point will be \((2,5)\).
Example #2
Here’s another one:
The slope in this equation is \(m=-\frac{1}{2}\).
How is this equation different from the general form \(y-y_{1}=m(x-x_{1})\)? You may have noticed that the \(y\)-value of the point, 3, is being added.
To identify the point that is on this line, the equation must look like the general form, which subtracts the coordinates of the point. Therefore, the point can be seen more clearly if the equation is written as:
(Subtracting a negative value is the same as addition.)
Now, we can see that this line travels through the point, \((4,-3)\) and has a slope of \(m=-\frac{1}{2}\).
Example #3
Let’s look at one more example:
By now, you can quickly see that the slope of this equation is \(m=-3\). This equation also does not “match” the general form but it can be rewritten as follows: \(y-(-12)=-3(x-(-5))\). This adjustment reveals that the point that is on the line, \((-5,-12)\).
Once you feel comfortable with identifying the slope and the point from this form, you can graph the line as we did before.
Step 1: Identify the slope, \(m=\frac{1}{2}\).
Step 2: Identify the point on the line, \((2,5)\).
Some students find it helpful to “switch the sign” of the given formula to determine the coordinates of the point!
Step 3: Plot the point, \((2,5)\), as the first point.
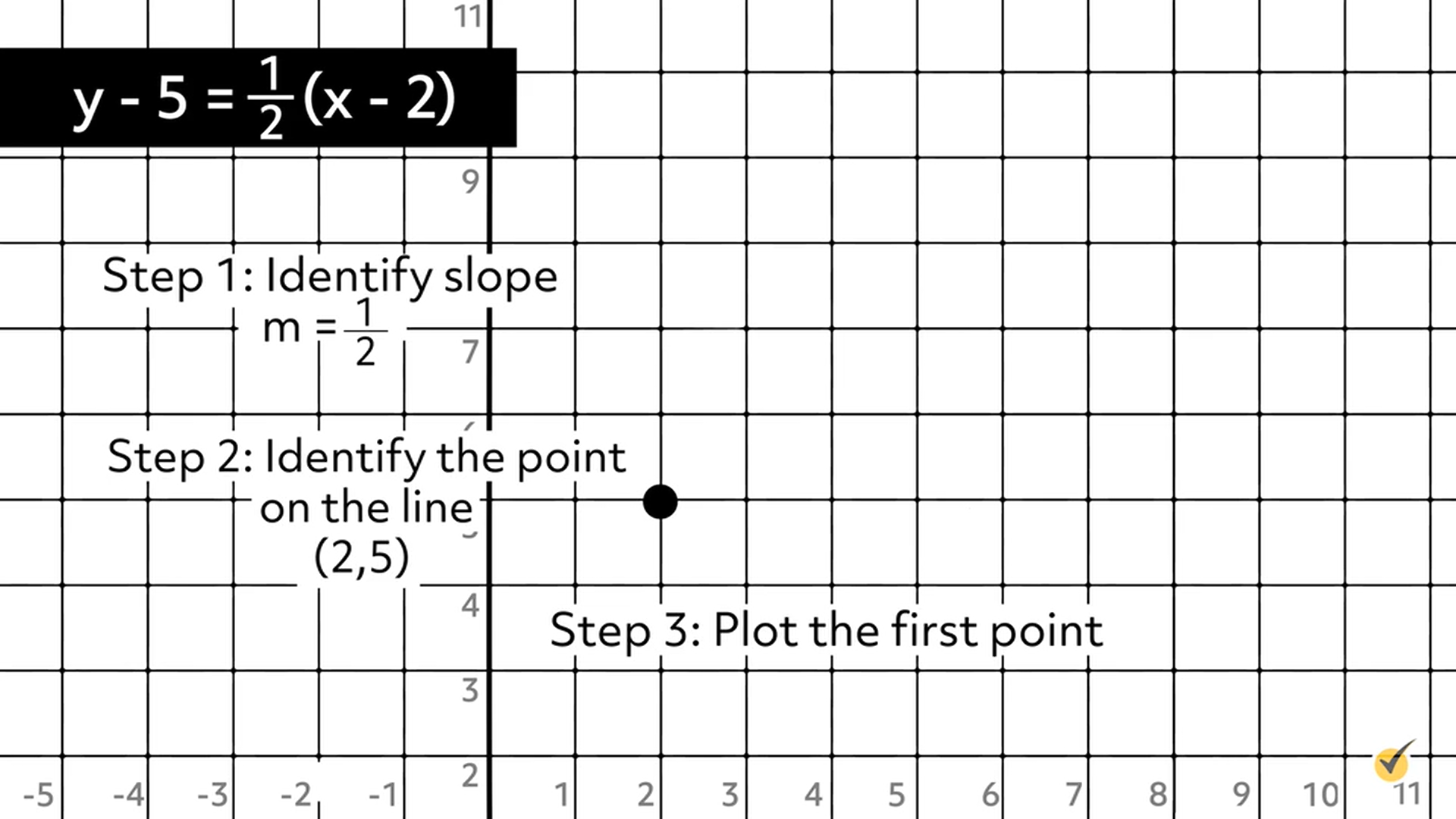
Step 4: Move by \(m=\frac{1}{2}\).
Rise equals UP, 1
Run equals RIGHT, 2
Plot the 2nd point at \((4,6)\).
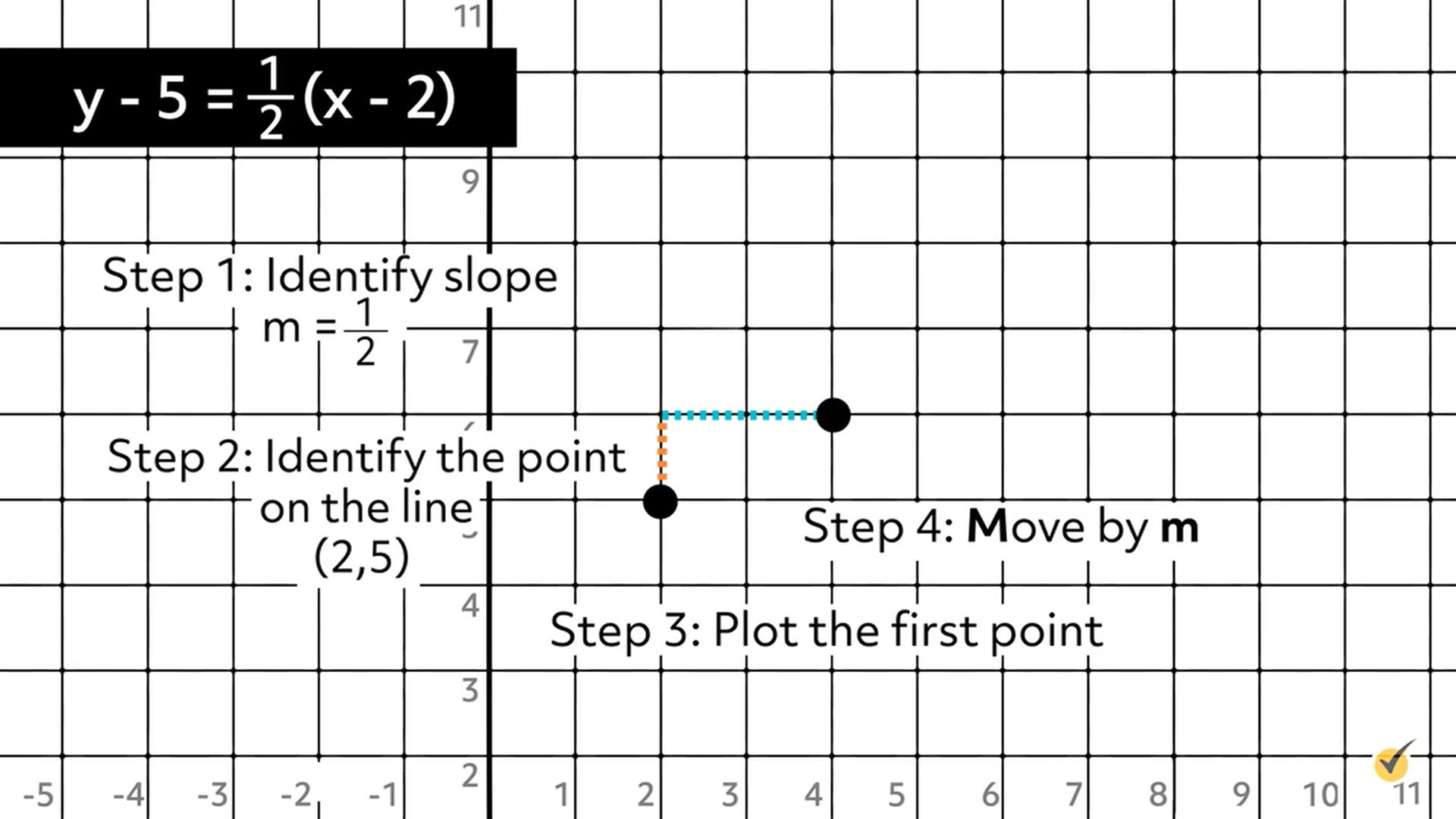
Step 5: Repeat.
Rise equals UP, 1
Run equals RIGHT, 2
Plot the 3rd point at \((6,7)\).
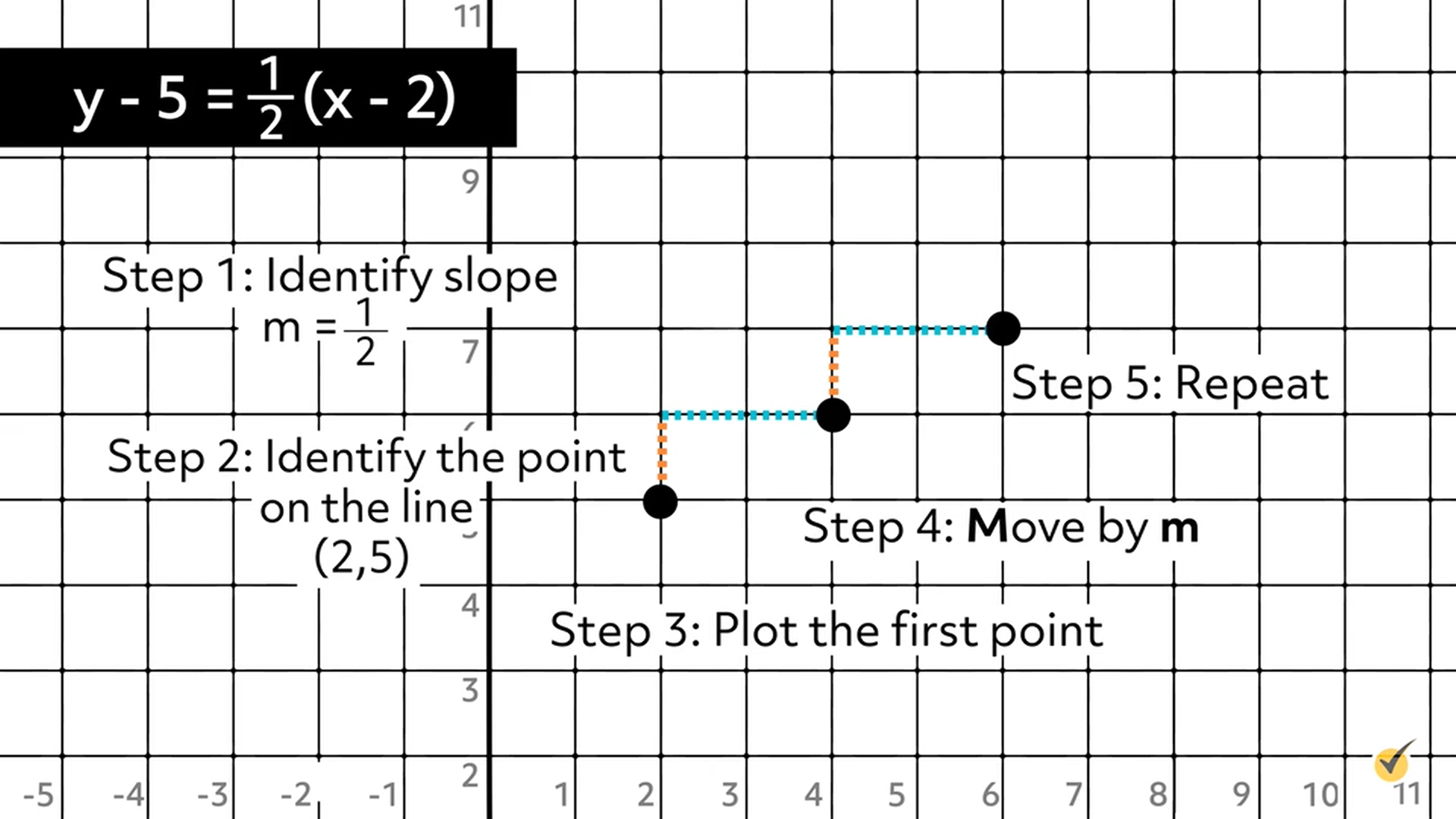
Step 6: Draw a straight line through the three points.
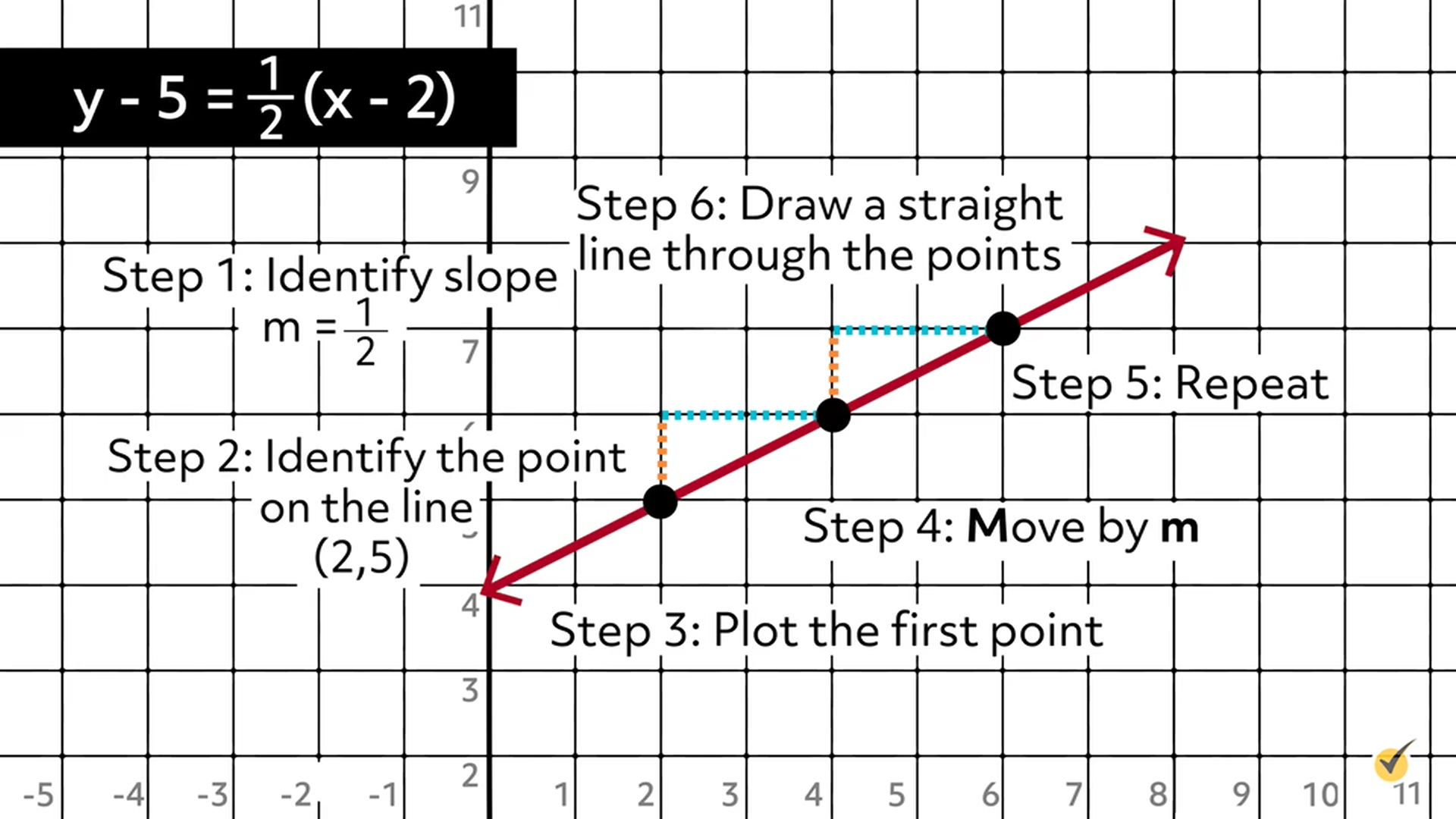
Alright, we’ve covered a lot of ground in this video regarding the different ways linear equations can be written. While the structure of the equations looks different, they all represent a line. The use of each depends on what you are given or what you are asked to do.
That’s all for this review! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is slope-intercept form?
A
Slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
Q
How do you graph slope-intercept form?
A
Graph slope-intercept form by first plotting the y-intercept, then using the slope to find a second point and plotting that point, and finally drawing a line through the two points.
Ex. Graph y = 2x – 3
Plot the y-intercept: (0, -3)
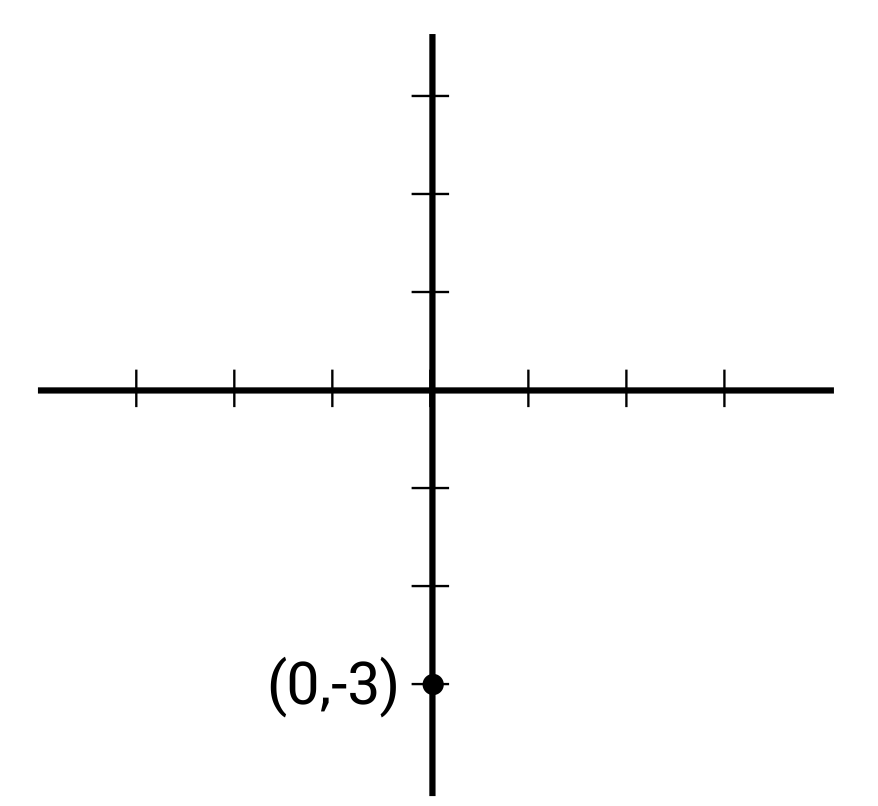
Find a second point using the slope and plot: (1, -1)
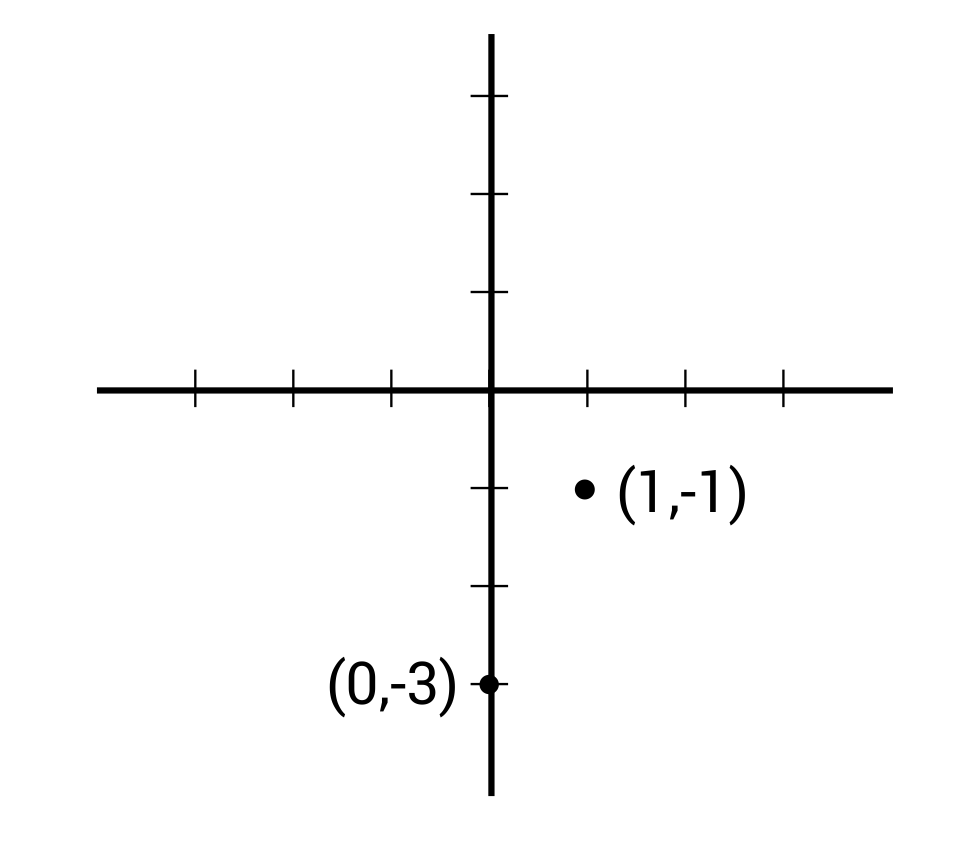
Draw a line through the 2 points
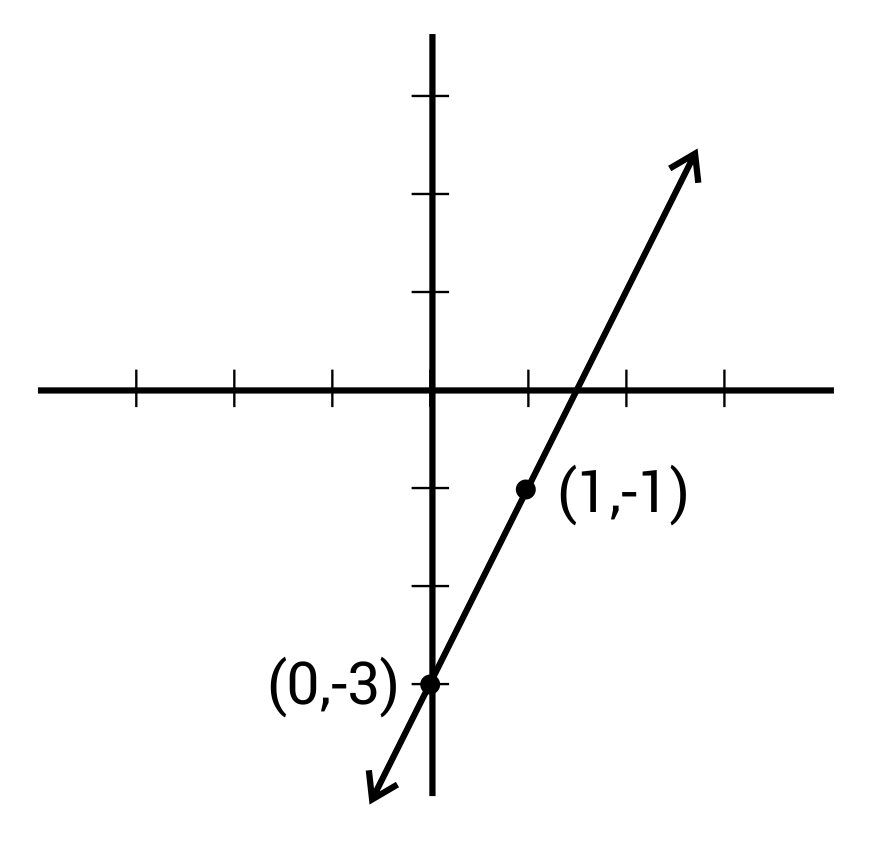
Q
What is b in slope-intercept form?
A
In slope-intercept form, b stands for the y-intercept of the line.
Q
What is point-slope form?
A
Point-slope form is a linear equation in the form:
\(y-y_1=m(x-x_1)\)
Q
How do you graph point-slope form?
A
To graph point-slope form (y – y1 = m(x – x1)), first plot the point (x1,y1). Then, use the slope (m) to find a second point on the line. Plot that point. Finally, draw a straight line through the two points.
Ex. Graph y – 7 = -4(x – 1)
First, plot the point (x1,y1), which in this case is (1, 7).
Then, use the slope to find a second point. The slope is -4, so move right 1 and down 4. The new point is (2, 3). Plot this point.
Finally, draw a line through these two points.
Slope-Intercept and Point-Slope Practice Questions
Which of the following equations is in slope-intercept form?
The correct answer is \(y=4x-3\). Equations in slope-intercept are in the form \(y=mx+b\), where m is the slope and b is the y-intercept.
Which of the following equations is in point-slope form?
The correct answer is \(y-11=2(x+14)\). Equations in point-slope form have the form \(y-y_1=m(x-x_1)\), where \((x_1,y_1)\) is a point on the line and m is the slope of the line.
Which of the following equations is in standard form?
The correct answer is \(19x+3y=27\). Equations in standard form have the form \(Ax+By=C\).
What is the equation \(3x+4y=12\) in slope-intercept form?
The correct answer is \(y=-\frac{3}{4}x+3\). Equations in slope-intercept form have the form \(y=mx+b\). To get \(3x+4y=12\) in that form, manipulate the equation to isolate y.
\(3x+4y=12\)
Subtract 3x from both sides.
\(4y=12-3x\)
Divide both sides by 4.
\(y=3-\frac{3}{4}x\)
Rearrange the right side so it is in the proper form.
\(y=-\frac{3}{4}x+3\)
What is the point-slope equation \(y-7=13(x+3)\) in slope-intercept form?
The correct answer is \(y=13x+46\). Equations in slope-intercept form have the form \(y=mx+b\). To get \(y-7=13(x+3)\) in that form, manipulate the equation to isolate y.
\(y-7=13(x+3)\)
Distribute 13 to \((x+3)\).
\(y-7=13x+39\)
Add 7 to both sides.
\(y=13x+46\)



