
Hello, and welcome to this video on linear equations! In this video we will look at:
- What linear equations are, and
- How to solve for different variables in a linear equation
What exactly is a linear equation? Well, if you look at the word linear you can find the word line, so a linear equation is an equation for a line. Linear equations have two variables, most commonly \(x\) and \(y\), that are to a single degree, meaning they do not have variables to powers or roots. The equation \(y = 9x + 5\) is an example of a linear equation.
Determining Linear Equations
Let’s look at some equations and determine if they are linear. As each equation is shown, I want you to decide if it is linear or not.
Example #1
No, this is not a linear equation because the \(x\)-variable is squared.
Example #2
Yes, this is a linear equation. There are two variables and they are both of a single degree.
Example #3
Yes, even though this equation looks a little different from our other ones, it is still a linear equation because there are two variables and neither one has a root or is raised to a power.
Example #4
No, this is not a linear equation because of the square root.
Slope-Intercept Form
The most common way you will see linear equations is in the form “\(y=\)” because this is the easiest way to create a graph based on the equation. This is called slope-intercept form. However, it is still okay to have an equation with the \(x\)-variable, or both the \(x\)– and the \(y\)-variables, on the left side of the equation.
Example #1
Let’s look at an equation that has the \(x\)-variable on the left side and rearrange it so it is in slope-intercept form.
When we are looking for slope-intercept form, we want to get the \(y\)-variable by itself on the left side of the equation. To do this, we first have to add 7 to both sides.
Then we divide by 2 to get \(y\) by itself.
Remember, dividing by 2 is the same as multiplying by \(\frac{1}{2}\), so another way to write this equation is:
All that’s left is to flip our equation around so the \(y\) is on the left side of the equation.
Now we have our equation in slope-intercept form!
Example #2
Let’s look at one more equation, but this time we are going to solve for \(x\).
Our first step to get our \(x\)-variable by itself on the left side is to subtract \(6y\) from both sides of the equation.
Then, we divide the whole equation, which means both parts of the right-hand side of the equation, by -3.
This is technically correct, but the best way to write an equation like this is to have the variable before the number so we are going to rearrange it to look like this.
Remember, the other way wasn’t incorrect, but this is the more proper way to write our equation.
I hope this overview of linear equations was helpful! Thanks for watching and happy studying!
Frequently Asked Questions
Q
How do you solve linear equations?
A
Solve linear equations by using the Order of Operations in reverse and use opposite operations on both sides of the equation to undo the operations until the variable is isolated. The order of operations is: parentheses, exponents, multiplication and division from left to right, addition and subtraction from left to right. To isolate a variable, work through this process backwards, starting with addition and subtraction and ending with parentheses.
Ex. 2(4x + 10) = -12
Divide by 2 on both sides.
4x + 10 = -6
Subtract 10 from both sides.
4x = -16
Divide by 4 on both sides.
x = -4
Q
How do you graph linear equations?
A
Graphing linear equations is typically done by plotting a point given in the equation, plotting a second point by using the slope, and drawing a straight line through the two points. Each form of an equation will have a different point to start with. Slope is rise over run, so to find your second point, move up (or down if there is a negative) the amount in the numerator and right the number in the denominator.
Ex. Point-Slope: (y – 3) = 4(x – 7)
Plot the first point from the equation: (7,3)
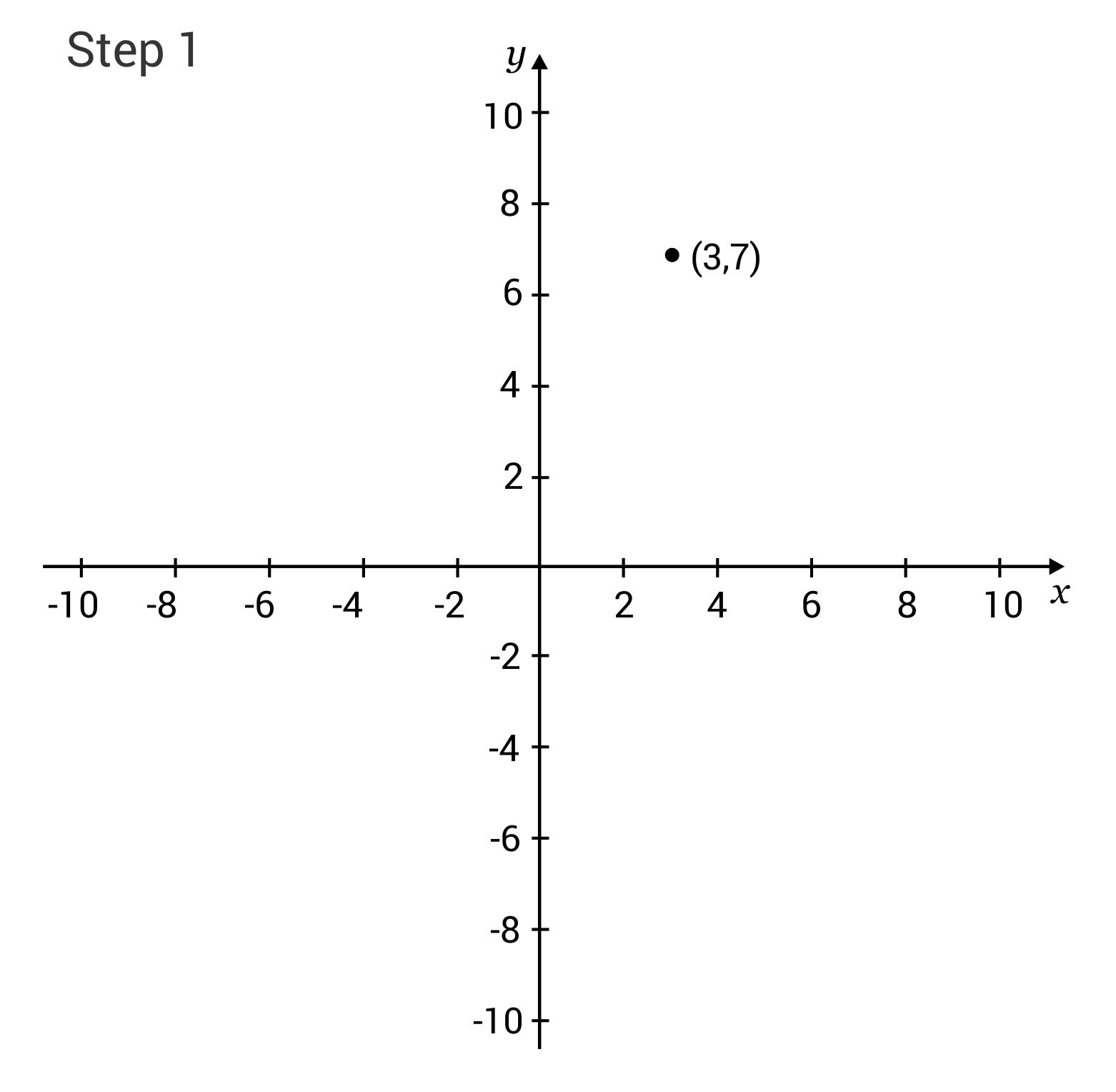
Plot the second point, found by using the slope: (4, 11) – The slope is 4, or 4/1, so move up 4 and right 1.
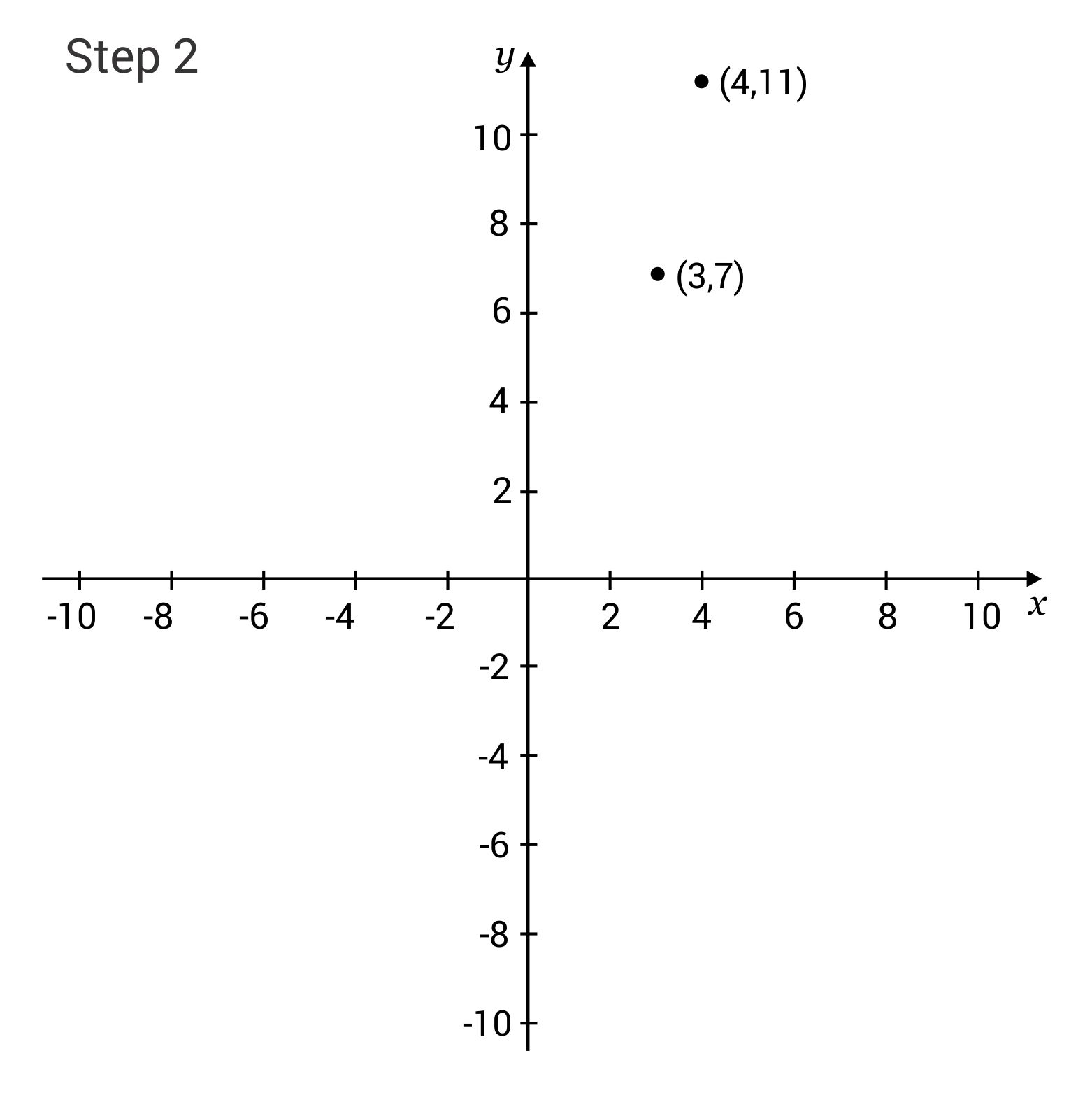
Draw a line through the two points
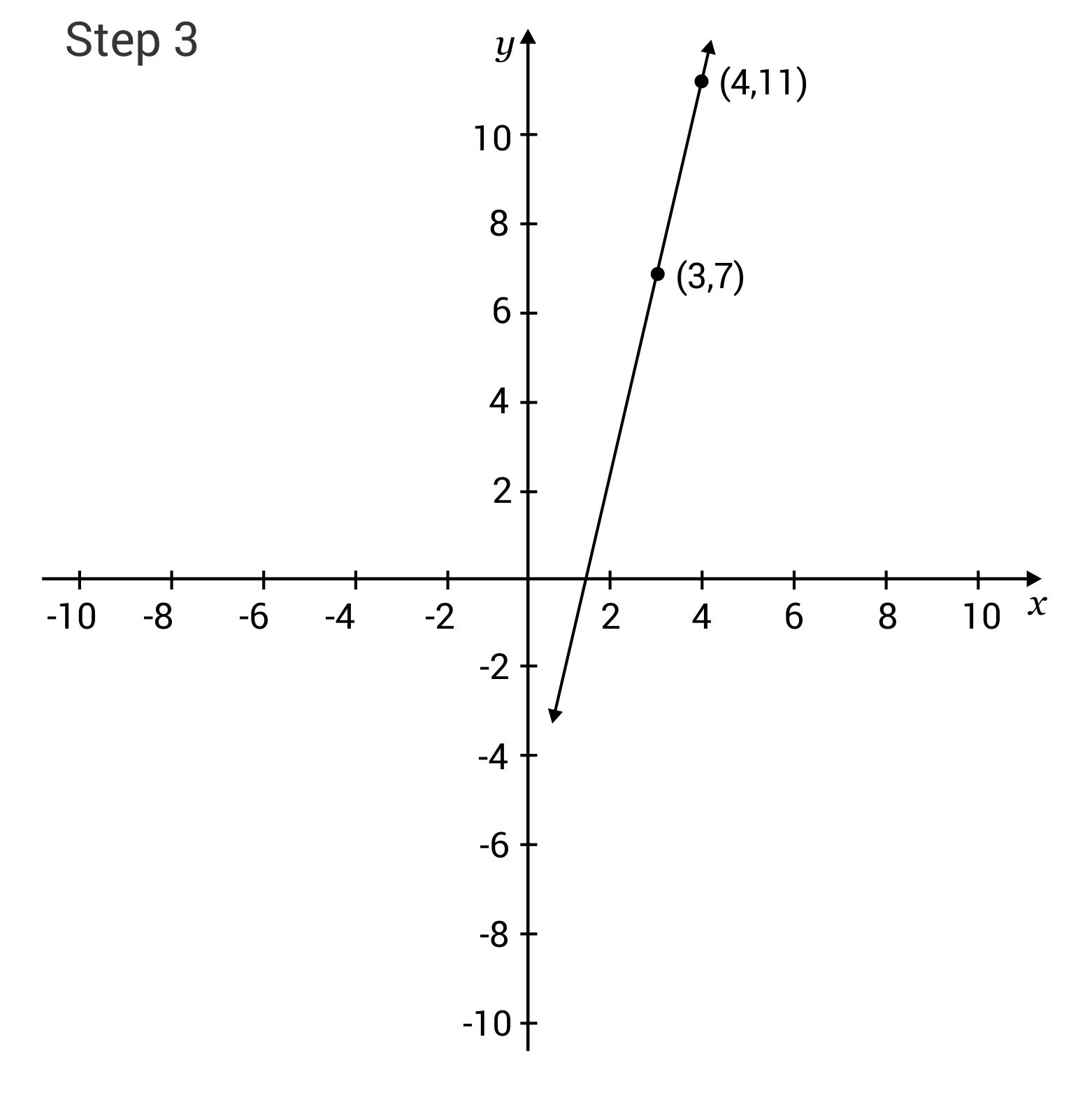
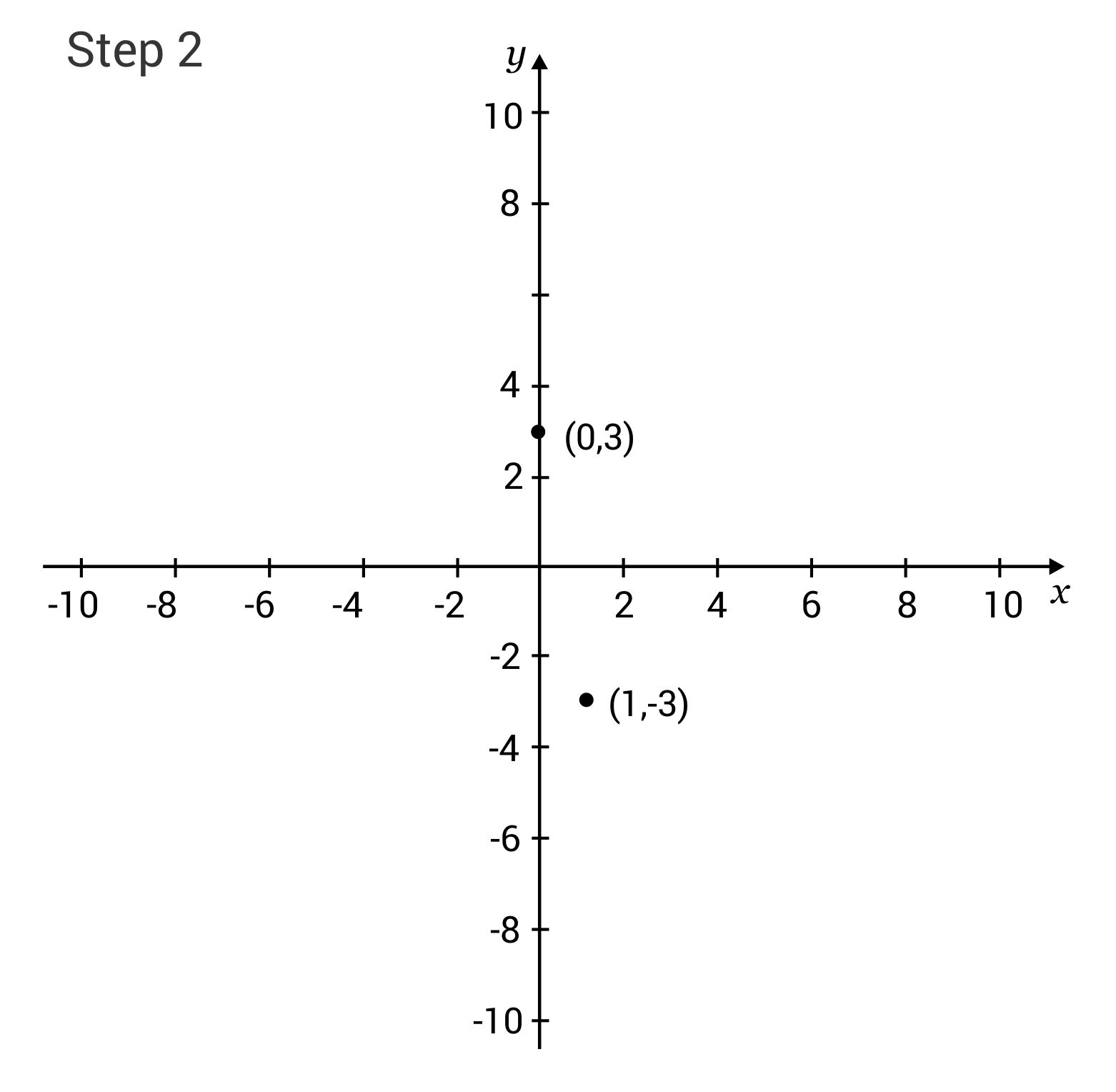
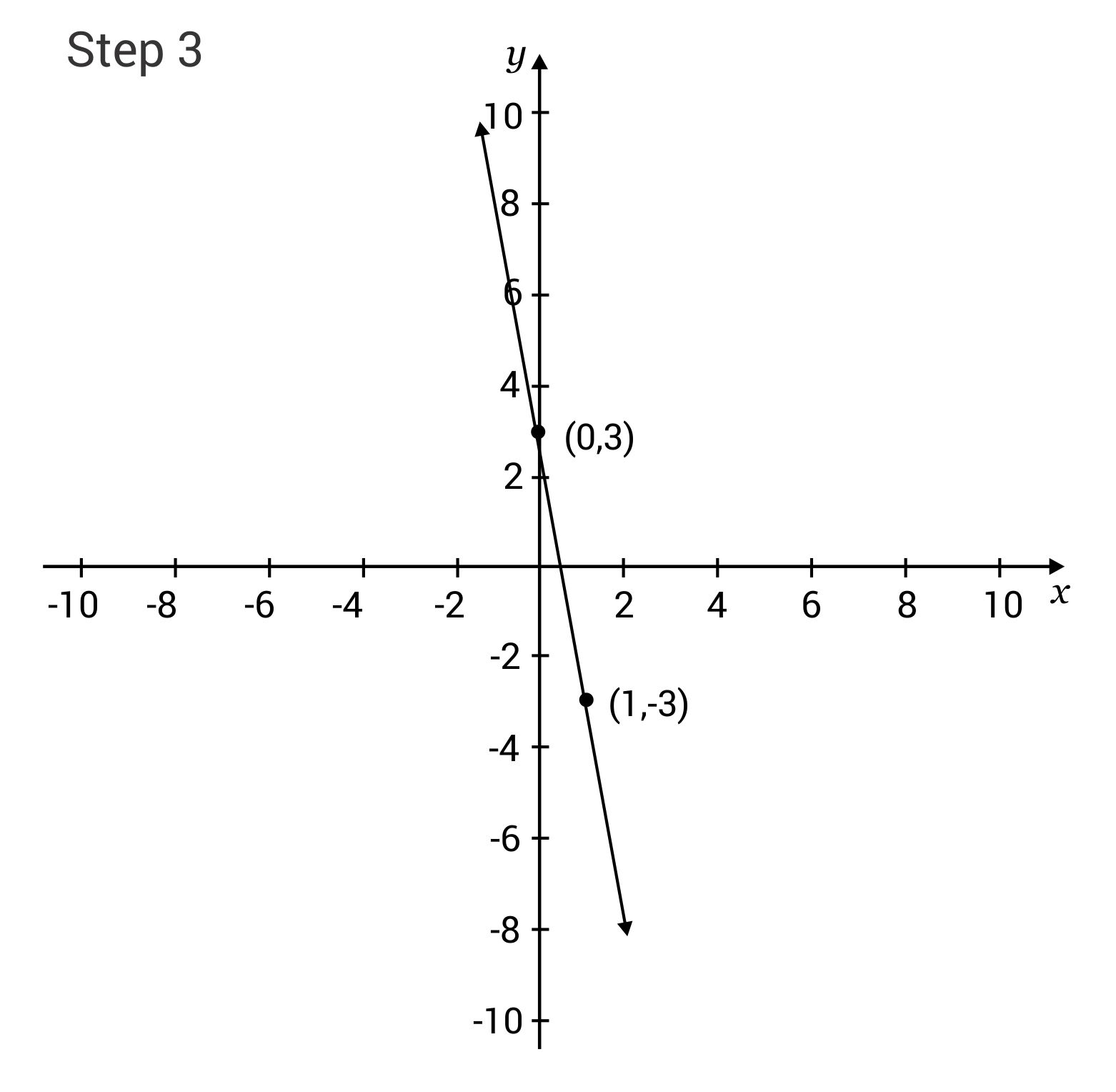
Slope-Intercept: y = -6x + 3 Plot the first point from the equation (y-intercept): (0, 3)
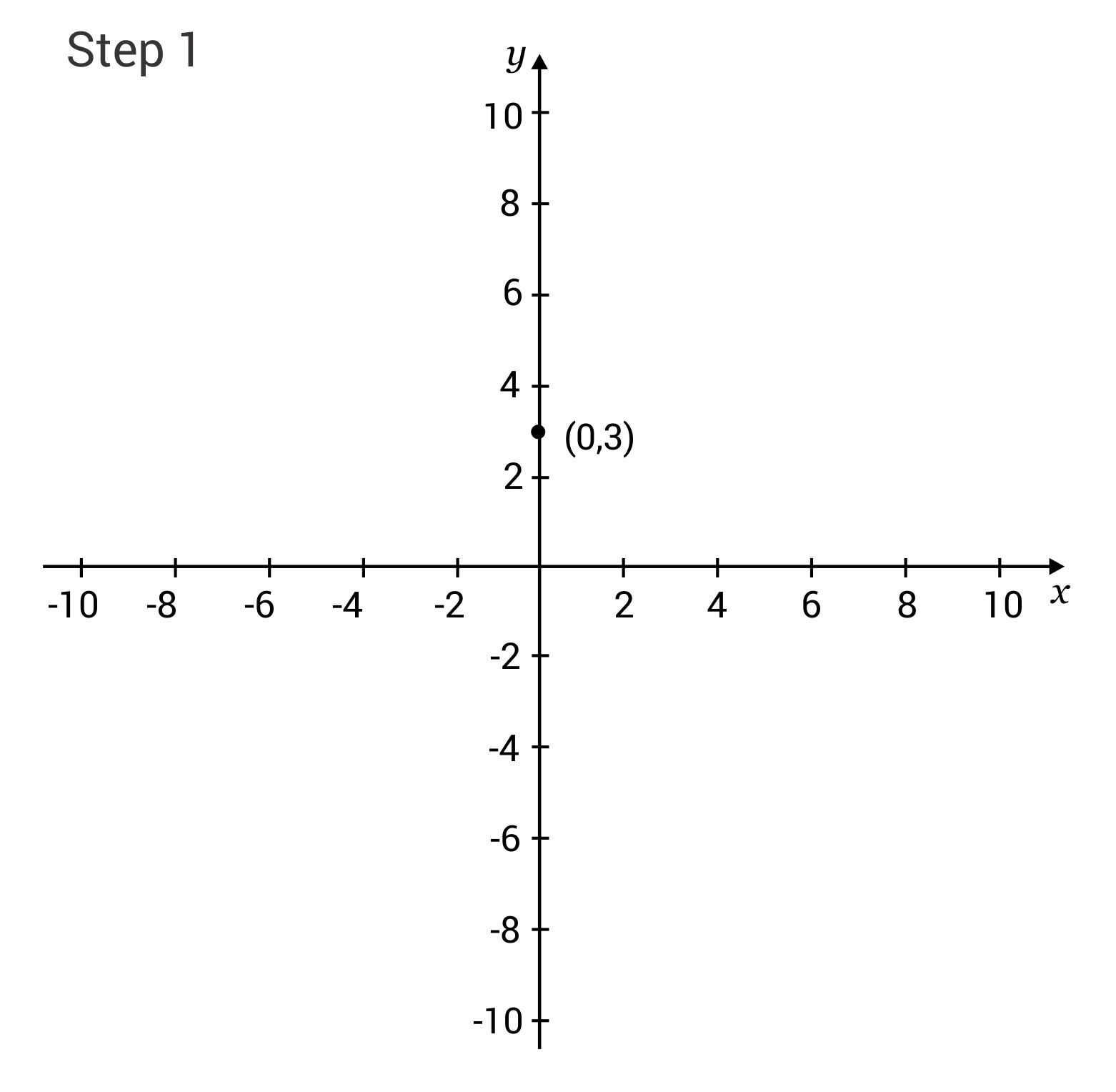
Plot the second point, found by using the slope: (1, -3) – The slope is -6, or -6/1, so move down 6 and right 1.
Draw a line through the two points
Q
How do you solve linear equations with fractions?
A
Solve linear equations with a fraction multiplied by the variable by multiplying both sides by the reciprocal of the fraction. This makes the number in front of the variable a 1, so the fraction goes away.
Ex. Solve for x: \(\frac{2}{3}x-7=29\)
First, add 7 to both sides.
\(\frac{2}{3}x=36\)
Then, multiply by the reciprocal of the fraction (\(\frac{3}{2}\)).
\((\frac{3}{2})(\frac{2}{3})x=36(\frac{3}{2})\)
\(x=54\)
Linear Equation Practice Questions
What is \(-3x+2y=12\) in slope-intercept form?
The slope-intercept form is when the equation looks like \(y=mx+b\), where the slope and y-intercept are visible in the equation. To change the equation from standard form to slope-intercept form, we solve the equation for y.
\(-3x+2y=12\)
\(2y=3x+12\)
\(\frac{2y}{2}=\frac{3x}{2}+\frac{12}{2}\)
\(y=\frac{3}{2}x+6\)
Which is a linear equation?
Since the definition of a linear equation is an equation of a line where the x-term and y-term are raised to a single degree, the equation \(y=\frac{1}{2}x+5\), is the only equation that meets this requirement. Therefore, it is a linear equation.
Which shows \(x=-\frac{1}{3}y-3\) in slope-intercept form?
The slope-intercept form of an equation is the equation in terms of y. We will solve the equation until y is isolated on one side.
\(x=-\frac{1}{3}y-3\)
\(x+3=-\frac{1}{3}y\)
\(-3(x+3=-\frac{1}{3}y)\)
\(-3x-9=y\)
\(y=-3x-9\)
What is \(5x–4y=20\) in terms of x?
To put an equation in terms of x means we solve the equation to have x isolated on one side. To do that we will use our algebra skills.
\(5x–4y=20\)
\(5x=4y+20\)
\(\frac{5x}{5}=\frac{4y}{5}+\frac{20}{5}\)
\(x=\frac{4}{5}y+4\)
What is \(y=\frac{1}{3}x-5\) in terms of x?
Writing an equation in terms of x means we need to isolate the variable x on one side of the equation.
\(y=\frac{1}{3}x-5\)
\(y+5=\frac{1}{3}x\)
\(3(y+5=\frac{1}{3}x)\)
\(3y+15=x\)
\(x=3y+15\)
