
Spheres are amazing. They are perfectly symmetrical. They’re super strong because they have no weak points. They naturally occur in the form of tiny things like atoms, small things like water droplets and bubbles, and enormous things like our sun.
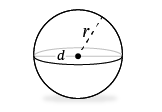
And we can calculate the volume and the surface area of all of these objects by using relatively simple formulas. All we need to know is the radius of the sphere, which is the distance from the center of the sphere to any point on the surface of the sphere.
Volume of a Sphere
Let’s tackle volume first. The volume of a sphere is the measure of how much space it takes up. We measure this in cubic units, such as cubic inches or cubic centimeters. We can picture these units as cubes that we could place inside the sphere to see how many we can fit. But since the sphere is curved, even millimeter-sized cubes wouldn’t give an exact volume. It’s like trying to make a sphere out of toy building blocks—it never really looks like a real sphere no matter how small the blocks are.
But fortunately, we have a formula to calculate the exact volume of a sphere:
Where \(r\) is the radius of the sphere. The formula isn’t exactly new. The Greek philosopher Archimedes discovered it over 2,000 years ago. But it still works as well now as it did then. Probably even better since we have electronic calculators these days.
Finding the Volume
So let’s find the volume of a common object—a billiards ball used to play pool.
An eight-ball is 5.7 centimeters in diameter. Remember that the radius of a circle is half the diameter, so all we have to do is divide 5.7 by 2 to find our radius, 2.85 centimeters. Now we can plug that into our formula:
\(V=\frac{4}{3}\pi (2.85\text{ cm})^{3}\)
Substituting using parentheses is always a good idea to keep our order of operations clear.
\(V=30.865\pi \text{ cm}^{3}\)
Leaving our answer in terms of \(\pi \) keeps our volume exact. When we multiply by \(\pi \), we’re getting an approximate value, though a very, very close approximation:
So our answer is a bit less than 100 cubic centimeters. Imagine trying to build an eight-ball-sized sphere out of 100 centimeter cubes.
Not great! But it’s 6 centimeters high and about the same volume. It seems we should be glad we don’t have to build using small cubes to find the volume of spheres!
Finding the Surface Area
We can also find the surface area of our eight ball. Unlike with prisms and solids, our sphere doesn’t have any faces. Or maybe it has an infinite number of faces. Either way, we can’t find the surface area by adding up the face area. Instead, we find the area of its entire surface area all at once using the surface area formula for a sphere:
Where, again, \(r\) is equal to our radius. Remember that the formula for the area of a two dimensional circle is \(A=\pi r^{2}\). The surface area of a sphere is simply 4 times that. We could try cutting out 4 billiard-ball-sized circles on centimeter graph paper and trying to paste them on a billiard ball, but we can probably imagine how well that would go!
Let’s use our formula instead. The radius of our eight ball is 2.85 centimeters. So just like with volume, we simply plug that into our formula:
\(SA=4\pi (2.85 \text{ cm})^{2}\)
Substituting using parentheses is always a good idea to keep our order of operations clear.
\(SA=32.49\pi \text{ cm}^{2}\)
Once again leaving our answer in terms of \(\pi \) keeps our answer exact. Then we can find our very close approximation value by multiplying by \(\pi \) on our calculator.
Our answer is a little bit more than 100 square centimeters. Remember that surface area is a measure of two-dimensional area so our units need to be square units just like the squares on our graph paper.
So how can we use these formulas to find the volume and surface area of everyday objects? The key is finding the radius, but finding it directly is a little bit difficult because we would need to be able to measure from the center of the sphere. And the center of most spheres is difficult to locate and access! Fortunately, we can easily find the diameter of a spherical object like a ball, and then we can find the radius by calculating half the diameter. Then we can use our two formulas. And that’s all there is to it!
I hope this video on finding the volume and surface area of spheres was helpful. Thanks for watching and happy studying!
For more help, check out our volume of a sphere calculator!
Volume and Surface Area of a Sphere Practice Questions
Find the volume of a sphere that has a radius of 10 inches. Round your answer to the nearest hundredth.
Start by identifying the radius of the sphere, which is 10 inches. Substitute this value into the formula \(V=\frac{4}{3}r^3\) to find the volume.
\(r=10\)
\(V=\frac{4}{3}πr^3\)
\(V=(\frac{4}{3})(π)(10)^3\)
Next, simplify the expression \(10^3\).
\(V=(\frac{4}{3})(π)(1{,}000)\)
From here, simplify the equation by multiplying \(\frac{4}{3}\) and \(1{,}000\).
\(V=1333.\overline{33}π\)
Finally, multiply by π. Round your answer to the nearest hundredth place.
\(V\approx 4{,}188.7902\)
\(V\approx 4{,}188.79\text{ in}^3\)
The volume of the sphere is approximately \(4{,}188.79\) cubic inches.
Find the surface area of a sphere that has a radius of 6 meters. Round your answer to the nearest hundredth.
Start by identifying the radius of the sphere, which is 6 meters. Substitute this value into the formula \(SA=4πr^2\) to find the surface area.
\(r=6\)
\(SA=4πr^2\)
\(SA=(4)(π)(6)^2\)
Next, simplify the expression \(6^2\).
\(SA=(4)(π)(36)\)
From here, simplify the equation by multiplying 4 and 36.
\(SA=144π\)
Finally, multiply by \(π\). Round your answer to the nearest hundredth place.
\(SA\approx 452.38934\)
\(SA\approx 452.39\text{ m}^2\)
The surface area of the sphere is approximately \(452.39\) square meters.
Find the volume of a sphere that has a diameter of 4 feet. Round your answer to the nearest hundredth.
Start by identifying the radius of the sphere. Since the radius of a sphere is half its diameter, divide 4 by 2 to get 2 feet. Substitute this value into the formula \(V=\frac{4}{3}πr^3\) to find the volume.
\(r=\frac{d}{2}=\frac{4}{2}=2\)
\(V=\frac{4}{3}πr^3\)
\(V=(\frac{4}{3})(π)(2)^3\)
Next, simplify the expression \(2^3\).
\(V=\frac{4}{3}(π)(8)\)
From here, simplify the equation by multiplying \(\frac{4}{3}\) and \(8\).
\(V=10.\overline{66}π\)
Finally, multiply by \(π\). Round your answer to the nearest hundredth place.
\(V\approx 33.51032\)
\(V\approx 33.51\text{ ft}^3\)
The volume of the sphere is approximately \(33.51\) cubic feet.
Joel is watching the NBA All-Star Game and wants to know the volume of a basketball. He knows that the radius of an official NBA basketball is about 4.7 inches. Based on this information, find the basketball’s volume. Round your answer to the nearest hundredth.
Start by identifying the radius of the sphere, which is 4.7 inches. Substitute this value into the formula \(V=\frac{4}{3}πr^3\) to find the volume.
\(r=4.7\)
\(V=\frac{4}{3}πr^3\)
\(V=(\frac{4}{3})(π)(4.7)^3\)
Next, simplify the expression \(4.7^3\).
\(V=(\frac{4}{3})(π)(103.823)\)
From here, simplify the equation by multiplying \(\frac{4}{3}\) and \(103.823\).
\(V=138.430\overline{66}π\)
Finally, multiply by \(π\). Round your answer to the nearest hundredth place.
\(V\approx 434.89277\)
\(V\approx 434.89\text{ in}^3\)
The volume of the basketball is approximately \(434.89\) cubic inches.
Kate is wrapping a birthday present for her niece. She needs to figure out how much wrapping paper is needed to cover the surface area of a beach ball. The beach ball has a diameter of 14 inches. Based on this information, find the surface area of the beach ball. Round your answer to the nearest hundredth.
Start by identifying the radius of the sphere. Since the radius of a sphere is half its diameter, divide 14 by 2 to get 7 inches. Substitute this value into the formula SA=4πr2 to find the surface area.
\(r=\frac{d}{2}=\frac{14}{2}=7\)
\(SA=4πr^2\)
\(SA=(4)(π)(7)^2\)
Next, simplify the expression \(7^2\).
\(SA=(4)(π)(49)\)
From here, simplify the equation by multiplying \(4\) and \(49\).
\(SA=196π\)
Finally, multiply by . Round your answer to the nearest hundredth place.
\(SA\approx 615.75216\)
\(SA\approx 615.75\text{ in}^2\)
The surface area of the sphere is approximately \(615.75\) square inches.