
Hey there! Welcome to this video on symmetry.
Let’s get started!
Symmetry and Congruence
What happens when I take these two shapes and I split them in half?


The shapes are identical in size and shape, right? I can see this more clearly by folding the images on top of each other.
So, we can see that when I have drawn a line, I have created two congruent shapes. Congruent means that the two shapes are identical. When you are able to draw a straight line through the center of a shape, and it creates two congruent shapes, then these two shapes are also symmetrical.
Symmetry comes from the Greek word symmetria, meaning “a similar agreement of parts.”
Symmetry, just like congruent shapes, means that one shape becomes exactly like the other when you move it in some way. The movement could be a turn, a flip, or a slide.
When a shape is not symmetrical, then this is referred to as asymmetrical.
Line and Point of Symmetry
Some shapes have lines of symmetry. A line of symmetry is a line that splits the shape in half, creating an identical shape. Some shapes only have one line of symmetry, some have two, and some have several!
However, to draw a line of symmetry, we must first identify the point of symmetry. This is because the point of symmetry marks the point that the lines of symmetry could pass through.
A point of symmetry is when there is a position or central point on an object or shape where the central point splits the object into two identical parts. And, every single line and angle on the other side of the central point is the same exact distance from the central point on each side.
That was a lot. Let’s take a look at what I mean.
Where both identical lines of the cross intersect, we can see that there is a point of symmetry, but let’s take a look at the definition to make sure.

So let me draw this line here, this point of symmetry.

Okay, does the point split the cross into two identical, or congruent, shapes? Well, if we imagined folding it over across this point, it would then split it in half. So, check!
Is every single line or angle of the cross the exact same distance from the point on each side?
So “are all these angles congruent and the same exact distance from this point” is our question.
Based on what we can see, it definitely appears that way. However, to be one hundred percent sure, we would need to measure every single line and angle. But, for this exercise, I have used an example where we are assuming all the lines and angles are the exact same distance, so check!
Finding Lines of Symmetry
Now, let’s practice finding lines of symmetry.
Example #1
Since we’ve already found the point of symmetry on the cross, let’s see how many lines of symmetry it has. How many times can we split the cross, and get identical parts?
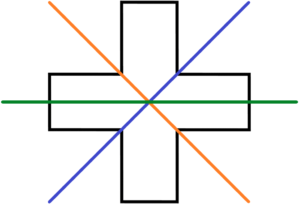
That gives us: 1, 2, 3, 4. So there are 4 lines of symmetry here, but after 4, there are no other lines that would give us two identical parts.
Great job!
Example #2
Let’s try another.
How many lines of symmetry does the dog have? Or how many lines can you draw that create multiple identical parts?

Let’s see. If we did it through the center horizontally, we wouldn’t get two identical parts because he has a lower half and then a head. So if we do it through the center from the top to the bottom, we’ll get two eyes, two parts of the nose, two halves of the mouth, two halves of the body, and two of the legs.
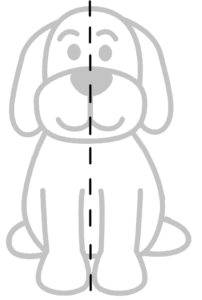
So we can see there’s one line of symmetry.
If there were any more lines, then we would not have identical parts.
Example #3
What about the side of the dog? Do you see any lines of symmetry?

No. Each end of the dog has different-shaped parts. The head is different than the tail. Let’s move on.
Example #4
Okay, now what about this thought bubble?

Is there a line you can draw to create two identical parts? No.
Example #5
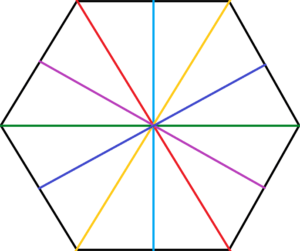
Let’s see how many lines we can draw to split this hexagon into identical parts.
1, 2, 3, 4, 5, 6.
You guys have done a really great job.
Keep practicing by looking for shapes that are symmetrical in your classroom, in your house, outside, or wherever you are.
Symmetry is everywhere, and it’s very important. Architects and engineers use symmetry to design sturdy buildings and other objects. Interior designers use symmetry and asymmetrical design to make their work more appealing to look at. People everywhere use symmetry in some way.
I hope that this video was helpful. See you next time!
Symmetry Practice Questions
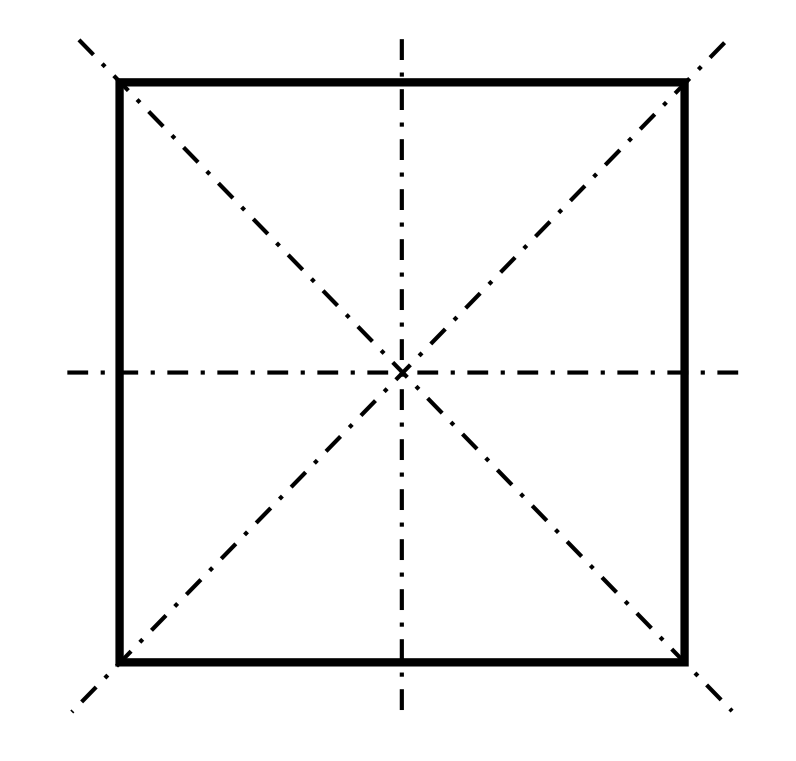
How many lines of symmetry does a square have?
A square can be folded in half horizontally, vertically, or over each diagonal shown. Therefore, the square has four lines of symmetry.
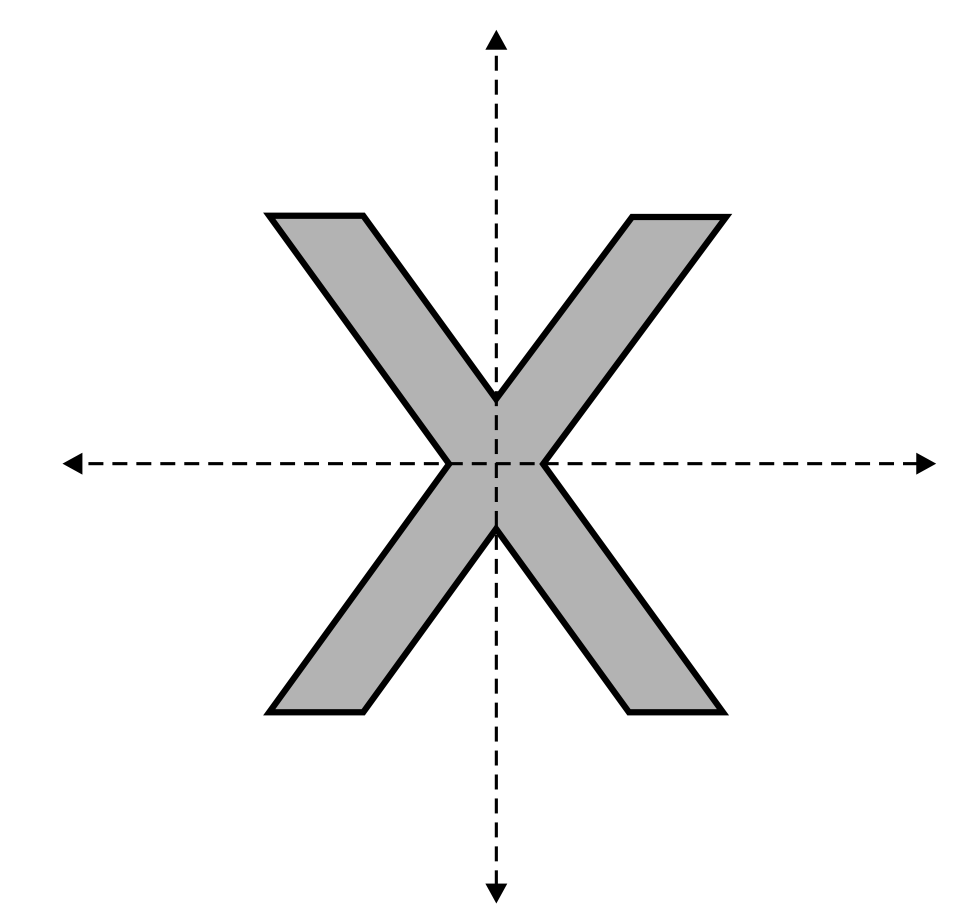
Which letter has exactly two lines of symmetry?
The letter X has a vertical line of symmetry and a horizontal line of symmetry. When an imaginary line passes through the center of the letter X horizontally and vertically, it creates identical halves. The other answer options have no lines of symmetry.
Which image shows a dotted line that is not a line of symmetry?
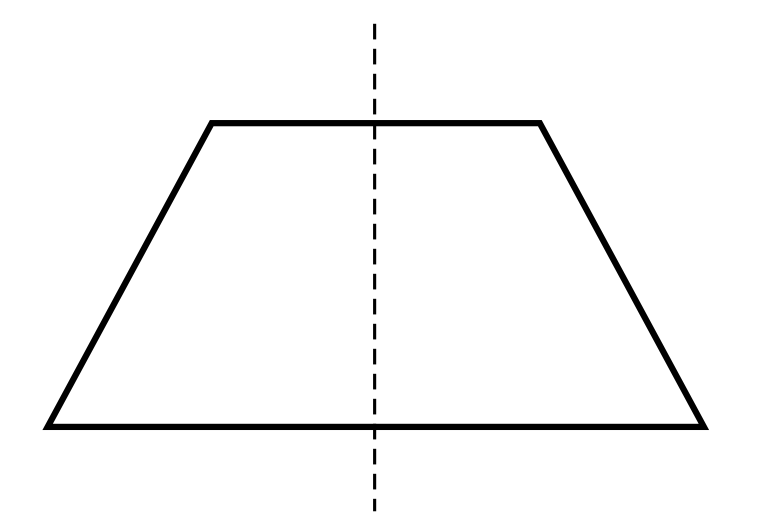
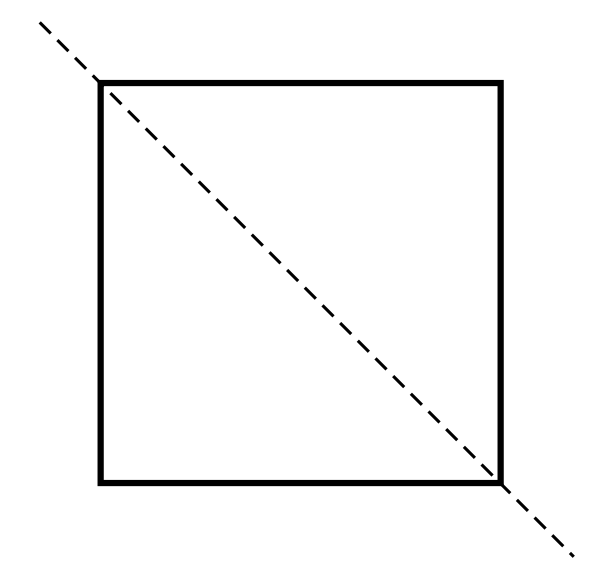
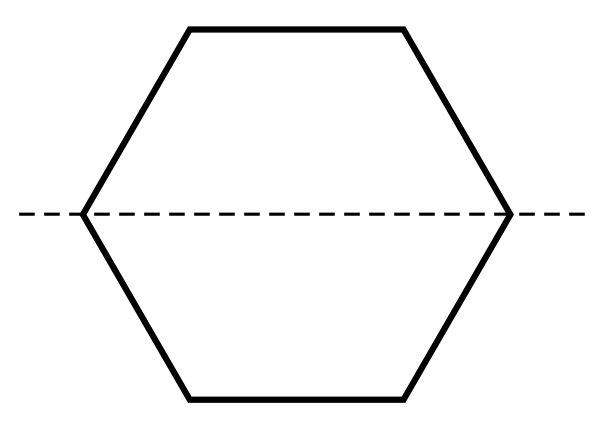
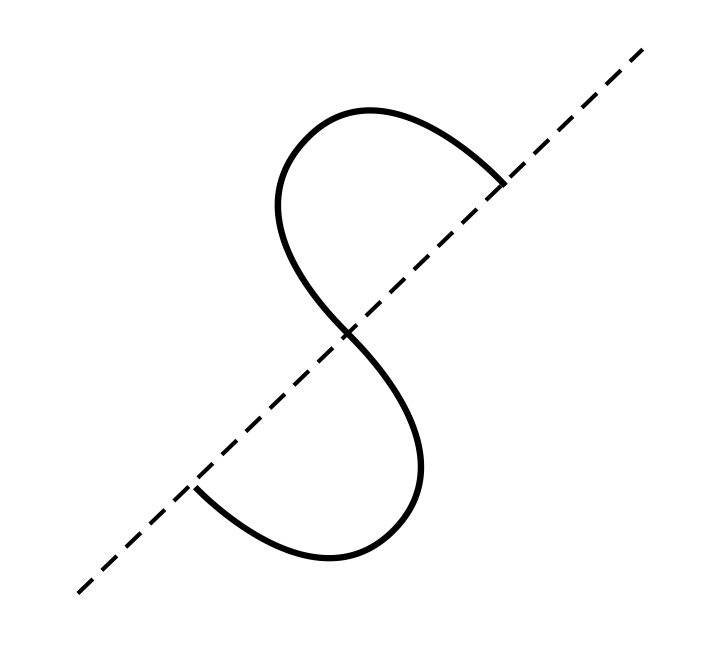
A line of symmetry splits a shape in half, creating two identical shapes. The two halves of the S shown are not identical. Therefore, the dotted line in Choice D is not a line of symmetry.
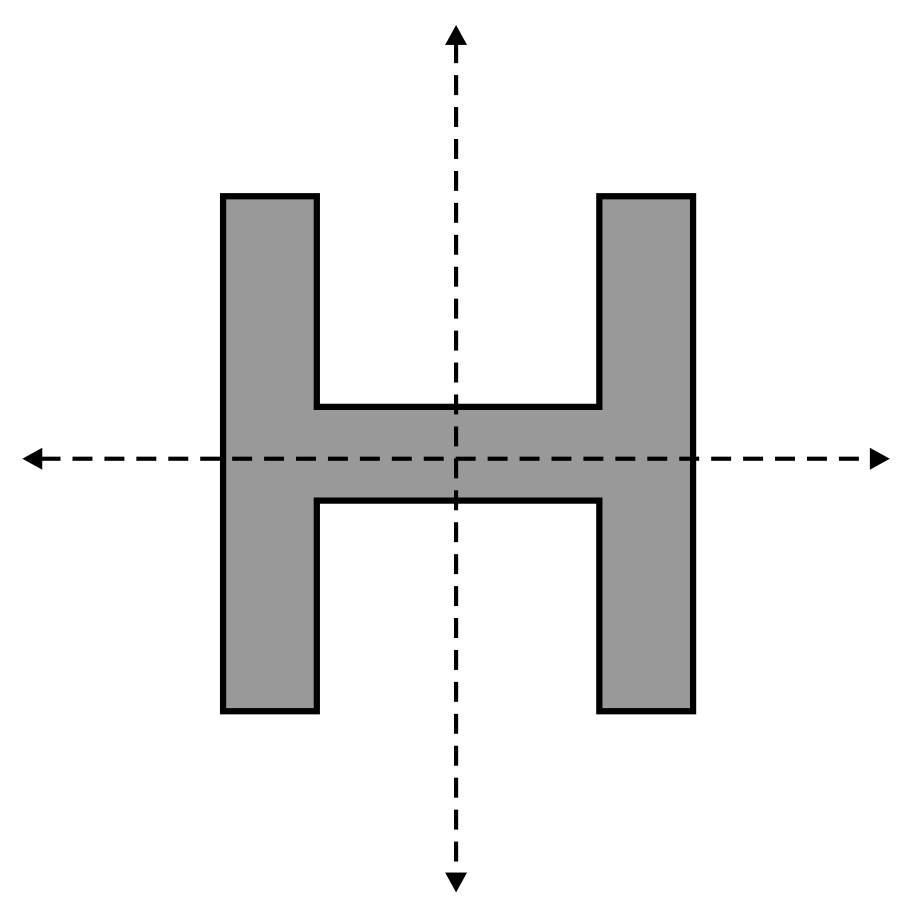
Kate is a graphic designer and is creating a logo with the letter H. She needs to identify its lines of symmetry so she can arrange the logo with precision. How many lines of symmetry are in the letter H?
The letter H contains two lines of symmetry: a vertical and a horizontal line of symmetry.
Juan is learning about symmetry in his math class. For homework, his teacher tells the class to find examples of objects that have a point of symmetry. The next day in class, Juan says he found four objects with a point of symmetry: the letter A, a King of Hearts playing card, an hourglass, and a plate. His teacher tells him that all his objects have a point of symmetry except for one. Which of Juan’s objects does not have a point of symmetry?
Point symmetry occurs when every part of an image has a matching part that is the same distance from the central point but in the opposite direction. The letter A does not have an origin point that divides the figure to create two matching parts in opposite directions. The rest of the objects listed do have point symmetry.