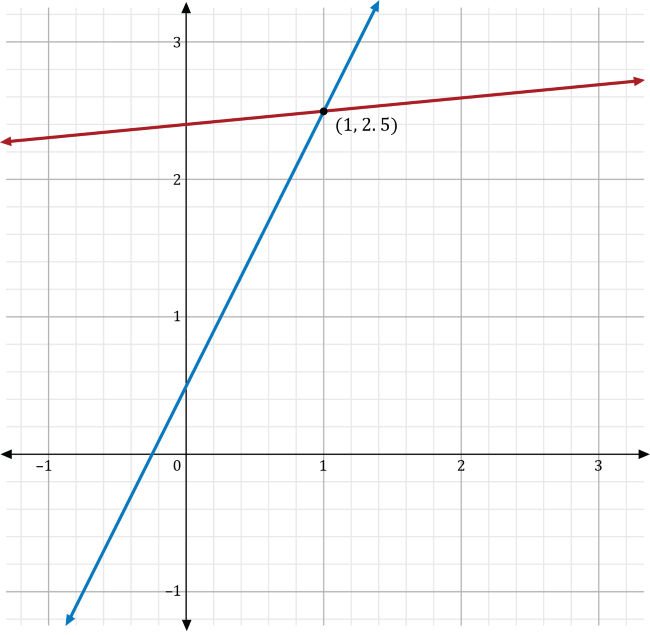Mometrix’s Algebra I videos are general reviews of the concepts, ideas, and topics that may be presented on an exam. Each of these videos will give a wide-scope review of what a test taker may need to know as they prepare to take a test.
Algebra 1 Online Prep Course
If you want to be fully prepared, Mometrix offers an online Algebra 1 prep course designed to give you everything you need to succeed!
Here’s what you’ll find in the Algebra 1 course:
- 80 Review Lessons Covering Every Topic
- Over 1,600 Algebra 1 Practice Questions
- 50+ Review Videos
- Money-back Guarantee
- Mobile Access
Everyone learns differently, so we’ve tailored the Algebra 1 online prep course to ensure every learner has what they need to prepare for the Algebra 1 exam.
Click below to check it out!
Algebra Basics
Linear Equations
Manipulating Expressions
Ratios and Percentages
Inequalities
Quadratics
Functions
Systems of Equations and Their Solutions
Applications
Practice Question Videos
Algebra I Problems
Finding the Slope of a Line. What is the slope of a straight line that passes through the points \(\left(0,-3\right)\) and \(\left(4,5\right)\)?
Slope is defined as the steepness of a line and can be calculated using the formula “rise over run.” More precisely, this formula is equal to the change in \(y\)-value (“rise”) divided by the change in \(x\)-value (“run”) between two points. To find these changes in values, use \(y_2-y_1\) and \(x_2-x_1\), where \(\left(x_1,y_1\right)\) and \(\left(x_2,y_2\right)\) are points on the line.
\(m=\frac{\text{rise}}{\text{run}}=\frac{y_2-y_1}{x_2-x_1}\)
In this case, let \(\left(x_1,\ y_1\right)=\left(0,-3\right)\) and \(\left(x_2,y_2\right)=\left(4,5\right)\). Plug each value into the slope formula and simplify.
\(m=\frac{5-\left(-3\right)}{4-0}=\frac{5+3}{4-0}=\frac{8}{4}=2\)
Therefore, the slope of this line is 2.
Slope-Intercept and Point-Slope Forms. Cheryl is a real estate agent and has determined that the prices, \(y\), of residential properties varies based upon their square footage, \(x\), such that each additional square foot adds $100 to the cost of the property. Using information from randomly selected homes in the area, Cheryl determines that the point-slope equation \(y-205{,}000=100\left(x-2{,}000\right)\) relates price to square footage. What is this equation when converted to slope-intercept form?
Equations written in slope-intercept form are in the format \(y=mx+b\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. In this situation, the cost per square foot is $100. Therefore, the slope \(m\) is equal to 100. This can already be seen in the point-slope equation.
\(y-y_1=\mathbf{m}\left(x-x_1\right)\)
\(y-205{,}000=\mathbf{100}\left(x-2{,}000\right)\)
The quickest way to determine \(b\)’s value is to rearrange the point-slope equation so that \(y\) is by itself on the left and like terms are combined on the right. Add 205,000 to both sides of the equation.
\(y=100\left(x-2{,}000\right)+205{,}000\)
Now, distribute the 100 to the \(x\) and the –2,000.
\(y=100x-200{,}000+205{,}000\)
Finally, combine like terms to see that \(b=5{,}000\).
\(y=100x+5{,}000\)
This equation is now in slope-intercept form. From it we can quickly determine that the price of each property is equal to the square-footage times $100, plus a fixed cost of $5,000.
Adding and Subtracting Exponents. Simplify the following expression by combining like terms:
\(6x+2x^3-5x^2-3x^2+x^3-5x\)
To simplify, combine like terms with \(x\)’s and \(y\)’s and the same exponent. In those problems, you can only combine terms that have the exact same variable.
This expression has several terms with the variable \(x\), although to varying powers. Look for terms that have the same power of \(x\) and group them.
The highest power in this expression is \(x^3\), and there are two terms which have it: \(2x^3\) and \(x^3\). These may be combined to obtain \(3x^3\).
\(6x+\mathbf{2}\mathbf{x}^\mathbf{3}-5x^2-3x^2+\mathbf{x}^\mathbf{3}-5x\)
\(3x^3\ldots\)
The next power to look for is \(x^2\), which is seen in the terms \(-5x^2\) and \(-3x^2\). These terms combine to form \(-8x^2\).
\(6x+2x^3-\mathbf{5}\mathbf{x}^\mathbf{2}-\mathbf{3}\mathbf{x}^\mathbf{2}+x^3-5x\)
\(3x^3-8x^2\ldots\)
Finally, the remaining terms both have \(x\) to the first power. 6x and -5x combine to make \(x\).
\(\mathbf{6}\mathbf{x}+2x^3-5x^2-3x^2+x^3-\mathbf{5}\mathbf{x}\)
\(3x^3-8x^2+x\)
Solving Equations Involving Roots. Solve for \(x\) in the equation \(\sqrt{x+10}-4=2\).
To get \(x\) by itself, first move –4 to the other side of the equation by adding 4 to both sides.
\(\sqrt{x+10}=2+4\)
\(\sqrt{x+10}=6\)
The next step is getting rid of the square root symbol. A square root can be undone by squaring it. Square both sides of the equation.
\(\left(\sqrt{x+10}\right)^2=\left(6\right)^2\)
\(x+10=36\)
Subtract 10 from both sides.
\(x=26\)
When working with roots, it is always important to check for extraneous solutions. Do this by substituting \(x=26\) into the original equation and checking to see if the statement is true or not.
\(\sqrt{\left(26\right)+10}-4=2\)
\(\sqrt{36}-4=2\)
\(6-4=2\)
\(2=2\)
Since \(2=2\) is a correct statement, \(x=26\) is a solution to the equation.
Percent Change. Michael observed that one summer day, his aunt’s snow-cone stand sold 80 snow-cones. The next day was hotter than the first, and 92 snow-cones were sold. By what percentage did sales increase from the first day to the second?
The percent change from one observation to the next can be found using the formula \(\text{percent change}=\frac{\text{new}-\text{old}}{\text{old}}\times100\%\). The numerator, \(\text{new}-\text{old}\), represents the change, or difference, in the observations. A positive amount means that there is an increase, while a negative amount indicates a decrease. In this scenario, the new amount is 92 and the old amount is 80. From this it can be seen that there was an increase of 12 sno-cones.
\(\frac{\text{new}-\text{old}}{\text{old}}\times100\%\)
\(=\frac{92-80}{\text{old}}\times100\%\)
\(=\frac{12}{\text{old}}\times100\%\)
This amount is divided by the old amount, 80, to determine the ratio of the change to the original amount. Here, \(\frac{12}{80}\) reduces to \(\frac{3}{20}\), or equivalently 0.15.
\(=\frac{12}{\text{old}}\times100\%\)
\(=\frac{12}{80}\times100\%\)
\(=0.15\times100\%\)
The final step in using the percent change formula is multiplying by 100 to convert from a decimal to a percentage. Here, \(0.15\times100=15\%\).
\(0.15\times100\%=15\)
Solving Multi-Step Inequalities. If Sheila’s Candle Co. sells premium homemade candles for $8.00 each and there is an annual fixed production cost of $352, at least how many candles must be sold each year to break even? Let \(x\) represent the number of candles sold in the net-profit inequality \(8x-352\geq0\). (Solve for \(x\) to determine the number of candles that must be sold to break even.)
The expression \(8x−352\) represents net income, and the inequality that sets it greater than or equal to zero restricts the value of \(x\) (candles sold) so that net income is not negative. To determine at least how many candles are required to break even, solve for \(x\). This process is nearly identical to solving for \(x\) when there is an equals sign rather than an inequality sign.
First, add 352 to both sides.
\(8x−352+352≥0+352\)
\(8x≥352\)
Now, divide both sides by 8 to get \(x\) by itself.
\(\frac{8x}{8}≥\frac{352}{8}\)
\(x≥44\)
This means that Sheila’s Candle Co. has a net profit of zero dollars or greater when 44 candles are sold.
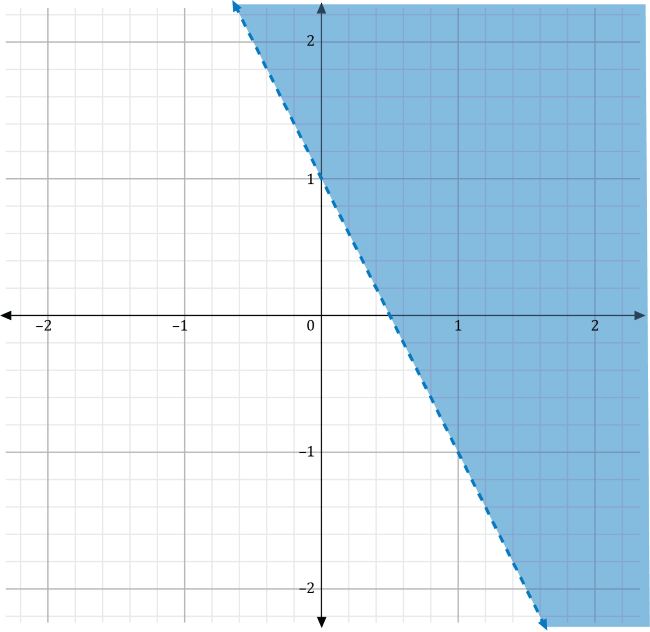
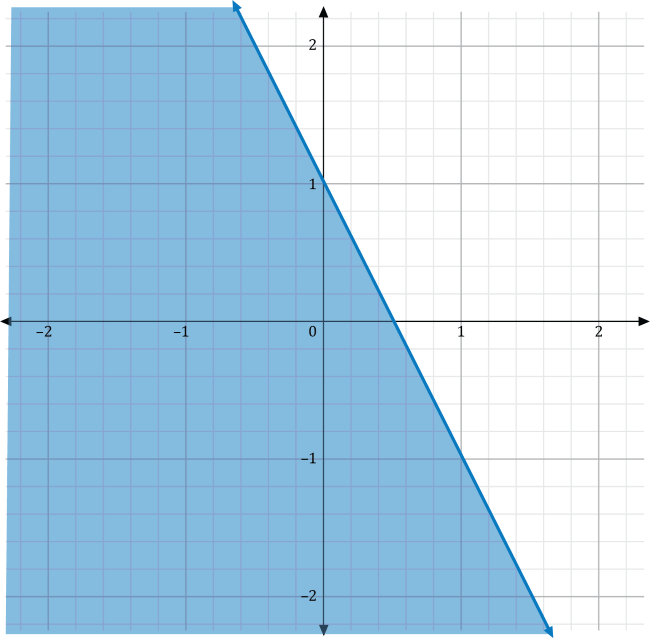
Graphing Linear Inequalities. Which of the following graphs represents the inequality \(y>-2x+1\)?
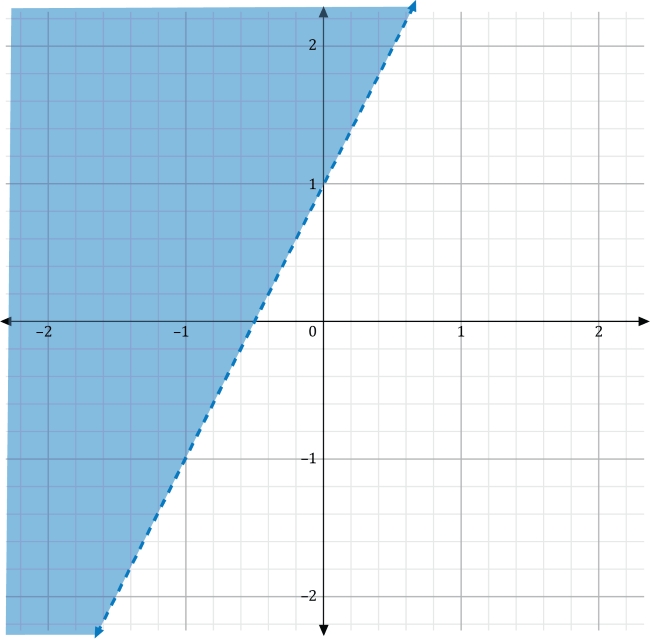
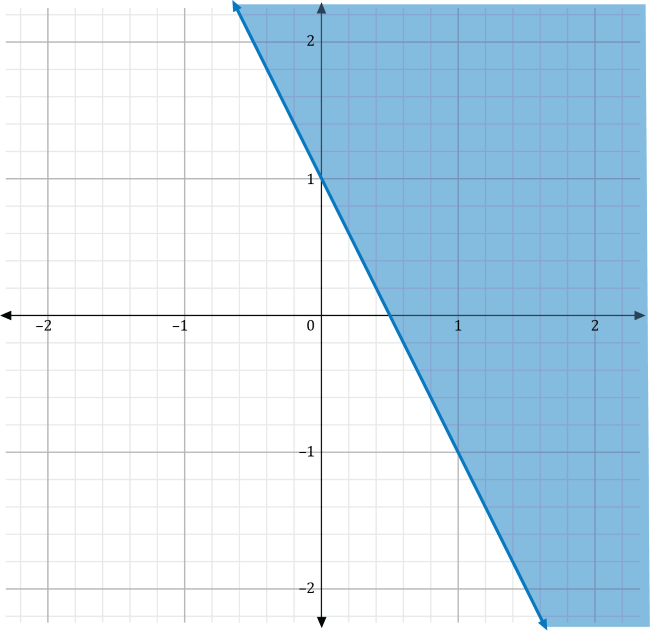
When graphing linear inequalities, a helpful first step is drawing the line on the graph. In this case, the line is \(y=-2x+1\). It has a slope of –2 and a \(y\)-intercept at 1. To plot this, mark the \(y\)-intercept at the point \(\left(0,1\right)\), and then use the slope, \(\frac{-2}{1}\), to mark another point that is down two spaces and to the right one space. This will go to the point \(\left(1,-1\right)\).
Notice that the inequality \(y>-2x+1\) has a greater-than sign rather than a greater-than-or-equal-to sign. Because of this, the line drawn on the graph will be a dashed line. Use a dashed line to connect the points \(\left(0,1\right)\) and \(\left(1,-1\right)\).
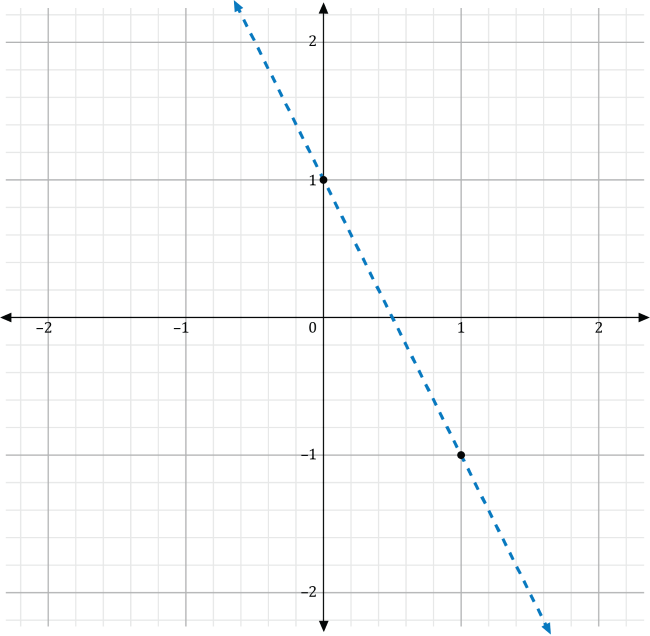
The final step in plotting this inequality is denoting whether the appropriate area lies above or below this dashed line. A quick way to make this determination is by noting that since the greater-than symbol \((>)\) is used, the area is greater than, or above, the line.

This step may be checked by plugging the point \(\left(0,0\right)\) into the inequality and seeing whether it is included in the shaded area.
\(y>-2x+1\)
\(0>-2\left(0\right)+1\)
\(0>0+1\)
\(0>1\)
Zero is not larger than 1. This informs us that the point \(\left(0,0\right)\) is not included in the shaded region. Since \(\left(0,0\right)\) is below the dashed line, we would instead shade the area that is above the dashed line.
Adding and Subtracting Polynomials. Shaun’s father works as a sales analyst for a car manufacturing company and determines that the monthly profits in U.S. dollars from Model A and from Model B can be estimated using the following functions, where x represents the number of vehicles produced that month.
\(A\left(x\right)=-x^2+400x-20{,}000\)
\(B\left(x\right)=-x^2+600x-65{,}000\)
Determine how much profit is generated by the manufacturing company from both models by adding together \(A\left(x\right)\) and \(B\left(x\right)\).
To add together \(A\left(x\right)\) and \(B\left(x\right)\), write out their equations with a plus sign between them.
\(A\left(x\right)+B\left(x\right)=\left(-x^2+400x-20{,}000\right)+\left(-x^2+600x-65{,}000\right)\)
Since this situation deals with addition rather than subtraction, the parentheses may be dropped.
\(-x^2+400x-20{,}000-x^2+600x-65{,}000\)
The next step is to combine like terms based on their powers of \(x\). Combine like terms to find the profit function for Models A and B.
\(-2x^2+1{,}000x-85{,}000\)
Vertex of a Parabola. Which of the following functions has a vertex at the point \(\left(-1,3\right)\)?
Each of the four functions shown are written in vertex form.
\(f\left(x\right)=a\left(x-h\right)^2+k\)
In vertex form, h and k are the x- and y-coordinates of the vertex, respectively. That is, \(\left(h,k\right)\) is the vertex. The variable a denotes a coefficient.
Because we want a vertex at the point \(\left(-1,3\right)\), let \(h=-1\) and \(k=3\). Plug these values into vertex form.
\(f\left(x\right)=a\left(x-\left(-1\right)\right)^2+3\)
Now, simplify.
\(f\left(x\right)=a\left(x+1\right)^2+3\)
Since a is a coefficient, it can be any number. Out of the four options given, only one follows this structure, choice B: \(f\left(x\right)=-2\left(x+1\right)^2+3\).
Choice A is not correct because its vertex is at the point \(\left(1,3\right)\). Choice C is not correct because its vertex is at \(\left(1,0\right)\). Choice D is not correct because its vertex is at \(\left(3,-1\right)\).
Solving Systems of Equations. Over the course of one week, Trina kept track of the heights of some plants in her garden, including a tomato plant and a bamboo shoot. The tomato plant started out taller than the bamboo shoot but grows slower than bamboo does. The system of equations below represents the growth of the two plants. After how many days \(x\) will the two plants have the same height, and what is that height \(y\), in feet?
\(\begin{cases}
x-10y=-24 \\
4x-2y=-1
\end{cases}\)
Systems of equations can be solved using either substitution or elimination. Since these equations do not have a common \(x\)-coefficient or \(y\)-coeffient, it will likely be quicker to use substitution.
The first equation can be solved for \(x\) by moving the \(y\)-term to the other side.
\(x-10y=-24\)
\(x=-24+10y\)
Now that we know that \(x=-24+10y\), plug this value into the second equation in place of \(x\).
\(4x-2y=-1\)
\(4\left(-24+10y\right)-2y=-1\)
Simplify by distributing and combining like terms.
\(-96+40y-2y=-1\)
\(-96+38y=-1\)
Solve for \(y\).
\(38y=95\)
\(y=\frac{95}{38}=2.5\)
We now know that the solution to the system of equations has a \(y\)-value of 2.5. Use this information to determine the \(x\)-value of the solution. Since \(x=-24+10y\) and \(y=2.5\), substitute 2.5 for \(y\) and solve for \(x\).
\(x=-24+10\left(2.5\right)\)
\(x=-24+25\)
\(x=1\)
This indicates that after one day, the bamboo catches up to the tomato plant at a height of 2.5 feet. The system of equations can also be graphed using two lines, as shown below. The point at which the two lines intersect is the solution to the system.