Multiplying Polynomials

Hey guys, today I’m going to walk you through a few different ways to multiply polynomials.

First, we’re going to take a look at multiplying binomials by each other.

So, a binomial might be something like $(4x+3)(-2x+1)$. This is an example of multiplying binomials by each other. And then we’re going to take a look at multiplying a binomial (so again, something like, $-2x-7$) times a trinomial, which would be like, $3x^2+4x-9$.

So even though we’re only working through these two types of problems, the steps we’re going to use will work for even larger polynomials.

Multiplying Binomials

To multiply polynomials, you need to multiply each part of the first polynomial by each part of the second polynomial, which, if we draw arrows to show that, looks like this:

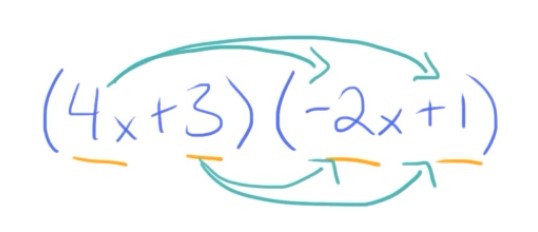
This can sometimes be a little tricky to keep track of, so it’s really important to make sure you have a system of how to solve these problems so you don’t miss any steps. The first way I’m going to show you how to multiply polynomials is by using the box method.

Example #1: Box Method

Let’s use the box method to multiply $(2x+5)(-4x+7)$.

Okay, so the first thing to notice is that we’re multiplying two binomials, like we talked about earlier, so we are going to want to set up a $2\times 2$ box. That’ll look like this:

We’re going to write one polynomial on the left and one on the top, like this:

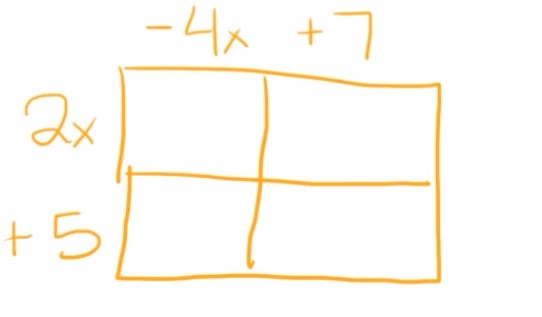
Since we are multiplying, it doesn’t matter which binomial goes on top and which one goes on the left.

Now we are going to multiply our left term by our top term for each box.

I’m going to start here with $2x\cdot (-4x)$, which will give us $-8x^2$. Then we’re going to move on to our next box where we multiply our left term by our top term. So $2x\cdot 7=14x$. Down here we have, $5\cdot (-4x)=-20x$. And then we’ll have, $5\cdot 7=35$.

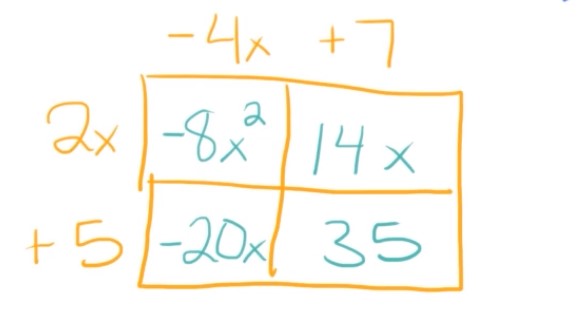
Okay, so now all our boxes are filled out and we can simply add our terms together.

 
Finally, all we have to do is combine our like terms to get our final answer. -20x and 14x are the only ones that are like terms, so we’ll have:

 
So that’s the box method.

Example #2: FOIL Method

The next way we’re going to use to multiply binomials is called the FOIL method.

We’re going to use the FOIL method to multiply: $(-3x-4)(6x+5)$.

Okay, so let’s take a look at what I just said for FOIL. FOIL stands for first (which means we’re going to multiply our first terms by each other), outer (which means we’re going to multiply our outer terms by one another), inner (which means we’re going to multiply our inner terms by one another), and finally, last (which means we’re going to multiply these last terms by each other). So, let’s do just that.

Let’s multiply our first terms together: $-3x\cdot 6x=-18x^2$. Then, multiply the outer terms: $-3x\cdot 5=-15x$. Next, multiply the inner terms: $-4\cdot 6x=-24x$. Finally, multiply the last terms: $-4\cdot 5=-20$. So now, all we have to do is add these terms together.

 
And the last thing we need to do is, again, combine our like terms. So $-15x$ and $-24x$ are like terms.

 
Now that we’ve taken a look at how to multiply binomials by one another, now we’re going to look at an example of multiplying a binomial by a trinomial using the box method again.

Multiply $(2x-3)(6x^2+4x+9)$.

Since we are working with a binomial and a trinomial, we are going to need to set up a $3\times 2$ box. So this one’s going to be a little bit longer than our last one. We’re still going to put 2 on the left side, and then we’ll put 3 on the top. So since we have our binomial multiplied by a trinomial, and we have a 2- and 3-side box, we’re going to need to put the binomial on the left.

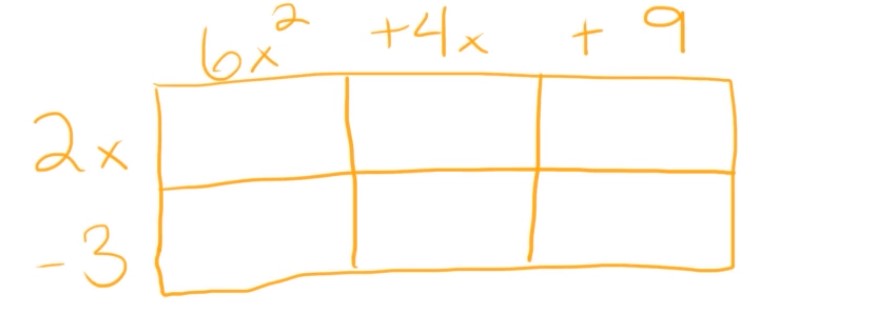
And now we’re going to multiply each box, just like we did last time. So I’m going to multiply, $2x\cdot 6x^2$, which is $12x^3$. Then we’ll go to, $-3\cdot 6x^2$, which equals $-18x^2$. Then I’m going to do, $2x\cdot 4x$, which is $8x^2$. $-3\cdot 4x=-12x$, $2x\cdot 9=18x$, and $-3\cdot 9=-27$.

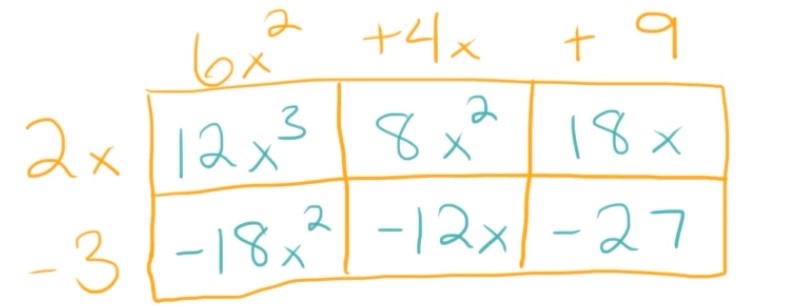
Now we’re going to add all of our terms together.

 
And finally, combine like terms. So, for this problem, we have like terms with $-18x^2$ and $8x^2$ and with $-12x$ and $18x$.

 
Using a box is just a tool for multiplying polynomials in a systematic way. Remember, at the beginning of this video, I said that you need to multiply each part of the first polynomial by each part of the second polynomial, which is what we did with our boxes.

Example #3

Now let’s walk through an example where we do this same thing but without using the box method.

Multiply $(6x-4)(-4x^2+8x-1)$.

Remember, you have to multiply each part of the first binomial by each part of the second trinomial. So technically, we can do this in any order, but to make sure that we do that, I’m going to show you a process that will help you not miss multiplying by terms.

I’m going to start by multiplying the first part of my first polynomial by each part of my second polynomial, and then add those terms together.

So, I’m going to start by multiplying the first part of my first polynomial by each part of my second polynomial. So just like I drew arrows right here.

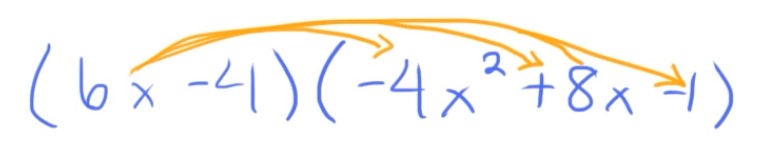
So I’m going to multiply $6x\cdot (-4x^2)$, that’ll give me $-24x^3$. Then I’m going to multiply $6x\cdot 8x$, which gives me $48x^2$. Then I’m going to multiply $6x\cdot (-1)$, which is $-6x$.

 
So from here, we’re going to multiply the second part of our binomial by each part of our trinomial, like this.

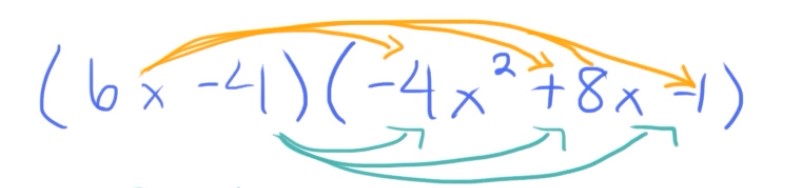
So same process, just with the second number. So I’m going to multiply $-4(-4x^2)$, which is $+16x^2$. Then I’m going to do $-4\cdot 8x$, which is $-32x$. And finally, I’m going to do $-4\cdot (-1)$, which is $+4$.

 
Now, all we have to do is combine like terms. So for this, our like terms aren’t right next to each other, so be careful in identifying which ones are which. $48x^2$ and $16x^2$ are like terms and $-6x$ and $-32x$ are like terms.

 
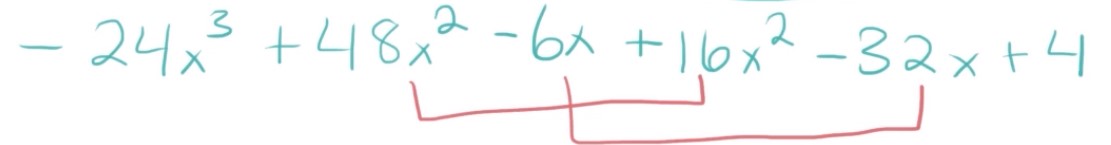
And that’s all there is to it! You can even use these steps to multiply two trinomials together, or even polynomials with 4 or 5 terms together. Just remember, you need to have a system for multiplying your terms together, because the larger your polynomials get, the easier it will be to accidentally miss multiplying some terms.

I hope this video on multiplying polynomials was helpful. Thanks for watching, and happy studying!