Dependent and Independent Variables with Inverting Functions
This video explains the differences between dependent and independent variables and inverting functions.

Hey guys! Today we’re going to take a look at independent and dependent variables, and then dive into the process of inverting functions.
Let’s step back and do a quick review of functions before we begin. Remember that a function relates inputs (x) and outputs (y). The output value will always depend on what you input. For a relationship to be a function, each input must have exactly one output.
| x (input) | y (output) |
| 0 | 3 |
| 1 | 6 |
| 2 | 9 |
| 3 | 12 |
We refer to these input and output values as either independent or dependent variables. We can plug in any value for x, so it is our independent variable. The y variable, however, will always depend on what was plugged in for x. So, we refer to the y variable as the dependent variable.
Let’s look at the function f(x) = 2x + 4 as an example. This equation is written in what’s called functional notation. f(x) essentially represents “y”, just as it would in the linear equation y = 2x + 4. f(x) is simply stating that the “y” value is “a function of x”, meaning that the “y” value will depend on what the “x” value is.
This particular function could reflect a scenario where x represents how many plants you sell at a farmers market, and f(x), or “y”, is how much money you will make. If you started with $4, and you sell each plant for $2, the money you earn (y) will depend on how many plants you sell (x). So in this scenario, the number of plants you sell is the independent variable, and the amount of money you make is the dependent variable. This makes sense because the amount of money you make should depend on how many plants you sell.
We can use this function to solve for y in terms of x. This means that we can choose any value for x, and use it to find the value of y.
For example, let’s say we started with the $4, and then we sell 26 plants at the farmers market. This means that x is equal to 26. Let’s plug 26 in for “x”, and then solve for y in terms of x to find out how much money we will make.
f(x) = 2x + 4
f(26) = 2(26) + 4
Now with a bit of algebra we can simplify the right side of the equation. 2 times 26 is 52, and then we add 4. This leaves us with f(26) = 56. We have solved for y in terms of x, or solved for y by plugging in a value for x. We can see that when x is equal to 26, y will be 56. So if we sell 26 plants at the farmers market at the end of the day we will have $56.
With this understanding of independent and dependent variables, we’re prepared to dive into the process of inverting functions.
Up to this point we have used examples of functions where we solve for “y” in terms of “x”.
Now let’s move on to the process of solving the inverse of a function. Finding the inverse of a function is essentially switching the input and the output. This means we are no longer using “x” to find “y”. We will now be using “y” to find “x”.
Let’s take it step by step to find the inverse of the function f(x) = 3x – 4.
Since we’re looking to find the inverse, we’ll need to write it like this: \(f^{-1} (x)=?\)
Finding the inverse of a function will be a 4-step process.
Step 1 is to write the function as a linear equation. So in this case we will write
f(x) = 3x – 4 as y = 3x – 4. Because we are switching the input and the output, we want to be working with x and y, instead of x and f(x). This will make the switch easier to see visually.
Step 2 is to simply swap x and y. This inverts the scenario from x being the input, to now y being the input.
Now the function should look like this: x equals 3y minus 4y.
\(y=3x-4\)
\(x=3y-4\)
Step 3 is simply to solve for y. To do that, let’s use inverse operations to isolate the variable. We’ll add 4 to both sides, and then divide by 3. X equals 3y minus 4, now becomes y equals x plus 4 over 3.
x = 3y – 4 now becomes y = x + 43
Our last step, Step 4, is to write the equation in inverse notation. So f inverse of x is equal to x plus 4 over 3.
\(f^{-1} (x)=\frac{x+4}{3}\)And there you have it! The inverse of the function f(x) = 3x – 4 is f -1(x)= x + 43.
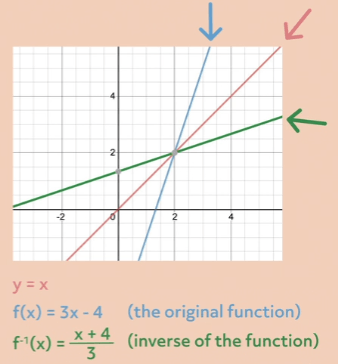
It is important to note that when you graph a function and its inverse on the same coordinate grid, an important relationship should be visible. You should notice that the two lines are reflected over the line y=x. So essentially, when you’re finding the inverse of a function, you are simply reflecting that function over the line y=x. Let’s graph the function and its inverse from the previous example so we can see this relationship.
f(x) = 3x – 4 (the original function)
f -1(x) = x + 43 (inverse of the function)
In our graph we can see the red line representing the line y=x. The blue line represents our original function, and the green line is the inverse of that function. When we graph the function and its inverse we are able to see visually that the lines are reflected over the red line y=x.
That’s all there is to it! I hope this review was helpful. Thanks for watching, and happy studying!
Dependent and Independent Variables with Inverting Function Practice Questions
Which set of values represents one set of output for the function \(f(x)=-3x+2\)?
The output is the result of substituting an input for x and evaluating. The resulting evaluation is the output of the function. The best way to see the output is by graphing the function, which will show that 5, 2, -1, and -4 are the outputs for the inputs -1, 0, 1, and 2, respectively. In other words, if you plug in -1, 0, 1, and 2 into the function for x, you will get 5, 2, -1, and -4.
The graph of function \(g(x)\) and its inverse, \(g^{-1}(x)\), are reflected over which line?
When a function and its inverse are graphed, it is possible to see that the graph of the inverse is reflected over the line \(y=x\).
The function \(t(x)=5x–15\), where x is the number of crates of eggs, represents Kian’s total daily income from selling crates of eggs at the Farmer’s Market. What is Kian’s income if he sells 28 crates of eggs in one day?
Since the function represents Kian’s income and the input, x, represents the number or crates of eggs, we can substitute 28 for x and evaluate to find Kian’s daily income at the Farmer’s Market.
\(t(x)=5x–15\)
\(t(x)=5(28)–15\)
\(t(x)=140–15\)
\(t(x)=125\)
Therefore, Kian’s daily income for selling 28 crates of eggs is $125.
Which shows the inverse of function \(f(x)=\frac{1}{2}x-3\)?
To find the inverse of a function, we use the following steps. First, we replace the function notation with y. Next, we switch the x and y and solve for y.
\(f(x)=\frac{1}{2}x-3\)
\(y=\frac{1}{2}x-3\)
\(x=\frac{1}{2}y-3\)
\(x+3=\frac{1}{2}y\)
\(2(x+3=\frac{1}{2}y)\)
\(2x+6=y\)
\(f^{-1}(x)=2x+6\)
Nadya uses the function of \(I(x)=0.05x+20\) to calculate her monthly car insurance, where x represents the number of miles, she drives each month. How much is her July bill if she drives 45 miles?
We can find Nadya’s July car insurance bill by substituting 45 for x and evaluating.
\(I(x)=0.05x+20\)
\(I(x)=0.05(45)+20\)
\(I(x)=2.25+20\)
\(I(x)=22.25\)
Therefore, the total car insurance bill for driving 45 miles is $22.25.
