Solving One-Step Inequalities

Hello! Welcome to this video on solving one-step inequalities. This process should look very similar to the process of solving one-step equations.
Let’s jump into some examples!
\(x+7\gt -3\)
Since the goal, like with solving equations, is to isolate \(x\) on one side, we need to get rid of the \(+7\) on the left side. We do this by subtracting 7 from both sides, just like with a one-step equation.
\(x+7-7\gt -3-7\)
\(x\gt -10\)
And this is our answer for our inequality. Sometimes when you have one-step inequalities you’ll be asked to graph your solution. So if you were to graph this solution, it would look something like this:

Since we have a greater than sign, and not greater than or equal to, \(–10\) is not in the solution set. We show this with an open circle above \(–10\).
Let’s try another one! Solve the inequality:
\(x-\leq 23\)
To isolate \(x\) on the right side, add 2 to both sides.
\(x-2+2\leq 3+2\)
\(x\leq 5\)
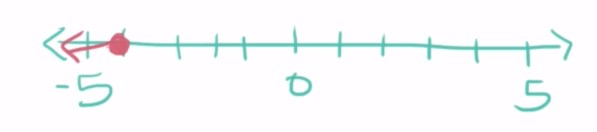
Now let’s draw a graph of our solution. Because there is a less than or equal to sign, 5 is included in our answer, and we use a closed dot on our graph.

Now let’s try an example where we have to use division.
\(-4x\geq 16\)
To isolate \(x\), we will have to divide both sides by \(–4\).
\(\frac{-4x}{-4}\geq \frac{16}{-4}\)
However, before we go forward, I need to tell you of one special rule. When we divide or multiply by a negative number with inequalities, we have to flip our inequality sign. If you don’t, your answer will be wrong. So here, our answer will be:
\(x\leq -4\)
It’s very important that you flip your inequality sign when multiplying or dividing by a negative number. Now let’s graph our answer. Since we have a less than or equal to sign again, we use a closed dot.
Let’s work through one more example together.
\(\frac{x}{6}\lt 1\)
To isolate \(x\), we need to multiply both sides by 6.
\(6\cdot \frac{x}{6}\leq 16\)
\(x\lt 6\)
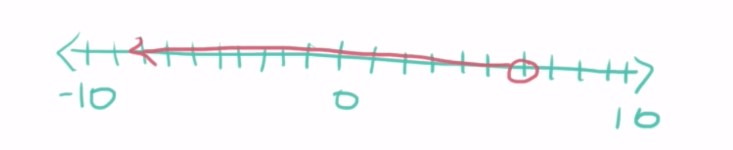
Because we multiplied by a positive number, we don’t have to flip our inequality sign. Then we can graph our solution. We’re gonna draw an open circle above 6 because we have a less than sign, 6 is not included in the solution set.
I hope this video on solving one-step inequalities was helpful. Thanks for watching, and happy studying!
