Scientific Notation

Hi, and welcome to this video about scientific notation! In this video, we will explore what scientific notation is and how to write and compare numbers in scientific notation.

First, what is scientific notation? The idea of scientific notation was developed by Archimedes in the 3rd century BC, where he outlined a system for calculating the number of grains of sand in the universe, which he found to be 1 followed by 63 zeroes. His work was based on place value, a novel concept at the time.

What is Scientific Notation?

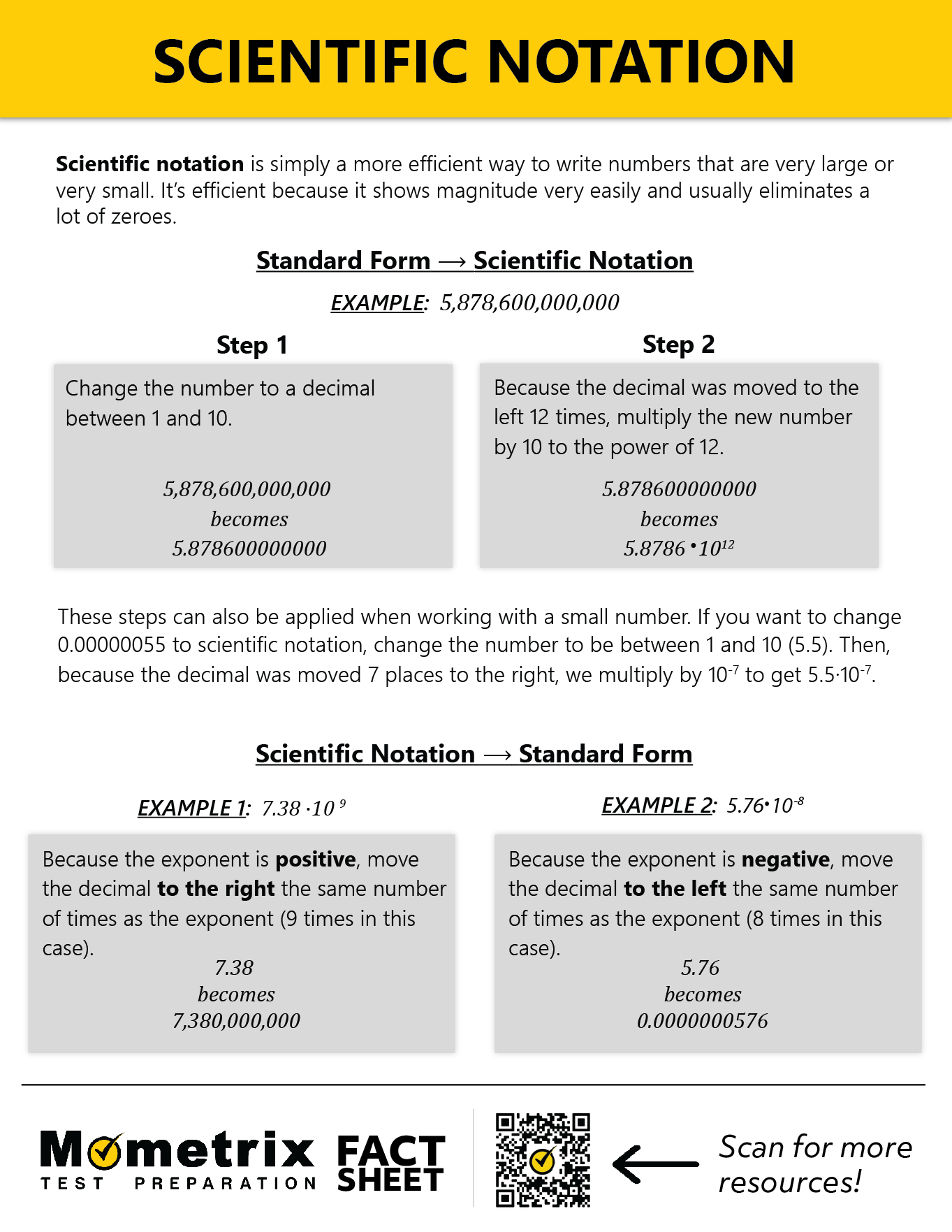
Scientific notation is simply a way of writing numbers. It is especially useful in expressing very large or very small numbers because it is shorter and more efficient and it shows magnitude very easily.

Every real number can be written as a product of two parts: a decimal part times an integer power of ten.

\(m \times 10^n\), where \(1\) ≤ \(m\) < \(10\) and \(n\) is an integer

Why 10? Our number system is based on 10, and each place value is 10 times the previous place value. One ten equals ten ones; one hundred equals ten tens, etc.

Let’s look at writing large numbers using this notation system:

We can write the number 1 as \(1 \times 10^0\). Remember, \(10^0=1\), so \(1 \times 1=1\).

We can also write the number 13 as \(1.3 \times 10^1\) because \(1.3 \times 10=13\).

We can write the number 134 as \(1.34 \times 10^2\) because \(1.34 \times 10 \times 10=134\).

Let’s look again at Archimedes’ findings. He expressed the number of grains of sand in the universe as “1 followed by 63 zeroes.” We could write that out, but that would take way too long and be highly inefficient.

In scientific notation, this would be \(1 \times 10^{63}\), a much more compact and efficient way of expressing this number. The number of zeros in the gigantic number is represented by the exponent. In the fully written number, it’s important to realize each time we multiply by 10, we move to a new place value. So adding a zero means multiplying by 10.

A light-year (the distance light travels in a year) is 5 trillion 878 billion 600 million miles. Let’s express this in scientific notation. Often, this is described as “moving the decimal point,” which doesn’t actually happen. We simply need to count the number of times we multiply by 10.

The decimal part is created from the first block that begins and ends with a non-zero number (in other words, the block can contain a 0, but we don’t use the zeros at the end).

\(5,878,600,000,000\)

Our decimal must be greater than or equal to 1 and less than 10. So we always start from the ones place. Here, we have:

\(5.8786×10^?\)

This is where we count the number of times our decimal is multiplied by 10. We need to count from the decimal we created to the end of the number:

\(5.876 \times 10^1=58.786\)
\(5.876 \times 10^2=587.86\)
\(5.876 \times 10^3=5,878.6\)
and so on and so on until we reach
\(5.876 \times 10^{12}\)\(=5,876,000,000,000\)

So, in scientific notation, a light-year can be expressed as \(5.876 \times 10^{12}\) miles.

But what if you wanted to take a number written using scientific notation and change it into standard form?

A light-year can also be expressed as \(9.4607 \times 10^{15}\) meters. We can easily change this number to standard form.

\(9,460,700,000,000,000\)

Start with the decimal part (9.4607) and multiply by 10 a total of 15 times. This tells us that a light-year is 9 quadrillion 460 trillion 700 billion meters.

Scientific Notation Examples

Let’s look at a couple more examples before we move on:

If I google “light year,” I’m given about 7 billion 380 million search results. Let’s express this number in scientific notation.

\(7,380,000,000\)
\(7.380000000\)
There are nine digits after the decimal, so our exponent will be 9.
\(7.38 \times 10^9\)

As you can see, I was given \(7.38 \times 10^9\) search results.

On average, there are \(3.72 \times 10^{13}\) cells in a human body. Express this number in standard form.

The exponent 13 tells us that we have thirteen numbers after the decimal, which gives us 3.72 followed by 11 zeros. If we multiply this by ten 13 times, we see that there are 37.2 trillion cells in the human body.

So now we know how to write large numbers using scientific notation, but what about small numbers?

First, let’s recall how negative exponents work. For example:

\(10^{-1}\text{ }\)\(= \frac{1}{10^1}= \frac{1}{10}\)
\(10^{-2} \text{ }\)\(=\frac{1}{10^2}=\frac{1}{100}\)

Where positive exponents represent multiplication, negative exponents represent division.

The number 1 can be written as \(1 \times 10^0=1 \times 1=1\).
The number 0.1 can be written as \(1 \times 10^{-1}=1 \times \frac{1}{10}=0.1\).
The number 0.01 can be written as \(1 \times 10^{-2}=1 \times \frac{1}{100}=0.01\).

The wavelength of green light is 0.00000055 meters. Let’s see this in scientific notation.

We begin the same way as with large numbers—creating the decimal from the chunk bookended by non-zero numbers. Our result will resemble \(5.5 \times 10^{-?}\).

Now, we count the number of times our decimal is divided by 10.

\(5.5 \times 10^{-1}=.55\)
\(5.5 \times 10^{-2}=.055\)
\(5.5 \times 10^{-3}=.0055\)
and so on and so on until we reach
\(5.5 \times 10^{-7}=.00000055\)

So, in scientific notation, the wavelength of green light can be expressed as \(5.5 \times 10^{-7}\) meters.

The radius of a hydrogen atom is \(2.5 \times 10^{-11}\) meters. We can express this in standard form by starting with the decimal part 2.5 and dividing by 10 a total of 11 times.

This tells us that the radius of a hydrogen atom is 0.000000000025 meters.

I hope that this video helped you understand how to work with numbers in scientific notation!

Thanks for watching, and happy studying!

Frequently Asked Questions

How to do Scientific Notation PDF

Your How to do Scientific Notation PDF Download

Scientific Notation Practice Problems