Sometimes in math and science classes, you may see very large numbers, like this…
…or very small numbers like this:
In this video, we are going to talk about how to write and understand numbers just like these, and how to tell just how big or small they really are!
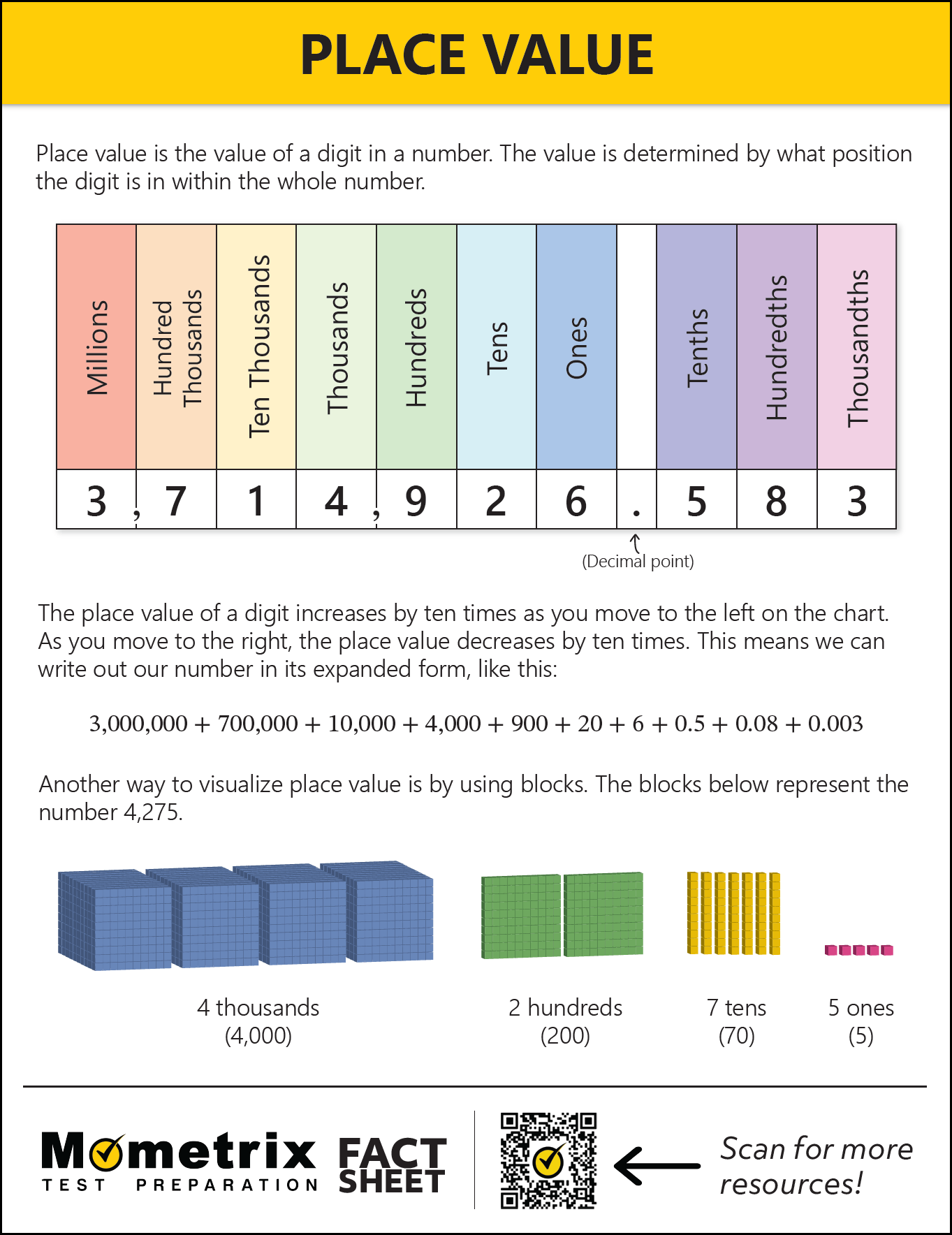
Understanding Place Value
Digits
To begin, let’s take a look at the number 125. This number is made up of three numbers put together: a 1, a 2, and a 5. Because there are three numbers, we say that 125 has three digits.
Similarly, the number 79 has two digits, because it is made up of two numbers, a 7 and a 9.
3,044 has four digits, because it has four numbers, a 3, a 0, and two 4s.
Ones Place
Let’s zoom out a little and think about how larger numbers are constructed. Take a look at the number 2,175. Each digit in this number has a name. The digit farthest to the right is called the ones place because the first number in math with one digit is 1. In this example, 5 is in the ones place.
Tens Place
Just to the left of the ones place is the tens place. The tens place is where the second digit goes, and we can remember this because the first number with two digits is 10. Here, 7 is in the tens place.
Hundreds Place
The third digit from the right is called the hundreds place, and that’s where we write a digit when we are talking about numbers 100 or larger! The number 1 in our example is in the hundreds place.
Thousands Place
The fourth digit from the right is called the thousands place, and that’s where we write a digit whenever we are talking about numbers 1,000 or larger. In this example, the number 2 is in the thousands place. For numbers that are 1,000 or larger, the digits can become a little trickier to read. To help organize the digits, we use commas after every third digit from the right. For numbers in the thousands, we place a comma after the thousands place!
Labeling Place Value – Smaller Numbers
Let’s take a moment now to label the digit places in the numbers 125, 79, and 3,044.
For the number 125, what place is the number 5 written in? Since 5 is the number farthest to the right, it is in the ones place, so we would say that the place value of 5 in 125 is five ones, or 5.
What place is the number 2 written in? Since 2 is the second number from the right, we see that it is in the tens place. So the place value of 2 in 125 is two tens, or 20.
What is the place value of 1 in 125? Since 1 is the third digit from the right, it is in the hundreds place and has a place value of 100.
What about the number 79? Which number is in the tens place? 7 is, because it is the second digit from the right. What place is the 9 in? The 9 is in the ones place.
Let’s check the number 3,044 now. What is the place value of the 3? Since 3 is the fourth digit from the right, and because it comes before the comma, it is in the thousands place, and its place value is 3 thousands. What number is in the hundreds place? Zero is, since it is the third digit from the right. And what about the fours? The first 4 is in the tens place, and the second 4 is in the ones place.
Labeling Place Value – Larger Numbers
As I mentioned in the beginning of this video, there are also names for digits much higher than the thousands place! Let’s take a look at a number with seven digits.
Ten-Thousands Place
We already know how to label the first four digits from the right as the ones place, tens place, hundreds place, and thousands place. What do we call the digit where 5 is at, though? This digit is called the ten-thousands place because the first five-digit number is 10,000.
Hundred-Thousands Place
Can you guess what the sixth digit is called? The sixth digit is called the hundred-thousands place.
Millions Place
And finally, the 1 in this number is the seventh digit from the right, and is followed by another comma. This signals to us that it is in the millions place!

Let’s do another example of labeling the place values of digits in a larger number.
For the number 3,571,068, which number is in the ten-thousands place? The ten-thousands place is just to the left of the thousands place, so 7 is in the ten-thousands place.
What is the place value of the number 0? Since 0 is the third digit from the right, it is in the hundreds place.
Which number is in the millions place? We know that the millions place comes just to the left of a comma and is the seventh digit from the right, so that means that 3 is in the millions place.
What is the place value of the number 5? The five comes just to the right of a comma, so we know that it is either the hundreds place or the hundred-thousands place. Because it is in the sixth digit from the right, it is in the hundred-thousands place and has a place value of 500,000.
What number is in the tens place? The tens place is the second digit from the right, so we see that 6 is in the tens place.
What is the place value of 1? Since 1 is the fourth digit from the right and is just to the left of a comma, we can tell that it is in the thousands place and has a place value of 1 thousand.
And finally, what number is in the ones place? 8 is, because it is the digit farthest to the right.
Expanded Form
Sometimes it can be helpful to rewrite a number in expanded form, where we write the number as the sum of each digit’s place value. For example, the number 125 can be written in expanded form as \(100+20+5\). Similarly, our three-million number can be written in expanded form as \(3,000,000+500,000+70,000\)\(+1,000+0+60+8\).
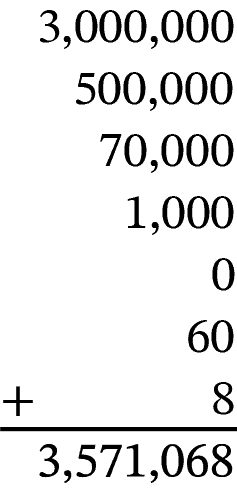
Labeling Place Value – Very Small Numbers
Now that we’ve covered the names of digits for very large numbers, we also need to talk about the names of digits for very small numbers. These very small numbers are written as digits following a period, or decimal point, after the ones place.
Tenths Place
For example, the number 1.5 is the same as \(1\frac{1}{2}\), but written in decimal form. The 1 is of course in the ones place, but the five is in a position called the tenths place. It’s called the tenths place because 0.1 is one-tenth of 1!
Numbers in decimal form can have more than one digit after the decimal, though. In fact, there could be dozens of digits after the decimal point! Usually, though, we are only concerned with the first few. As we just saw, the first digit to the right of the decimal point is called the tenths place.
Hundredths Place
The second digit after the decimal is called the hundredths place, because 0.01 is equal to one one-hundredth of 1.
Thousandths Place
And the third digit after the decimal is called the thousandths place. It is very important to include the “th” when talking about digit names after a decimal because the “th” distinguishes them from the digit name to the left of the decimal!
Let’s do one more example. Label the digits in the number 18.725.
We know that the first number, 1, is in the tens place and that the 8 is in the ones place, because these two numbers come before the decimal point. 7, 2, and 5 come after the decimal, so they are going to have positions in the tenths, hundredths, and thousandths places.
I hope you found this lesson helpful!
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is an example of place value?
A
Place value is a convenient way of separating the value of each digit in a number. An example of place value can be seen when working with money. For example, \($45.86\) consists of digits in the tens, ones, tenths, and hundredths place. When this value is split apart according to its place value, the amount becomes \($40+$5+$\frac{8}{10}+$\frac{6}{100}\). Place value is based on the base ten number system which is why digits increase or decrease by a factor of ten.
Q
What are tens and ones?
A
Tens and ones are represented by the first two digits to the left of the decimal point. For example, in the value \(94.0\), the \(4\) represents \(4\) groups of one \((4)\), and the \(9\) represents \(9\) groups of \(10\) \((90)\). When \(4\) ones and \(9\) tens are combined, the total value becomes \(90+4=94\).
Q
What is the ones place in a decimal?
A
The ones place is the digit that is directly to the left of the decimal point. For example, in the value \(3.4\), the digit \(3\) is in the ones place. In a number with no decimal point, the ones place is the digit farthest to the right. For example, in the value \(459\), the \(9\) is in the ones place because \(459\) is essentially \(459.0\).
Q
Why is there no oneths place?
A
There is not a “oneths” place because digits to the right of the decimal point become smaller by a factor of ten. This means that moving from the ones place to the tenths place is the result of dividing \(1\) by \(10\), which is one-tenth, not one-oneth.
Q
Which place is the tenths place?
A
In a decimal value, the first digit to the right of the decimal point is in the tenths place. For example, in the value \(34.592\), the digit \(5\) is in the tenths place. This \(5\) represents five tenths, or \(\frac{5}{10}\).
Q
What is the definition of a tenth?
A
A tenth represents the fraction “out of ten”. In a decimal value like \(3.4\), this means three ones, and \(4\) tenths. Another way to look at \(3.4\) is \(\frac{3}{1}+\frac{4}{10}\). The tenths place is always the digit directly to the right of the decimal point.
Q
Where is the tens place in a number?
A
The tens place is always located two digits to the left of the decimal point. Remember, even whole numbers can be written with a decimal point. For example, \(34\) can be written as \(34.0\), which means that \(3\) is in the tens place. This \(3\) represents \(3\) groups of ten. In the decimal value \(198.478\), the second digit to the left of the decimal is \(9\). This means that the \(9\) represents \(9\) groups of \(10\), or \(90\).
Q
How many tens make a thousand?
A
The base ten number system is convenient because all digits moving to the left become \(10\) times as large, and all digits moving to the right become \(10\) times smaller. This means that all place values can be compared by a factor of ten. For example, tens are \(10\) times as large as ones. Hundreds are \(10\) times as large as tens. Thousands are 10 times as large as hundreds. When making the jump from tens to thousands, we would need to multiply by \(10\) twice. So it would take \(100\) tens to make a thousand. For example, \(1{,}000\) is \(100\) times as large as \(10\).
What is Place Value? PDF
Number Place Value Practice Questions
What is 7,645 written in expanded form?
The correct answer is \(7,000+600+40+5\). To write a number in expanded form, write an addition problem that adds the value of each number. 7 is in the thousands place, so it represents 7,000. 6 is in the hundreds place, so it represents 600. 4 is in the tens place, so it represents 40. And 5 is in the ones place, so it represents 5. Added together this looks like: \(7,000+600+40+5\).
What is the place value of 9 in 293.76?
The correct answer is Tens. Place value names can be determined by their position in respect to the decimal point. The position to the left of the decimal point is the ones place. To the left of that is the tens place, and to the left of that is the hundreds place. The position to the right of the decimal point is the tenths place, and the one to the right of that is the hundredths place. Therefore, 9 is in the tens place.
What is 12,643.57 in expanded form?
The correct answer is \(10,000+2,000+600+\)\(40+3+\frac{5}{10}+\frac{7}{100}\). To write a number in expanded form, write an addition problem that adds the value of each number. 1 is in the ten-thousands place, so it represents 10,000. 2 is in the thousands place, so it represents 2,000. 6 is in the hundreds place, so it represents 600. 4 is in the tens place, so it represents 40. 3 is in the ones place, so it represents 3. 5 is in the tenths place, so it represents \(\frac{5}{10}\). And 7 is in the hundredths place, so it represents \(\frac{7}{100}\). Added together this looks like: \(10,000+2,000+600+\)\(40+3+\frac{5}{10}+\frac{7}{100}\)
What is the place value of 3 in 192.36?
The correct answer is Tenths. Place value names can be determined by their position in respect to the decimal point. The position to the left of the decimal point is the ones place. To the left of that is the tens place, and to the left of that is the hundreds place. The position to the right of the decimal point is the tenths place, and the one to the right of that is the hundredths place. Therefore, 3 is in the tenths place.
What is the place value of 6 in 162,497,132.498?
The correct answer is Ten-millions. The order of place value starting at the position left of the decimal and continuing to move left is: ones, tens, hundreds, thousands, ten-thousands, hundred-thousands, millions, ten-millions, and hundred-millions. Therefore, 6 is in the ten-millions place.